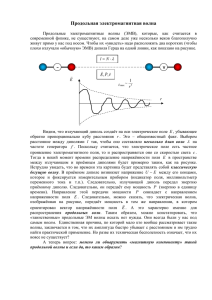
называется волной.

План лекции
1.Волны. Продольные и поперечные
волны
2.Скорость распространения волн
3.Характеристики звуковых волн
Волны. Продольные и поперечные волны.
Среда, частицы которой связаны между собой так,
что изменение положения одной из них ведёт к
изменению положения других частиц, называется
упругой.
Процесс распространения колебаний в упругой среде
называется волной.
При распространении волны частицы среды не
движутся вместе с волной, а колеблются около своих
положений равновесия.
В волне от частицы к частице передается лишь
состояние колебательного движения и энергия.
Основное свойство волны – перенос энергии без
переноса массы вещества.
Продольной называется волна, в которой частицы
колеблются вдоль направления распространения волны.
Такие волны могут распространяться в любой среде.
Если по концу свободно висящей пружины
ударить снизу вверх, то по пружине
пробежит волна, состоящая из сгущений и
разрежений.
Продольные и поперечные волны

v
T
2
k


k
v
Кратчайшее расстояние между центрами 2-х
ближайших сгущений или разрежений называется длиной волны ( λ ,[м] )
Поперечной - называется волна, у которой
частицы колеблются перпендикулярно направлению
распространения волны.
Поперечные
волны
могут
распространяться только в твёрдых
телах и на поверхности жидкости.
Если по свободному концу висящей
пружины ударить слева - направо, то
по
пружине
распространится
синусоида.
Волновая
поверхность-
геометрическое место точек,
колеблющихся в одинаковой
фазе.
Волновой фронт- геометрическое
место точек, до которых доходят
колебания к моменту времени t
- линия, перпендикулярная волновой
поверхности (эта линия показывает
направление распространения волны).
При переходе волны из одной
среды в другую.
-частота колебаний(ν) сохраняется
-скорость(V), длина волны (λ)
изменяются.
Скорость распространения волн
В жидкости и газе распространяются только продольные
волны. В твердых телах продольные могут существовать наряду
с поперечными.
В однородной среде волны распространяются равномерно,
поэтому скорость распространения волны можно определить по
формуле.

S

t
(1)
Если рассматривать движение волны за один период,
т.е t = T, то пройденное расстояние равно длине волны λ.


T
(2)
скорость распространения волны через период
1
Т.к T 
то

   
(3)
скорость распространения волны через частоту
E


Скорость распространения волны зависит от свойств
упругой среды, в которой волна распространяется.
где E - модуль Юнга среды, ρ-плотность среды.
Уравнение бегущей волны
Характеристики звуковых волн.
Звук представляет собой колебания упругой среды,
воспринимаемые
нашими
органами
слуха.
Человеческое ухо способно воспринимать колебания,
частота которых лежит в пределах от 16 до 20000 Гц.
Музыкальным тоном мы называем звук, которому
соответствует одна строго определенная частота.
Высота тона определяется частотой колебания, чем
больше частота, тем выше тон.
Звуки с различными частотами получили
название шумов.
Для характеристики звука целесообразнее ввести
энергетическую характеристику.
Интенсивностью звука -
называется величина
равная энергии переносимой звуковой волной в единицу времени
через единицу площади поверхности, перпендикулярной
.
направлению
распространения звука, т.е. модуль среднего
значения плотности потока энергии
dW  Дж Вт 
I

2
2 

dS  dt  с  м
м 
(4)
Если интенсивность звука является объективной
величиной, характеризующей волновой процесс, то
субъективной характеристикой звука, связанной с
его интенсивностью является громкость
звука.
По физиологическому закону Вебера-Фехнера, с
ростом интенсивности звука, громкость возрастает
по логарифмическому закону, т.е. при увеличении
интенсивности в 100 раз громкость возрастает в 2
раза.
Поэтому для оценки громкости звука вводится
величина L называемая уровнем громкости
I
L  lg
I0
где
I 0  10
12
Вт
2
м
(5)
порог слышимости
Громкость звука измеряется в белах. На практике обычно
используется единица в 10 раз меньшая - децибел.
Эффект Доплера
Эффектом Доплера называется изменение частоты
колебаний, воспринимаемых приемником при
относительном движении источника и приемника
колебаний. Источник покоится, приемник движется.
v0
0 
v 2  0 v1  0

v 0  v1
v
 
 0

v0
Эффект Доплера
Источник движется, приемник покоится

1    v 2T T 
v0
2
0
v0  v2
1  
v0
v0
v
v0


 0
1   v 0  v 2 
v0  v2
v  v2
  0
v v1