Лабораторная работа Магнитное поле катушек. Закон Био
реклама

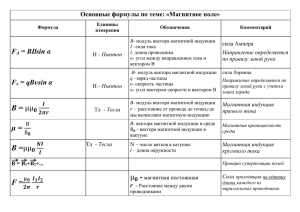
Лабораторная работа Магнитное поле катушек. Закон Био-Савара. СОДЕРЖАНИЕ: КРАТКАЯ ТЕОРИЯ ВЫПОЛНЕНИЕ РАБОТЫ ЗАДАНИЯ КОНТРОЛЬНЫЕ ВОПРОСЫ ГЛОССАРИЙ ПРИЛОЖЕНИЕ СПИСОК ЛИТЕРАТУРЫ КРАТКАЯ ТЕОРИЯ Цель работы. Исследование магнитного поля вдоль оси рамки и катушек с различными параметрами (проверка закона Био-Савара). Оборудование. Индукционные катушки, проводники электрического тока, датчик Холла, тесламетр, источник питания, универсальный держатель колец, линейка демонстрационная, мультиметр, цилиндрическая опора, штатив, прямоугольный зажим, струбцины, лабораторная подъемная платформа, переходник разъем BNC/контакт, соединительные шнуры. Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции Индукцию B проводника с током можно представить как векторную сумму элементарных индукций B , создаваемых отдельными участками проводника. На опыте невозможно осуществить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад B в магнитную индукцию B результирующего магнитного поля, создаваемый малым участком проводника с l током I 0 Il sin B 2 4r (1) Здесь r - расстояние от данного участка l до точки наблюдения, - угол между направлением на точку наблюдения и направлением тока на данном участке, - магнитная постоянная, 1,2566·10-6 Гн/м. 0 0 Таким образом, индукцию магнитного поля можно записать с помощью интеграла: 0 d l B 2 L 4 r (2) Направление вектора определяется правилом буравчика. Рис.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока: 0 1 B 2 R (3) Рис.1. Закон Био-Савара для прямолинейного проводника с током. Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля для кругового витка с током на расстоянии z от его центра. Рис.2. Схема для определения магнитного поля на оси кругового тока Рис.2. Схема для определения магнитного поля на оси кругового тока Проинтегрируем (2) по окружности. Этот расчет приводит к формуле 0 I R2 B z 2 2 3/ 2 2 R z (4) В частности, в центре кольцевого витка (z = 0) поле максимально B 0 I 2 R (5) где R – радиус кругового проводника. Для определения направления вектора B также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции. Расчеты магнитного поля токов часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае расчеты можно выполнять с помощью теоремы о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике. Поясним понятие циркуляции вектора B . Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке l этого контура можно определить касательную составляющую Bl вектора B в данном месте, то есть определить проекцию вектора B на направление касательной к данному участку контура (рис.3). Рис.3. Замкнутый контур (L) с заданным направлением обхода. Изображены токи I1, I2 и I3, создающие магнитное поле. Циркуляцией вектора B называют сумму произведений B l , взятую по всему контуру L l Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L, в то время как другие токи могут находиться в стороне от контура. Теорема о циркуляции утверждает, что циркуляция вектора B магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной 0 на сумму всех токов, пронизывающих контур: (6) B l L l ( L) 0 i В качестве примера на рис.3 изображены несколько проводников с токами, создающими магнитное поле. Токи I и I пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки - положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I 3 > 0, а I 2< 0. Ток не пронизывает контур L . 2 3 Теорема о циркуляции в данном примере выражается соотношением: Bl l 0 ( I 3 I 2 ) ( L) Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции. (7) Простейшим примером применения теоремы о циркуляции является определение магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R , лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор B направлен по касательной ( B B),а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению: l B l 2RB L l 0 ( L) откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее. (8) Этот пример показывает, что теорема о циркуляции вектора магнитной индукции B может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля. Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис.4). Рис.4. Применение теоремы о циркуляции к тороидальной катушке. Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Одна из линий индукции некоторого радиуса r1 r r2 изображена на рис.4. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис.4 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора B одинаков вдоль всей этой линии. По теореме о циркуляции можно записать: B 2r 0 IN (9) где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно: IN (10) B 0 2R Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r . Если сердечник катушки тонкий, то есть r2 r1 << r , то магнитное поле внутри катушки практически однородно. Величина n N представляет собой 2r число витков на единицу длины катушки. В этом случае B 0 In (11) В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r . Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки. На рис.5 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида. Рис.5. Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки. В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис.6. Рис.6. Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида. Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора B по контуру равна Bl , где l - длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n l , где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен Inl . Согласно теореме о циркуляции, (12) Bl Inl 0 откуда B 0 In Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки (13) ВЫПОЛНЕНИЕ РАБОТЫ Соберите установку, как показано на рисунке 7. Рис. 7. Экспериментальная установка для измерения магнитного поля Подключите модуль Тесла к модульному порту установки Кобра 3 и датчику Холла. Соедините «Датчик на 6А» с «Аналоговым входом 2/S2» установки Кобра 3. Подключите модуль для регистрации движения к установке Кобра 3 согласно рисунку 8. Подсоедините установку Кобра 3 к порту компьютера COM или USB (для подсоединения к порту USB используйте преобразователь USB - RS232 14602.10). Включите установку. Рис. 8. Схема подключения модуля для регистрации движения к установке Кобра 3 Запустите программу «Measure» для проведения измерений. Выберите в меню «Устройство» пункт «Сила/Тесла», после чего перед вами откроется окно с настройками, изображенное на рис.9. Установите параметры, как показано на рисунке 10. При установке окна 1 подтвердите показ в этом окне величины магнитной индукции; окна 2 – показ величины силы тока; окна 3 – показ положения датчика Холла. При установке окна диаграммы 1 введите параметры, как показано на рисунке 11. Рис.9. Окно определения основных параметров установки. Рис. 10. Окно определения параметров измерителя «Сила/Тесла». Рис. 11. Окно установки параметров «Параметры экрана» измерителя «Сила/Тесла». Проведите калибровку датчика перемещения. Для этого нажмите кнопку «Опции» и установите параметры в окне установки для «Угол/Расстояние» как показано на рисунке 12. Для проведения калибровки обмотайте нить, привязанную к штативу с датчиком Холла, один раз вокруг шкива датчика движения и, нажав кнопку «Старт» в окне определения параметров «Угол/Расстояние», переместите штатив с датчиком Холла точно на 30 см вдоль линейки. Нажмите кнопку «Стоп» в том же окне. Рис. 12. Окно определения параметров «Угол/Расстояние» измерителя «Сила/Тесла». Проведите калибровку датчика Холла. Для того установите параметры в окне «Калибровка», как показано на рисунке 13. Нажмите кнопку «Калибровать» в этом же окне. Проверьте, чтобы в окне «Плотность потока» были установлены mT и установите параметры в окне «Напряжение/Сила тока», как показано на рисунке 14. Рис. 13. Окно установки параметров «Калибровка» измерителя «Сила/Тесла». Рис. 14. Окно установки параметров «Напряжение/Сила тока». После внесения всех необходимых настроек, нажимаете кнопку «Далее» и можете выполнять измерения, при этом на экране компьютера откроется окно измерений, указанное на рис.15. Рис. 15. Окно измерений. При выполнении работы, чтобы сохранить полученные значения, в маленьком окошке нажимаете несколько раз с небольшим интервалом на кнопку «Сохранить значение». Обратите внимание на то, что плотность потока изменяется не сразу, поэтому кнопку «Сохранить значение» нажимайте только после того как плотность потока не будет изменяться, либо будет колебаться около определенного значения. Это необходимо для того, чтобы получить более точные данные. После того, как проделаете заданное количество измерений, нажмите также на маленьком окошке кнопку «закрыть» и на экране отобразиться результат в виде графика. Полученные результаты можно обрабатывать и на другом компьютере или с помощью более удобных программ. Чтобы получить необходимые данные, заходите в пункт «измерение» на панели инструментов, затем «экспорт данных», и в открывшемся окне указываете в каком виде хотите получить результаты: в формате выбираете «экспортировать как ч» - таблица с полученными результатами, «экспортировать как» график, «экспортировать как ме» - и таблица, и график вместе (смотрите рисунки 16, 17). Рис.16. Окно экспорта данных. Рис.17. Окно выбора формата экспорта данных. ЗАДАНИЯ Задание 1. Исследование зависимости величины магнитной индукции в центре кольцевого витка с током от радиуса кольца. Определение магнитной постоянной. Установите силу тока равную 5А, используя источник питания в качестве источника постоянного тока. Источник питания работает в режиме постоянного тока, если над регулятором тока горит красный светодиод. Установите напряжение на максимальное значение. Не меняйте значение силы тока во время эксперимента, но перед тем как разомкнуть цепь, отсоединив кольцо, обязательно уменьшите напряжение! Проведите измерение величины магнитной индукции в центре кольцевого проводника. Начните измерение, нажав кнопку «Далее». Для записи полученных экспериментальных данных следует нажать клавишу возврата или пробела, или щелкнуть на кнопке «Начать измерение». Измерения проведите для двух направлений тока и результат усредните. Аналогично проведите измерения для всех других кольцеобразных проводников. Полученные результаты занесите в таблицу 1 и представьте графически в осях и . Проведя линейную аппроксимацию, определите значение магнитной постоянной , и сравните с теоретическим значением. Таблица 1. R, см B1 , мТ B2 , мТ B , мТ 1 / R ,см-1 Задание 2. Исследование зависимости величины магнитной индукции в катушке с током от ее радиуса, длины и числа витков. Установите силу тока равную 1200 мА, используя источник питания в качестве источника постоянного тока. Источник питания работает в режиме постоянного тока, если над регулятором тока горит красный светодиод. Установите напряжение на максимальное значение. Не меняйте значение силы тока во время эксперимента, но перед тем как разомкнуть цепь, отсоединив катушки, обязательно уменьшите напряжение! Проведите измерение величины магнитной индукции вдоль оси катушки с током. Начните измерение, нажав кнопку «Далее». Запись данных начните, нажав клавишу возврата или пробела, или щелкнув на кнопке «Начать измерение». Аналогично проведите измерения для всех других катушек. Результаты представьте в виде графиков значения магнитной индукции вдоль оси катушки при: одинаковых диаметрах и количестве витков, но разной длине катушек; одинаковом количестве витков и длине, но разных диаметрах; одинаковой длине и диаметрах, но различном количестве витков. Контр. вопр. Пример полученных графиков представлен на рисунке 18. Сделайте выводы. Рис. 18. Зависимость величины магнитной индукции от длины катушки при одинаковом количестве витков (1200 мА , 2=41 мм) КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое магнитное поле? 2. Сформулируйте закон Био-Савара. 3. 4. Какие величины и параметры определяют величину магнитной индукции на оси кольцевого тока? Какие величины и параметры определяют величину магнитной индукции на оси катушки с током? 5. 6. 7. Что такое эффект Холла? Какую величину измеряют датчики Холла? Поясните графики, представленные на рисунке 18. Что является источником ошибок при измерении магнитного поля в данной лабораторной работе? ГЛОССАРИЙ Магнитное поле - одна из форм электромагнитного поля. Магнитное поле создаётся движущимися электрическими зарядами и спиновыми магнитными моментами атомных носителей магнетизма (электронов, протонов и др.) 1. 2. Вектор магнитной индукции B - основная характеристика магнитного поля, аналогичная вектору напряжённости электрического поля. Это такой вектор, что сила Лоренца (сила, действующая на заряженную частицу, движущуюся в электромагнитном поле) F , действующая на заряд q , движущийся со скоростью , равна: F q B qB sin . Теорема о циркуляции вектора магнитной индукции - циркуляция вектора B магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной 0 на сумму всех токов, пронизывающих контур: 3. B l L l ( L) 0 i Закон Био-Савара-Лапласа - физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. 4. Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, r0 - точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ): 0 I dI ; r r0 B 3 4 r r0 Эффект Холла - явление возникновения поперечной разности потенциалов (называемой также Холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Э. Холлом в 1879 году в тонких пластинках золота. 5. Принцип суперпозиции: если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности. 6. Правило Буравчика: если направление поступательного движения буравчика (винта) с правой нарезкой совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. 7. Для соленоида оно формулируется так: если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида. Теорема Гаусса - основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью. 8. Теорема Гаусса для магнитной индукции: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: B B dS 0 s Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым. приложение В данном приложении приведен пример выполнения настоящей лабораторной работы «Магнитное поле. Закон Био-Савара». ЗАДАНИЕ 1 ЗАДАНИЕ 2 ЗАДАНИЕ 1 Исследование зависимости величины магнитной индукции в центре кольцевого витка с током от радиуса кольца. Определение магнитной постоянной. Для измерений возьмем 3 кольца с разными диаметрами. R , см B1 , мТ B2 , мТ B , мТ 1/ R , см-1 12 0,008 0,001 0,0045 0,833 10 0,125 0,009 0,067 0,1 8 0,162 0,13 0,146 0,125 Построим график зависимости B от 1 / R , и проведем аппроксимацию. 0,00020 0,00018 0,00016 0,00014 Bср, мТ 0,00012 Data: Data17_B Model: Gauss Equation: y=y0 + (A/(w*sqrt(PI/2)))*exp(-2*((x-xc)/w)^2) Weighting: y No weighting 0,00010 0,00008 0,00006 Chi^2/DoF R^2 = 1 0,00004 y0 xc w A 0,00002 = -- 1.9534E-6 11.65754 2.26408 0.00054 ±1.5738E-143 ±8.116E-139 ±2.4434E-138 ±3.0846E-143 0,00000 8 9 10 11 12 13 1/R, см Таким образом, получаем экспериментальное значение магнитной постоянной 6 6 , ее теоретическое значение 1 , 26 10 1,95 10 0 0 ЗАДАНИЕ 2 Исследование зависимости величины магнитной индукции в катушке с током от ее радиуса, длины и числа витков. Рассмотрим 2 катушки с одинаковой длинной, одинаковым диаметром (d = 25мм), но разным количеством витков (катушка 1 – 150 витков, катушка 2 – 75 витков). 1. Построим график зависимости величины магнитной индукции от длины катушки. 1,4 катушка1 1,2 1,0 B,мТ 0,8 0,6 катушка2 0,4 0,2 0,0 -0,2 0 20 40 60 80 z, мм 100 120 140 Рассмотрим 3 катушки с одинаковым диаметром (d = 40 мм), с разными длинами и с разным количеством витков (катушка 3 – 300 витков, катушка 4 – 200 витков, катушка 5 – 100 витков). 2. Построим график зависимости величины магнитной индукции от длины катушки. 3,0 катушка3 2,5 катушка4 B, мТ 2,0 1,5 1,0 0,5 катушка5 0,0 0 20 40 60 80 z, мм 100 120 140 160 СПИСОК ЛИТЕРАТУРЫ 1. 2. 3. Савельев И.В. Курс общей физики. Т. 2. Гл. 6. М.: Наука, 1998 г. Ландау Л.Д. Теория поля. Т. 2. М.: Физматлит, 2001г Ресурсы интернет: http://ru.wikipedia.org