Тема: Выражения с корнями

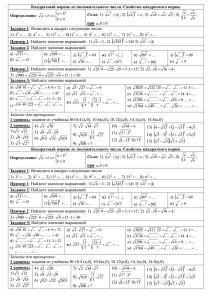
Школьный конкурс «Шаг в будующее»
Тема: Выражения с корнями
Автор: Страшков Даниил,
Ученик 8 Б класса
Руководитель: Синцова Татьяна
Витальевна, учитель математики
Г. Шарья, 2009 г.
Цели и задачи
Цель: Научиться упрощать выражения с
корнями
повышенной
сложности,
используя для упрощения различные
методы.
Задачи:
 Систематизировать
теоретический
материал для упрощения выражений с
корнями
 Использовать для упрощения выражений
различные методы
 Применить для решения нестандартные
методы
Теория
Для того чтобы преобразовывать выражения с корнями, надо знать следующие
формулы:
2=а
В этих формулах а и в – натуральные (неотрицательные) числа.
Часто для упрощений выражений с корнями нужно избавиться от
иррациональности в знаменателе. При этом часто пользуются методом
домножения на сопряжённое.
Метод домножения на сопряжённое:
(a+b)(a-b)=a2-b2
Если под корнем имеется полный квадрат, то выражение равно модулю.
ПРИМЕРЫ ВЫРАЖЕНИЙ С
КОРНЯМИ
Задание 1
Упростить выражение:
Решение:
Для упрощения этого выражения достаточно сложить три первые дроби, а
далее можно промоделировать выражение. Сложим
и
Сперва освободимся от иррациональности в знаменателе:
+
Так как знаменатель получился одинаковым, то дроби можно сложить без
домножения:
.
При
дальнейшем
сложении
Останутся лишь 2 крайних члена:
Окончательный ответ будет выглядеть так:
этих
дробей
сократятся:
Задание 2
Найти наимен ьшее значение выражения и указать пары значений
x и y, при которых оно достигается:
Так как выражения из под корня не могут быть отрицательными, то
наименьшее значение выражения – это 0. Тогда можно составить
систему уравнений:
3x-2y+10=0
x-y-3=0
3x-2y=-10
x-y=3
x=y+3
3x-2y=-10
x=y+3
3(y+3)-2y=-10
3y+9-2y=-10
Y=-10-9
Y=-19
Тогда x=-16.
Задание 3
Упростить выражение
Начнём упрощать данное выражение с конца:
=
=
Ответ: 4+√2
=
=
=4+√2
=(2
+1)2
Как видите, даже такой с виду сложный
пример легко упрощается по формуле
=
. Но что делать, если выражение под
корнем не является полным квадратом? Для
упрощения таких выражений есть другая
формула. Вот она:
=
±
Задание 4
Упростить выражение:
Упростить это выражение
по формуле полного квадрата под корнем очень сложно, поэтому
стоит воспользоваться второй формулой.
Начнём
13  48 
упрощать
13  169  48
13  169  48


2
2
по
24
 1  12  1
2
формуле
с
Вставим это в первоначальное
выражение, получим:
3  4  12
Далее упростим
4  12 
4  16  12
4  16  12

 3 1
2
2
Подставим это в первоначальное выражение, упростим:
2 3 
2 43
2 43


2
2
3
1
3 1


2
2
2
Данное выражение упрощалось довольно просто, потому что
коэффициент b отсутствовал.
Задание 5
)2=8
Проверить равенство: (
Упростим первую и вторую дроби:
)2=8
(
)2=8
(
Верно.
Выводы
 Я познакомился с различными
методами упрощения выражений с
корнями.
 Я закрепил эти методы на практике,
при этом смог научиться упрощать
выражения повышенной сложности.
Список литературы
 Алгебра: сборник заданий для подготовки к
итоговой аттестации в 9 кл./(Л.В. Кузнецова,
С.Б. Суворова и др.) – 2-е изд., - М.:
Просвещение, 2007 год.
 Методическая разработка для учащихся по
материалам заочной школы по математике,
филиал МГУ. Авторы: Иванова Е.Ю., Калинин
Д.А.
 Алгебра. 8 кл.: В двух частях. 2: Задачник
для общеобразовательных учреждений/ Аг.
Мордкович, Т.Н. Мишустина, Е.Е.
Тульчинская. – 6-е изд. – М.: Мнемозина,
2004г. – 239с.: ил.