Теория и практика педагогического тестирования. Современные
реклама

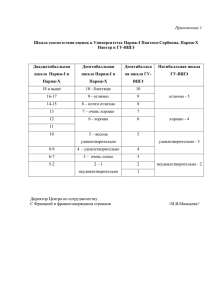
Теория и практика педагогического тестирования. Современные подходы Автор: Карданова Елена Юрьевна Часть 5 Центр повышения квалификации ГУ-ВШЭ 2010 Шкалирование результатов тестирования • С математической точки зрения процесс измерения есть отображение состояния измеряемого объекта на некоторое множество действительных чисел (или некоторое множество точек числовой оси), называемое шкалой • Шкалирование подразумевает установление правила, по которому осуществляется это отображение Уровни шкал измерения (Стивенс, 1946) • • • • номинальная порядковая интервальная шкала отношений Номинальная шкала • шкала, классифицирующая по названию • лишь способ классификации объектов или субъектов, распределения их по ячейкам классификации • числа используются просто как метки для элементов и не имеют свойств, позволяющих ввести упорядочивание элементов, равные расстояния между единицами измерения или фиксированное начало отсчета Порядковая шкала • шкала, классифицирующая по принципу «большеменьше» • единица измерения – один класс, при этом расстояние между классами может быть различным и оно нам не известно • внутри одного класса все объекты или субъекты равноправны • числа в порядковой шкале имеют свойство упорядочения, но не обладают свойством равных расстояний между единицами измерения и не имеют фиксированного начала отсчета Интервальная (метрическая) шкала • шкала, классифицирующая по принципу «больше (меньше) на определенное» • единица измерения постоянна на всех частях шкалы • позволяет количественно оценивать расстояние между объектами или субъектами • начало («ноль») этой шкалы не определено и может выбираться произвольно и не означает полного отсутствия измеряемого свойства (нет абсолютного нуля) Шкала отношений • имеет свойства упорядоченности, равных расстояний между единицами и фиксированного начала (или абсолютного нуля) • объекты или субъекты классифицируются пропорционально степени выраженности измеряемого свойства • в шкалах отношений производятся все измерения физических объектов: вес, длина, возраст в годах или днях и т.д. Четырехбалльная (2,3,4,5) шкала оценивания знаний • является порядковой (не обладает метрическими свойствами) • годится только для упорядочивания учащихся, арифметические операции над ее индексами не имеют смысла • обладает очень низкой чувствительностью Шкала первичных баллов • является порядковой (не обладает метрическими свойствами) • позволяет только ранжировать объекты измерений, то есть упорядочить их в порядке возрастания (или убывания) их оценок • не позволяет объективно определить, насколько один испытуемый лучше другого Шкала тестовых баллов (IRT) • является интервальной • дает возможность перейти от ранжирования участников тестирования к измерению их уровня подготовленности • есть единица измерения (один логит) • легко переводится в любую другую, удобную для восприятия шкалу (например, стобалльную) Интерпретация результатов тестирования • В тестах с нормативно-ориентированной интерпретацией главная задача – определение сравнительного места каждого из тестируемых в общей группе испытуемых. Именно поэтому необходимо по возможности использовать нормы, отражающие результаты выполнения теста большой репрезентативной выборкой испытуемых. • В тестах с критериально-ориентированной интерпретацией задача - сопоставление учебных достижений каждого ученика с планируемым к усвоению объемом знаний, умений и навыков. Основной проблемой является установление проходного балла, отделяющего тех, кто освоил проверяемый материал, от тех, кто не освоил. Установление норм выполнения теста • Нормы – это множество показателей, которые устанавливаются эмпирически по результатам выполнения теста определенной выборкой испытуемых • Разработка и процедуры получения этих показателей составляют процесс нормирования (или стандартизации) теста • Наиболее распространенными нормами являются среднее значение и стандартное отклонение по множеству индивидуальных баллов Требования к нормам • дифференцированность: нормы должны отражать специфику программы подготовки учеников • соответствие реальным требованиям: нормы должны отражать реальный контингент испытуемых, реальную ситуацию • Репрезентативность: нормы должны устанавливаться на репрезентативной выборке, отражающей генеральную совокупность и обеспечивающей несмещенные оценки Методы формирования выборки • • • • доступная выборка простая случайная выборка систематическая выборка стратифицированная случайная выборка Преобразование первичных баллов (шкалирование) Цели: • уточнить место, занимаемое испытуемым в нормативной выборке • сравнить результаты испытуемых, полученные по различным тестам • улучшить восприятие тестовых баллов и их сопоставимость Важно: никакое преобразование первичных результатов не повышает уровень измерений (т.е. не приводит к интервальной шкале) Наиболее известные преобразования первичных баллов • процентильный ранг • линейная Z-оценка • оценки, которые являются линейным преобразованием z-оценки (Т-шкала, оценки стандартного IQ и т.д.) • шкалы станайнов и стенов Шкала процентильных рангов • Процентильный ранг, соответствующий данному первичному баллу, показывает процент испытуемых в нормативной выборке, результаты которых не выше данного первичного балла Пример построения шкалы процентилей Первичный балл Частоты Кумулированные частоты Процентильные ранги 3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 2 2 3 4 3 3 2 1 1 1 1 1 2 4 6 9 13 16 19 21 22 23 24 25 1 6 12 20 30 44 58 70 80 86 90 94 98 Недостатки шкалы процентильных рангов Шкала процентильных рангов нелинейна, т.е. в различных областях шкалы первичных баллов увеличение на 1 балл может соответствовать различным увеличениям на шкале процентилей Область распределения Первичный балл Процентильный ранг Доверительный интервал первичного балла (x±σ) Процентильный интервал Высокая Средняя Низкая 41 28 21 94 38 14 38-44 25-31 17-23 84-99 27-50 8-22 Z-шкала • Цель: выявление места результата i-го ученика в сравнении с результатами других • среднее значение Z-показателей равно 0, а стандартное отклонение равно 1 • отрицательные значения Z указывают на результаты ниже среднего, а положительные — на результаты, выше среднего значения по группе Интерпретация результатов тестирования Субтест Первичный балл Z-оценка Математика Языки Физика Общественные науки 102 80 115 95 -0,31 1,25 0,10 0,83 Нормальное распределение Z-оценок Некоторые свойства нормального распределения • 68 % площади под кривой лежит в пределах одного стандартного отклонения, откладываемого влево и вправо от среднего значения • 95 % площади под кривой лежит в пределах двух стандартных отклонений, откладываемых влево и вправо от среднего значения • 99,7 % площади под кривой лежит в пределах трех стандартных отклонений, откладываемых влево и вправо от среднего значения Недостатки Z-оценок • могут принимать дробные и отрицательные значения, с которыми сложно работать при подсчетах и которые трудно интерпретировать для пользователей тестов • округление Z-оценок до целых значений не всегда допустимо, т.к. основную цель создания тестов составляет выявление различий в подготовке испытуемых Преобразования Z-оценок • используемое преобразование должно быть линейным, чтобы сохранить форму распределения Z-оценок • общая формула преобразования имеет вид: Z1=M + σ·Z, где Z1 – преобразованная оценка, М – новое среднее, σ- новое стандартное отклонение Виды шкал • T-шкала (McCall, 1939): выбирается среднее значение М = 50 и стандартное отклонение σ = 10: Z1=50 + 10·Z • Шкала СЕЕВ (ETS): выбирается среднее значение М = 500 и стандартное отклонение σ = 100: Z1=500 + 100·Z • Шкала IQ (Weshler, 1939). Выбирается среднее значение М = 100 и стандартное отклонение σ = 15: Z1=100 + 15·Z Шкалы станайнов и стенов • удобны для сообщения тестовых результатов, обладают очевидной простотой • состоят из отдельных целых чисел - от 1 до 9 или от 1 до 10 • весь массив результатов делится на 9 или 10 частей Шкала станайнов • станайн 1 присваивается 4% самых худших результатов, станайн 9 - 4% самых лучших • станайны 2 и 8 присваивают следующим за худшими и лучшими 7% результатов соответственно • станайны 3 и 7 - следующим за ними 12% результатов • станайны 4 и 6 - следующим 17% результатов • станайн 5 присваивается 20% средним результатам группы Шкала стенов (шкала Кеттела) • весь массив результатов делится на 10 частей с интервалом 0,5 стандартного отклонения • В шкале стенов среднее арифметическое принимается равным 5,5, а расстояние между двумя соседними стандартными единицами равно 0,5 Одиннадцатибалльная шкала • получают из шкалы станайнов путем выявления по одному проценту самых сильных и самых слабых испытуемых и присвоения им соответственно максимального и минимального балла Соотношения между оценками некоторых шкал 5-б. шкала 2 3 4 5 11-б. шкала Оценочный эквивалент 1 Низшая оценка 2 Z-оценка Процент Станайн испытуемых Z< -2,25 1 Неудовлетворительно -2,25 <Z< -1,75 3 1 3 Малоудовлетворительно -1,75 <Z< -1,25 7 2 4 Удовлетворительно -1,25<Z<-0,75 12 3 5 Ниже среднего -0,75 <Z< -0,25 17 4 6 Среднее -0,25 <Z< 0,25 20 5 7 Выше среднего 0,25 <Z< 0,75 17 6 8 Хорошо 0,75 <Z< 1,25 12 7 9 Очень хорошо 1,25 <Z< 1,75 7 8 10 Отлично 1,75<Z<2,25 3 9 11 Высшая оценка 2,25 < Z 1 Установление проходного балла • Используются при критериальноориентированном тестировании • Все методы делятся на абсолютные и относительные • Все методы вовлекают в процедуру определения проходного балла экспертов Методы, центрированные на заданиях • Метод Nedelsky (1954) • Метод Angoff (1971) • Метод Ebel (1972) Методы, центрированные на испытуемых (Nedelsky, 1954; Zieky, Livingston, 1977) • Метод контрастных групп • Метод граничных групп