Теория Автоматов1_11
реклама

Теория Автоматов
Конечные функциональные
преобразователи
Функциональная полнота
образована соответствии с определением 1.2,
функционально полным набором (или базисом)
называется такое множество булевых функций,
суперпозицией которых могут быть выражены любые
булевы функции. Один из таких базисов — базис
Буля — нами определен: это три функции И, ИЛИ,
НЕ. Исследование проблем, связанных с базисами,
чрезвычайно важно для практики: функции базиса —
это тот полный набор строительных блоков, из
которых можно строить все другие двоичные функции от любого числа переменных, а следовательно,
реализовывать любые конечные функциональные
прели.
Функциональная полнота
Важными для практики и интересными с теоретической точки
зрения являются
вопросы:
Q почему функции И, ИЛИ, НЕ такие особенные, что с их
помощью можно построить любую другую булеву функцию?
Q существуют ли еще какие-нибудь базисы, кроме базиса
Буля? Q является ли некоторый заданный базис минимальным
(то есть не содержит ли
он излишних функций, выражающихся суперпозицией других)?
Q как проверить, является ли заданный набор функций базисом,
и если не является, как дополнить его другими функциями,
чтобы получившееся множество составило базис?
Введем некоторые определения и обозначения
Функциональная полнота
Определение 1.5. Замыканием множества М булевых функций
назовем такое множество булевых функций, которые можно
получить суперпозицией функций из М. Замыкание множества
М обозначим [М].
Пусть В — множество всех двоичных функций. Очевидно, что
множество М двоичных функций будет базисом, только если [М]
= В. Рассмотрим свойства замыканий двоичных функций.
Теорема 1.4. Пусть М, N с В. Тогда:
а) Мс[М];
б) [[М]] = [М]; [В]=В;
в) McN=>[M]c[Nj
г) [М]СВ;
д) если М — базис и М с [N], то N — тоже базис
Функциональная полнота
Доказательство теоремы просто. Утверждения а),
б), в) и г) следуют непосредственно из определений.
Докажем д). М с [N] => [М] с [[N]~] на основании в),
следовательно, [М] с [N] на основании б). Но
поскольку М — базис, [М] = В. Отсюда В с [N] , но
поскольку г) [N] с В, то [N] = В.
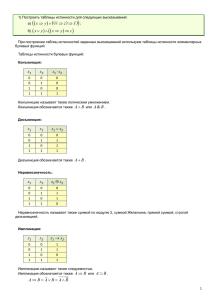
Попробуем найти другие базисы, отличные от базиса
Буля. Согласно законам де Моргана, -i(p v q) = -ф-iq.
Следовательно, р v q = -i(-ip-iq). Таким образом, дизъюнкция выражается через конъюнкцию и отрицание,
следовательно, суперпозицией функций {И, НЕ}
можно построить все функции базиса Буля — то есть
ИЛИ можно выбросить из этого базиса. Некоторые
другие базисы представлены в табл. 1.7. Их
обоснование очевидно.
Функциональная полнота
Рассмотрим конъюнктивный базис. Он является
минимальным, поскольку выбрасывание из
множества {И, НЕ} любой функции превращает
оставшееся одноэлементное множество в не-базис.
Действительно, например, с помощью суперпозиции
произвольного числа функций НЕ можно построить
только функцию НЕ и тождественную функцию
ИДЕНТ, то есть f (х) = х. Заметим, что суперпозицией
унарных функций множества М в {ИДЕНТ, НЕ} можно
построить только функции этого множества.
Множество булевых функций, обладающее этим
свойством, называется замкнутым классом двоичных
функций.
Функциональная полнота
Функциональная полнота
Пример 1.8
Конъюнкции, то есть все функции вида х, л х2 л . . . л
хт, тоже составляют замкнутый класс. Очевидно,
однако, что, например, функцию, которая на наборе
(0, 0, . . . , 0) имеет значение 1, нельзя представить
суперпозицией таких функций. Таким образом, {И} не
является базисом, следовательно, конъюнктивный
базис {И, НЕ} является минимальным.
Рассмотрим более подробно базис Жегалкина.
Алгебра Жегалкина и линейные
функции
Алгебра Жегалкина — это алгебра над множеством
двух бинарных булевых функций (И, ©) и нульарной
функции 1. Легко проверить следующие соотношения
в этой алгебре:
Справедливы в этой алгебре, конечно, и все
соотношения табл. 1.4, включающие эти функции.
Если в произвольной формуле, включающей только
функции базиса Жегалкина, раскрыть скобки, то
получим бесскобочную формулу, имеющую вид
суммы (по модулю два) произведений, то есть
некоторый полином. Он называется полиномом
Жегалкина
Алгебра Жегалкина и линейные
функции
Пример 1.9
Алгебра Жегалкина и линейные
функции
Теорема 1.5. Любая булева функция может быть
представлена в виде полинома Жегалкина, причем
единственным образом.
Доказательство. Существование полинома для любой функции
гарантируется тем, что функции {И, 0,1} образуют базис. Далее,
легко видеть, что число возможных членов в полиноме с m
переменными равно 2т. Поэтому число различных полиномов
Жегалкина от m переменных равно 2 в степени 2т, то есть числу
возможных двоичных функций от m переменных. Поскольку
одна и та же формула не может представлять различные
функции, то тем самым между множествами двоичных функций
и полиномов Жегалкина от m переменных установлено
взаимнооднозначное соотношение.
Пример 1.10
Построим для функции f (p, q, r) = -ip vq0rq(pvr) примера 1.2
полиномом Жегалкина непосредственно из таблицы истинности
(см. табл. 1.3). Эту таблицу повторим здесь.
Алгебра Жегалкина и линейные
функции
Таблица 1.8
р
0
0
0
0
1
1
1
1
q
0
0
1
1
0
0
1
1
г
0
1
0
1
0
1
0
1
f
1
1
1
0
0
0
1
0
Алгебра Жегалкина и линейные
функции
Будем искать коэффициенты полинома
,:.
f (p, q, r) = a0 0appeaqq0arreapqpqe aprpr0 aqrqr0 a^pqr
. , ,.f
Всего коэффициентов 8, каждый коэффициент может быть 0
или 1, число возможных вариантов равно 28 =* 256 — как раз
столько, сколько всех возможных булевых функций от трех
переменных. Для нахождения коэффициентов заданной функции используем таблицу ее значений.
Искомые коэффициенты последовательно найдем из
следующей системы уравнений:
f (0,0,0) = 1 = a0; отсюда а0 = 1;
f (1,0,0) = 0 = а0Фар = 10ap; отсюда ар =1;
Г(0,1,0) = 1 = а00ач=10ач;отсюдаач==0;
f (0,0,1) = 1 = a0 ©ar = 10ar; отсюда ar = 0;
Алгебра Жегалкина и линейные
функции
Г(1,1,0) = 1 =
а0Фар0ачеар(1=1е1еоеа1Х1;отсюдаарч=1;
f(l,0,l) = 0 = a0®ap0ar0apr =101000apr; отсюда
apr =0;
Г(0,1,1) = 0 = а00ач0аг0ачг =
100000ачг;отсюда aqr =1Найденное
представление совпадает с представлением,
полученным для этой функции ранее
аналитически: f (p, q, г) = 1 Ф р Ф pq 0 qr .
Булева функция, полином Жегалкина которой
имеет вид а0 ©Хах1х{, называется линейной.