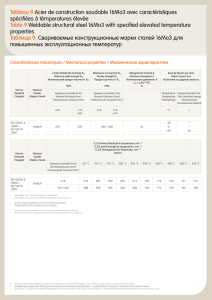
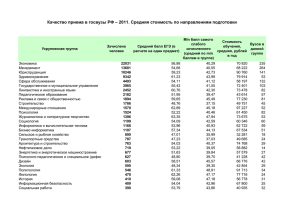
Методы оптимизации
реклама

Теория оптимального управления экономическими системами - II Проф. В.П. Кривошеев Динамическое программирование в непрерывной форме. Уравнение Беллмана Решается задача оптимального управления t J F ( y (t ), u(t ), t )dt min (max), 0 ut y(0) = y0, dyi(t)/dt = fi(y(t),u(t),t), i = 1,…,n, y(tk) = yk. В основе динамического программирования лежит принцип оптимальности в соответствии с которым нужно оптимальным образом перевести систему из состояния y()в конечное состояние y(tk) не зависимо от того, каким образом система пришла из исходного состояния y(0) в состояние y(). Динамическое программирование в непрерывной форме. Уравнение Беллмана y (t ) y* (t ) y* (t ) y (0) y (t ) 0 t tk Вариация функции Динамическое программирование в непрерывной форме. Уравнение Беллмана Математически принцип оптимальности реализуется через выражение: t min J min [ F ( y (t ), u(t ), t )dt min F ( y (t ), u(t ), t )dt ]. u(t ) u(t ) 0 u(t ) Пусть - малая величина. Обозначим t (, y* ()) min F ( y (t ), u(t ), t )dt , u(t ) t (0, y* (0)) min F ( y (t ), u(t ), t )dt. u(t ) 0 Тогда t (0, y* (0)) min [ F ( y (t ), u(t ), t )dt (, y ())]. u(t ) 0 Динамическое программирование в непрерывной форме. Уравнение Беллмана Разложим функцию (, y()) в ряд Тейлора относительно состояния t = 0, y(0) = y0 по степеням y(t) и t. n (, y ()) (0, y (0)) yi i 1 (t , y (t )) (t , y (t )) t . t 0 t 0 yi t y y (0) y y (0) Примем, что t = . Заметим, что yi (t ) dyi (t )dt t , или yi (t ) fi ( y(t ), u(t ), t ) t. С учетом малости можно записать F ( y (t ), u(t ), t )dt F ( y (0), u(t ), t ) t F ( y (0), u(t ), t ) . 0 Динамическое программирование в непрерывной форме. Уравнение Беллмана Теперь min(J(y(0),u(t))), с учетом выше приведенных выражений, можно записать в виде (0, y* (0)) min [ F ( y (0), u(t ), t ) (0, y* (0)) u (t ) n (((t , y (t )) / yi ) fi ( y (t ), u(t ), t )) t 0 i 1 y y (0) ((t , y (t )) / t t 0 ]. y y (0) Динамическое программирование в непрерывной форме. Уравнение Беллмана Так как (0, y(0)) не зависит от u(t), а содержится во всех составляющих правой части записанного выше уравнения, то это уравнение приводится к виду ((t , y (t )) / t t 0 min [ F ( y (0), u(t ), t ) t 0 u (t ) y y ( 0) y y ( 0) n (( (t , y (t )) / yi ) f i ( y (t ), u(t ), t )) t 0 ]. i 1 y y (0) Учтем тот факт, что разложение условно оптимальной величины функционала, записанной для условного состояния в какой-то момент времени t (в приведенном случае y()), Динамическое программирование в непрерывной форме. Уравнение Беллмана можно разложить в ряд Тейлора относительно оптимального состояния системы в момент времени t- при y*(t), т.е. ( (t , y (t )) / t min [ F ( y (t ), u(t ), t ) u (t ) n (( (t , y (t )) / yi ) f i ( y (t ), u(t ), t ))]. i 1 Полученное уравнение называется уравнением Беллмана. Оно является уравнением в частных производных. Решением этого уравнения есть функции u*(t), доставляющие экстремум функции и функции состояния системы y*(t), описывающие оптимальную траекторию движения системы из исходного y0 в конечное состояние yk. Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме Для решения уравнения Беллмана, кроме условий y(0) = y0 и y*(tk) = yk, нужно иметь значение функции (t, y(t)) и значения ее производных (t, y(t))/yi, i = 1,…,n, и (t,y(t))/t в один из граничных моментов времени tн = 0 или tk. Заметим, что (tk, y(tk)) = 0 по определению. В силу этого имеет место тождество (t , y (t )) / yi t t k y y (tk ) 0, i 1,..., n. Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме Теперь из самого уравнения Беллмана следует (t , y (t )) / t t t max ( F ( y (t ), u(t ), t ) t t . k k u y y (t k ) y y (t k ) Получены все условия для решения уравнения Беллмана. Решение уравнение Беллмана выполняется известными методами решения систем дифференциальных уравнений в частных производных. Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме Покажем что уравнение Беллмана при некоторых допущениях может быть приведено к уравнениям Эйлера. Запишем уравнение Беллмана в виде двух видов уравнений: Первый вид: (t , y (t )) / t F ( y (t ), u* (t ), t ) n Второй вид: ((t , y (t )) / yi ) f i ( y (t ), u* (t ), t ). i 1 F ( y (t ), u(t ), t ) / u j n (t , y (t )) / yi f i ( y (t ), u(t ), t ) / u j 0, j 1,..., r. i 1 Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме Управления, удовлетворяющие уравнениям второго вида, обозначим u*(t). В первом уравнении управления u*(t) удовлетворяют условиям правой части уравнения Беллмана, выраженным уравнениями второго вида. Теперь продифференцируем уравнение первого вида по переменным состояния и введем обозначения: k(t) = -(t, y(t))/yk, k = 1,…,n, 0 = -1. Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме (t , y (t )) ( ) / yk F ( y (t ), u* (t ), t ) / yk t n ((t , y (t )) / yi ) / yk f i ( y (t ), u* (t ), t ) i 1 n ((t , y (t )) / yi ) (fi ( y (t ), u* (t ), t ) / yk ), k 1,..., n. i 1 Принимая допущения, что ( (t , y(t )) / yi ) / yk 0, с учетом принятых выше обозначений, получим d k (t ) / d t 0 (F ( y (t ), u* (t ), t ) / yk n i (t )( fi ( y (t ), u* (t ), t ) / yk , k 1,..., n, i 1 n 0 (F ( y (t ), u(t ), t ) / u j i ( fi ( y (t ), u* (t ), t ) / u j ) 0, i 1 j 1,..., r. Алгоритм решения задачи оптимального управления методом динамического программирования в непрерывной форме Полученные уравнения являются уравнениями Эйлера в задаче оптимального управления. Таким образом, показано, что классическое вариационное исчисление, принцип максимума и уравнение Беллмана при некоторых допущениях позволяют выразить условия экстремума функционала в задаче оптимального управления идентичными уравнениями. Статическая оптимизация Виды функций по количеству экстремумов - унимодальные, имеющие один экстремум - полимодальные, более одного экстремума Виды экстремумов и наилучших значений функции - локальный минимум полимодальной функции в точке ui*, если Q(ui* u ) Q(ui* ) Q(ui* u ), или dQ( u) / du u* u 0 и dQ(ui ) / du u* u 0; i i - локальный максимум полимодальной функции в точке ui*, если Q(ui* u ) Q(ui* ) Q(ui* u ) , или dQ( u) / du u* u 0 и dQ(ui ) / du ui* u 0 , i где i=1,2,…,k – число локальных экстремумов. Виды экстремумов и наилучших значений функции - супремум (sup Q (u)) при umin, если Q(umin ) max (Q(ui ), Q(umin ), Q(umax )) ; i, min, max - супремум (sup Q (u)) при umax, если Q(umax ) max (Q(ui ), Q(umin ), Q(umax )) ; i, min, max - инфимум (inf Q (u)) при umin, если Q(umin ) min (Q(ui ), Q(umin ), Q(umax )) ; i, min, max - инфимум (inf Q (u)) при umax, если Q(umax ) min (Q(ui ), Q(umin ), Q(umax )) ; i, min, max - глобальный минимум в точке ug, если Q(ug ) min (Q(u*i ), Q(umin ), Q(umax )) ; i , i 1, 2,..., k , min, max - глобальный максимум в точке ug, если Q(ug ) max i , i 1, 2,..., k , min, max (Q(u*i ), Q(umin ), Q(umax )) . Постановка задачи статической оптимизации Q(X, U) min(max) U yi=φi(X, U) , i=1,…,n, yi yiзад, i=1,…,k, yi yiзад, i=k+1,…,p, Ujmin Uj Ujmax, j=1,…,r, где X=(x1,…,xn) – вектор внешних возмущающих воздействий, U=(u1,…,ur) – вектор управляющих воздействий, Y=(y1,…,yp) – вектор выходных переменных, yiзад - заданные значения выходных переменных, Ω - область допустимых управлений. Требуется найти такие значения управляющих воздействий U=(u1,…,ur), при которых выполняются приведенные выше условия, а критерий оптимальности Q принимает минимальное (максимальное) значение. Методы статической оптимизации 1. Классический метод исследования функции на экстремум 2. Методы нелинейного программирования: - численные методы решения одномерной задачи статической оптимизации; - численные методы решения многомерной задачи статической оптимизации 3. Линейное программирование 4. Динамическое программирование в дискретной форме Классический метод исследования функций на экстремум Необходимые и достаточные условия экстремума функции одной переменной Q=Q(u) Необходимое условие: dQ(u) / du u* 0. Достаточное условие: Если при u=u* впервые в порядке возрастания k d k Q(u ) / du k u* 0, где k – четное, то Q=Q(u) имеет экстремум. Причем, если dQ(u) / du u* 0, то Q(u)min, а если dQ(u) / du u* 0 , то Q(u)max. Если при u=u* впервые в порядке возрастания k d k Q(u) / du k u* 0, где k – нечетное, то Q=Q(u) не имеет экстремума. Примеры исследования функции одной переменной на экстремум Пример 1. Q = (1-u)3. Необходимое условие экстремума dQ(u) / du u* 0: 3(1-u*)2(-1) = 0, u* =1. Достаточное условие экстремума d 2Q(u ) / du 2 u* = 6(1-u*) = 6(1-1) = 0, d 3Q(u ) / du 3 u* 6 0. k = 3 – нечетное. Ответ: при u* =1 исследуемая функция не имеет экстремума. Примеры исследования функции одной переменной на экстремум Пример 2. Q = (1-u)4. Необходимое условие экстремума dQ(u) / du u* 0: 4(1-u*)3(-1) = 0, u* =1. 2 2 Достаточное условие экстремума d Q(u ) / du u* = 12(1-u*)2 = 12(1-1)2 = 0, d 3Q(u) / du 3 u* = 24(1-u*) = 24(1-1) = 0, d 4Q(u ) / du 4 u* = 24 = 0. k = 3 – нечетное. Ответ: при u* =1 исследуемая функция имеет минимум. Классический метод исследования функций на экстремум Необходимые и достаточные условия экстремума функции нескольких переменных Q=Q(U) = Q(u1,…,ur). Необходимое условие: Q(U ) / u j U * 0, j 1,..., r , U * (u1* ,..., ur* ) . Достаточное условие: Если при U=U* все диагональные миноры матрицы Гессе (Г): 2 2Q (U ) Q (U ) u1u1 u1u r 2 2 Q ( U ) Q ( U ) u u u u r 1 r r (Г) строго положительны, то функция Q=Q(U) имеет минимум. Если при U=U* нечетные диагональные миноры матрицы (Г) строго отрицательные, а четные строго положительные, то функция Q=Q(U) имеет максимум. Примеры исследования функции нескольких переменных на экстремум классическим методом Пример 1. Q = u1+2u12+u2+4u22+3u1u2 Необходимое условие экстремума: * * Q(U ) / u1 u1*,u 2 * 0 , 1+4u1 +3u2 = 0; , 1+8u2*+3u1* = 0; Q(U ) / u2 u1*,u 2 * 0 4 3 32 9 23 3 8 2 4 3 1 4 3 1 1 1 , , 1 3 8 3 5 1 8 u1* = 1 / = -5/23, u2* = 2 / = -1/23. , Примеры исследования функции нескольких переменных на экстремум классическим методом Пример 1. Q = u1+2u12+u2+4u22+3u1u2. Достаточное условие экстремума: 2Q (U ) / u1u1 u1*,u 2 * 4; 2Q(U ) / u1u2 u1*,u 2 * 3; 2Q(U ) / u2u1 u1*,u 2 * 3; 2Q (U ) / u2u2 u1*,u 2 * 8; Матрица (Г): 2Q (U ) 2Q (U ) u1u1 u1u 2 4 3 2 2 Q (U ) Q (U ) u 2 u1 u 2 u 2 3 , 8 1-ый диагональный минор равен 4>0, 2-ой диагональный минор равен 48-33=32-9=23>0. Ответ: при u1* = -5/23, u2* = -1/23 исследуемая функция имеет минимум. Примеры исследования функции нескольких переменных на экстремум классическим методом Пример 2. Q = u1-2u12+u2+4u22+3u1u2 Необходимое условие экстремума: Q(U ) / u1 u1*,u 2 * 0 , 1-4u1*+3u2* = 0; Q(U ) / u2 u *,u * 0 , 1+8u2*+3u1* = 0; 1 4 3 2 2 3 32 9 41, 8 4 3 1 43 7, 1 1 1 3 8 3 5 1 8 u1* = 1 / = 5/41, u2* = 2 / = -7/41. , Примеры исследования функции нескольких переменных на экстремум классическим методом Пример 2. Q = u1-2u12+u2+4u22+3u1u2. Достаточное условие экстремума: 2Q(U ) / u1u1 u1*,u 2 * 4; 2Q(U ) / u1u2 u1*,u 2 * 3; 2Q(U ) / u2u1 u1*,u 2 * 3; 2Q (U ) / u2u2 u1*,u 2 * 8; Матрица (Г): 2Q (U ) 2Q (U ) u1u1 u1u 2 4 2 2 3 Q (U ) Q (U ) u 2 u1 u 2 u 2 3 , 8 1-ый диагональный минор равен –4<0, 2-ой диагональный минор равен -48-33=-32-9=-41<0. Ответ: при u1* = 5/41, u2* = -7/41 исследуемая функция не имеет экстремума. Аналитическое решение задачи на условный экстремум - Метод множителей Лагранжа. - Условие Куна-Таккера Аналитическое решение задачи на условный экстремум при условиях типа равенства: Q=Q(U) min, U j(U) = 0, j = 1,…,m, U = (u1,…,ur), m < r. Задача решается методом множителей Лагранжа. Метод множителей Лагранжа 1. Составляется функция Лагранжа m L(U , λ) Q(U ) j j (U ) j 1 где j, j=1,…,m,- множители Лагранжа. 2. Совместно решается система уравнений: L(U,) / ui=0, i=1,…,r, j(U) = 0, j = 1,…,m. Пример решения задачи методом множителей Лагранжа Q = u12+u22 , u1+u2 – 1 = 0. Функция Лагранжа L=Q(u1,u2)+ (u1,u2)= u12+u22 + (u1+u2 – 1), L/u1= 2u1*+ = 0, L/u2= 2u2*+ = 0, Пусть 0, тогда u1 = /2, u2 = /2, u1 = u2, - u1 - u2 + 1= 0, u1* = u2* = 0,5. Аналитическое решение задачи на условный экстремум - Метод множителей Лагранжа. - Условие Куна-Таккера Аналитическое решение задачи на условный экстремум при условиях типа неравенств: Q=Q(U) min, U j(U) 0, j = 1,…,m, U = (u1,…,ur). Задача решается с использованием условий Куна-Таккера. Условия Куна-Таккера Рассматривается задача выпуклого программирования Q=Q(U) min, U j(U) 0, j = 1,…,m, U = (u1,…,ur), где Q(U) и j(U) - выпуклые дифференцируемые функции. Алгоритм решения задачи. 1. Составляется функция Лагранжа: m L(U , λ) Q(U ) j j (U ) j 1 где j, j=1,…,m,- множители Лагранжа. Условия Куна-Таккера 2. Совместно решается система уравнений и неравенств: L(U,) / ui=0, i=1,…,r, jj(U) = 0, j = 1,…,m, j 0, j = 1,…,m, j(U) 0, j = 1,…,m. К определению выпуклости функции Пусть 0 1. Произвольную точку на линии ab можно описать как a+(b-a)(1-)= a+(1-)b, т.е. при = 0 это точка b, а при = 1 это точка а. В случае нелинейной функции ее значение в точке с = a+ (1-)b есть Q[ a+(1)b]. К определению выпуклости функции Значение линейной функции, проходящей через точки a и b, в точке с равно Q(a)+(Q(b) - Q(a))(c-a)/(b-a) = Q(a)+(Q(b) - Q(a))[a+(1-)b-a]/(b-a) = Q(a)+(Q(b) - Q(a))(1-) = Q(a)+ (1-)Q(b). Сравнивая значения исходной функции с линейной функцией в точке с можно записать условие выпуклости функции: если имеет место Q( a+(1-)b)< Q(a)+ (1-)Q(b), то исходная функция выпукла (лежит ниже линейной функции на отрезке [a,b]). Примеры решения задачи с использованием условия Куна-Таккера Пример 1. Q = u12+u22 min, u1, u2 u1+u2 1, или (u1,u2)= u1+u2 – 1 0, L=Q(u1,u2)+ (u1,u2)= u12+u22 + (u1+u2 – 1). Условия Куна-Таккера: * 0, L(U,) / uj = 0, *(u1*,u2*) = 0, j=1,2. Решение: L/u1= 2u1*+ = 0, L/u2= 2u2*+ = 0, (u1+ u2-1) = 0, u1+u2 – 1 0. Пусть = 0, тогда u1*= 0, u2*= 0. Ограничение u1+u2 – 1 0 в точке u1= 0, u2= 0 пассивно. Примеры решения задачи с использованием условия Куна-Таккера Пример 1 (продолжение): Пусть 0, тогда u1+u2 – 1 = 0, 2u1= - , т.к. > 0, то u1< 0; 2u2= - , т.к. > 0, то u2< 0. В этом случае не выполняется условие u1+u2 – 1 = 0. Пример 2. Q = u12+u22 min, u1, u2 u1+u2 1, или (u1,u2)= -u1-u2 + 1 0, L=Q(u1,u2)+ (u1,u2)= u12+u22 + (-u1-u2 + 1). Условия Куна-Таккера: * 0, L(U,) / uj = 0, *(u1*,u2*) = 0, j=1,2. Примеры решения задачи с использованием условия Куна-Таккера Пример 2 (продолжение): Решение: L/u1= 2u1 - = 0, L/u2= 2u2 - = 0, (-u1 - u2 + 1) = 0, -u1-u2 +1 0. Пусть = 0, тогда u1+ u2 -1 =0. Ограничение -u1-u2 +1 0 в точке u1= 0, u2= 0 не выполняется. Пусть 0, тогда u1 = /2,u2 = /2, u1= u2; -u1-u2 +1 = 0, u1*, u2*=1/2. Ограничение -u1-u2 +1 0 в точке u1= 1/2, u2= 1/2 активно. Численные методы решения одномерных задач статической оптимизации Сканирования (с постоянным и переменным шагом). Половинного деления исходного интервала, содержащего экстремум. «Золотого» сечения. С использованием чисел Фибоначчи. Метод сканирования с постоянным шагом Функция Q(u), a u b. Алгоритм поиска: 1. Задается точность вычисления оптимального значения uu*. 2. Интервал (b-a) делится на N отрезков, N (b-a)/ . 3. В каждой точке ui =a+i (b-a) / N , i =0,1,…, N, вычисляется функция Q(ui) и выбирается Q(u*) из условия Q(u* ) = max Q(ui) или ui Q(u* ) = min Q(ui). ui Метод сканирования с переменным шагом Функция Q(u), a u b. Алгоритм поиска: 1. Задается точность вычисления оптимального значения uu*. 2. Интервал (b-a) делится на S отрезков, S << (b-a)/ . 3. В каждой точке u1i =a+i(b-a) / S, i =0,1,…,S, вычисляется функция Q(u1i) и выбирается Q(u1*) из условия Q(u1*) = max Q(u1i) или ui Q(u1*) = min Q(u1i). ui 4. Назначают границы нового интервала поиска a1 и b1 из условия: a1 = u1k-1, b1 = u1k+1, где u1k-1 и u1k+1 есть значения, соседние с u1* = u1k. Метод сканирования с переменным шагом При максимизации функции Q=Q(u) max, u Q(u1k-1) < Q(u1k) = Q(u1*) > Q(u1k+1). При минимизации функции Q=Q(u) min, u Q(u1k-1) > Q(u1k) = Q(u1*) < Q(u1k+1). 5. Пункты 2-4 повторяются для интервалов (b1 - a1), (b2 – a2),…, (bj - aj). 6. Расчет заканчивается при условии bj - aj . Метод половинного деления Q=Q(u) max(min), a u b Q(u) u11 a u12 b u Поиск методом половинного деления Метод половинного деления Q=Q(u) max(min), a u b Алгоритм поиска: 1. Делится интервал (b-a) пополам u1 = a+(b-a)/2. 2. Внутри интервала выбираются две точки u11 = u1 - и u12 = u1 +, где = (0.01-0.25). 3. Рассчитываются Q(u11) и Q(u12). 4. Определяются границы нового интервала a1 и b1. Если Q=Q(u) max, то при Q(u11) > Q(u12) выбираем a1 = a, b1 = u12; при Q(u11) Q(u12) выбираем a1 = u11, b1 = b; Если Q=Q(u) min, то при Q(u11) > Q(u12) выбираем a1 = u11, b1 = b; при Q(u11) Q(u12) выбираем a1 = u11, b1 = u12; 5. Проверяется условие окончания поиска b1 - a1 . 6. Для каждого нового интервала (bi - ai) повторяются пункты 1-4 до выполнения условия bi - ai . Метод «золотого» сечения Q=Q(u) max(min), a u b Q(u) 0.62(b-a) 0.38(b-a) 0.38(b-a) u a u11 u 12 b Поиск методом «золотого» сечения Метод «золотого» сечения Q=Q(u) max(min), a u b Алгоритм поиска: 1. Внутри интервала (b-a) выбираются две точки u11 = a+(3-5)(b-a)/2 и u12 = b-(3-5)(b-a)/2 . 2. Вычисляются Q(u11) и Q(u12). 3. Определяются границы нового интервала a1 и b1. Если Q=Q(u) max, то при Q(u11) > Q(u12) выбираем a1 = a, b1 = u12; при Q(u11) Q(u12) выбираем a1 = u11, b1 = b. Если Q=Q(u) min, то при Q(u11) > Q(u12) выбираем a1 = u11, b1 = b; при Q(u11) Q(u12) выбираем a1 = a, b1 = u12; 4. Проверяется условие окончания поиска b1 - a1 . Метод «золотого» сечения Q=Q(u) max(min), a u b Алгоритм поиска (продолжение): 5. Если условие окончания поиска в пункте 4 не выполняется, на интервале (b1 - a1) со стороны, не смежной с меньшим отрезком, от граничной точки откладывается длина меньшего отрезка. 6. Проводится перенумерация точек: - ближайшая к левой границе обозначается u21; - ближайшая к правой границе обозначается u22; 7. Для каждого нового интервала (bi - ai) повторяются пункты 2-6 до выполнения условия bi - ai . Метод с использованием чисел Фибоначчи Q=Q(u) max(min), a u b Q(u) u2 ,23(b a) a 00.23(b-a) u1 b u 0.38(b-a) Поиск с использованием чисел Фибоначчи Метод с использованием чисел Фибоначчи Q=Q(u) max(min), a u b Алгоритм поиска: 1. Определяется число N, N = (b-a)/ . 2. В ряду чисел Фибоначчи находят Fs-1 < N < Fs, где F0 = F1 =1, Fi = Fi-2 + Fi-1 , i = 2,3,4,… 3. Вычисляется = (b-a) / Fs. 4. Выполняется 1-й шаг: u1 = a + *Fs-2 и вычисляется Q = Q(u1). 5. Выполняется 2-й шаг: u2 = a + *Fs-2-1 и вычисляется Q = Q(u2). Метод с использованием чисел Фибоначчи Q=Q(u) max(min), a u b Алгоритм поиска (продолжение): 6. Дальнейшие шаги: ui+1 = ul ± sign(ui – ui-1) sign(Q(ui) - Q(ui-1))* Fs-2-i , где ul - значение u, при котором достигнуто наилучшее значение функции. Знак (+) ставится в задаче Q(u) max, знак (-) ставится в задаче Q(u) min. На каждом шаге вычисляется функция Q(u). Поиск заканчивается после использования числа Фибоначчи F0 , т.е. когда будут исчерпаны все числа Фибоначчи от Fs-2 до F0 . Численные методы решения многомерных задач статической оптимизации Решается задача Q(u1,…,ur) max(min) u Q(u1*,u2* ) u1* u1 u2* u2 Многомерная функция Численные методы решения многомерных задач статической оптимизации Q(u1*,u2*) u1U1 U u22 Формирование линий уровня многомерной функции Рассматриваются методы: Гаусса-Зейделя, градиента, наискорейшего спуска (подъема), случайного поиска.. Метод Гаусса-Зейделя Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. u2 u1 u1 Поиск методом Гаусса-Зейделя. Метод Гаусса-Зейделя Q(u1,…,ur)max(min) u Алгоритм поиска (заданы i, ): 1. Выбирается исходная точка поиска u1 = (u11, …,u1r) и вычисляется Q = Q(u1). 2. Из точки u1 осуществляется движение по переменной u1 u21 = u11 h1 (sign (Q)/( u1)|u=u ) до выполнения условия |Q / u1| 1. 3. Пункт 2 повторяется из полученной точки для переменной u2. Аналогично осуществляется движение по всем оставшимся переменным u3,u4,…, ur. 4. Проверяется выполнение условия окончания поиска 1 r ( Q / ui ) 2 . i 1 5. В случае невыполнения пункта 4 повторяются пункты 1-4, принимая за исходную точку поиска ту, в которую пришли в пункте 4. Метод градиента Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. Градиент функции Q(u): r Grad Q( u) u K i i 1 Q(u) u, ui где Ki - вектор, определяющий направление по iой координатной оси. 2 r Q( u) Grad Q ( u ) . Модуль градиента u u i 1 ui Направление градиента cos j Q ( u ) / u j Grad Q ( u) u, j 1,..., r. Метод градиента Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. u2 u1 u1 Поиск методом градиента. Метод градиента Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. Алгоритм поиска (задано ): 1. Выбирается исходная точка поиска u1 = (u11, …,u1r) r Q( u) 2 . u1 2. Вычисляется Grad Q(u) u1 i 1 ui 3. Проверяется выполнение условия окончания поиска GradQ( u k ) . 4. Если условие окончания поиска выполнено, то поиск окончен. 5. Если условие окончания поиска не выполнено, то выполняется шаг uk+1i = uki hk cos j в направлении градиента, где знак (+) для задачи Q(u) max, знак (-) для задачи Q(u) min. Метод градиента Алгоритм поиска (продолжение): cos i u k Q ( u) / ui r uk , i 1,..., r. (Q(u) / ui ) 2 j 1 k Если h k h0 GradQ(u ) , то uk+1i = uki h0(Q(u)/ ui)|uk , где h0 – базовое значение шага. 6. Сравниваются значения функций Q(uk) и Q(uk+1). Если для Q(u) max выполняется Q(uk+1) > Q(uk), или для Q(u) min выполняется Q(uk+1) < Q(uk), то пункты 2-6 повторяются до выполнения условия окончания поиска в пункте 3. Если для Q(u) max имеет место Q(uk+1) Q(uk), или для Q(u) min имеет место Q(uk+1) Q(uk), то возвращаются в точку u = uk, уменьшают шаг h0 и переходят к пункту 5. Метод наискорейшего спуска (подъема). Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. u2 u1 u1 Поиск методом наискорейшего спуска Отличается от метода градиента, тем, что движение из выбранной точки uk в направлении n градиента производится до выполнения условия Q ( u) ui uk Q ( u) ui uk i , i = 1,…,r. Метод движения по дну оврага Решается задача Q(u1,…,ur) max(min), u uimin ui uimax, i = 1,…,r. u2 u7 u8 u5 u6 u4 u2 u3 u1 u1 Поиск методом движения по дну оврага Метод движения по дну оврага Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Алгоритм поиска: 1. Задается hmin. 2. Выбор исходной точки поиска u1 и спуск из нее в направлении GradQ(u1) на дно оврага в точку u2. 3. Смещение из точки u1 в точку u3 на небольшое расстояние ортогонально направлению GradQ(u1) и спуск из нее в направлении GradQ(u3) на дно оврага в точку u4. 4. Сравнение значений функций Q(u2) и Q(u4) в точках u2 и u4, лежащих на дне оврага. 5. Если для Q(u) max имеет место Q(u4) Q(u2), или для Q(u) min имеет место Q(u4) < Q(u2), то в направлении от u2 к u4 из u4 выполняется рабочий шаг h и переход в точку u5, лежащую на склоне оврага (хребта). Метод движения по дну оврага Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Алгоритм поиска (продолжение): 6. Спуск на дно оврага из точки u5 в точку u6. Все точки, лежащие на дне оврага, имеют четные индексы и обозначаются u2+2i (i = 0,1,2,…). Все точки, лежащие на склоне оврага (хребта), имеют нечетные индексы и обозначаются u3+2i (i = 0,1,2,…). 7. Сравнение значений функций в соседних точках u2+2i и u2+2(i+1), лежащих на дне оврага. 8. Если для Q(u) max имеет место Q(u2+2(i+1)) > Q(u2+2i ), или для Q(u) min имеет место Q(u2+2(i+1)) < Q(u2+2i), то в направлении от u2+2i к u2+2(i+1) из u2+2(i+1) выполняется рабочий шаг h и переход в точку u3+2(i+1) , лежащую на склоне оврага (хребта). Метод движения по дну оврага Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Алгоритм поиска (окончание): 9. Если для Q(u) max (или Q(u) min) имеет место Q(u2+2(i+1)) Q(u2+2i ) (соответственно Q(u2+2(i+1)) Q(u2+2i), то выполняется возвращение в точку u3+2i и уменьшение рабочего шага h, например вдвое. 10. Проверяется выполнение условия h hmin. 11. Если условие окончания поиска выполнено, то оптимальное значение u* полагается равным u2+2i. 12. Если условие окончания поиска не выполнено, то движение из точки u2+2i с полученным шагом по направлению от u2+2(i-1) к u2+2i и переход в точку u3+2i, а из нее спуск на дно оврага в точку u2+2(i+1). 13. Переход к пункту 7. Решение задач оптимизации на условный экстремум методом штрафных функций Решение задач оптимизации при условии типа равенства Решается задача Q(u) = Q(u1,…,ur) max(min), j(u1,…,ur) = 0, j = 1,…,m. u Формируется штрафная функция (u) Q(u) H (u), m где H (u) 2j (u), > 0 - большое число, j 1 при котором, за исключением малой окрестности около границ j(u) = 0, должно выполнятся условие Q( u) H ( u) ui ui , i = 1,…,r. Знак (+) принимается для задачи Q(u) min, знак (-) принимается для задачи Q(u) max. Решение задач оптимизации на условный экстремум методом штрафных функций Решение задач оптимизации при условии типа равенства u2 (u1,u2)>0 (u1,u2)=0 ( u1,u2)<0 Q1(u) 1(u) u1 Трансформирование линии уровня при условиях типа равенства Линии уровня функции Q(u) трансформируется в линии уровня функции (u) за счет штрафной составляющей H(u), уплотняясь вдоль границы. Чем больше величина и чем больше нарушаются ограничения, тем линии уровня ближе к границе. Решение задач оптимизации на условный экстремум методом штрафных функций Решение задач оптимизации при условии типа неравенства Решается задача Q(u) = Q(u1,…,ur) max(min), u j(u1,…,ur) 0, j = 1,…,m. Формируется штрафная функция r (u) Q(u) (1 sign j (u)) j (u) , где j 1 sign(u) = -1, если j(u) < 0, sign(u) = -1, если j(u) > 0, - большое положительное число. Знак (+) принимается для задачи Q(u) min, знак (-) принимается для задачи Q(u) max. Решение задач оптимизации на условный экстремум методом штрафных функций Решение задач оптимизации при условии типа неравенства u2 u1 (u1,u2)>0 (u1,u2)<0 Q(u) (u) (u1,u2)=0 u1 Трансформирование линии уровня при условиях типа неравенства Линии уровня функции Q(u) трансформируется в линии уровня функции (u) за счет штрафной составляющей m (1 sign j ( u)) j ( u), уплотняясь со стороны j 1 запретной области вдоль границ j(u) = 0, j = 1,…,m. Чем больше коэффициент и чем сильнее нарушаются ограничения, тем плотнее линии уровня функции (u) приближаются к границе со стороны запретной области. Методы случайного поиска Решается задача Q(u1,…,ur)max(min), u uimin ui uimax, i = 1,…,r. Рассмотрим: - метод слепого поиска - метод случайных направлений Метод слепого поиска Q(u1,…,ur)max(min), u uimin ui uimax, i = 1,…,r. Заданы: объем области v = r, определяющей точность вычисления вектора оптимальных управлений u*=(u1,…,ur), в допустимой области изменения переменных ui, (i=1,…,r) объемом V = 1; вероятность , с которой требуется попасть в область r расположения вектора u*. Метод слепого поиска Q(u1,…,ur)max(min), u uimin ui uimax, i = 1,…,r. Алгоритм метода: 1. Вычисляется число точек s в области допустимых значений ui, (i=1,…,r), при котором гарантируется попадание хотя бы одной из них в область v. Из выражения = 1-(1-v)s имеем s = ln(1-) / ln(1-v). 2. Выбираются s совокупностей случайных чисел ui, (i=1,…,r), определяющих uk, (k=1,…,s). 3. Вычисляются значения функции Q = Q(uk), (k=1,…,s) и выбирается наилучшее из них. Метод случайных направлений Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Формируется вектор случайных направлений = (1,…,r), где i i / i, j - случайные числа. r 2 j j 1 u2 u1 u1 Поиск методом случайных направлений , Метод случайных направлений Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Алгоритм поиска: 1. Задаются hmin и число S неудачных направлений из одной точки. 2. Выбирается исходная точка поиска u1 и вычисляется Q = Q(u1). 3. Из выбранной точки выполняется шаг hk в случайном направлении uk+1i = uki + hk·i , i = 1,…,r, и вычисляется Q = Q(uk+1) (для 1-го шага k=1). 4. Сравниваются значения функций Q(uk) и Q(uk+1). Метод случайных направлений Решается задача Q(u1,…,ur) max(min), uimin ui uimax, i = 1,…,r. u Алгоритм поиска (продолжение): 5. Если для Q(u) max имеет место Q(uk+1) > Q(uk), или для Q(u) min имеет место Q(uk+1) < Q(uk), то для точки uk+1 выполняются пункты 3-4. 6. Если для Q(u) max имеет место Q(uk+1) Q(uk), или для Q(u) min имеет место Q(uk+1) Q(uk), то возвращение в точку uk. 7. Проверяется выполнение условия окончания поиска s S, при h hmin , где s - число неудачных направлений из точки uk. 8. Если условие пункта 7 выполняется, то оптимальное u* = uk. 9. Если условие пункта 7 не выполняется, то длина последнего шага уменьшается, например, вдвое, и для точки u = uk выполняются пункты 3-9. Динамическое программирование в дискретной форме В дискретной форме динамическое программирование является декомпозиционным методом решения задач статической оптимизации. Особенность динамического программирования в дискретной форме позволяет свести задачу большой размерности к ряду подзадач меньшой размерности. В динамическом программировании критерий оптимальности Q = Q(u1,…,ur) должен быть функцией Марковского типа, т.е. он может быть представлен в виде функции от состояния S = S (u1,…,ur-1), в которое приходит последний объект в результате воздействия (r-1) управлений, и от оставшегося управления ur, т.е. Q = Q(S, ur). Предполагается, что процесс протекающий в исследуемом объекте, можно рассматривать как многостадийный (N-стадийный, см. рисунок ниже). Динамическое программирование в дискретной форме ( S0,,U ) qq11(S 0 u11) S0 1 U u11 ,U N )1)q q(SN (S N, u1,)U N ) qqN-1 N (S 1( SN-2 N ,1u N-1 N N-1 N (S11,,U qq22(S u22)) S1 2 U u22 S2 SN 2 N-1 S N 1 U N 1 uN-1 N SN UuN N Многостадийный процесс Здесь: Si-1 - состояние перед i-ой стадией; ui - управление на i-ой стадии; qi(Si-1, ui) - составляющая критерия оптимальности, полученная на i-ой стадии. Состояния соседних стадий связаны выражением Si = Si (Si-1, ui), i=1,…,N. Динамическое программирование в дискретной форме Рассматривается критерий оптимальности в N виде Q qi ( Si 1, ui ). i 1 В основе динамического программирования лежит принцип оптимальности: оптимальная стратегия обладает таким свойством, что для любых значений управлений u1,…,uk, при которых система пришла в состояние Sk = Sk (S0, u1,…,uk), оставшиеся управления uk+1,…,ur должны принимать такие значения, при которых критерий оптимальности принимает наилучшее значения относительно состояния Sk. Динамическое программирование в дискретной форме Алгоритм решения задачи оптимизации методом динамического программирования. Принцип оптимальности реализуется по шагам следующим образом: 1. Задаются условно значения вектора состояний Si = (S1i,…, Sin), i=1,…,N-1. Составляющие Sik, i=1,…,N-1; k=1,…,n, есть значения переменных состояния, выбранные в допустимом диапазоне изменения Sikmin Sik Sikmax. 2. На первом шаге оптимизируется N-ая составляющая критерия оптимальности. При решении задачи Q(u)max получаем FN-1,N (Sn-1)=max [qN (SN-1, uN)]. При этом получается u*N = N (SN-1). Динамическое программирование в дискретной форме Алгоритм решения задачи оптимизации методом динамического программирования (продолжение): На втором шаге оптимизируется совместное функционирование N-1-ой и N-ой стадий процесса, с учетом результата оптимизации, полученного на 1-ом шаге, в виде FN-2,N(sN-2)=max[qN-1(sN-2, uN-1)+FN-1,N(sN-1)]. При этом получается u*N-1 = N-1(sN-2). Заметим, что в состоянии sN-1 приходят в соответствии с sN-1= sN-1(sN-2, uN-1). 3. На последующих шагах оптимизируется совместное функционирование вновь вводимой стадии процесса со стадиями процесса, рассмотренными на предыдущем шаге по функциональному уравнению динамического программирования FN-k-1,N (sN-k-1) = = max[qN-k(sN- k-1, uN- k)+FN-k,N(sN-k)], k=2,3,4,…,N. Динамическое программирование в дискретной форме Алгоритм решения задачи оптимизации методом динамического программирования (продолжение): При этом получается u*N-k = N-k(sN-k-1) , а в состояние sN-k приходят в соответствии с sN-k= sN-k(sN-k-1, uN-k). 4. На последнем (N-ом) шаге имеем F0,N (s0) = = max[q1(s0, u1)+F1,N(s1)], u*1 = 1(s0), s1 = s1(s0, u1). 5. Выделяются оптимальные значения управлений u*i, i=1,…,N, следующим образом: Динамическое программирование в дискретной форме Алгоритм решения задачи оптимизации методом динамического программирования (окончание): Для заданного состояния s0 после выполнения N-го шага оптимизации при u*1 = 1(s0) переходят в оптимальное состояние s*1 = s1(s0, u*1). Далее используется выражение u*2 = 2(s*1). Оптимальные значения остальных управлений u*i, i=3,4,…,N выделяются поочередным использованием выражений s*k = sk(s*k-1, u*k) и u*k+1 = k+1(s*k), k=2,3,…N.