- Сайт pta-fiz!
реклама

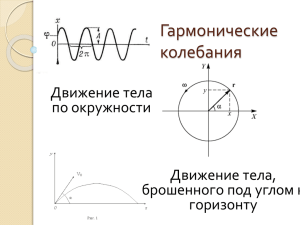
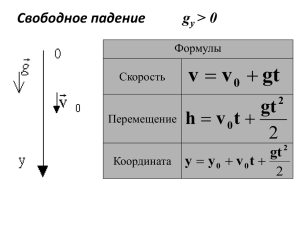
ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ И БРОШЕННОГО ГОРИЗОНТАЛЬНО С НЕКОТОРОЙ ВЫСОТЫ Движение тела, брошенного горизонтально с некоторой высоты, можно разложить на два независимых движения: равномерное прямолинейное, происходящее в горизонтальном направлении со скоростью vx, равной начальной скорости бросания 𝑣0 (𝑣𝑥 = 𝑣0 ) и свободное падение с высоты, на которой находилось тело в момент бросания, с ускорением g. Для описания этого движения выбирают прямоугольную систему координат ХОУ. Траекторией движения является ветвь параболы. Уравнения движений по осям Ох и Оу: 0x: x= 𝑥0 + 𝜐0 t 𝑔𝑡 2 0y: y= 𝑦0 2 Скорость тела в любой точке траектории можно определить по формуле: 𝑣 = √𝑣𝑥2 − 𝑣𝑦2 Движение тела, брошенного под углом к горизонту, можно разложить на два независимых движения: равномерное прямолинейное, происходящее в горизонтальном направлении с начальной скоростью 𝑣0𝑥 = 𝑣0 𝑐𝑜𝑠 𝛼 и свободное падение с начальной скоростью 𝑣0𝑦 = 𝑣0 𝑠𝑖𝑛 𝛼, где α — угол между направлениями вектора скорости 𝑣0 и осью Ох. Траекторией такого движения является парабола. Уравнения движений примут вид: 0x: x=𝑥0 + 𝜐0 t 𝑔𝑡 2 0y: y= 𝑦0 + 𝜐0𝑦 t 2 Скорость тела в любой точке траектории: 𝑣 = √𝑣𝑥2 − 𝑣𝑦2 , где 𝑣𝑥 = 𝑣0𝑥 , 𝑣𝑦 = 𝑣0𝑦 − 𝑔𝑡 Формулы высоты, дальности и времени полета получены с помощью проекций уравнений движения на оси Ох и Оу, с учетом выбора направления осей координат. Найдем траекторию тела, брошенного под углом к горизонту, при условии, что на всем пути его движения ускорение свободного падения остается постоянным. Пусть тело брошено из точки О с начальной скоростью 𝑣⃗0 под углом α к горизонту (рис. 1.35). Выберем оси координат так, чтобы векторы 𝑣⃗0 и 𝑔⃗ были расположены в какой-либо координатной плоскости, например в плоскости ХОY. Ось ОХ направим горизонтально, а ось ОY - вертикально вверх. Начало координат выберем в точке бросания – точке О. Так как ускорение свободного падения с течением времени не меняется (g = 9,8 м/c2), то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями 𝑎𝑦 𝑡 2 𝑎 𝑡2 x = 𝑥0 + 𝜐0𝑥 t + 𝑥 (1.1) y = 𝑦0 + 𝜐0𝑦 t + (1.2) 2 2 При выбранном начале координат x0=0 и y0=0. Проекцию вектора на какуюлибо ось можно выразить через модуль вектора и косинус угла, который этот вектор образует с положительным направлением оси. 𝒗 cos 𝛼 − отношение прилежащего катета к гипотенузе, cos 𝑎 = 𝟎𝒙 𝒗𝟎 sin 𝛼 − отношение противолежащего катета к гипотенузе , sin 𝑎 = Относительно оси 0Х тело движется равномерно: 𝑙 = 𝑆𝑥 = х0 + 𝜐0𝑥 t + т.е. 𝒍 = 𝒙𝟎 + 𝝊𝟎𝒙 𝒕, 𝑎𝑥 𝑡 2 2 𝒗𝟎𝒚 𝒗𝟎 𝑎𝑥 = 0, но х 0 = 0, 𝑙 = 𝑣𝑜𝑥 𝑡 Относительно оси 0У тело движется ускорено с ускорением свободного падения g: ℎ = 𝑦 − 𝑦0 = 𝑦0 + 𝜐0𝑦 t + 𝑔𝑦 𝑡 2 2 𝒈𝒚 𝒕𝟐 𝒚 = 𝒚𝟎 + 𝝊𝟎𝒚 t + 𝟐 Из рисунка видно, что 𝑣0𝑥 = 𝑣0 cos 𝛼, 𝑣0у = 𝑣0 cos(90° − 𝛼) = 𝑣0 sin 𝛼, 𝑎𝑥 = 0, 𝑎𝑦 = −𝑔 Поэтому уравнения (1.1) и (1.2) можно записать в виде: 𝑦 = 𝜐0𝑦 t + 𝑔𝑦 𝑡 2 2 𝑦0 = 0 𝒈𝒕𝟐 𝑥 = 𝑣0 cos 𝛼 ∗ 𝑡 (1.3) 𝒚 = 𝒗𝟎 𝐬𝐢𝐧 𝜶 ∗ 𝒕 − (1.4) 𝟐 Для построения траектории тела можно найти значения координат х и у из уравнений (1.3) и (1.4) для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией. Но траекторию тела можно найти и по-другому. Довольно несложный расчет позволит нам получить уравнение, устанавливающее зависимость между координатами х и у. Такое уравнение называется уравнением траектории. Чтобы получить уравнение траектории, нужно из уравнений (1.3) и (1.4) исключить время. 𝑥 Из уравнения (1.3) имеем 𝑡 = . Следовательно, 𝑣0 cos 𝛼 Пусть 𝐭𝐠 𝒂 = с 𝒈𝒚 𝒙𝟐 𝒙 𝒚 = 𝒗𝟎 𝐬𝐢𝐧 𝒂 ∗ + 𝒗𝟎 ∗ 𝐜𝐨𝐬 𝒂 𝒗𝟎 𝟐 ∗ 𝐜𝐨𝐬𝟐 𝒂 ∗ 𝟐 𝒈𝒚 𝒗𝟎 𝐬𝐢𝐧 𝒂 = ∗𝒙+ 𝟐 ∗ 𝒙𝟐 = 𝟐 𝒗𝟎 𝐜𝐨𝐬 𝒂 𝒗𝟎 ∗ 𝐜𝐨𝐬 𝒂 ∗ 𝟐 𝒈 = 𝐭𝐠 𝒂 ∗ 𝒙 − 𝟐 ∗ 𝒙𝟐 𝟐 𝒗𝟎 ∗ 𝐜𝐨𝐬 𝒂 ∗ 𝟐 − 𝒈 𝒗𝟎 𝟐 ∗𝐜𝐨𝐬 𝟐 𝒂∗𝟐 = 𝒃 , тогда 𝒚 = с𝒙 + 𝒃𝒙𝟐 - квадратичная функция, графиком которой является парабола. Тогда 𝑦 = 𝑏𝑥 2 + 𝑐𝑥 (1.5) Из курса алгебры известно, что графиком функции (1.5) является парабола, ось симметрии которой - прямая, параллельная оси Y. Поскольку в данном случае b<0, то ветви параболы направлены вниз. На рисунке 1.36 изображена парабола для случая b = - 0,2 м-1 и с =1,6. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе. Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально. Из рисунка 1.36 видно, что, начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой находится в точке бросания (рис.1.37). Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте (рис.1. 38). Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струей экран с заранее вычерченной параболой. При определенной скорости истечения воды струя будет располагаться вдоль вычерченной параболы.