ЛАБОРАТОРНАЯ РАБОТА №1 В.Н. Демидов
реклама

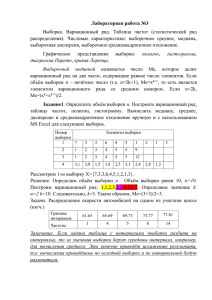
ЛАБОРАТОРНАЯ РАБОТА №1 В.Н. Демидов Тема работы: Анализ эмпирических распределений. Числовые характеристики выборки. Цель работы: Научиться выполнять группировку данных и оформлять результаты обработки эмпирической выборки графически (в виде полигона, гистограммы, эмпирической функции распределения). Научиться вычислять числовые характеристики выборки (показатели положения, разброса, асимметрии), используя приведенные формулы и встроенные функции системы Mathcad. Задание: По заданной эмпирической выборке оценить плотность распределения вероятностей и функцию распределения генеральной совокупности, т.е. построить гистограмму, полигон, эмпирическую функцию распределения и полигон накопленных частот. Сравнить (изобразив на одном графике) эмпирическое и указанное в задании теоретическое распределения вероятностей. Используя функцию Колмогорова, построить 95%-ную доверительную область («полосу») для функции распределения. Вычислить выборочные характеристики (среднее, медиану, моду, дисперсию, стандартное отклонение, коэффициент асимметрии, эксцесс). Сравнить вычисления по приведенным в теоретическом описании формулам и встроенным функциям пакета Mathcad. Теоретическая часть Построение эмпирических распределений. Оценка плотности вероятностей и функции распределения Просматривая результаты наблюдений (измерений) трудно заметить какую-либо закономерность в их изменении. Выявить такие закономерности позволяют статистические методы. Предварительная статистическая обработка опытных данных начинается обычно с того, что их располагают в порядке возрастания (неубывания). Упорядоченная таким образом выборка называется вариационным рядом, а сама процедура упорядочения – ранжированием (или сортировкой) опытных данных. Наглядной формой графического представления эмпирических данных является гистограмма и полигон. При непрерывном распределении случайной величины X эмпирическая плотность распределения вероятностей может быть изображена в виде гистограммы или полигона относительных частот. Для этого должна быть выполнена группировка значений выборки, которая состоит в следующем. Весь интервал x min , xmax , в котором заключены элементы выборки, разбивается на ряд частичных интервалов ai ,bi длины h и подсчитывается число элементов выборки ni , попавших в i -й интервал i 1,2,,m . Параллельно вычисляется и относительная частота wi ni / n . При графическом изображении гистограммы и полигона каждый интервал удобнее представлять не двумя границами ai и bi , а одним значением xi ai h / 2 серединой интервала. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h , а высоты равны отношению ni / h (плотность частоты). Площадь частичного i -го прямоугольника равна hni / h ni - числу выборочных элементов, попавших в i -й интервал. Площадь гистограммы частот равна объему выборки n . Полигон частот – это ломаная линия, получающаяся при соединении точек с координатами xi , ni / h , т.е. соединяются середины верхних сторон прямоугольников гистограммы. Аналогично определяется гистограмма и полигон относительных частот. Для гистограммы относительных частот площадь частичного i -го прямоугольника равна hwi / h wi -относительной частоте элементов, попавших в i -й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице. Полигон относительных частот – это ломаная линия, соединяющая точки x1 ,w1 / h , x2 ,w2 / h ,…, xm ,wm / h , где xi - середины интервалов группировки, wi соответствующие им относительные частоты. Полигон накопленных частот – это график ломаной линии, соединяющей точки k m i 1 i 1 b1 ,n1 , b2 ,n1 n2 , … , bk , ni , … , bm , ni , c абсциссами, равными правым границам интервалов группировки, и ординатами, равными накопленным частотам. Аналогично, полигон накопленных относительных частот – это ломаная линия, получающаяся соединением точек с координатами n1 n1 n2 b1 , , b2 , , … , n n 1 bk , n k i 1 ni , … , bm , 1 n m i 1 ni 1 . В математической статистике доказывается, что гистограмма и полигон относительных частот являются состоятельными оценками плотности распределения, а полигон накопленных относительных частот (или эмпирическая функция распределения) – состоятельной оценкой истинной функции распределения генеральной совокупности. При этом, чем больше объем выборки, тем мельче можно взять интервалы разбиения h и тем точнее гистограмма и эмпирическая функция распределения будут аппроксимировать соответствующие теоретические распределения. Число интервалов группировки эмпирических данных m существенно влияет на вид гистограммы. Четких рекомендаций на этот счет не существует, ясно лишь то, что это число не должно быть «очень малым» или «очень большим». В зависимости от объема выборки число интервалов обычно выбирают в диапазоне 8 – 20. Иногда для выбора m рекомендуется формула m 1 3.32 lg n 1 1.44 lnn , записанная с использованием десятичного или натурального логарифма, или формула m 5 lnn, где n - объем выборки. Эти формулы дают лишь ориентировочное количество интервалов, которое может быть изменено в ту или другую сторону. После определения m вычисляется длина интервалов группировки h x m ax x m in . m Доверительная область для функции распределения, соответствующая уровню доверия p 1 , определяется неравенствами z z Fn x F x Fn x . n n Эти неравенства выполняются сразу для всех x с вероятностью, близкой к p 1 . Данный результат следует из теоремы Колмогорова А.Н., доказываемой в курсе теории вероятностей. Здесь z - корень уравнения (1) K z 1 , а K z - функция (распределения) Колмогорова, определяемая абсолютно сходящимся функциональным рядом z 0 1 K z 1 2 n 1 exp 2n 2 z 2 . (2) n 1 Этот ряд сходится крайне неравномерно, поэтому для достижения одной и той же точности при различных значениях z приходится сохранять различное количество членов ряда (2). Оценки показывают следующее. Чтобы обеспечить точность вычисления функции K z порядка 10-6 в окрестности точки z 1 достаточно сохранить три члена ряда, при z 0.1 уже около 30 членов, а при z 0.001 около 2700 членов ряда. Таким образом, когда z 0 , количество членов рада растет пропорционально z 1 . Но поскольку нас интересует только решение уравнения (1) при малых значениях , когда K z 1 и z 1 , функцию (2) для наших целей можно записать в виде 3 1 K z 1 2 n 1 exp 2n 2 z 2 , (3) n 1 сохранив в сумме всего три слагаемых. Вычисление эмпирических параметров Числовые характеристики выборки вычисляются по следующим формулам: - эмпирическое (выборочное) среднее 1 x n n x ; (4) i i 1 - выборочная дисперсия 1 S n 2 n x x 2 i i 1 1 n n x 2 i 1 s n 1 x , или 2 2 i 1 n x x 2 i ; (5) i 1 - стандартное отклонение 1 S n n x x 2 i , i 1 - размах выборки или 1 s n 1 n x x 2 i ; (6) i 1 R xmax xmin ; (7) - эмпирический центральный момент k -го порядка 1 k n n i 1 xi x , или k 1 n 1 k n k x x ; i (8) i 1 - эмпирические коэффициенты асимметрии и эксцесса 3 A 3/ 2 , 2 4 E 2 3. 2 Несмещенные оценки коэффициентов асимметрии и эксцесса вычисляются по формулам: (9) A nn 1M 4 3n 1M 22 , E n 1n 2n 3s 4 nM 3 , n 1n 2s 3 (10) где n Mk x x , k i k 2 ,3,4 i 1 Вторая формула (5) дает несмещенную оценку дисперсии s 2 , но, несмотря на это, после извлечения квадратного корня (формула (6)) получается смещенная оценка для среднеквадратичного отклонения. Несмещенная оценка вычисляется по формуле Cn s , n 1 n 1 2 , C n 2 n 2 (11) где u - гамма-функция Эйлера. Использовать эту формулу имеет смысл лишь при относительно малом объеме выборки, поскольку множитель C n при больших значениях n приблизительно равен единице: C5 1.064 ; C10 1.028 ; C50 1.005; C200 1.001. Отметим, что оценки математического ожидания и дисперсии x и s 2 являются несмещенными оценками при произвольных распределениях, оценка стандартного отклонения (11) может быть смещенной при распределениях, отличных от нормального распределения. Порядок выполнения задания 1. Присвойте переменной ORIGIN значение равное единице, а переменной n - указанное в задании число, равное количеству элементов эмпирической выборки. 2. Введите (с использованием функции READPRN(“путь к файлу”)) вектор выборочных значений. 3. Выполните операцию ранжирования выборки. 4. Вычислите размах выборки. 5. Задайте (или вычислите) число m интервалов группировки данных. 6. Вычислите характеристики интервалов группировки: h , ai , bi , xi . 7. Определите (с помощью функции hist(x,X)) вектор частот для интервалов группировки. 8. Постройте гистограмму и полигон относительных частот, используя различные стили графического оформления результатов. 9. Определите вектор относительных накопленных частот. 10. Постройте полигон относительных накопленных частот. 11. Сравните эмпирическое и теоретическое распределения (изобразив на одном графике эмпирические полигоны частот и указанное в задании распределение). 12. Поделайте все вычисления для нескольких различных значений m ; сравните результаты. 13. Вычислите все указанные в задании числовые характеристики выборки с использованием формул (4) – (11) и встроенных функций Mathcad. Сравните результаты вычислений. 14. Сохраните рабочий документ. Справочная информация