Показательная функция
реклама
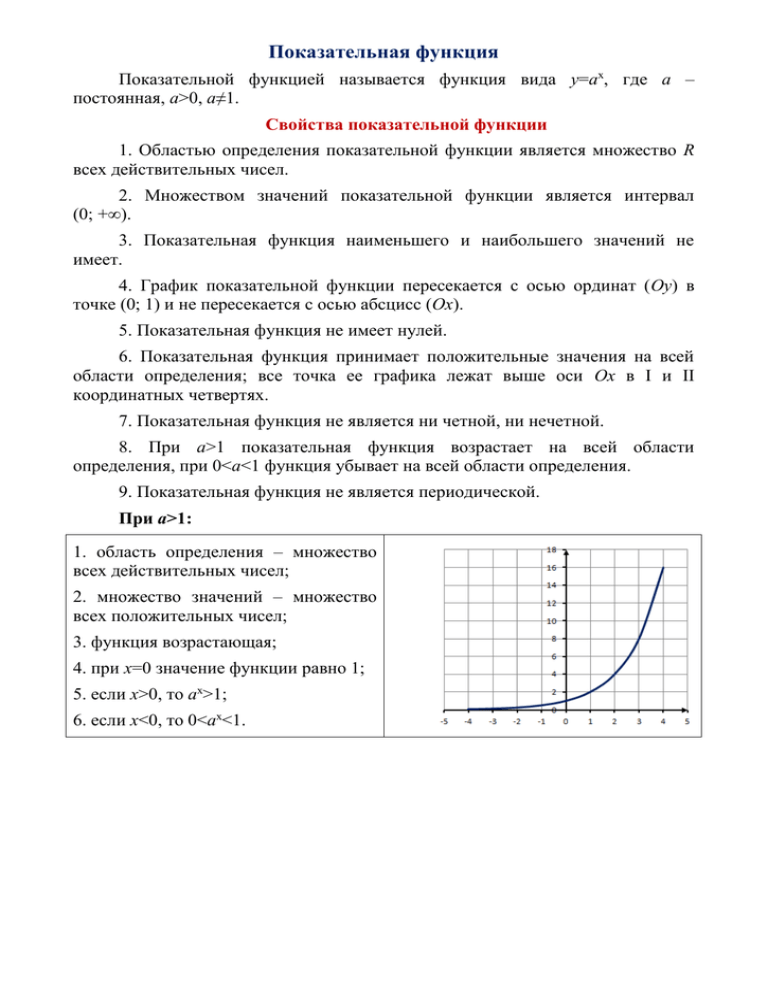
Показательная функция Показательной функцией называется функция вида у=ах, где а – постоянная, a>0, a≠1. Свойства показательной функции 1. Областью определения показательной функции является множество R всех действительных чисел. 2. Множеством значений показательной функции является интервал (0; +∞). 3. Показательная функция наименьшего и наибольшего значений не имеет. 4. График показательной функции пересекается с осью ординат (Оу) в точке (0; 1) и не пересекается с осью абсцисс (Ох). 5. Показательная функция не имеет нулей. 6. Показательная функция принимает положительные значения на всей области определения; все точка ее графика лежат выше оси Ох в I и II координатных четвертях. 7. Показательная функция не является ни четной, ни нечетной. 8. При а>1 показательная функция возрастает на всей области определения, при 0<a<1 функция убывает на всей области определения. 9. Показательная функция не является периодической. При a>1: 1. область определения – множество всех действительных чисел; 2. множество значений – множество всех положительных чисел; 3. функция возрастающая; 4. при х=0 значение функции равно 1; 5. если x>0, то ax>1; 6. если х<0, то 0<ax<1. При 0<a<1: 1. область определения – множество всех действительных чисел; 2. множество значений – множество всех положительных чисел; 3. функция убывающая; 4. при х=0 значение функции равно 1; 5. если x>0, то 0<ax<1; 6. если х<0, то ax>1. Существует основание показательной функции 2<a<3 такое, что касательная, проведенная в точке (0; 1), образует с осью Ох угол 45о. Это число было открыто еще в XVII веке Джоном Непером и названо неперовым числом. Оно приближенно равно 2,7182818284. С XVIII века неперово число стали обозначать буквой е в честь Леонарда Эйлера. В 1766 году Ламбертом (с помощью Эйлера) было доказано, что число е, как и число π иррационально. е – это число, при котором угловой коэффициент касательной к графику функции у=ех в точке х=0 равен 1. Функцию у=ех часто обозначают у=expх и называют экспонентой. Известно много формул для приближенного вычисления числа е. Самыми 1 1 1 1 распространенными являются формулы 𝑒𝑛 = (1 + )𝑛 , 𝑒𝑛 = 1 + + + + 1 ⋯+ , которые при натуральных n 1∙2∙…∙𝑛 приближенных значений е с любой точностью. 𝑛 дают 1 1∙2 1∙2∙3 последовательности Примеры решения задач Пример 1. Изобразить схематично график функции у=2х. Решение. Так как 2>1, то функция возрастающая. Если х=0, то у=20=1. Пример 2. Изобразить схематически график функции у= -32х. Решение. Так как 2>1, то функция у=2х возрастающая. График у= -32х симметричен относительно оси Ох графику функции у=32х. Пример 3. Изобразить схематически график функции у=3|x -1|. 1 Решение. Пусть х -1≥0 (x>1), тогда у=3|x -1|=3х -1=3х3 -1= 3х. 3 1 1 3 3 Пусть х -1≤0 (x1), тогда у=3|x -1|=3–(х-1)=31-х=3( )х. Здесь <1. Соединив эти графики, получим график функции у=3|x -1|. Упражнения 1. Является ли показательной функция: 1) у=3х 2) у=х2 3) у=( -3)x 4) у=√3𝑥 5) у=x 6) у=(x-2)5 7) у=πx 8) у=5-x 9) у=√𝑥 10) у=x0,1 2. Укажите область значений функции: 1) 2х 2) 0,4х 3) 1х 4) 2x - 2 5) 3 - x 6) 0,65х 7) 3 - 0,4x 8) 3|x| 9) 0x 10) 1x+2 3. Укажите (при а>0) область определения выражения: 1) а3х 2) а√х 6) asinx 7) а√16−𝑥 1 3) а√х 2 8) а√tgх 4 4) acosx+1 5) а𝑥2−9 9) atgx 10) а√𝑥 2 −64 4. Является ли возрастающей (убывающей) функция: 1) у=4х 2) у=0,5х 3) у=0,2-x 6) у=22x 7) у=√3x 8) у=( ) -x 1 2 4) у=1,4-x 2 9) у=( )-x 3 5) у=67-x/2 3 10) у=( )x 2 5. Укажите координаты точек пересечения графиков: 1) у=7x и у=343 2) у=2х и у=8 3) у=( )x и у=9 3 5) у=2х и у= -3 6) у=2х+2 и у=4 7) у=3х и у= 9) у=3х и у=81 10) у=8 и у=(sin )х 1 1 1 4) у=( )х и у= 4 64 8) у=3 и у=2х+2 1 3 𝜋 6 6. При каком значении а график функции у=ах проходит через точку: 1) А(1; 2) 1 6) K( ; √2) 2 2) В(2; 8) 3) С(2; 16) 7) S(- 2; 8) 4) Р( - 2; 4) 5) T( - 3; 9) D(1; 1) 10) E( - 2; 4) 3) у=( )х 4) у=3,5х 5) у= -2,5х 8) у=17х-1 9) у=3-х 10) y= -2х 8) F(1; - 15) 1 7. Изобразите схематично график функции: 1) у=2х+1 2) у=4х 6) у=2|x|-1 7) у=( )х 1 4 3 4 8. Найдите по графику функции: 1) значение а; 2) область определения; 3) область значений; 4) промежутки возрастания (убывания); 5) координаты пересечения графика с осью ОУ; 6) значение в точках х1= -1 и х2=1; 7) запишите уравнение функции. 1) 2) 3) ) 27 5) 6) 4) 7) 8) 9) 10) 9. Найдите наибольшие и наименьшие значения функций: 1) y=2х, x[ - 1; 1] 2) y=2x+3x, x[ - 1; 0] 3) y=ехsinx, x[0; π] 4) y=4√𝑥 , x[0; 4] 5) y=3 - х, x[0; 2] 6) y=ех, x[0; 2] 7) y=5|х|, x[ - 1; 1] 8) y=x+ex, x[ - 1; 1] 9) y=2cosх, x[0; π] 10) y=2sinх, x[ - π; π] 10. Изобразите схематично график функции: 1) у=|2x| 2) у=|3x -1| 3) у=|3-x| 4) у=3|x|+x 5) у= -|4|x|| 6) у=|2x-1-1| 7) у=4|x| 8) у=5-|x| 9) у= -0,2|x| 10) у=3|x|-x Дополнительные задания 1. Постройте график функции: 1) y= - 5ех 2) y=ехsinx 3) y=e|x| 4) y=e3x 5) y=2ex 6) y=хе - х 7) y=e – xcosx 8) y=esinx 9) y=3e - x 10) y=e - x 2. Найдите производную функции: х 1) y=2ex 2) y=ехsinx 3) y=e - x 4) y=e – xcosx 5) y= 6) y=ех+е - х 7) y=х2e - x 8) y=ех+2х 9) y=5х+1 10) y=3e - x ех Вариант 1 1. Какой из графиков является графиком функции у=2х? 1 2 3 2. Какой из графиков является графиком функции у= - 0,5х? 1 2 3. Определите по графику значение функции в точке х=3. 4. Определите по графику значение аргумента в точке у= - 20. 5. Определите по графику промежутки возрастания и убывания функции. 6. Определите по графику значение а. 7. Определите по графику нули функции. 8. Постройте график функции у=2х+1. 9. Постройте график функции у=25 - 5х. 10. Для предложенного графика запишите функцию: 3 Вариант 2 1. Какой из графиков является графиком функции у=3х? 1 2 3 2. Какой из графиков является графиком функции у=5+2х? 1 2 3. Определите по графику значение функции в точке х= - 4. 4. Определите по графику значение аргумента в точке у=25. 5. Определите по графику промежутки возрастания и убывания функции. 6. Определите по графику значение а. 7. Определите по графику нули функции. 8. Постройте график функции у=3х - 2. 9. Постройте график функции у=3х - 9. 10. Для предложенного графика запишите функцию: 3
