Реализация компетентностного подхода в процессе решения

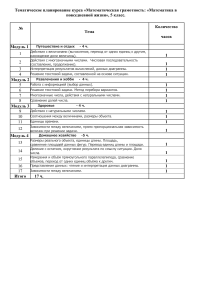
Реализация компетентностного подхода
в процессе решения
математических задач
Заместитель директора
МОУ «Общеобразовательный лицей АМТЭК»
Л.А.Селяничева
Принципы
компетентностного подхода:

смысл образования - развитие у обучаемых способности
самостоятельно решать проблемы в различных сферах и видах
деятельности на основе использования социального опыта, элементом
которого является и собственный опыт обучающихся;

содержание
образования
–
дидактически
адаптированный
социальный опыт решения познавательных, мировоззренческих,
нравственных, политических и иных проблем, достигнутых
обучающимися на определенном этапе обучения;

организация образовательного процесса – создание условий для
формирования у обучаемых опыта самостоятельного решения
познавательных, коммуникативных, организационных, нравственных и
иных проблем, составляющих содержание образования;

оценка образовательных результатов основывается на анализе
уровней образованности, достигнутых учащимися на определенном
этапе обучения.
Вариативные показатели компетенций
обучающихся
Интеллектуальные компетенции:
 наличие потребности учащихся к познавательной деятельности;
 умение ориентироваться и пользоваться различными
информационными источниками для получения новых знаний;
 владение дидактическими умениями и навыками образовательной
деятельности;
 сформированное целостное представление о картине мира, выбор
собственной мировоззренческой позиции;
 умение выявить закономерности, лежащие в основе изучаемых наук,
норм, правил общественной жизни.
Общекультурные компетенции:
 формирование ценностных оснований гуманистического характера;
 умение выявлять, оценивать различные явления действительности с
опорой на ценностные основания;
 глубокое уважение к людям, бережное отношение к национальным
традициям;
 формирование способности действовать в окружающем
микросоциуме в соответствии с этическими и эстетическими
нормами и правилами поведения.
Методологические компетенции:
 умение исследовать, анализировать, классифицировать,
систематизировать, обобщать явления действительности, научные
знания;
владение методами научного познания окружающего мира;
 формирование навыков самоопределения, имеющих значение для
решения проблем в любых видах деятельности;
 умение проектировать и планировать собственную деятельность –
познавательную, социальную, профессиональную;
 развитие рефлексивных способностей, самоанализа, самоконтроля
своих интересов и возможностей.

Коммуникативные компетенции:





знание о средствах, способах, закономерностях общения;
владение средствами предупреждения и разрешения конфликтов в
жизненной ситуации;
знание психологических особенностей личности, законов и
закономерностей личностного развития;
прогнозирование и оценивание последствий развития конфликтных
ситуаций в быту, обществе, школе, в общении со сверстниками;
саморегуляция собственного поведения в рамках норм
коммуникации.
Параметры результативности обучения
математике

общее развитие личности (алгоритмическая деятельность,
логико-дедуктивное мышление, визуально-образное
мышление, математическая речь и символика);

объем научных знаний (предметные знания, широта и
качество знаний, динамика индивидуального усвоения
знаний, глубина знаний в выбранном разделе);

продуктивная деятельность (развитие творческих
способностей, самостоятельность, способность к обобщению,
способность ориентироваться в новой ситуации, прикладная
направленность обучения, способность к моделированию,
исследование результата, самоконтроль).
Диагностика результативности работы
над задачей
1. Определение целей и функций задачи с учетом формируемых
навыков, мыслительных умений, места в курсе, в теме, на уроке;
особенностей учащихся; приобретенных ранее навыков; с учетом
допускаемых ошибок; трудностей, испытываемых учащимися.
2. Принятие цели детьми
3. Учет условий, влияющих на эффективность решения задачи:
• подбор предварительных упражнений;
• привлечение внимания, обеспечение необходимой мотивации;
• оптимальные временные рамки;
• четкая организация работы учителя и учащихся, определение
функций учителя и ученика при решении задачи
4. Процесс работы над задачей:
• выбор этапов решения оптимален для достижения цели;
• используемые учителем методы и приемы в процессе работы
над задачей способствуют продуктивности, активизации учебнопознавательной и учебно-практической деятельности;
• характеристика выводов и логических рассуждений (наличие
обобщений, сравнений, анализа, его глубина);
• подбор наводящих вопросов;
• характер самостоятельности учащихся;
• наличие закрепления;
• приемы
стимулирования
активности,
осуществление
дифференцированного подхода к решению задач;
• специальные способы работы, расчитанные на пассивных
учащихся;
• анализ ситуации;
• используемые приемы контроля, наблюдение за процессом
решения;
• отслеживание, анализ результата, роль учащихся в этом
вопросе, подведение итогов, определение путей коррекции.
5. Оценка деятельности учащихся:
• уровень активности, внимания, работоспособности;
• понимание учащимися материала (наличие вопросов на уточнение,
адекватность ответов, учет активности);
• доля самостоятельности учащихся;
• правильность выполнения действий, демонстрация знаний;
• продуктивность деятельности учащихся.
6. Степень достижения результата в соответствии с поставленной
целью.
Этапы подготовки школьников
к решению задач
1. Обучение анализу условия. Знакомство с понятиями:

Величина. Отношения между величинами. Методы сравнения
однородных величин.

Сравнение и упорядочивание объектов по разным признакам: длине,
массе, вместимости, площади.

Установление зависимостей между величинами, характеризующими
различные процессы. Графическая интерпретация условия (схема,
рисунок, таблица).

Анализ условия. Построение модели.
2. Обучение поиску пути решения, составлению плана решения.
3.
Обучение проверке
правильности.
решения
задачи,
установления
его
Приемы проверки: прикидка ответа, соотношение полученного
результата и условия задачи, решение задачи другим способом,
решение обратной задачи).
Приемы преобразования
учебного материала

Меняется сюжет задачи и (или) числовые значения величин задачи.

Меняются математические зависимости между величинами,
заданными в условии.

Добавляются данные в условии задачи при том же требовании
задачи.

Меняется (добавляется) требование задачи при том же условии.

Составляются обратные задачи.

Составляются задачи с недостающими (избыточными) данными.

Конструируются исследовательские задачи.
Диагностическая карта оценки
сформированности ключевых
компетенций школьника
Ф
И
Работа с
текстом
задачи
умение
читать
текст
задачи
умение
описать
ситуацию
Работа над
условием задачи
умение
анализировать
условие задачи
выде
лять
извес
тные
вели
чины
выде
лять
неиз
вестные
вели
чины
устанавливать
связи
между
вели
чина
ми
умение
записывать
условие в
виде
схемы
черте
жа
Организ Коммуникати
аторские вные умения
умения
Рефлекс
ивные
умения
составлять
план
само
анализ
работать
по
плану
уме
ние
стро
ить
монолог
умение
участ
вовать
в
дискуссии
исполь
зова
ние
термино
логии
само
конт
роль
http://www.eidos.ru
Лебедев О.Е. Управление образовательными
системами. – М., 2004.
Виноградова Л.В. Методика преподавания
математики в средней школе. – Ростов – на –
Дону:Феникс, 2005.
Резанов Р. Формирование компетенции на уроках
математики в 5-8 классах // Звездный опыт. – 2004. №12. – с.45 – 53
Смирнова А.А. Метод варьирования текстовых задач
по математике как средство повышения качества
знаний учащихся: Диссертация канд. пед. наук:
13.00.02/(РГПУ им. А.И.Герцена). СПб., 2007.
Спасибо за внимание