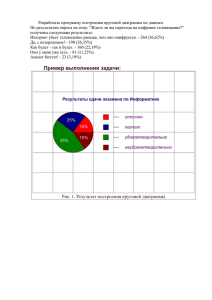
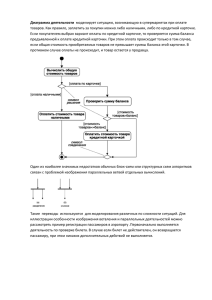
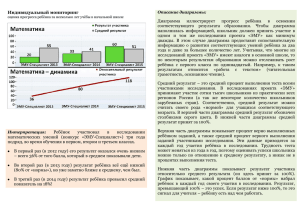
Диаграммы плавкости

ФАЗОВОЕ РАВНОВЕСИЕ
В ДВУХКОМПОНЕНТНЫХ СИСТЕМАХ
ФИЗИЧЕСКАЯ ХИМИЯ. ЛЕКЦИЯ 9.
Фазовые равновесия в двухкомпонентных
системах
Двухкомпонентными называются системы, образованные двумя
компонентами, которые могут быть как простыми веществами, так и
химическими соединениями.
Состояние двухкомпонентной системы может быть охарактеризовано
четырьмя параметрами:




давлением
температурой
содержанием x одного компонента
содержанием (1-х) другого компонента
Правило фаз С=К-Ф+2
В равновесной двухкомпонентной двухфазной системе только два
параметра являются независимыми
С=2-2+2=2
2
Диаграммы двухкомпонентных систем

T=const изотермические диаграммы состояния p-x

p=const изобарные диаграммы состояния Т-x

В конденсированных системах роль давления обычно невелика, в качестве параметров
состояния таких систем выбирают температуру T и состав x (концентрацию одного из
компонентов)
3
Диаграммы плавкости

Такие диаграммы служат для установления условий равновесия между твёрдыми и жидкими фазами
(система т-ж)

Примеры: металлические сплавы, силикаты (стекло), водные растворы солей, системы, состоящие из
органических соединений и т.д.

Диаграммы плавкости – графики, выражающие зависимость температур начала и конца
кристаллизации твёрдого вещества от состава системы

По таким диаграммам можно судить о наличии тех или иных фаз, их числе, температуре
кристаллизации смеси определённого состава и т.д.

Простейшая диаграмма для систем, неограниченно смешивающихся в жидком и не смешивающихся
в твёрдом состоянии – диаграмма с эвтектикой
4
Процесс охлаждения расплава
5
Правило рычага
Состав фаз, находящихся в равновесии,
определяется правилом рычага:
если одна фаза при изменении
параметров системы разлагается на
две другие фазы, то количественное
соотношение образующихся фаз будет
обратно пропорционально длинам
отрезков от точки состава исходной
фазы до точек состава образующихся
фаз
6
Число степеней свободы

Точка m: К=2 (вещества А и В), Ф=1 (жидкая фаза),
С=2-1+1=2, система бивариантна, т.е. можно в
определённых пределах вводить любой из двух
компонентов и изменять температуру – система
будет оставаться гомогенной.

Точка n: К=2 (вещества А и В), Ф=2 (жидкая и
твёрдая фазы), С=2-2+1=1, система
одновариантна, т.е. без изменения числа фаз
можно менять только один параметр – либо
температуру, либо состав смеси.

Точка k: К=2 (вещества А и В), Ф=2 (твёрдое
вещество А и твёрдое вещество В), С=2-2+1=1,
система одновариантна.

Точка Е: К=2 (вещества А и В), Ф=3 (твёрдое
вещество А, твёрдое вещество В и жидкая фаза),
С=2-3+1=0, система безвариантна. Точка Е
характеризуется строго определённым составом
XA и XB, а также температурой TE.
7
Диаграмма плавкости
1-нафтола и трихлоруксусной кислоты
8
Диаграмма плавкости
бензола и нафталина
9
Примеры диаграмм плавкости
10
Диаграмма состояния
трёхкомпонентной системы
11
Охлаждающие смеси
12
Диаграммы растворимости с неограниченной
растворимостью компонентов

Если два компонента неограниченно
растворяются в твёрдом и жидком
состоянии, то возможно существование
только двух фаз – жидкого раствора
(расплава) и твёрдого раствора

Компоненты сплава: компонент А и
компонент В;

Фазы: жидкий раствор Ж и кристаллы
твердого раствора α

Линия С1Д – линия ликвидуса, линия
С2Д – линия солидуса

Число компонентов системы равно
двум, но твёрдый раствор, состоящий из
двух компонентов, образует в твёрдом
виде гомогенную однофазную (Ф=1)
систему
13
Процесс охлаждения расплава
14
Диаграммы кипения

Частный случай диаграммы состояния

Нижняя линия – линия жидкости – показывает
зависимость температуры кипения жидкой
смеси от её состава

Верхняя линия – линия пара – показывает
зависимость температуры конденсации
насыщенного пара от состава паровой смеси

Поле (1) – область пара. В этой области
существует только одна фаза – насыщенный
пар. В каждой точке этой области плотность
системы и другие характеристики одинаковы,
поэтому эта область называется гомогенной.

Поле (2) – область жидкости. В этой области
существует тоже одна фаза, но эта фаза –
жидкость. Область жидкости – тоже
гомогенная область.

Поле (3) - область существования кипящей
жидкой смеси и равновесного с ней пара.
Здесь сосуществуют две фазы. Это
гетерогенная область.
15
В гетерогенной области составы
жидкости и находящегося с ней в
равновесии пара не совпадают с
общим составом!
Правило рычага

Произведение массы жидкой фазы на
плечо, соединяющее точку опоры (а) с
линией жидкости, равно произведению
массы пара, на плечо, соединяющее
точку (а) с линией пара:

Если известна общая масса системы m,
то, используя правило рычага, можно
найти массы сосуществующих фаз.
Выразим массу пара через общую массу
системы и массу жидкости:

Правило рычага в этом случае примет
вид:
Определив по диаграмме размер
отрезков ab и ac, можно найти массу
жидкости, а затем и массу пара в
двухфазной области
Правило рычага используют только в
двухфазной области!
16
Диаграммы кипения неидеальных систем
17
Диаграммы кипения с азеотропными точками
18
Диаграмма кипения
19
T-x, p-x и x-y диаграммы смесей без азеотропа
20
T-x, p-x и x-y диаграммы азеотропных смесей с
минимумом и максимумом температуры кипения
21
Законы Коновалова

1-ый закон: пар обогащается (по
сравнению с жидкостью)
легкокипящим (низкокипящим)
компонентом

2-ой закон: точки максимума и
минимума на кривой общего
давления пара или температуры
кипения отвечают раствору, состав
которого одинаков с составом
равновесного с ним пара

3-ий закон: в изотермических и
изобарных условиях составы
раствора и пара изменяются
симбатно (т.е. между ними есть
устойчивая функциональная связь)
22
Коновалов Дмитрий Петрович
1856-1929
Фазовые диаграммы
частично смешивающихся жидкостей
никотин-вода
метилэтилкетон-вода
анилин-вода
фенол-вода
хлороформ-вода
диметиловый эфирвода
диэтиламин-вода
триэтиламин-вода
ВКТР и НКТР - верхняя и нижняя критическая температура растворения
23