Лекции в формате ppt, 4.22 МБ - Кафедра физики атомного ядра

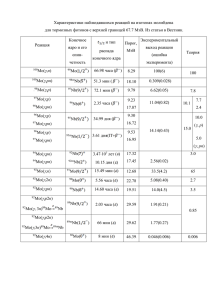
Раздел III. Взаимодействие
-квантов с веществом.
-излучение находится в высокочастотном диапазоне
электромагнитного спектра (см. таблицу). Его источниками
являются радиоактивные распады, ядерные реакции, космические
лучи и т.д. При взаимодействии -квантов с веществом можно
выделить три основных процесса:
(1) фотоэффект;
(2) эффект Комптона;
(3) образование электрон-позитронных пар.
Раздел III.
1. Фотоэффект (ФЭ).
Под фотоэффектом понимают процесс, в
котором электроны испускаются
веществом в результате его облучения
электромагнитным излучением.
Испущенные электроны называют
фотоэлектронами. Различают внешний
фотоэффект (фотоэлектроны покидают
вещество) и внутренний фотоэффект
(фотоэлектроны свободно перемещаются
в веществе, но его не покидают).
История открытия
Александр Беккерель
(Alexandre Edmond Becquerel,
1820 – 1891)
В 1839 г. французский
физик Александр
Беккерель обнаружил
фотогальванический
эффект: он наблюдал
ток, когда освещал
светом электрод,
опущенный в
проводящий раствор.
Уиллоуби Смит
(Willoughby Smith, 1828 – 1891)
В 1873 г. английский
инженер-электрик
Уиллоуби Смит,
работавший
старшим
электриком в
телеграфной
компании, открыл
явление
фотопроводимости
селена.
В 1887 г. немецкий физик
Генрих Герц, выполняя
эксперименты по
генерации и приему
электромагнитных волн,
случайно обнаружил, что
заряженный объект
Генрих Герц
(Heinrich Rudolf Hertz,
1857 – 1894)
«охотней теряет заряд»,
если его облучают
ультрафиолетом.
Филипп Ленард
(Philipp Eduard Anton von Lénárd,
1862 – 1947)
В 1900 г. немецкий физик
Филипп фон Ленард
установил, что
испускаемые заряженные
частицы – электроны
(отсюда название
«фотоэлектрический
эффект»). В 1902 г. он
установил изменение
энергии электронов с
частотой света.
В 1905 г. («год чудес»)
Эйнштейн опубликовал
эвристическую гипотезу о
«световых квантах»
(фотонах) и описал
Альберт Эйнштейн
в 1905 г.
(Albert Einstein,
1879 - 1955)
основные свойства и
закономерности
фотоэффекта.
В 1915 г. американский
физик Роберт Милликэн
экспериментально
подтвердил все
Роберт Милликэн
(Robert Andrews Millikan,
1868 - 1953)
предсказания Эйнштейна
относительно
фотоэффекта.
Нобелевская премия по физике
(1921 г.)
«За заслуги перед Теоретической
Физикой и особенно за открытие закона
фотоэлектрического эффекта»
Альберт Эйнштейн
(Albert Einstein,
1879 - 1955)
Нобелевская премия по физике
(1923 г.)
«За работы по элементарному заряду
электричества и фотоэлектрическому
эффекту»
Роберт Милликэн
(Robert Andrews Millikan,
1868 - 1953)
Интересный факт
Милликэн долго не мог смириться с тем,
что эвристическая гипотеза Эйнштейна
о фотонах оказалась верной, т.к. это
противоречило волновой природе света.
Кроме того, он продолжал верить в
«эфир», даже признавая, что СТО и
ОТО Эйнштейна очень успешно
объясняют «иначе необъяснимые»
явления.
Атомный ФЭ
Фотоэффект на атоме
сопровождается либо ХРИ, либо
Оже-процессом.
E  Te  I K  Tion Tion  Te ,

 
p  pe  pion  pe  pion  p .
Ключевой момент для понимания физики ФЭ:
свободный электрон не может поглотить фотон!
Действительно, записывая законы сохранения энергии и импульса для
процесса поглощения фотона свободным электроном в системе отсчета,
где перед поглощением электрон покоится, получим:
 E  m c 2  c p 2  m 2c 2 ,

e
e
e
 E  0.

 p  pe  p  E c  ,
Ремарка. У каждого правила есть свое исключение. На самом деле
возможна специфическая ситуация, когда свободный электрон может
поглотить фотон – это процесс, обратный процессу черенковского
испускания фотона!
Таким образом, чем слабее связан
электрон в атоме, тем меньше
вероятность ФЭ и наоборот. Значит
можно ожидать, что:
(1) вероятность ФЭ для K-оболочки
больше, чем для L-оболочки и т.д.;
(2) чем больше Z, тем вероятнее
фотоэффект;
(3) с ростом E вероятность ФЭ падает.
σp.e.
IM
IL
IK
E
Рис. Качественный вид зависимости сечения ФЭ от энергии -кванта.
Резкие скачки наблюдаются при энергиях, равных потенциалам
ионизации электронных оболочек атома вещества.
Теория атомного ФЭ
В рамках КЭД можно аналитически вычислить сечение ФЭ для атома
водорода или водородоподобного иона с зарядом Z << 137.
В нерелятивистском случае (E << mec2):
 I
dσ
7
2
 2  a 
E
d
 
 exp  4  arcctg 
2
n

e
 

 1  exp  2 
4

a0
Ze 2 me 
a  ;  
.
Z
pe 

n – направление импульс фотоэлектрона; e – вектор поляризации фотона.
2
9 2
9 2

a
2

2

2
0
Если E  I (т.е. η  ): σ 
a 
.
2
3
3 Z
Если mec2 >> E >> I (т.е. η << 1):
 I
2
2
σ
a 
E
3
 
8



7
2
 I0
2
2 5

 a0 Z 
E
3
 
8



7
2

 2 me c 2 
2
 I  Z I0 ; I0 
.
2 

E=150 эВ; E – вектор поляризации
фотона; kph и ke – импульсы фотона и
электрона.
В ультрарелятивистском случае (E-I >> mec2):
1  β  
1  β   
2
dσ  4 Z  r
5
4 2
e
2
3


e2
d

d

r


2,82
Фм
 e
.
3
2
me c


3
2
2
Таким образом, угловое распределение имеет острый максимум при θ~1/
( - Лоренц-фактор), т.е. фотоэлектроны испускаются преимущественно в
направлении падения фотона. Полное сечение есть
1
σ  2 Z 5 4 re2 .
γ
Отношение сечений фотоэффекта для разных электронных оболочек:
σL 1
 ,
σK 5
σM 1
5

 σ tot   σ X  σ K .
σL 4
4
X
Основные выводы теории ФЭ
• Сечение ФЭ ~ Z5;
• Сечение ФЭ падает с ростом E:
~ (1/E)7/2, если E > IK;
~ 1/E, если E >> IK;
• Сечение ФЭ на 80% определяется ФЭ
на K-оболочке.
Ядерный ФЭ (ЯФЭ)
Под ЯФЭ понимают реакции под действием -
квантов типа (,n), (,p), (,α) и т.п. Впервые ЯФЭ
наблюдался английским физиком Чедвиком и
американским физиком Гольдхабером в 1934 г.:
  d  p  n (Wd  2, 2 МэВ).
Джеймс Чедвик
(James Chadwick, 1891 – 1974)
Морис Гольдхабер
(Maurice Goldhaber, р.1911)
Основные свойства ЯФЭ
•Порог ЯФЭ определяется энергией связи нуклона: E ~ 6-10 Мэв;
•Сечение ЯФЭ ~Z;
•Для легких ядер (A < 100) фотоядерные реакции отщепления
нуклона (нейтрона или протона) идут через составное ядро  угловое
распределение нуклонов изотропно;
•Для тяжелых ядер (A > 100) угловое распределение нейтронов
изотропно (т.е. механизм составного ядра), а протоны вылетают под
углом ~ 90° (механизм составного ядра не работает);
•Относительный выход протонов ~ 10-2 по сравнению с выходом
нейтронов, однако он ~ 100 раз больше, чем предсказывает
боровская теория составного ядра (т.е. работает прямой механизм –
вырывание периферийных протонов).
Реакция
(Е)рез,
МэВ
Г,
МэВ
σmax,
мбарн
19,2
4,7
20
17,5
6,0
108
15,0
6,0
820
13,0
6,0
1800
В области E ~ 10-20 МэВ для всех ядер наблюдается очень широкий
резонанс (Г ~ 3-6 МэВ) в сечении фотопоглощения – гигантский резонанс.
Приближенно экспериментальная зависимость имеет вид: (Е)рез~ A-1/5 МэВ.
Гигантский дипольный резонанс
(ГДР)
В области энергий E ~ 10-20 МэВ длина волны -кванта λ ~ 10-12 см (>> Rя)
 протоны в ядре попадают в электрическое поле волны одинаковой фазы.
Под действием этого поля все протоны смещаются относительно нейтронов
и возникают дипольные колебания. Частота таких колебаний :
где k – коэффициент упругости поверхностных сил, М – масса ядра.
Возникновение поверхностных сил упругости связано с ядерными силами
между «оголенными» протонами и нейтронами вблизи поверхности ядра с
оставшейся частью ядра. Поэтому коэффициент упругости должен быть
пропорционален числу оголенных нуклонов, т.е. поверхности ядра.
Следовательно,
что хорошо согласуется с экспериментальной зависимостью (Е)рез~ A-1/5 МэВ.
Лучшее согласие с экспериментом достигается, если учесть не только
колебания, вызванные действием поверхностных сил, но и линейное
натяжение из-за действия ядерных сил при колебаниях протонов
относительно нейтронов. Очевидно, что подобные колебания должны быть
пропорциональны изменению линейных размеров ядра, т.е. k ~ A1/3.
Поэтому частота линейных колебаний:
Линейная суперпозиция частот
ωрез = аωпов + bωлин
дает хорошее согласие с экспериментальными значениями (Е)рез при
подборе коэффициентов a = 31,2 МэВ и b = 20,6 Мэв.
Дипольное правило сумм для фотопоглощения:
m c 2

0
NZ
σ  Eγ  dEγ  0, 06
б  МэВ
A
2
m
c
   135 МэВ .
Раздел III.
2. Упругое рассеяние -квантов.
Помимо ФЭ возможны процессы
взаимодействия, в которых -квант не
поглощается, а рассеивается. Рассеяние
может быть упругим (т.н. когерентное
рассеяние), либо неупругим
(некогерентным). Упругое рассеяние более
вероятно для длинноволновых фотонов, в
то время как неупругое – для
коротковолновых (например, эффект
Комптона).
Томсоновское рассеяние
Джозеф Томсон
(Joseph John Thomson , 1856 – 1940)
В электромагнитной волне на заряженную частицу действует
периодическая сила Лоренца. Периодически движущийся заряд будет
излучать волны той же частоты. Впервые этот процесс рассеяния
объяснил английский физик Дж.Дж.Томсон.
Если скорость заряда q много меньше скорости света, то можно пренебречь
магнитной составляющей силы Лоренца:
E  E0 cos  k  r  t   a 
F qE0

cos  k  r  t  .
m
m
Интенсивность излучения заряда (в дипольном приближении):
q 2 a2
4 2
4 2
q
E
q
E0
dI
2
2
t
0

sin
θ

sin
θ

I

.
3
2 3
2 3
d
4 c
8 m c
3m c
θ – угол между a (т.е. E0) и направлением испускания излучения n.
Сечение рассеяния электромагнитной волны зарядом:
2
dσ dI d   q 2 
I
8  q 2 
2

  2  sin θ; σ 

 2
d
S t
mc
S
3


 mc 
t
2

cE2 
S 
.
4 

S – плотность потока (длина вектора Пойнтинга) начальной волны.
Если начальная волна не поляризована, то необходимо усреднить
полученные результаты по всем возможным направлениям вектора E0:
1  cos 
sin θ 
2
2
2
2
 q  1  cos 2 
 dσ 
 
 2 
.

2
 d  unpolarized  mc 
2
φ – угол между направлениями (волновыми векторами) начальной и
рассеянной волн.
Если заряженной частицей является электрон, то мы получаем знаменитую
формулу для сечения томсоновского рассеяния:
8
σT 
3
2
 e  8 2
re  0, 665 барн
 2 
3
 mc 
2


e2
13
r


2,82

10
см
 e
.
2
me c


Рэлеевское рассеяние
В 1871 г. английский физик лорд Рэлей вывел формулу для сечения рассеяния
света с частотой  на осцилляторе с массой m, зарядом q и частотой 0 (>> ) :
8
σR 
3
 q 
 2
 mc 
2
 
 σT  
 0 
2
 
 
 0 
4
4
Угловое распределение рассеянного
света такое же как и в случае
Джон Уильям Стретт, лорд Рэлей
(John William Strutt, 3rd Baron Rayleigh,
1842 – 1919)
томсоновского рассеяния
неполяризованного света.
Рэлеевское рассеяние объясняет голубой цвет неба днем («синяя» часть
спектра рассеивается наиболее сильно) и красный цвет солнца на закате
(«красная» часть спектра рассеивается наиболее слабо).
Рэлеевское рассеяние
на атоме
В борновском приближении
kf
сечение рэлеевского рассеяния
θ
есть
dσ R dσ T
2

F (q) ,
d d
k0
F (q)   exp  iq  r  ρ  r  dr
q  k 0  k f .
F(q) – атомный форм-фактор [F(0)=Z]; ρ(r) – электронная плотность.
В силу сферической симметрии атома ρ(r)=ρ(r), имеем:

4
4
θ

F (q) 
sin
qr
ρ
r
rdr
q

2
k
sin
θ

sin
   
0

.

q 0

2

F(q)
(1/λ)sin(θ/2) [Å-1]
(1/λ)sin(θ/2) [Å-1]
Рис. Характерные значения сечения рэлеевского рассеяния на атоме
составляют 100-1000 барн.
Раздел III.
3. Упругое рассеяние -квантов на кристаллах.
Кристалл представляет собой упорядоченную
структуру из атомов (решетку). В отличие от света,
длины волн рентгеновского и -излучения не
превышают межатомных расстояний, а
следовательно возможно явление дифракции на
такой структуре. Дифракция может быть
использована как для анализа кристаллической
структуры (т.н. рентгеноструктурный анализ), так и
для спектрометрии -излучения (например, с
помощью спектрометра Брэгга).
История открытия
Макс фон Лауэ
(Max von Laue, 1879 – 1960)
В 1911 г. профессор Мюнхенского университета
Арнольд Зоммерфельд поручил приват-доценту
Максу Лауэ написать статью о волновой оптике
для математической энциклопедии. Лауэ
подошел к заданию очень серьезно и
педантично. Как-то в январе 1912 г. он
прогуливался с Паулем Эвальдом (аспирантом
Зоммерфельда) по Английскому саду в
Мюнхене. Эвальд рассказывал о теме своей
диссертации – поведение световых волн в
кристалле. У Лауэ возник вопрос: как будут
вести себя очень короткие электромагнитные
волны (λ << d) в кристалле? Если рентгеновское
излучение представляет собой
электромагнитные волны, то при прохождении
его через кристалл должна наблюдаться
дифракция!!!
Схема опыта Лауэ, Фридриха и
Книппинга
Лауэ предложил эксперимент,
который позволил бы проверить
выдвинутую им гипотезу. В апреле
1912 г. Вальтеру Фридриху
(ассистенту Зоммерфельда) и
аспиранту Мюнхенского университета
Паулю Книппингу удалось направить
на кристалл медного купороса
(сульфата меди) узкий пучок
рентгеновского излучения и
зафиксировать рассеянное на
кристалле излучение на
фотопластинке. Их первым успехом
была дифракционная картина из
темных точек, которую они увидели,
когда проявили пластинку (темные
пятна на негативе соответствуют
большой засветке). Ныне такие
дифракционные картины носят
название лауэграмм.
Лауэграмма поваренной соли
(NaCl)
Лауэграмма кристалла каменной соли (NaCl), полученная с помощью 60 кВ
рентгеновской трубки с вольфрамовым анодом. Во избежание передержки
пленки в центре был помещен свинцовый диск, который убрали только в
последнюю секунду 40-минутной экспозиции.
Лауэграмма цинковой обманки
(ZnS)
Нобелевская премия по физике
(1914 г.)
«За открытие дифракции X-лучей
кристаллами»
Макс фон Лауэ
(Max von Laue, 1879 – 1960)
История (продолжение)
Вильямы Брэгги (сын и отец)
Брэгг-старший считал рентгеновское
излучение потоком частиц. Однако
опыт Лауэ изменил его мнение.
Обсуждения статьи Лауэ отцом и
сыном Брэггами в 1912 г. привели их к
созданию рентгеноструктурного
анализа – метода исследования
кристаллов, основанного на
дифракции рентгеновского
излучения.
В качестве первых объектов исследования были
выбраны NaCI, KCI, KBr, алмаз, ZnS.
Знаменитый фундаментальный результат
Брэггов: поваренная соль (NaCI) – это кристалл
из ионов Na+ и Cl-, а не молекул NaCI (открытие
ионных кристаллов!!!).
Закон Брэгга (младшего)
Брэгг-младший пришел к убеждению, что Лауэ усложнил описание деталей
дифракции. Атомы в кристаллах располагаются в плоскостях, и Брэггмладший предположил, что дифракционная картина конкретного вида
вызывается расположением атомных плоскостей в конкретной
разновидности кристаллов. Если это так, то рентгеновскую дифракцию
можно было использовать для определения структуры кристаллов.
В 1913 г. он опубликовал
уравнение, позже названное
законом Брэгга, описывающее
углы, под которыми следует
направить пучок рентгеновских
лучей, чтобы определить
строение кристалла по
дифракционной картине
рентгеновских лучей, отраженных
от кристаллических плоскостей.
Спектрометр Брэгга (старшего)
В том же 1913 г. Брэгг-старший изобрел
спектрометр рентгеновского излучения,
принцип работы которого был основан
на законе Брэгга-младшего.
Схема работы спектрометра.
Коллимированный пучок ХРИ от
рентгеновской трубки, выделенного с
помощью подходящих фильтров,
падает на грань скола кристалла.
Кристалл совершает покачивания
вокруг оси О. Максимум отражения для
разных длин волн наблюдается под
разными углами.
Нобелевская премия по физике
(1915 г.)
«За вклад в анализ кристаллов с
помощью X-лучей»
Брэгг-младший
стал самым
молодым
лауреатом за
всю историю
Нобелевских
премий!
Сэр Вильям Генри Брэгг
(Sir William Henry Bragg, 1862 – 1942)
Вильям Лоренс Генри Брэгг
(William Lawrence Bragg, 1890 – 1971)
«Элементарная» теория
Аналогично рэлеевскому рассеянию, с учетом трансляционной симметрии
кристалла, имеем для дифракционного рассеяния (рассеяния Лауэ):
2
dσ L dσ T

Fcrystal (q)
d d
Fcrystal (q) 

e
q  k i  k f  ,
iq n1a1  n2a 2  n3a3 
Fatom (q)
n1 , n2 , n3
 NFatom (q)  q ,G
G

dσ L dσ T
2

Fatom (q)   q ,G .
d d
G
G=hb1+kb2+lb3 – вектор обратной решетки кристалла exp[iG(n1a1+n2a2+n3a3)]=1:
G задает набор атомных плоскостей (dhkl=2π/G, G  плоскостям)!
Объяснение закона Брэгга
dσ L dσ T
2

Fatom (q)   q ,G .
d d
G
4
2 n
q  2ki sin θ 
sin θ, G 

d
q  G  2d sin θ  n.
 n  0,1, 2, 
Сфера
Эвальда
Раздел III.
4. Неупругое рассеяние (Комптон-эффект).
Если для длинноволновых фотонов
преобладает упругое (когерентное)
рассеяние на атомах, то для
коротковолновых – неупругое
(некогерентное). Неупругое рассеяние кванта на электроне атома
сопровождается увеличением длины
волны -кванта (эффект Комптона или
Комптон-эффект). При этом -квант
выбивает из атома электрон («электрон
отдачи»).
История открытия
В 1919 г. американский физик Комптон, работая в
Кавендишской лаборатории (как стипендиат одного
года) с радиоактивными источниками -квантов,
заметил, что рассеянное излучение легче
поглощается веществом, чем первичное.
Артур Комптон
(Arthur Holly Compton,
1892 – 1962)
Вернувшись в США в 1920 г., Комптон с помощью
спектрометра Брэгга провел точные измерения
длин волн рассеянных рентгеновских лучей. Он
обнаружил в рассеянном излучении две
компоненты: (1) с начальной длиной волны и (2) с
бóльшей длиной волны (Δλ ~ θ, θ – угол рассеяния).
Увеличение длины волны получило название
эффекта Комптона.
Эксперимент
Комптона
Источником рентгеновского
излучения служила катодная
трубка с молибденовым анодом.
С помощью фильтров
выделялась Kα-линия в ХРИ
молибдена. Рассеивателем был
графит. Рассеянное излучение
анализировалось в спектрометре
Брэгга, в котором использовался
кристалл кальцита (CaCO3,
d=310-8 см) и ионизационная
камера (максимум тока отвечает
выполнению условия Брэгга). В
спектре наблюдалась исходная
Kα-линия и смещенная линия с
большей длиной волны.
В 1923 г. Комптон опубликовал свои
результаты и предложил их «квантовую»
интерпретацию. Также он выдвинул
предположение об «электронах отдачи»,
которые должны вылетать из атомов с
большой скоростью в результате
рассеяния на них -квантов. В том же
1923 г. шотландский физик Вильсон с
Чарльз Вильсон
(Charles Thomson Rees Wilson,
1869 – 1959)
помощью своей конденсационной камеры
(изобретена им в 1910-1912 гг.)
обнаружил «электроны отдачи».
½ Нобелевской премии по физике
(1927 г.)
«За открытие эффекта, названного в
его честь»
Артур Комптон
(Arthur Holly Compton,
1892 – 1962)
½ Нобелевской премии по физике
(1927 г.)
«За создание метода визуализации
траекторий заряженных частиц с
помощью конденсации пара»
Чарльз Вильсон
(Charles Thomson Rees Wilson,
1869 – 1959)
Объяснение эффекта
Комптона
Рассмотрим рассеяние фотона на покоящемся электроне (Ei >> I):
2

Ei  E f 

2
 Ei  me c 2  E f  Ee ,
 pe 
 2me  Ei  E f  ,
2
 

c
pi  p f  p e ;
 2
2
2
p

p

p
i
f  2 pi p f cos θ;
 e
 1
1  1  cos θ
 
 

p

me c
 f pi 
h
  f  i   m c 1  cos θ  .
e
Формула Комптона (λe – комптоновская длина волны электрона):

f
 i   e 1  cos θ 

e
 h me c  2, 426 1010 см 
Эффект Комптона в КЭД
Диаграммы Фейнмана низшего порядка для рассеяния фотона электроном
Формула Кляйна-Нишины (1929 г.; e- покоится,  и e- не поляризованы):
2



dσ 1 2  E f   E f Ei
e
2
 re 

 sin θ   re 
 2,81 Фм  ,
 
2

d  2  Ei   Ei E f
me c

 
Ei
Ei
Ei
dσ  dσ T 
 1:
 1
1  cos θ  

.

2 
2
Ef
me c
me c
d   d  unpolarized
2
Угловое распределение
фотонов
Спектр рассеянных фотонов
Ei
 E f  Ei
2 Ei
1
me c 2
Полное сечение

Ei
2 Ei 
1: σ  σ T 1 
.
2
2 
me c
 me c 
Ei
3me c 2  2 Ei 1 
 .
1: σ  σ T
 ln
2
2
me c
8 Ei  me c
2
σT 
8 2
re  0, 665 барн
3
Электроны отдачи
Из законов сохранения энергии и
импульса находим для угла вылета
электрона находим:
Ei 
θ
tg ψ  ctg 1 

2  me c 2 
1
Т.е. электроны отдачи вылетают только
в переднюю полусферу (ψ < π/2)!
Электроны отдачи (спектр)
2 Ei2
0  Te 
me c 2  2 Ei
Основные свойства Комптонэффекта (КЭ)
•Сечение КЭ ~ Z (некогерентная сумма вкладов
отдельных электронов);
•Сечение КЭ падает с ростом E:
≈ σT, если E << mec2;
~ ln(E)/E, если E >> mec2;
•Ядерный вклад в сечение КЭ очень мал, т.к.
классический электромагнитный радиус ядра
rя = Z2e2/(Mяc2) ~ 10-3-10-4re.
Раздел III.
5. Обратный эффект Комптона.
Комптоновское рассеяние на движущемся
электроне может приводить к уменьшению длины
волны -кванта (обратный эффект Комптона). Это
явление можно использовать для преобразования
светового излучения в достаточно
монохроматическое и поляризованное -излучение.
Кроме того, это явление возможно объясняет
наличие изотропного рентгеновского и -фона во
Вселенной (обратное комптоновское рассеяние
реликтовых фотонов (T=2,7 K) на
ультрарелятивистских электронах в космосе).
Механизм
обратного КЭ
Пусть энергия фотона много меньше энергии электрона (E0 << E0).
Используем уже полученные результаты, переходя из системы покоя
электрона в лабораторную систему, где электрон движется со скоростью v:
В случае лобового столкновения (θ = π) с рассеянием назад (φ = π) и v ≈ c:
Для рубинового лазера (E0=1,78 эВ)
Е0
max
1 ГэВ
6 ГэВ
40 ГэВ 500 ГэВ
28
МэВ
848
МэВ
20 ГэВ 497 ГэВ
Применение
Для получения комптоновских пучков целесообразно использовать электронные
накопители. Схема установки РОКК-2 в Новосибирске (РОКК – Рассеянные
Обратные Комптоновские Кванты).
Параметры установок с пучками
обратных комптоновских фотонов
Установка
Накопитель
Ladone
Taladone
Adone
(Фаскати)
LEGS
GRAAL
NSLS
ESRF
(Брукхэвен) (Гренобль)
LEPS
SPring-8
(Осака)
Энергия электронов,
ГэВ
1.5
1.5
2.5
6.04
8.0
Ток электронов, А
0.1
0.1
0.2
0.1
0.2
Энергия лазерных
фотонов, эВ
2.45
2.45
3.53
3.53
3.5
Энергия комптоновских
квантов, МэВ
5-80
35-80
180-320
550-1470
150-2400
Разрешение по энергии
(FWHM), МэВ
0.07-8
4-2
6
16
30
105
5.105
4.105
2.106
107
Интенсивность гаммаквантов, с-1
Раздел III.
6. Рождение пар.
При энергиях -кванта, превышающих
значение 2mec2 = 1,022 МэВ, становится
энергетически возможным процесс
рождения -квантом пары электронпозитрон в поле ядра. Вся энергия -кванта
передается образованной паре и ядру
отдачи, т.е. он аннигилирует. Рождение пар
является доминирующим процессом
взаимодействия с веществом -квантов с
энергией ~ 100 МэВ и выше.
Историческая справка
Поль Дирак
(Paul Adrien Maurice Dirac,
1902 — 1984)
В 1928 г. английский физик Поль Дирак вывел свое
знаменитое уравнение, которое в отличие от
уравнения Шредингера описывало релятивистский
электрон. Среди решений уравнения были также на
первый взгляд нефизические – состояния с
отрицательной энергией. Дирак не стал их
отбрасывать – он предположил, что все электроны
Вселенной занимают уровни с отрицательной
энергией, образуя ненаблюдаемый фон.
Наблюдаемы только электроны с положительной
энергией. "Незаполненные состояния с
отрицательной энергией представляются как нечто с
положительной энергией, потому что для того, чтобы
они исчезли, необходимо внести туда один электрон
с отрицательной энергией. Мы предполагаем, что эти
незанятые состояния с отрицательной энергией суть
протоны".
Дирак теоретически предсказал возможность
рождения электрон-антиэлектронной пары из фотона
достаточно большой энергии.
Поль Дирак любил потеоретизировать на самые
различные темы. Однажды он высказал
предположение, что существует оптимальное
расстояние, на котором женское лицо выглядит
привлекательнее всего; поскольку в двух
предельных случаях – на нулевом и бесконечном
расстоянии – «привлекательность обращается в
нуль» (ничего не видно), то между этими
пределами, естественно, должен существовать
максимум. 
Дирак любил выражаться точно и требовал точности от других. Однажды на
семинаре в конце длинного вывода докладчик обнаружил, что знак в
окончательном выражении у него не тот. «Я в каком-то месте перепутал
знак», – сказал он, всматриваясь в написанное. «Вы хотите сказать – в
нечетном числе мест», – поправил с места Дирак. 
В другой раз Дирак сам был докладчиком. Окончив сообщение, он обратился
к аудитории: «Вопросы есть?». – «Я не понимаю, как вы получили это
выражение», – спросил один из присутствующих. «Это утверждение, а не
вопрос, – ответил Дирак. – Вопросы есть?» 
Нобелевская премия по
физике (1933 г.)
«За открытие новых
продуктивных форм атомной
теории»
Эрвин Шредингер
(Erwin Schrödinger,
1887 — 1962)
Поль Дирак
(Paul Adrien Maurice Dirac,
1902 — 1984)
Историческая справка
Карл Давид Андерсон
(Carl David Anderson,
1905—1991)
В начале 1930 гг. американский физик Карл
Андерсон начал исследования космических лучей
(под руководством Роберта Милликена). Во время
исследований он открыл необычные треки
некоторой частицы на снимках пузырьковой камеры,
которые он правильно интерпретировал как треки,
принадлежащие частице с массой электрона, но
имеющей противоположный электрический заряд.
Это открытие, объявленное в 1932 г., и впоследствии
подтверждённое другими, подтвердило
теоретические рассуждения Поля Дирака о
существовании антиэлектрона – позитрона.
Андерсон получил первое прямое доказательство
существования позитрона путём облучения гаммалучами, произведёнными карбидом тория (ThC),
других материалов, что привело к образованию
электрон-позитронных пар.
½ Нобелевской премии по
физике (1936 г.)
«За открытие позитрона»
Карл Давид Андерсон
(Carl David Anderson,
1905—1991)
Порог рождения
В вакууме процесс  → e- + e+ невозможен!
Действительно, предположим обратное. Тогда в
СЦИ электрона и позитрона имеем:
2

E

2
m
c
 E  p c  ,   p  2mec,
 
e




 p  0;
p  pe  pe  0;
Таким образом, для рождения пары необходимо присутствие 3-го тела!
Рассчитаем порог рождения пары Eпор в поле тела массой M, используя
релятивистский инвариант (ΣEi)2-(Σpi)2c2 = (ΣEf)2-(Σpf)2c2 = inv:
E
пор

 Mc
   E    2m c
2 2
ЛС
пор 2

e
2
 Mc

2 2
 E
пор
 me 
 2me c 1 
.
 M
2
СЦИ
В поле ядра Eпор  2mec2 (т.к. Mя >> me), а в поле электрона Eпор = 4mec2.
Рождение пары с
точки зрения КЭД

x
Диаграммы Фейнмана
низшего порядка для

процесса рождения
x
электрон-позитронной
виртуальный
фотон
пары в поле заряженной
Z 
частицы (наверху) и ядра
(справа). Поворот линии
Ядро, Ze
-кванта и позитрона на
180 дает диаграмму для
тормозного излучения
электрона в поле ядра!
x
Вероятность процесса:
2
A ~
2
    Z   Z 2 3
Экранировка
Когда b ≥ a, где a = a0Z-1/3 – радиус
атома в модели Томаса-Ферми,
становятся важными эффекты
экранирования заряда ядра
электронами атома. Для оценок
воспользуемся соотношением
неопределенности для виртуального
bmax 
c
h v,min
h v,min  h 
bmax
,
h v,min
c
E

 2
h

 p  p
c
 me2c 4 
h  c
h
 2 4 
 a0
2
me c
me c

E

 2
фотона bhv/c ≥ ћ.
Из правила треугольника!
2 4
m
2 4
ec
 me c 
h
2
E

m
c


e
Если E = h >> 137mec2Z-1/3, то
сильная экранировка!
Сечение рождения пары
В нерелятивистской области (0 < E - 2mec2 << mec2), где тем не менее
скорости электрона и позитрона достаточно велики, чтобы использовать
борновское приближение по взаимодействию с ядром, электроны и позитроны
летят преимущественно перпендикулярно направлению -кванта. Полное
сечение:
E

2
2
σ  Z  re 
 2
2
12
 me c


3


e2
 2,82 Фм  .
 re 
2
me c


В ультрарелятивистской области (E >> mec2) электроны и позитроны
летят в направлении -кванта под углом ~ mec2/E. Полное сечение:
 28 2 E 218 
σ  Z  r  ln


2
9
m
c
27
e


2
2
e
 28 183 2 
σ  Z  r  ln 1 3  
27 
 9 Z
2
2
e
m c
e
2
 E  137me c 2 Z 1 3  ,
2 1 3
E

137
m
c
Z .
 
e
Вероятность рождения пары в
веществе
Учет образования пар на электронах атома приводит к результату:
 28 183 2 
σ  Z  Z  1  r  ln 1 3  
27 
 9 Z
2
e
2 1 3
E

137
m
c
Z .
 
e
Вероятность рождения пары в слое вещества с плотностью n и толщиной l:
dP  x   1  P  x  σ  E  ndx  P  l   1  exp  σ  E  nl  .
В случае, когда E>>137mec2Z-1/3:
 7 l 
P  l   1  exp  

 9 l рад 
 1
183 
2
 4Z  Z  1  re ln 1 3  .


l
Z
рад


Здесь lрад – радиационная длина (см. тормозное излучение).
Значения радиационных длин
для некоторых веществ
P
Вероятность рождения пары в единичном
акте взаимодействия -кванта
Электрон-фотонный ливень
Образование электрон-позитронных пар
приводит к возникновению электроннофотонных ливней в космических лучах.
Если энергия -кванта достаточна, то он
может родить пару. Электрон и позитрон
могут испустить тормозные -кванты, которые
в свою очередь могут родить электронпозитронные пары. В результате возникает
лавинообразный процесс, который однако
быстро затухает, когда кинетические энергии
рождающихся электронов и позитронов
становятся меньше критической энергии
Ткр≈700/Z МэВ (ниже которой ионизационные
потери доминируют над радиационными).
Рождение пар мюонов и пионов
(1) Если E > 2mμc2 ≈ 211 МэВ, то возможно рождение -квантом в кулоновском
поле ядра лептонной пары μ. Сечение такого процесса много меньше сечения
фоторождения пары e. Действительно
σ  γ  e  e 
σγ  μ  μ



~
2
e
2
m2
r
 2  4 104.
r me
(2) Если E > mπc2 ≈ 140 МэВ, то возможна
фотогенерация пиона. По сути это
фоторождение легкой пары кварк-антикварк в
электромагнитном или сильном поле ядра.
Сечение этого процесса ~ A10-28 см2, т.е. тоже
много меньше, чем сечение фоторождения e.
Сечение фоторождения
адронов на нуклонах ядра
Основные закономерности
процесса рождения пар
• Процесс имеет энергетический порог:
2mec2 = 1,022 МэВ;
• Сечение ~ Z2;
• С ростом энергии сечение сначала растет, а при
энергиях ~ 100 МэВ «выходит на константу»
~ Z210-26 см2;
• При энергиях ~ 150 МэВ появляется
возможность фоторождения пионов, ядерных
Δ-резонансов и т.д. Cечения таких процессов
~ A10-28 см2.
Раздел II.
9. Аннигиляция позитронов.
Аннигиляция позитрона и электрона – это
процесс, обратный рождению пары
электрон-позитрон. Однако, в отличие от
рождения пары аннигиляция не требует
обязательного присутствия 3-го тела. При
этом возникает как минимум два
аннигиляционных -кванта. Если в вакууме
позитрон живет бесконечно долго, то,
например, в типичных твердых средах он
аннигилирует в среднем за 10-10 с. Наряду
с рождением пар, естественным
источником позитронов служит β+-распад.
Историческая справка
Возможность аннигиляции пар была теоретически предсказана в 1930 г.
английским физиком Полем Дираком. В 1932 г. американский физик Карл
Андерсон открыл позитрон в космических лучах с помощью пузырьковой
камеры. В 1933 г. Ирен и Фредерик Жолио-Кюри с помощью камеры Вильсона,
помещенной в магнитное поле, наблюдали рождение электрон-позитронных
пар гамма-квантами от радиоактивного источника. В том же году Ф. ЖолиоКюри и независимо Ж. Тибо надёжно зарегистрировали случаи аннигиляции
пар электрон-позитрон.
Поль Дирак
Карл Андерсон
Ирен и Фредерик
Жолио-Кюри
Специфика процесса
В вакууме процесс  → e- + e+ невозможен 
обратный процесс e- + e+ →  тоже невозможен!
Однако присутствие 3-го тела для аннигиляции вовсе необязательно, т.к.
законы сохранения энергии-импульса можно удовлетворить, если e- + e+ → n,
где n ≥ 2!!!
Наиболее важным является случай 2-х фотонной аннигиляции (n = 2), который
как правило «венчает» конец тормозного пути позитрона в веществе: позитрон
тормозится за счет ионизационных и радиационных потерь (аналогично
электрону) и, достаточно замедлившись, аннигилирует с электроном вещества.
При этом с высокой вероятностью образуются два -кванта, каждый с энергией
E  mec2 = 511 кэВ, которые летят в противоположных направлениях.
Аннигиляция с точки зрения
КЭД
Диаграмма Фейнмана для
2-х фотонной аннигиляции:
Вероятность процесса:
σ 2γ ~ M


σ 2γ ~
M =

2
2
   2

σ nγ ~  n
Сечение
2-х фотонной
аннигиляции
В системе покоя электрона в нерелятивистском случае:
σ 2γ   re2
с



e2
 2,82 Фм  .
 re 
2
me c


Вероятность аннигиляции в единицу времени в веществе с зарядом Z и
атомной плотностью n:
w  Znσ2γ  dx dt   Znσ2γ  Zn re2c.
Время жизни медленного позитрона в веществе  =1/w (для свинца  ≈10-10 с).
В ультрарелятивистском случае
(в системе покоя электрона):
me  2 E 
σ 2γ   r
 1 .
 ln
E  me

2
e
Позитроний (Ps)
При движении в веществе позитрон замедляется, теряя энергию на ионизацию
и излучение (аналогично электрону). В конце тормозного пути позитрон вместе
с «возмущенным» электроном вещества могут образовать связанное
состояние – позитроний (positronium – Ps). С вероятностью 25% образуется
парапозитроний (p-Ps: S=0, MS=0) и 75% – ортопозитроний (o-Ps: S=1,
Ms=−1,0,1). Спектр связанных состояний Ps аналогичен водороду:
e4 
 2 с2
6,8 эВ
 n  Ps    2 2  


2n
2n 2
n2

me me
me 

  
 .
me  me
2 

Измерения энергий переходов между состояниями Ps можно использовать для
проверки КЭД и точных измерений постоянной тонкой структуры α (поскольку в
случае водорода присутствует неопределенность, связанная с внутренней
структурой протона).
Распад позитрония
Парапозитроний (1S0) распадается на 2n (сохранение
зарядовой четности, отбор по спину!). Скорость распада
e
Ps
w0 получается из сечения аннигиляции свободной
неполяризованной электрон-позитронной пары 2:
w0  4   0   σ 2γ 
2
e+

 0
me c 2 5

.
2
Отсюда, время жизни 0=1/w0=1,2310-10 с.
Ортопозитроний (3S1) распадается на 3n. Аналогично:
e-

Ps

e+

4
w1    0   σ3γ 



0

3
r


1
e a,
  r  
3

a

2
2  2  9  me c 2 6
9
2 2 
a
.
2 
me e 
Отсюда, время жизни 1=1/w1=1,410-7 с.
Распад позитрония в веществе
«Счастливый» Ps (слева) живет
больше, чем «несчастный» Ps
(справа), т.к. реже
Зависимость времени жизни от радиуса
полости.
«встречается» с электронами
вещества.
Однофотонная аннигиляция
При столкновении позитрона со связанным электроном возможна их
аннигиляция в один фотон. Амплитуда процесса однофотонной аннигиляции
на электроне атома e++A→A++ аналогична амплитуде фотоэффекта
+A→A++e- (ср. рождение пары и тормозное излучение)! Сечение
однофотонной аннигиляции на K-электроне в нерелятивистском случае
(+<<c):
 1 
4 2 5 4 
re Z 
.
3
c
В ультрарелятивистском случае (E+>>me):
me
 1  4 r Z 
.
E
2
e
5
4
Ремарка. Для свинца максимальное значение 1/2≈0,2 при E+/me~10.
Основные закономерности
аннигиляции позитрона
• Наиболее вероятна двухфотонная
аннигиляция;
• Сечение аннигиляции:
~ 1/+ при + << c,
~ 1/E+ при E+ >> me;
• Вероятность аннигиляции ~ Z;
• Время «жизни» медленного позитрона в
твердом веществе ~ 10-10 с.
Раздел III.
7. Поглощение -квантов в веществе.
Ослабление потока -квантов в веществе
происходит в результате трех неупругих
процессов: фотоэффект, Комптон-эффект,
образование пары в поле атомного ядра.
Таким образом, чем больше заряд и
плотность среды, тем эффективнее она
поглощает -кванты. Поглощающую
способность вещества принято
характеризовать линейным и массовым
коэффициентами поглощения. Эти
коэффициенты определяют кривую
поглощения данного вещества.
Кривая поглощения
Пусть на тонкий слой вещества нормально поверхности падает поток -квантов
I0. В приближении однократного взаимодействия на глубине x имеем:
dI  x   I  x  nσtot dx  I  x   I 0 exp  nσtot x  .
n – атомная плотность; tot – полное сечение неупругого взаимодействия:
σ tot  σФЭ  σКЭ  σРП .
Линейный коэффициент поглощения  [см-1]:
I  x   I 0 exp   x  ,
  nσtot .
Массовый коэффициент поглощения μ [см2/г]:
I  x   I 0 exp   ρx  ,
ρ – плотность вещества.

nσ tot
 
.
ρ
ρ
Полное сечение взаимодействия σtot в углероде (слева) и свинце (справа)
как функция энергии фотона. σp.e. – атомный фотоэффект; σcoherent – упругое
(рэлеевское) рассеяние; σincoh – эффект Комптона; N(e) – образование пар в
поле ядра (электронов); σnuc – фотоядерное поглощение (ГДР).
Линейный коэффициент
поглощения
Раздел III.
Заключение.