Анализ статистических характеристик
реклама

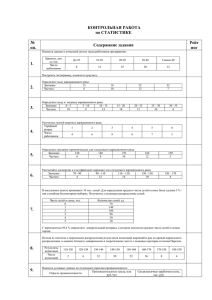
globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. Конарева А.Ю. ФФ 4-10 Цель - закрепление теоретического и практического материала, приобретение навыков работы с вариационными рядами в Microsoft Office Excel 2007. Задание - необходимо провести анализ статистических характеристик дискретного и интервального ряда в Microsoft Office Excel. Ход работы: 1. Формирование таблицы исходных данных в среде в Microsoft Office Excel Исходные данные представлены в табл.1. Таблица 1 Уставный капитал банков X ПриватБанк 4214,3 Аваль 2515,1 Укрсоцбанк 1599,2 Укрисиббанк 1559,4 Ощадбанк 863,5 Правекс-банк 846,8 Надра 772,6 Брокбизнесбанк 669,7 Райффайзенбанк 611 Финансы и кредит 374,5 Прокредитбанк 350,8 Проминвестбанк 333,4 Кредитпромбанк 216,5 ТАС-комерцбанк 158,6 Експрес-банк 155,4 Индустриальноэкспортный 150,1 Форум 146,2 Укргазбанк 134,5 Киев 129 Укрпромбанк 128,5 Кредитбанк 128,3 ТаАС-инвестбанк 100,4 Родовидбанк 97,1 Вабанк 89,2 globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. 2. Рассчет статистических характеристик ряда (среднее, дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициенты асимметрии и эксцесса). Для расчета основных статистических характеристик дискретного вариационного ряда, воспользуемся Мастером функций. Результат расчета статистических характеристик для дискретного ряда приведен на рис.1. Рис.1. Статистические характеристики дискретного ряда 3. Превращение дискретного вариационного ряда в интервальный ряд Для построения интервального вариационного ряда необходимо рассчитать шаг группировки (рис.2). globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. Рис.2. Расчет шага группировки Сформированные интервалы вариационного рассчитанными частотами приведены на рис.3. ряда с Рис.3. Сформированные интервалы вариационного ряда 4. Расчет основных статистических характеристик вариационного ряда (среднее, дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициенты асимметрии и эксцесса) Таблица промежуточных результатов расчета статистических характеристик изображена на рис. 4. указанных globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. Рис. 4. Промежуточные результаты расчета статистических характеристик интервального вариационного ряда Результаты расчетов статистических характеристик дискретного и интервального рядов изображены на рис. 5. Рис. 5. Результаты расчета основных характеристик дискретного и интервального рядов для статистических globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. 5. Графическое изображение дискретного и интервального вариационных рядов График изображения дискретного вариационного ряда, у которого по оси X - номер объекта, а по оси Y - значение исследованного показателя представлено на рис. 6. X 4500 4000 3500 3000 2500 2000 1500 1000 500 0 Вабанк Родовидбанк ТаАС-инвестбанк Кредитбанк Укрпромбанк Киев Форум Укргазбанк Индустриальноэксп… Експрес-банк ТАС-комерцбанк Проминвестбанк Кредитпромбанк Прокредитбанк Финансы и кредит Райффайзенбанк Надра Брокбизнесбанк Правекс-банк Ощадбанк Укрисиббанк Аваль Укрсоцбанк ПриватБанк X Рис.5. График изображения дискретного вариационного ряда в Microsoft Office Excel Гистограмма распределения частота изображена на рис.7. эмперич.частоты 25 20 15 10 эмперич.частоты 5 0 604.8375 1636.1125 2667.3875 3698.6625 globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. Рис.7. Гистограмма распределения частот интервального ряда в Microsoft Office Excel График куммуляты частота изображен на рис.8. накопл.частоты 25 24 23 22 накопл.частоты 21 20 19 18 1 2 3 4 Рис.8. График куммуляты частот в Microsoft Office Excel 6. Проверка гипотезы о нормальном законе распределения ряда с помощью критерия Пирсона и Колмагорова-Смирнова. На рис. 9 изображена таблица, теоретические частоты исследуемого ряда. Рис.9. Расчет распределения теоретических в частот которой рассчитаны нормального закона На рис. 10 изображен порядок расчета указанных выше критериев. лямда p(лямда) 39,5 0 globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. X^2 91,573 P(X^2)(k=4-1) 0 Рис.10. Расчет критериев Пирсона и Колмогорова-Смирнова Из расчетов, приведенных в рис.10, видно, что гипотеза про нормальность исследуемого ряда не подтверждается. Полученное значение Х^2p равно 91,573, что больше табличного значения при заданном уровне вероятности. Вероятность, соответствующая данному значению критерия равная единице и подтверждает практически полное отсутствие различий между эмпирическими и теоретическими значениями. Визуально это можно увидеть на рис. 11. 35 30 25 20 20 2 1 1 15 тер.частоты f* 10 5 0 1 2 3 4 Выводы В результате расчета статистических характеристик дискретного ряда было определено, что среднее значение уставного капитала для банков Украины составляет 681 тыс. грн. Половина банков имеет размер капитала ниже 274,95 тыс. грн., а вторая половина – выше данного значения. Разница между наибольшим и наименьшим размером уставного капитала составляет 4125,1 млн. грн. Дисперсия для данного ряда составляет 931998, а среднее квадратическое отклонение - 965 тыс. грн. Т.к. коэффициент асимметрии рамен 2,61. Коэффициент эксцесса больше 0 и равен 7,58, что свидетельствует о том, что распределение относится к островершинным. globalteka.ru - Грамотное и качественное выполнение всех видов научных работ. Скидки, оригинальность, контроль плагиата, прямое общение с автором. В результате преобразования дискретного ряда в интервальный был получен ряд распределений, состоящий из 4-х интервалов. Расчет статистических показателей для интервального ряда дает возможность сделать следующие выводы. Средний размер уставного капитала для банков Украины составляет 905 тыс. грн. Наиболее часто встречающийся размер уставного капитала – 631,9 тыс. грн. Половина банком имеют уставный капитал в размере более 707,9 тыс. грн.. а вторая часть – менее данного значения. Дисперсия в интервальном ряду равна 574231, при этом значение стандартного отклонения составляет 757 тыс. грн., что свидетельствует степени отклонения размеров уставных капиталов банков от среднего значения в обе стороны. Коэффициент эксцесса больше 0 и равен 8,9, что свидетельствует о том, что распределение относится к островершинным. Для оценки близости теоретического и эмпирического распределений были использованы особые показатели – критерии согласия Пирсона и Колмогорова-Смирнова. «Хи-квадрат» - критерий Пирсона является случайной величиной, имеющей распределение, близкое к распределению «хи-квадрат». В данном случае Х^2р≤ X^2к при заданном уровне значимости равном 91,5, что свидетельствует о том, что распределения являются не близкими друг другу и различия между ними существенны. Полученному значению «лямбда»- критерия» Колмогорова-Смирнова, равному 39,5, соответствует вероятность близкая к 0. Полученное значение вероятности свидетельствует о том, что расхождение между эмпирическим и теоретическим распределениями существенны, вызваны случайной вариацией признака в статистической совокупности. В основе эмпирического распределения банков по размеру их уставного капитала лежит закон нормального распределения.