3 - Reshaem.Net

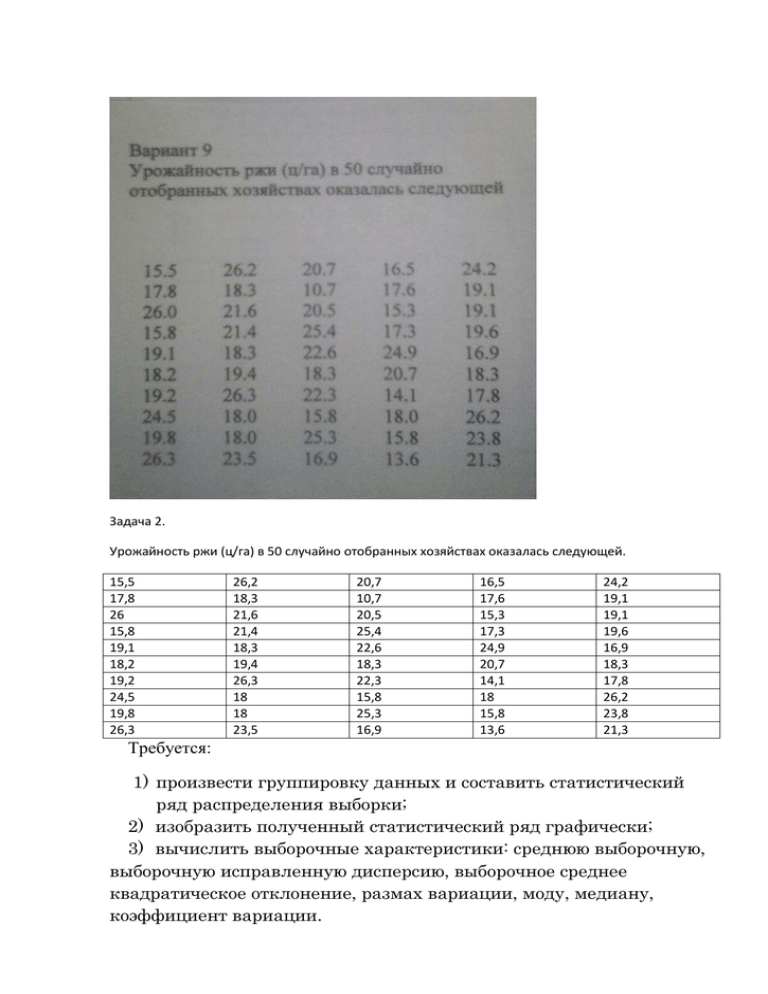
Задача 2.
Урожайность ржи (ц/га) в 50 случайно отобранных хозяйствах оказалась следующей.
15,5
17,8
26
15,8
19,1
18,2
19,2
24,5
19,8
26,3
26,2
18,3
21,6
21,4
18,3
19,4
26,3
18
18
23,5
20,7
10,7
20,5
25,4
22,6
18,3
22,3
15,8
25,3
16,9
16,5
17,6
15,3
17,3
24,9
20,7
14,1
18
15,8
13,6
24,2
19,1
19,1
19,6
16,9
18,3
17,8
26,2
23,8
21,3
Требуется:
1) произвести группировку данных и составить статистический
ряд распределения выборки;
2) изобразить полученный статистический ряд графически;
3) вычислить выборочные характеристики: среднюю выборочную,
выборочную исправленную дисперсию, выборочное среднее
квадратическое отклонение, размах вариации, моду, медиану,
коэффициент вариации.
Решение.
1) Обозначим за X изучаемую случайную величину — Урожайность ржи.
Отметим, что эта величина непрерывного типа. Объем выборочной
совокупности n равен 50 (n=50).
Найдем 𝑥𝑚𝑖𝑛 , 𝑥𝑚𝑎𝑥 :
𝑥𝑚𝑖𝑛 = 10,7, 𝑥𝑚𝑎𝑥 = 26,3,
размах вариации
𝑅 = 𝑥𝑚𝑎𝑥 − 𝑥𝑚𝑖𝑛 ,
𝑅 = 15,6.
Для определения числа равных интервалов k, на которые следует разбить
весь диапазон значений случайной величины [𝑥𝑚𝑖𝑛 ; 𝑥𝑚𝑎𝑥 ], можно
пользоваться формулой
𝑘 = log 2 𝑛 + 1.
При этом следует учитывать, что число интервалов должно быть не
меньше 8-10 и не больше 20-25, 𝑛 ≥ 50.
Найдем ширину интервала группировки h:
𝑅
ℎ≈ .
𝑘
log 2 50 ≈ 5,6 4.
ℎ≈
15,6
≈ 2,35.
6,64
Для удобства вычислений возьмем h= 2,35.
Разобьем диапазон значений случайной величины [𝑥𝑚𝑖𝑛 ; 𝑥𝑚𝑎𝑥 ] на
классовые интервалы [𝑎𝑖−1 ; 𝑎𝑖 ], 𝑖 = 1,2, …
ℎ
𝑎0 = 𝑥𝑚𝑖𝑛 − ;
2
𝑎0 = 10,6 −
𝑎1 = 𝑎0 + ℎ;
𝑎1 = 9,425 + 2,35 = 11,775;
𝑎2 = 𝑎1 + ℎ;
𝑎2 = 11,775 + 2,35 = 14,125;
и т. д.
2,35
= 9,425;
2
Произведем разноску вариант по классовым интервалам с помощью
следующей таблицы.
i
1
2
3
4
5
6
7
8
[𝑎𝑖−1 ; 𝑎𝑖 )
[9,425; 11,775)
[11,775; 14,125)
[14,125; 16,475)
[16,475; 18,825)
[18,825; 21,175)
[21,175; 23,525)
[23,525; 25,875)]
[25,875; 28,225]
Разноска вариант
𝑥𝑖
10,6
12,95
15,3
17,65
20
22,35
24,7
27,05
𝑛𝑖
/
//
/////
///////////////
//////////
//////
//////
/////
1
2
5
15
10
6
6
5
i — номер интервала;
[𝑎𝑖−1 ; 𝑎𝑖 ) — классовые интервалы;
𝑥𝑖 — середины интервалов;
𝑛𝑖 — частоты.
Составим интервальный статистический ряд распределения
i
1
2
3
4
5
6
7
[𝒂𝒊−𝟏 ; 𝒂𝒊 )
[9,425; 11,775)
[11,775; 14,125)
[14,125; 16,475)
[16,475; 18,825)
[18,825; 21,175)
[21,175; 23,525)
[23,525; 25,875)]
2) Построим гистограмму
𝒙𝒊
𝒏𝒊
10,6
1
12,95
2
15,3
5
17,65
15
20
10
22,35
6
24,7
6
16
14
12
10
8
6
Series1
4
2
0
3) Вычислим числовые характеристики статистического ряда с помощью
следующей таблицы
i
1
𝒙𝒊
𝒏𝒊
𝒙𝒊 ∙ 𝒏𝒊
𝒙𝟐𝒊 ∙ 𝒏𝒊
𝑵𝒊
112,36
10,6
1
10,6
2
12,95
2
25,9
335,405
3
15,3
5
76,5
1170,45
4
17,65
15
264,75
4672,838
5
20
10
200
4000
6
22,35
6
134,1
2997,135
7
24,7
6
148,2
3660,54
8
27,05
5
135,25
3658,513
Σ
995,3
20607,24
𝑁𝑖 — накопленные частоты (𝑁1 = 𝑛1 , 𝑁2 = 𝑛1 + 𝑛2 , 𝑁3 = 𝑛1 + 𝑛2 + 𝑛3 , … ).
𝑥̅ — среднее выборочное,
𝑥̅ =
1
∑ 𝑥𝑖 ∙ 𝑛𝑖 ,
𝑛
𝑥̅ =
135,25
= 19,906,
50
𝑥̅ 2 = 19,9062 = 396,2488.
̅̅̅2 — среднее квадратов,
𝑥
̅̅̅2 = 1 ∑ 𝑥 2 ∙ 𝑛𝑖 ,
𝑥
𝑖
𝑛
̅̅̅2 = 20607,24 = 412,145.
𝑥
50
𝐷в — выборочная дисперсия,
̅̅̅2 − 𝑥̅ 2 ,
𝐷в = 𝑥
𝐷в = 412,145 − 396,2488 = 15,9.
1
3
8
23
33
39
45
50
𝑠 2 — исправленная выборочная дисперсия,
𝑠2 =
𝑛
𝐷,
𝑛−1 в
𝑠2 =
50
∗ 15,9 = 16,22.
49
𝑠 — исправленное выборочное среднее квадратическое отклонение,
𝑠 = √𝑠 2 ,
𝑠 = √16,22 = 4,03.
Вычислим числовые характеристики другим способом, с помощью
условных вариант.
Переходим к условным вариантам 𝑢𝑖 по формуле
𝑥𝑖 − 𝑑
𝑢𝑖 =
, 𝑖 = 1,2, … ,
ℎ
𝑑 — варианта с наибольшей частотой.
Возьмем 𝑑 = 17,65.
10,6 − 17,65
𝑢1 =
= −3,
2,35
12,95 − 17,65
𝑢2 =
= −2,
2,35
и т. д.
Вычислим числовые характеристики для условных вариант с помощью
следующей таблицы
𝒙𝒊
i
𝒏𝒊
𝒖𝒊
𝒖𝟐𝒊 ∙ 𝒏𝒊
𝒖 𝒊 ∙ 𝒏𝒊
1
2
3
4
5
6
7
10,6
12,95
15,3
17,65
20
22,35
24,7
-3
-2
-1
0
1
2
3
1
2
5
15
10
6
6
-3
-4
-5
0
10
12
18
9
8
5
0
10
24
54
4
2
2E-30
15
40
54
96
8
27,05
4
5
20
80
125
50
48
190
336
150,6
Контроль расчетов проводится по формуле
∑(𝑢𝑖 + 1)2 ∙ 𝑛𝑖 = ∑ 𝑢𝑖2 ∙ 𝑛𝑖 + 2 ∙ ∑ 𝑢𝑖 ∙ 𝑛𝑖 + ∑ 𝑛𝑖 ,
𝑖
(𝒖𝒊 + 𝟏)𝟐 ∙ 𝒏𝒊
𝑖
𝑖
336 = 190 + 2 ∗ 48 + 50 — верное равенство.
𝑖
𝑢̅ =
1
∑ 𝑢𝑖 ∙ 𝑛𝑖 ,
𝑛
𝑢̅ =
1
̅̅̅
𝑢2 = ∑ 𝑢𝑖2 ∙ 𝑛𝑖 ,
𝑛
𝐷𝑢 = ̅̅̅
𝑢2 − 𝑢̅2 ,
𝑠𝑢2 =
48
= 0,96,
50
𝑢̅2 = 0,9212.
190
̅̅̅
𝑢2 =
= 3,8
50
𝐷𝑢 = 3,8 − 0,9212 = 2,8788.
𝑛
𝐷 ,
𝑛−1 𝑢
𝑠𝑢2 =
50
∙ 2,8788 = 2,9376.
49
Переходим к числовым характеристикам основных вариант.
𝑥̅ = ℎ ∙ 𝑢̅ + 𝑑,
𝑥̅ = 2,35 ∗ 0,96 + 17,65 = 19,906
𝐷𝑥 = ℎ2 ∙ 𝐷𝑢 ,
𝐷𝑥 = 2,352 ∗ 2,8788 = 15,9.
𝑠𝑥2 = ℎ2 ∙ 𝑠𝑢2 ,
𝑠𝑥2 = 2,352 ∗ 2,9376 = 16,223.
𝑠𝑥 = √𝑠𝑥2 ,
𝑠𝑥 = √16,223 = 4,028.
Найдем моду по формуле
МО = 𝑥МО + ℎ ∙
𝑛2 − 𝑛1
.
(𝑛2 − 𝑛1 ) + (𝑛2 − 𝑛3 )
Модальный интервал № 4 (интервал с наибольшей частотой).
𝑥МО = 16,475(начало модального интервала),
𝑛2 = 15 (частота модального интервала),
𝑛1 = 5 (частота домодального интервала),
𝑛3 = 10 (частота замодального интервала),
h=2,35 (ширина интервала),
тогда мода равна
МО = 16,475 + 2,35 ∗
15 − 5
= 18,042.
(15 − 5) + (15 − 10)
Найдем медиану по формуле
𝑛
− 𝑛𝐻
2
Ме = 𝑥Ме + ℎ ∙
.
𝑛Ме
Медианный интервал № 3, так как его накопленная частота равна 23 и
𝑛
наиболее близка к числу = 25.
2
𝑥Ме = 16,475 (начало медианного интервала),
𝑛Ме = 15 (локальная частота медианного интервала),
𝑛𝐻 = 8 (накопленная частота интервала, предшествующего медианному),
𝑛
= 25,
2
ℎ = 2,35, тогда медиана равна
Ме = 16,475 + 2,35 ∗
25 − 8
= 19,138.
15
Коэффициент вариации
𝑉=
𝑠
4,028
∙ 100% =
∗ 100% = 20,24%.
𝑥̅
19,906
Изменчивость признака высокая (если 10%<V<20%, то изменчивость
признака средняя).
Задача 2 По данным задачи 1 требуется:
1) определить точечные оценки генеральной средней и генеральной
дисперсии генеральной совокупности;
2) определить доверительный интервал для оценки генеральной средней
при доверительной вероятности 𝛾 = 0,95;
3) найти вероятность того, что ошибка выборочной средней не превысит
величину a=1см;
4) найти необходимый объем выборки, чтобы с вероятностью 𝛾 = 0,99;
ошибка выборочной средней не превышала величину a=1см.
Решение.
1) Определим точечные оценки генеральной средней и генеральной
дисперсии генеральной совокупности:
𝑥̅Г ≈ 𝑥̅ = 19,906 см,
𝜎 2 ≈ 𝑠 2 = (4,028)2 = 16,225.
2) Если объем выборки достаточно большой (n>30), то распределение
выборочной средней 𝑥̅ , согласно центральной предельной теореме,
независимо от характера генерального распределения приближается к
нормальному распределению. Поскольку дисперсия генеральной
совокупности не известна и для ее оценки мы используем выборочную
исправленную дисперсию 𝑠 2 , то статистика
𝑇=
𝑥̅Г − 𝑥̅
𝑠
√𝑛
подчиняется закону распределения Стьюдента с 𝑘 = 𝑛 − 1 степенями
свободы. При больших значениях k (k>30) распределение Стьюдента
практически совпадает с нормированным нормальным распределением, т. е.
𝑇~𝑁(0, 1). Поэтому
𝑃(|𝑇| < 𝑡𝛾 ) = 2Φ(𝑡Υ ) = Υ ,
Υ = 0,95.
Решая уравнение
2Φ(𝑡Υ ) = Υ , 2Φ(𝑡Υ ) = 0,95,
Φ(𝑡Υ ) = 0,475,
находим 𝑡Υ = 1,96 по таблице функции Лапласа (приложение 2).
𝑃(|𝑇| < 𝑡𝛾 ) = 𝑃 (
|𝑥̅Г − 𝑥̅ |
𝑠
𝑠
<
𝑡
=
𝑃
−
𝑡
<
𝑥̅
<
𝑥̅
+
𝑡𝛾 ).
)
(𝑥̅
𝛾
𝛾
Г
𝑠
√𝑛
√𝑛
√𝑛
𝑠
𝑥̅ −
𝑥̅ +
√𝑛
𝑠
√𝑛
𝑠
√𝑛
𝑡𝛾 =
4,028
√50
∗ 1,96 = 1,111,
𝑡𝛾 = 19,906 − 1,111 = 18,795,
𝑡𝛾 = 19,906 + 1,111 = 21,017.
Итак, 𝑃(18,795 < 𝑥̅Г < 21,017) = 0,95.
Это означает, что с доверительной вероятностью 𝛾 = 0,95 доверительный
интервал (18,795 ; 21,017 )покрывает неизвестную генеральную среднюю 𝑥̅Г .
3) Требуется найти вероятность того, что ошибка выборочной средней
|𝑥̅Г − 𝑥̅ | не превысит величину a=1см.
Требуется найти
𝑃(|𝑥̅Г − 𝑥̅ | < 𝑎).
Найдем, используя формулу
𝑃 (|𝑥̅Г − 𝑥̅ | <
𝑠
√𝑛
∙ 𝑡𝛾 = 𝑎,
𝑡𝛾 =
𝑠
√𝑛
∙ 𝑡𝛾 ) = 2Φ(𝑡Υ ),
𝑎 ∙ √𝑛 1 ∗ √50
=
= 1,775,
𝑠
4,028
2Φ(𝑡Υ ) = 2Φ(1,775) = 2 ∗ 0,4625 = 0,925.
Вероятность того, что ошибка выборочной средней не превысит величину
a=1см, равна 0,925.
4) Используем формулу
𝑃 (|𝑥̅Г − 𝑥̅ | <
𝑠
√𝑛
∙ 𝑡𝛾 ) = 2Φ(𝑡Υ ) = Υ ,
Υ = 0,99.
Тогда
2Φ(𝑡Υ ) = 0,99, Φ(𝑡Υ ) = 0,495,
𝑡Υ = 2,58 (по таблице функции Лапласа (приложение 2))
𝑠
√𝑛
∙ 𝑡𝛾 = 𝑎,
√𝑛 =
𝑠
4,028
∙ 𝑡𝛾 =
∗ 2,58 = 10,39,
𝑎
1
𝑛 = 107,99.
Следует взять 𝑛 = 108 (целое и больше 224,3).
Объем выборки должен быть не менее 𝑛 = 108, чтобы ошибка выборочной
средней не превышала a=1см с вероятностью 𝛾 = 0,99.
Задача 3
Требуется по данным задачи 1 построить полигон наблюдаемых частот и
нормальную (теоретическую) кривую по выравнивающим частотам.
Решение. Вычисление выравнивающих частот 𝑦𝑖 произведем с помощью
таблицы
𝒙𝒊
1
2
3
4
5
6
7
166
170
174
178
182
186
190
𝑥𝑖 −𝑥̅
𝑢𝑖 =
𝑠
𝜑(𝑥) =
𝑦𝑖 =
i
𝑛∙ℎ
𝑠
𝒏𝒊
4
11
10
19
7
3
2
𝒖𝒊
𝝋(𝒖𝒊 )
𝒚𝒊
−1,76
−1,07
−0,38
0,31
1
1,69
2,38
0,0848
0,2251
0,3712
0,3802
0,2420
0,0957
0,0235
3,3
8,7
14,3
14,7
9,3
3,7
0,9
,
1
√2𝜋
𝑒
𝑥2
2
−
, 𝜑(−𝑥) = 𝜑(𝑥) (значения функции смотри в приложении 1),
∙ 𝜑(𝑢𝑖 ) — выравнивающие частоты.
Строим полигон наблюдаемых частот (по 𝑛𝑖 ) и нормальную теоретическую
кривую (по 𝑦𝑖 ), имеющую 𝜇 = 𝑥̅ и 𝜎 = 𝑠.
20
18
16
14
12
10
8
6
4
2
0
n
y
166
170
174
178
182
186
190
Видим, что полигон наблюдаемых частот близок к нормальной кривой.
Задача 4
По данным задачи 1 при уровне значимости 𝛼 = 0,05 проверить гипотезу о
нормальном распределении признака с помощью критерия Пирсона.
Решение.
Нулевая (выдвигаемая) гипотеза заключается в том, что признак X (рост
новобранца) распределен по нормальному закону. Проверим ее.
Объем выборки должен быть не менее 50. Каждая интервальная группа
должна содержать не менее 5-8 вариант. Малочисленные группы следует
объединять, при этом частоты суммируются.
Вычислим наблюдаемое значение
𝜒Н2
=∑
(𝑛𝑖 −𝑛𝑖∗ )
2
𝑛𝑖∗
(хи квадрат) с помощью
таблицы. Предварительно рассмотрим статистический ряд распределения и
малочисленные интервалы объединим: 1 и 2, 6 и 7, частоты суммируем.
𝑎𝑖∗ =
𝑎𝑖 − 𝑥̅
,
𝑠
Φ(𝑎𝑖∗ ) — значения функции Лапласа (смотри приложение 2),
∗
),
𝑝𝑖 = Φ(𝑎𝑖∗ ) − Φ(𝑎𝑖−1
𝑛𝑖∗ = 𝑝𝑖 ∙ 𝑛.
𝒂𝒊∗
𝚽(𝒂∗𝒊−𝟏 )
𝚽(𝒂∗𝒊 )
𝒑𝒊
𝒏∗𝒊
(𝒏𝒊 − 𝒏∗𝒊 )𝟐
𝒏∗𝒊
i
𝒏𝒊
𝒂𝒊−𝟏
𝒂𝒊
∗
𝒂𝒊−𝟏
1
15
164
172
−2,10
−0,72
−0,4821
−0,2642
0,2179
12,20
0,64
2
10
172
176
−0,72
−0,03
−0,2642
−0,0120
0,2522
14,12
1,20
3
19
176
180
−0,03
0,65
−0,0120
0,2422
0,254
14,22
1,61
4
7
180
184
0,65
1,34
0,2422
0,4099
0,1677
9,39
0,61
5
5
184
192
1,34
2,72
0,4099
0,4967
0,0868
4,86
0,00
∑ = 𝟒, 𝟎𝟔
Наблюдаемое значение критерия 𝜒Н2 = 4.06.
2
Критическая область определяется неравенством 𝜒Н2 > 𝜒кр
.
Число интервалов 𝑚 = 5,
число степеней свободы 𝑘 = 𝑚 − 3 = 5 − 3 = 2,
уровень значимости 𝛼 = 0,05,
2
𝜒кр.
= 6 (смотри приложение 3).
Наблюдаемое значение критерия не попадает в критическую область,
следовательно, нет оснований отвергать гипотезу о нормальном
распределении признака на заданном уровне значимости.