Вариант x Задание x

2
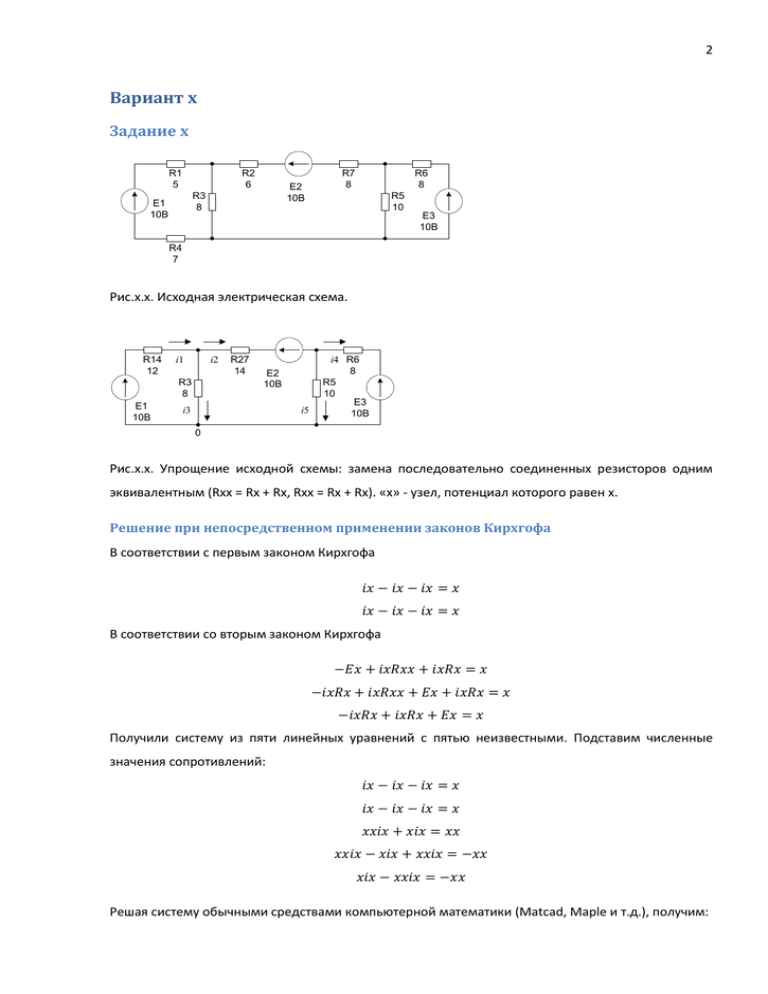
Вариант x
Задание x
R1
5
R2
6
E2
10В
R3
8
E1
10В
R7
8
R6
8
R5
10
E3
10В
R4
7
Рис.x.x. Исходная электрическая схема.
R14
12
i1
i2
R3
8
E1
10В
R27
14
E2
10В
i3
i5
i4 R6
8
R5
10
E3
10В
0
Рис.x.x. Упрощение исходной схемы: замена последовательно соединенных резисторов одним
эквивалентным (Rxx = Rx + Rx, Rxx = Rx + Rx). «x» - узел, потенциал которого равен x.
Решение при непосредственном применении законов Кирхгофа
В соответствии с первым законом Кирхгофа
𝑖𝑥 − 𝑖𝑥 − 𝑖𝑥 = 𝑥
𝑖𝑥 − 𝑖𝑥 − 𝑖𝑥 = 𝑥
В соответствии со вторым законом Кирхгофа
−𝐸𝑥 + 𝑖𝑥𝑅𝑥𝑥 + 𝑖𝑥𝑅𝑥 = 𝑥
−𝑖𝑥𝑅𝑥 + 𝑖𝑥𝑅𝑥𝑥 + 𝐸𝑥 + 𝑖𝑥𝑅𝑥 = 𝑥
−𝑖𝑥𝑅𝑥 + 𝑖𝑥𝑅𝑥 + 𝐸𝑥 = 𝑥
Получили систему из пяти линейных уравнений с пятью неизвестными. Подставим численные
значения сопротивлений:
𝑖𝑥 − 𝑖𝑥 − 𝑖𝑥 = 𝑥
𝑖𝑥 − 𝑖𝑥 − 𝑖𝑥 = 𝑥
𝑥𝑥𝑖𝑥 + 𝑥𝑖𝑥 = 𝑥𝑥
𝑥𝑥𝑖𝑥 − 𝑥𝑖𝑥 + 𝑥𝑥𝑖𝑥 = −𝑥𝑥
𝑥𝑖𝑥 − 𝑥𝑥𝑖𝑥 = −𝑥𝑥
Решая систему обычными средствами компьютерной математики (Matcad, Maple и т.д.), получим:
3
𝑖𝑥 = 𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = −𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = −𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝑥, 𝑥𝑥𝑥 А
Знак «–» означает, что действительное направление тока не совпадает с произвольно выбранным.
Решение методом контурных токов
E1
10В
R14
12
R27
14
E2
10В
R3
8
I1
I2
R6
8
R5
10
E3
10В
I3
0
Рис.x.x. Упрощенная схема с указанием контурных токов.
Как показано на рис.x, в схеме x контура, соответственно число уравнений сокращается с x в
предыдущем случае до x, что существенно упрощает вычислительный процесс.
Контурные токи связаны с действительными токами следующим образом:
𝑖𝑥 = 𝐼𝑥
𝑖𝑥 = 𝐼𝑥
𝑖𝑥 = 𝐼𝑥 − 𝐼𝑥
𝑖𝑥 = 𝐼𝑥
𝑖𝑥 = 𝐼𝑥 − 𝐼𝑥
Запишем контурные уравнения:
−𝐸𝑥 + 𝐼𝑥𝑅𝑥𝑥 + (𝐼𝑥 − 𝐼𝑥)𝑅𝑥 = 𝑥
(𝐼𝑥 − 𝐼𝑥)𝑅𝑥 + 𝐼𝑥𝑅𝑥𝑥 + 𝐸𝑥 + (𝐼𝑥 − 𝐼𝑥)𝑅𝑥 = 𝑥
(𝐼𝑥 − 𝐼𝑥)𝑅𝑥 + 𝐼𝑥𝑅𝑥 + 𝐸𝑥 = 𝑥
Или
𝑥𝑥𝐼𝑥 − 𝑥𝐼𝑥 = 𝑥𝑥
−𝑥𝐼𝑥 + 𝑥𝑥𝐼𝑥 − 𝑥𝑥𝐼𝑥 = −𝑥𝑥
−𝑥𝑥𝐼𝑥 + 𝑥𝑥𝐼𝑥 = −𝑥𝑥
Решение такой системы:
𝐼𝑥 = 𝑥, 𝑥𝑥𝑥 А
𝐼𝑥 = −𝑥, 𝑥𝑥𝑥 А
𝐼𝑥 = −𝑥, 𝑥𝑥𝑥 А
4
Окончательно получаем:
𝑖𝑥 = 𝐼𝑥 = 𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝐼𝑥 = −𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝐼𝑥 − 𝐼𝑥 = 𝑥, 𝑥𝑥𝑥 − (−𝑥, 𝑥𝑥𝑥) = 𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝐼𝑥 = −𝑥, 𝑥𝑥𝑥 А
𝑖𝑥 = 𝐼𝑥 − 𝐼𝑥 = −𝑥, 𝑥𝑥𝑥— 𝑥, 𝑥𝑥𝑥 = 𝑥, 𝑥𝑥𝑥 А
Как видно, второй способ решения – по методу контурных токов – является менее трудоемким,
чем решение с непосредственным использованием законов Кирхгофа.
5
Задание x
i1
U
220В 50Гц
L1
0,6 Гн
C1
10 мкФ
R1
20 Ом
C2
15 мкФ
R2
30 Ом
i2
i3
L2
1,0 Гн
Рис.x.x. Схема цепи переменного тока.
Решение
Полный импеданс цепи (между входными зажимами) равен:
𝑍 = 𝑅𝑥 − 𝑗𝑋𝐶𝑥 + 𝑗𝑋𝐿𝑥 + 𝑍||
Здесь импеданс двух параллельно включенных ветвей
𝑥
𝑍|| =
𝑥
𝑥
𝑅𝑥 − 𝑗𝑋𝐶𝑥 + 𝑗𝑋𝐿𝑥
Реактивные сопротивления при  = xf = xxx,x рад/с:
𝑥
𝑥
𝑋𝐶𝑥 =
=
= 𝑥𝑥𝑥, 𝑥 Ом
𝜔𝐶𝑥 𝑥𝑥𝑥, 𝑥 ∙ 𝑥𝑥 −𝑥
𝑥
𝑥
𝑋𝐶𝑥 =
=
= 𝑥𝑥𝑥, 𝑥 Ом
𝜔𝐶𝑥 𝑥𝑥𝑥, 𝑥 ∙ 𝑥, 𝑥 ∙ 𝑥𝑥 −𝑥
𝑋𝐿𝑥 = 𝜔𝐿𝑥 = 𝑥𝑥𝑥, 𝑥 ∙ 𝑥, 𝑥 = 𝑥𝑥𝑥, 𝑥 Ом
𝑋𝐿𝑥 = 𝜔𝐿𝑥 = 𝑥𝑥𝑥, 𝑥 ∙ 𝑥 = 𝑥𝑥𝑥, 𝑥 Ом
Получаем:
𝑍|| =
𝑥
𝑥
𝑥 = 𝑥𝑥𝑥, 𝑥 − 𝑗𝑥𝑥𝑥, 𝑥 Ом
+
𝑥𝑥 − 𝑗𝑥𝑥𝑥, 𝑥 𝑗𝑥𝑥𝑥, 𝑥
𝑍 = 𝑥𝑥 − 𝑗𝑥𝑥𝑥, 𝑥 + 𝑗𝑥𝑥𝑥, 𝑥 + 𝑥𝑥𝑥, 𝑥 − 𝑗𝑥𝑥𝑥, 𝑥 = 𝑥𝑥𝑥, 𝑥 − 𝑗𝑥𝑥𝑥, 𝑥 Ом
Теперь можно вычислить ток ix:
𝑖𝑥 =
𝑈
𝑥𝑥𝑥
=
= 𝑥, 𝑥𝑥 + 𝑗𝑥, 𝑥𝑥 А = 𝑥, 𝑥𝑥𝑒 𝑗𝑥,𝑥𝑥 А
𝑍 𝑥𝑥𝑥, 𝑥 − 𝑗𝑥𝑥𝑥, 𝑥
Замечание x: в экспоненциальной форме угол указан в радианах.
Падение напряжения на параллельно включенных ветвях:
𝑈|| = 𝑖𝑥𝑍|| = (𝑥, 𝑥𝑥 + 𝑗𝑥, 𝑥𝑥)(𝑥𝑥𝑥, 𝑥 − 𝑗𝑥𝑥𝑥, 𝑥) = 𝑥𝑥𝑥, 𝑥 + 𝑗𝑥, 𝑥 В = 𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥 В
Ток ix равен:
𝑖𝑥 =
𝑈||
𝑥𝑥𝑥, 𝑥 + 𝑗𝑥, 𝑥
=
= 𝑥, 𝑥𝑥 − 𝑗𝑥, 𝑥𝑥 А = 𝑥, 𝑥𝑥𝑒 −𝑗𝑥,𝑥𝑥 А
𝑗𝑋𝐿𝑥
𝑗𝑥𝑥𝑥, 𝑥
6
В соответствии с первым законом Кирхгофа
𝑖𝑥 = 𝑖𝑥 − 𝑖𝑥 = 𝑥, 𝑥𝑥 + 𝑗𝑥, 𝑥𝑥 − (𝑥, 𝑥𝑥 − 𝑗𝑥, 𝑥𝑥) = 𝑥, 𝑥𝑥 + 𝑗𝑥, 𝑥𝑥 А = 𝑥, 𝑥𝑥𝑒 𝑗𝑥,𝑥𝑥 А
Замечание x: элементы Rx, Cx и Lx образуют параллельный колебательный контур, токи в ветвях
которого могут быть существенно больше, чем суммарный ток через контур. Этим и объясняется
то, что действующие значения токов ix и ix больше, чем ток ix.
7
Задание x
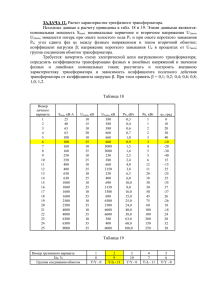
Результаты испытаний однофазного трансформатора:
Uxном, В
Uxном, В
Ixном, А
UК , В
IХ, А
PХ, Вт
PК, Вт
xxxx
xxx
x,x
xxx
x,xx
xx
xxx
Решение
1. Коэффициент трансформации равен:
𝑘=
𝑈𝑥ном
𝐸𝑥
ЭДС холостого хода Ex отличается от напряжения Uxном на величину падения напряжения на
активном и индуктивном сопротивлении вторичной обмотки:
𝐸𝑥 = 𝑈𝑥ном + 𝐼𝑥ном 𝑍𝑥ном
Ввиду того, что импеданс обмоток носит комплексный характер, для определения коэффициента
трансформации в формулу для k нужно подставить модули (действующие значения):
𝑘=
|𝑈𝑥ном |
𝑈𝑥ном
=
|𝐸𝑥 |
|𝑈𝑥ном + 𝐼𝑥ном 𝑍𝑥ном |
Для вычисления импеданса на основе измеренных данных нужно сначала определить
коэффициент мощности в режиме короткого замыкания.
2. Коэффициент мощности в режиме короткого замыкания определим из выражения для
мощности потерь:
𝑃К = 𝑈К 𝐼𝑥ном cos 𝜑К
Тогда
cos 𝜑К =
𝑃К
𝑥𝑥𝑥
=
= 𝑥, 𝑥𝑥
𝑈К 𝐼𝑥ном 𝑥𝑥𝑥 ∙ 𝑥, 𝑥
Соответственно
𝜑К = arccos 𝑥, 𝑥𝑥 = 𝑥, 𝑥𝑥 рад
Аналогично находим коэффициент мощности в режиме холостого хода:
cos 𝜑Х =
𝑃Х
𝑈𝑥ном 𝐼Х
=
𝑥𝑥
= 𝑥, 𝑥𝑥𝑥
𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥𝑥
𝜑Х = arccos 𝑥, 𝑥𝑥𝑥 = 𝑥, 𝑥𝑥 рад
3. При измерении в режиме короткого замыкания токи в обмотках не превышают номинального
значения, то есть магнитное состояние сердечника трансформатора соответствует
номинальному режиму (нет насыщения сердечника). Следовательно, из импеданса при
коротком замыкании можно определить импеданс вторичной обмотки при номинальном
режиме:
𝑍𝑥 =
𝑍К
𝑥𝑘 𝑥
8
Здесь
𝑍К =
𝑈К
𝐼𝑥ном
𝑒 𝑗𝜑К =
𝑥𝑥𝑥 𝑗𝑥,𝑥𝑥
𝑒
= 𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥 Ом = 𝑥𝑥, 𝑥 + 𝑗𝑥𝑥𝑥, 𝑥 Ом
𝑥, 𝑥
Множитель «x» в выражении для Zx означает, что приведенные импедансы первичной и
вторичной обмоток равны:
𝑍К
𝑍𝑥 = 𝑘 𝑥 𝑍𝑥 =
𝑥
4. Теперь можно записать уравнение для определения коэффициента трансформации, учитывая
ток холостого хода:
𝑘=
𝑈𝑥ном
𝑈𝑥ном
=
=
|𝑈𝑥ном + 𝐼𝑥ном 𝑍𝑥ном | |𝑈𝑥ном + (𝐼𝑥ном − 𝐼Х )𝑘𝑍𝑥ном | |𝑈
𝑥ном
𝑈𝑥ном
+ (𝐼𝑥ном − 𝐼Х )𝑘
𝑈𝑥ном
=
|𝑈𝑥ном + (𝐼𝑥ном − 𝐼Х )
𝑍К
𝑥𝑘 𝑥 |
𝑍К
|
𝑥𝑘
Подставим известные численные значения:
𝑥𝑥𝑥𝑥
𝑘=
|𝑥𝑥𝑥 + (𝑥, 𝑥 − 𝑥, 𝑥𝑥)
𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥
|
𝑥𝑘
Или:
𝑘=
𝑥𝑥𝑘
√𝑥, 𝑥𝑥𝑘 𝑥 + 𝑥, 𝑥𝑥𝑘 + 𝑥, 𝑥𝑥𝑥
Корни уравнения:
𝑘 = {𝑥; −𝑥𝑥, 𝑥; 𝑥𝑥, 𝑥𝑥}
Выбираем положительный ненулевой корень:
𝑘 = 𝑥𝑥, 𝑥𝑥
При этом действующее значение эдс вторичной обмотки равно
𝐸𝑥 = |𝑥𝑥𝑥 + (𝑥, 𝑥 − 𝑥, 𝑥𝑥)
𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥
| = |𝑥𝑥𝑥, 𝑥 + 𝑗𝑥, 𝑥𝑥| = 𝑥𝑥𝑥, 𝑥 В
𝑥 ∙ 𝑥𝑥, 𝑥𝑥
Сравним полученное значение с приближенным, когда не учитывается падение напряжения на
вторичной обмотке:
𝑈𝑥ном 𝑥𝑥𝑥𝑥
𝑘~ =
=
= 𝑥𝑥, 𝑥𝑥
𝑈𝑥ном
𝑥𝑥𝑥
Отличие составляет x,xx%.
5. Рассчитаем активные и реактивные составляющие импедансов первичной и вторичной
обмоток.
Импеданс первичной обмотки равен
9
𝑍𝑥 =
𝑍К 𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥
=
= 𝑥𝑥, 𝑥 + 𝑗𝑥𝑥, 𝑥 Ом
𝑥
𝑥
Соответственно активное и индуктивное сопротивления первичной обмотки равны
𝑅𝑥 = 𝐑𝐞 (𝑍𝑥 ) = 𝑥𝑥, 𝑥 Ом
𝑋𝑥 = 𝐈𝐦 (𝑍𝑥 ) = 𝑥𝑥, 𝑥 Ом
Импеданс вторичной обмотки равен
𝑍𝑥 =
𝑍К
𝑥𝑥𝑥, 𝑥𝑒 𝑗𝑥,𝑥𝑥
=
= 𝑥, 𝑥𝑥 + 𝑗𝑥, 𝑥𝑥 Ом
𝑥𝑘 𝑥
𝑥 ∙ 𝑥𝑥, 𝑥𝑥 𝑥
Соответственно активное и индуктивное сопротивления вторичной обмотки равны
𝑅𝑥 = 𝐑𝐞 (𝑍𝑥 ) = 𝑥, 𝑥𝑥 Ом
𝑋𝑥 = 𝐈𝐦 (𝑍𝑥 ) = 𝑥, 𝑥𝑥 Ом
6. Определим максимальный и номинальный кпд трансформатора, то есть отношение активной
мощности, отдаваемой в нагрузку,
𝑃𝑥 = 𝛽𝑆ном cos 𝜑𝑥
к активной мощности, к активной мощности, потребляемой из сети:
𝑥
𝑃𝑥 = 𝑃𝑥 + 𝑃Х + 𝛽 𝑃К
Здесь Sном – полная мощность трансформатора при номинальной нагрузке, cosx – коэффициент
мощности нагрузки,  – коэффициент нагрузки трансформатора:
𝑆ном = 𝑈𝑥ном 𝐼𝑥ном = 𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥 = 𝑥𝑥𝑥𝑥𝑥 ВА
𝛽=
𝐼𝑥
𝐼𝑥ном
Коэффициент мощности нагрузки принимаем равным x,xx (в соответствии с литературными
данными cosx = x,x…x,x).
При номинальной нагрузке  = x и
𝜂=
𝑃𝑥
𝛽𝑆ном cos 𝜑𝑥
𝑥𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥𝑥
=
=
= 𝑥, 𝑥𝑥
𝑥
𝑃𝑥 𝛽𝑆ном cos 𝜑𝑥 + 𝑃Х + 𝛽 𝑃К 𝑥𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥𝑥 + 𝑥𝑥 + 𝑥𝑥𝑥
Трансформатор имеет максимальный кпд при значении коэффициента нагрузки, равного
𝑃Х
𝑥𝑥
=√
= 𝑥, 𝑥𝑥𝑥
𝑃К
𝑥𝑥𝑥
𝛽=√
При этом
𝜂max =
𝑥, 𝑥𝑥𝑥 ∙ 𝑥𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥𝑥
= 𝑥, 𝑥𝑥
𝑥, 𝑥𝑥𝑥 ∙ 𝑥𝑥𝑥𝑥𝑥 ∙ 𝑥, 𝑥𝑥 + 𝑥𝑥 + 𝑥, 𝑥𝑥𝑥 𝑥 ∙ 𝑥𝑥𝑥
10
Задание x
Параметры асинхронного электродвигателя:








номинальное линейное напряжение трехфазной сети Ux = xxx В;
мощность на валу Px = xxxx Вт;
частота вращения ротора nx = xxxx об/мин;
кпд  = xx%;
коэффициент мощности cos  = x,x;
кратность пускового тока KП = x,x;
кратность пускового момента KМ = x,xx;
коэффициент перегрузочной способности  = x,xx.
Решение
1. Ближайшее к частоте вращения ротора значение частоты вращения магнитного поля (при
частоте сети xx Гц) составляет
𝑛𝑥 =
𝑥𝑥𝑓𝑥 𝑥𝑥 ∙ 𝑥𝑥
об
=
= 𝑥𝑥𝑥𝑥
𝑝
𝑥
мин
Число пар полюсов для этой частоты равно
𝑝=𝑥
Номинальное скольжение определим из формулы
𝑛𝑥 =
𝑥𝑥𝑓𝑥
(𝑥 − 𝑠)
𝑝
То есть
𝑠ном = 𝑥 −
𝑛𝑥
𝑥𝑥𝑥𝑥
=𝑥−
= 𝑥, 𝑥𝑥
𝑛𝑥
𝑥𝑥𝑥𝑥
Критическое скольжение равно:
𝑠кр = 𝑠ном (𝜆 + √𝜆𝑥 − 𝑥) = 𝑥, 𝑥𝑥(𝑥, 𝑥𝑥 + √𝑥, 𝑥𝑥 𝑥 − 𝑥) = 𝑥, 𝑥𝑥
2. Номинальный вращающий момент на валу двигателя:
𝑀ном = 𝑥, 𝑥𝑥
𝑃𝑥
𝑥𝑥𝑥𝑥
н
н
= 𝑥, 𝑥𝑥
= 𝑥𝑥, 𝑥𝑥 ≈ 𝑥𝑥, 𝑥
𝑛𝑥
𝑥𝑥𝑥𝑥
м
м
Пусковой вращающий момент на валу двигателя:
𝑀пуск = 𝑀ном 𝐾М = 𝑥𝑥, 𝑥𝑥 ∙ 𝑥, 𝑥𝑥 = 𝑥𝑥, 𝑥𝑥
н
н
≈ 𝑥𝑥, 𝑥
м
м
3. Для определения номинального и пускового тока сначала вычислим активную мощность Px,
потребляемую из сети:
𝑃𝑥 𝑥𝑥𝑥𝑥
𝑃𝑥 = =
= 𝑥𝑥𝑥𝑥 Вт
𝜂
𝑥, 𝑥𝑥
Фазный ток в обмотке статора равен
𝑃𝑥
𝐼𝑥Ф =
𝑥𝑈𝑥Ф cos 𝜑
11
Здесь
𝑈𝑥Ф =
𝑈𝑥
√𝑥
=
𝑥𝑥𝑥
= 𝑥𝑥𝑥 В
𝑥, 𝑥𝑥𝑥
Получаем значение тока в номинальном режиме:
𝐼𝑥Фном =
𝑥𝑥𝑥𝑥
= 𝑥, 𝑥𝑥 А
𝑥 ∙ 𝑥𝑥𝑥 ∙ 𝑥, 𝑥
Пусковой ток равен:
𝐼𝑥Фпуск = 𝐼𝑥Фном 𝐾П = 𝑥, 𝑥𝑥 ∙ 𝑥, 𝑥 = 𝑥𝑥, 𝑥 А
12
Задание x
Тр
U2(2)
U1
U2(2)
VD1
R
VD2
Рис.x.x. Однофазный двухполупериодный выпрямитель со средней точкой.
Заданные параметры:



напряжение сети Ux = xxx В;
среднее напряжение на нагрузке Uср = xx В;
сопротивление нагрузки R = x Ом.
Решение
1. Расчетная мощность трансформатора:
𝑆Т = 𝑥, 𝑥𝑥𝑃ном нагр = 𝑥, 𝑥𝑥
𝑥
𝑈ср
𝑥𝑥 𝑥
= 𝑥, 𝑥𝑥
= 𝑥𝑥𝑥 Вт
𝑅
𝑥
2. Площадь сечения сердечника трансформатора:
𝑄 = 𝑥, 𝑥√𝑆Т = 𝑥, 𝑥 √𝑥𝑥𝑥 = 𝑥𝑥, 𝑥 см𝑥
3. Требуемый коэффициент трансформации равен
𝐾Т =
𝑈𝑥
𝑈𝑥
Здесь
𝑈𝑥 =
𝑈ср
𝑥𝑥
=
= 𝑥𝑥, 𝑥 В
𝑥, 𝑥 𝑥, 𝑥
Получаем:
𝑥𝑥𝑥
= 𝑥𝑥, 𝑥
𝑥𝑥, 𝑥
4. Действующее значение тока первичной обмотки трансформатора:
𝐾Т =
𝐼𝑥 =
𝜋 𝐼ср
𝑥√𝑥 𝐾Т
Здесь
𝐼ср =
𝑈ср 𝑥𝑥
=
=𝑥А
𝑅
𝑥
Получаем:
𝐼𝑥 =
𝑥, 𝑥𝑥
𝑥
∙
= 𝑥, 𝑥𝑥𝑥 А
𝑥 ∙ 𝑥, 𝑥𝑥 𝑥𝑥, 𝑥
Действующее значение тока вторичной обмотки трансформатора:
𝐼𝑥 =
𝜋
𝑥, 𝑥𝑥
𝐼ср =
𝑥 = 𝑥, 𝑥𝑥 А
𝑥
𝑥
13
5. Диаметр провода первичной обмотки трансформатора:
𝐼𝑥
𝑥, 𝑥𝑥𝑥
𝑑𝑥 = 𝑥, 𝑥𝑥√ = 𝑥, 𝑥𝑥√
= 𝑥, 𝑥𝑥𝑥 мм
𝑥
𝑥
Диаметр провода вторичной обмотки трансформатора:
𝐼𝑥
𝑥, 𝑥𝑥
𝑑𝑥 = 𝑥, 𝑥𝑥√ = 𝑥, 𝑥𝑥√
= 𝑥, 𝑥𝑥 мм
𝑥
𝑥
6. Действующее значение тока вентиля равно:
𝐼вент = 𝐼𝑥 =
𝜋
𝑥, 𝑥𝑥
𝐼ср =
𝑥 = 𝑥, 𝑥𝑥 А
𝑥
𝑥
Максимальное значение тока вентиля равно:
𝐼вент макс = 𝑥, 𝑥𝑥𝐼ср = 𝑥, 𝑥𝑥 ∙ 𝑥 = 𝑥, 𝑥𝑥 А
7. Максимальное обратное напряжение на вентиле равно:
𝑈обр макс = 𝑥√𝑥𝑈𝑥 = 𝑥 ∙ 𝑥, 𝑥𝑥 ∙ 𝑥𝑥, 𝑥 = 𝑥𝑥, 𝑥 В