а = 0, а

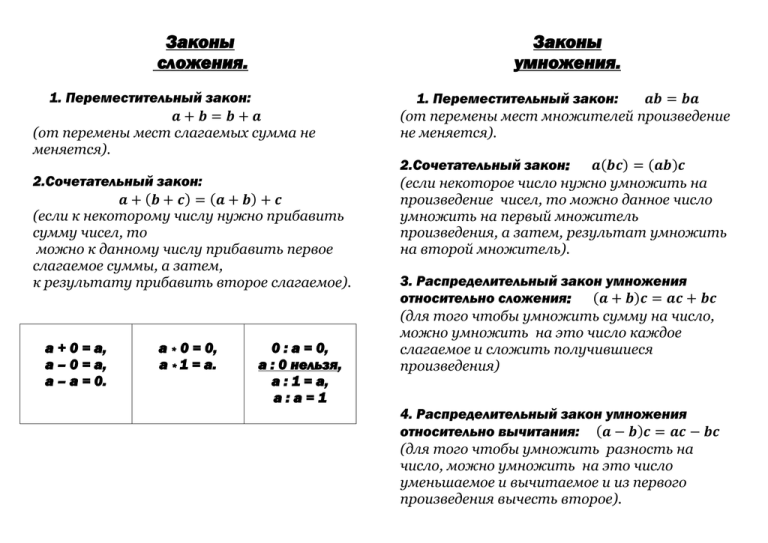
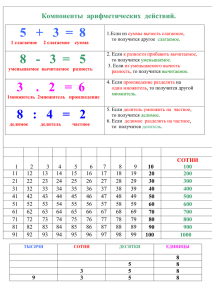
Законы
сложения.
Законы
умножения.
1. Переместительный закон:
𝒂+𝒃=𝒃+𝒂
(от перемены мест слагаемых сумма не
меняется).
2.Сочетательный закон:
𝒂 + (𝒃 + 𝒄) = (𝒂 + 𝒃) + 𝒄
(если к некоторому числу нужно прибавить
сумму чисел, то
можно к данному числу прибавить первое
слагаемое суммы, а затем,
к результату прибавить второе слагаемое).
а + 0 = а,
а – 0 = а,
а – а = 0.
а * 0 = 0,
а * 1 = а.
0 : а = 0,
а : 0 нельзя,
а : 1 = а,
а:а=1
1. Переместительный закон:
𝒂𝒃 = 𝒃𝒂
(от перемены мест множителей произведение
не меняется).
2.Сочетательный закон:
𝒂(𝒃𝒄) = (𝒂𝒃)𝒄
(если некоторое число нужно умножить на
произведение чисел, то можно данное число
умножить на первый множитель
произведения, а затем, результат умножить
на второй множитель).
3. Распределительный закон умножения
(𝒂 + 𝒃)𝒄 = 𝒂𝒄 + 𝒃𝒄
относительно сложения:
(для того чтобы умножить сумму на число,
можно умножить на это число каждое
слагаемое и сложить получившиеся
произведения)
4. Распределительный закон умножения
относительно вычитания: (𝒂 − 𝒃)𝒄 = 𝒂𝒄 − 𝒃𝒄
(для того чтобы умножить разность на
число, можно умножить на это число
уменьшаемое и вычитаемое и из первого
произведения вычесть второе).
Компоненты
действий.
разряды
десятки
единицы
2
1
5
3
8
9
0
0
7
4
6
2
25 – ? = 13
? – 12 = 13
число
25 – 13 = 12
13 + 12 = 25
Аксиомы натуральных чисел.
IY. Деление.
50 : ? = 2
? : 25 = 2
50 : 2 = 25
25 · 2 = 50
единицы
сотни
тысячи
единицы
миллионы
десятки
миллиарды
сотни
III. Вычитание.
классы
единицы
50 : 25 = 2
десятки
25 - 13 = 12
это тысяча миллионов,
1 млрд. = 1 000 000 000.
сотни
25* ? = 50
единицы
13 + ? = 25
десятки
II. Умножение.
сотни
I. Сложение.
это тысяча тысяч,
1 млн. = 1 000 000.
 Числа, используемые для счета предметов,
называются натуральными.
 Самое маленькое натуральное число – единица.
 В натуральном ряду каждое следующее число
на 1 больше предыдущее
 Не существует самого большого натурального
числа.
 Нуль не относится к натуральным числам.
Названия компонентов при сложении:
1 слагаемое, 2 слагаемое, сумма.
Суммой называют не только результат, но и само выражение .
2+3=5
2 - первое слагаемое
3 - второе слагаемое
5 - сумма
2 + 3 - сумма
Чтобы найти неизвестное слагаемое надо из суммы вычесть
известное слагаемое.
Названия компонентов при вычитании:
уменьшаемое, вычитаемое, разность.
Разностью называют не только результат действия, но и само
выражение.
8-3=5
8 - уменьшаемое
3 - вычитаемое
5 - разность
8 - 3 - разность
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
Названия компонентов при умножении:
множитель, множитель, произведение.
Произведением называют не только результат действия, но и само
выражение.
8 х 3 = 24
8 - множитель
3 - множитель
24 - произведение
8 х 3 - произведение
Чтобы найти неизвестный множитель, надо произведение разделить
на известный множитель (24:8=3)
Названия компонентов при делении:
делимое, делитель, частное.
Частным называют не только результат действия, но и само
выражение.
8:2=4
8 - делимое
2 - делитель
4 - частное
8 : 4 - частное
Чтобы найти делимое, надо частное умножить на делитель (4х2=8)
Чтобы найти делитель, надо делимое разделить на частное (8:4=2)
Уравнение.
Уравнением с одной переменной, называется
равенство, содержащее только одну переменную.
Корнем (или решением) уравнения называется
такое значение переменной, при котором уравнение
превращается в верное числовое равенство.
Найти все корни уравнения или доказать, что
их нет – это значит решить уравнение.
Свойство 1. При переносе слагаемого из одной части
уравнения в другую с противоположным знаком, получается
уравнение с теми же корнями.
x–3=6
x=6+3
x=9.
Свойство 2. При умножении или делении обеих
частей уравнения на одно и то же число, отличное от нуля,
мы получим уравнение с теми же корнями (решениями).
3x = 6
3x : 3 = 6 : 3
x=2.
Алгоритм решения уравнения
1. Перенести члены, содержащие
переменную, в одну часть, а свободные
(без переменной) в другую часть.
2. Привести подобные слагаемые (сложить
коэффициенты при переменной).
3. Обе части уравнения разделить на
коэффициент при х и найти корень
уравнения.