Анализ КДР по математике 9 класс 18.02.2015 Целью процесса подготовки к ГИА.

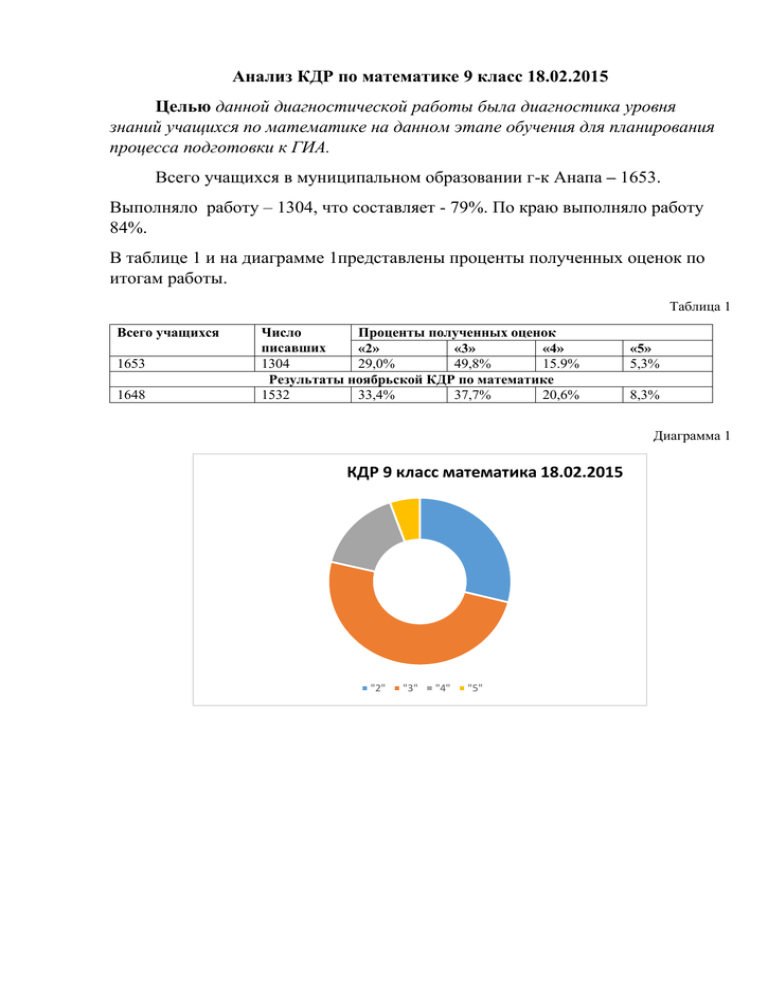
Анализ КДР по математике 9 класс 18.02.2015
Целью данной диагностической работы была диагностика уровня
знаний учащихся по математике на данном этапе обучения для планирования
процесса подготовки к ГИА.
Всего учащихся в муниципальном образовании г-к Анапа – 1653.
Выполняло работу – 1304, что составляет - 79%. По краю выполняло работу
84%.
В таблице 1 и на диаграмме 1представлены проценты полученных оценок по
итогам работы.
Таблица 1
Всего учащихся
1653
1648
Число
Проценты полученных оценок
писавших
«2»
«3»
«4»
1304
29,0%
49,8%
15.9%
Результаты ноябрьской КДР по математике
1532
33,4%
37,7%
20,6%
«5»
5,3%
8,3%
Диаграмма 1
КДР 9 класс математика 18.02.2015
"2"
"3"
"4"
"5"
Диаграмма 2
Сравнительное количество оценок ноябрь ,
февраль
60.00%
49.80%
50.00%
40.00%
30.00%
37.70%
33.40%
29%
20.60%
15.90%
20.00%
8.30%
5.30%
10.00%
0.00%
"2"
"3"
ноябрь
"4"
"5"
февраль
Процент неудовлетворительных оценок по образовательным учреждениям
колеблется от 62,5% до 3,1%.
Процент отличных оценок: от 11,1% до 2,1 %.
Средний балл по краю составил 5,63%, по муниципалитету - 6,16.
Наивысший балл по краю - 6,61, по муниципалитету – 7,56.
Наименьший средний балл по краю - 4,93, по муниципалитету – 4,55.
Работа состояла из 10 заданий, 9 из которых – задания базового уровня
сложности по модулям «Алгебра», «Геометрия» и одно повышенного уровня
сложности по модулю «Геометрия». Задания проверяли знания учащихся,
полученные по математике за 7-8 класс и 1 полугодие 9 класса.
Средний процент выполнения заданий в ноябре и феврале представлен на
диаграмме 2.
Диаграмма 2
Процент учащихся верно выполнивших задания
90.00%
80.00%
70.00%
60.00%
50.00%
40.00%
30.00%
20.00%
10.00%
0.00%
№1
№2
№3
№4
ноябрь
№5
№6
февраль
№7
№ 8
№9
№ 10
(1б)
№
10(2б)
край-февраль
Из диаграммы видно, что результат выполнения всех заданий базового уровня
сложности составил от 15,6% до 76,2%. Это достаточно невысокий результат.
Анализ выполнения каждого задания
данной диагностической работы по модулям.
Модуль «Алгебра»
Задание № 1 (с кратким ответом), проверяло умение учащихся выполнять
арифметические действия с целыми числами.
Приведем пример задания: «Найдите значение выражения 28:( 4) - 12 . (-2) ».
Уровень выполнения невысок. Выполнили 74,7 % (в крае -78,1%) писавших
девятиклассников.
Задание № 2 (с выбором ответа) проверяло умение учащихся применять
формулы сокращенного умножения при сокращении алгебраических дробей.
Пример задания: «Упростите выражение
70,8 % (в крае -79,1%).
𝑎2 −4𝑎𝑐+4𝑐 2
2𝑎−4𝑐
». Это задание выполнило
Задание № 3 (с кратким ответом), проверяло умение учащихся решать
квадратные (полные и неполные) уравнения.
«Решите уравнение 6𝑥 2 = 12𝑥 ».
Справились с этим заданием 66,7% (в крае -68,4%). На ГИА в 2014 г. задание
похожего типа выполнили 83% выпускников.
Задание № 4 (с выбором ответа) проверяло умение учащихся упрощать
выражения со степенями.
Уровень выполнения составил 66,6 % (в крае -71,1%).
Задание № 5 (на соотнесение), проверявшее умение учащихся правильно
соотносить график функции и формулой, задающей функцию, или соотнесение
графика квадратичной (линейной) функции с коэффициентами, выполнили
63,5% учащихся (в крае - 68,2%).
Задание № 6 (с выбором ответа) проверяло умение учащихся решать линейные
неравенства. С заданием справились 59,3% девятиклассников (в крае - 62,2%).
На ГИА 2014 г. с похожим заданием справилось 90% выпускников.
Количество учащихся набравших за задания 1- 6 до 2-х баллов 22%.
Подводя итог выполнения учащимися базовых заданий модуля «Алгебра»
хочется отметить, что все задания были выполнены на уровне 59,3% - 74,7%.
Это очень тревожный результат. Ошибки в заданиях могут быть связаны не
только с непониманием самого вопроса, но и с ошибками в вычислениях.
Модуль «Геометрия»
Задание № 7 (с кратким ответом), проверяло умение учащихся применять
теорему косинусов или теорему синусов. Верно выполнили 8,5% (в крае –
21,1%).
Пример задания: «В треугольнике ABC , найдите длину стороны BC , если AC
= 10 , AB=√39 , а cos ВАС =−
3√39
».
78
Очень низкий результат. 90% учащихся либо не знают формулы, либо
ошиблись в вычислениях.
Задание № 8 (с кратким ответом), проверяло умение учащихся вычислять
площадь фигуры на клетчатой бумаге.
Например: Найдите площадь фигуры, изображенной на рисунке.
Это задание выполнили 40,8% ( край -50,9%). На ГИА 2014 г. с этим заданием
справились 68%
Задание № 9 (с кратким ответом), проверяло умение учащихся анализировать
утверждения по геометрии и выбирать из них верные.
Одно из заданий: Укажите номера верных утверждений. 1) В равнобедренной
трапеции противоположные углы равны. 2) Около любого треугольника можно
описать окружность. 3) Сумма двух острых углов всегда больше прямого угла.
4) Две различные прямые, перпендикулярные к третьей, не пересекаются.
Уровень выполнения составил 42,6% (край – 43,3). ГИА 2014 -81%.
Подводя итог выполнения учащимися заданий базового уровня модуля
«Геометрия», хочется отметить, что задания были выполнены на разных
уровнях. Ошибки , вероятно, связаны с неумением внимательно читать текст
задания, незнанием формул, а также проблемы с вычислительными навыками.
Задание № 10 проверяло умение учащихся «решать прямоугольный
треугольник. Пример: «Дан прямоугольный треугольник АВС. Из вершины
прямого угла на гипотенузу опущена медиана СН. Найдите длину гипотенузы
АВ, если АС = 7, а угол АНС равен 1200» .
Результаты следующие: 2,1 % получили за выполнение задания 1 балл, 7,2 %
учащихся получили 2 балла. По краю соответственно - 4,2% и 8,1%. Немногие
учащиеся смогли сориентироваться в достаточно несложном задании.
Количество учащихся, набравших за задания 7-10 менее двух баллов за
выполнение заданий из модуля «Геометрия» составило 71% (58,7% в крае).
Очень тревожный результат.
Рекомендации учителям:
− продолжить работу по закреплению вычислительных навыков учащихся;
− обратить внимание на повторение тем: «Графики элементарных функций»,
«Квадратные уравнения», «Линейные неравенства», так как по ним уровень
выполнения в среднем по краю ниже 70 %;
− обратить внимание на преподавание геометрии;
− обратить внимание на развитие у учащихся умения внимательно читать и
анализировать текст задания, переводить его на математический язык и
составлять математическую модель;
− выделить «проблемные» 3-4 темы в каждом конкретном классе и работать
над ликвидацией пробелов в знаниях и умениях учащихся по этим темам, после
чего можно постепенно подключать другие темы;
− со слабыми учащимися в первую очередь закрепить достигнутые успехи,
предоставляя им возможность на уроке выполнять 15 – 20 минутную
самостоятельную работу, в которую включены задания на отрабатываемую
тему;
− с сильными учащимися проводить разбор методов решения задач
повышенного уровня сложности, проверяя усвоение этих методов на
самостоятельных работах и дополнительных занятиях.
Апрельская КДР по математике будет содержать задания аналогичные
базовой части ОГЭ. Длительность 90 минут.