1 Схемы для уравнения переноса
реклама

1
Разностные схемы для уравнений гиперболического типа
1 Схемы для уравнения переноса
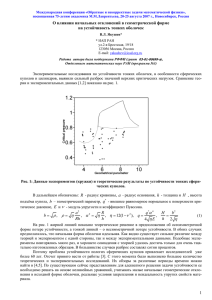
Рис. 1
Для простейшего уравнения переноса
ut u x 0, const , 0 ,
все
множество
явных
линейных
схем
на
5-точечном
(см. рис. 1; dx dt — характеристика уравнения (1)) с узлами:
(m,n+1), (m–2,n), (m–1,n), (m,n), (m+1,n)
имеет вид:
сеточном
(1)
шаблоне
(2)
umn1 um ,
n
(3)
,
0
0
с 4-мя неопределенными коэффициентами (рис. 1): 2
, 1
, 00 , 10 . Из них, после
удовлетворения условий аппроксимации первого порядка
0 1 0, 1 ( ) 0,
(4)
,
,
0
— число Куранта) два коэффициента, например, 2
, 00
( / h
остаются
свободными, а два другие, например, , выражаются через эти свободные
0
коэффициенты. Принимая 2
, 00 за координаты линейного пространства с евклидовой
метрикой, в котором каждой точке соответствует некоторая схема 1-го порядка аппроксимации,
можно найти все множество устойчивых схем (при 0< <1 — область B1 , B2 , C, B3 , B4 , A3 , A4 , A0
(голубой цвет) на рис. 2), все монотонные схемы (положительные по Фридрихсу, то есть такие,
у которых все коэффициенты
неотрицательны, (при 0< <1 — зеленый четырехугольник
0
1
0
1
A0 , A1 , A3 , A4 на рис. 2), однопараметрическое семейство схем 2-го порядка аппроксимации
2 2 ( ) 2 0,
(5)
,
(отрезок B1 B4 на рис. 2 — устойчивые при 0< <1 схемы с порядком аппроксимации выше
первого), единственную на этом шаблоне схему 3-го порядка аппроксимации:
3 3 ( )3 0,
(6)
,
(при 0< <1 точка C на рис. 2)
На основе этих множеств можно строить оптимальные в том или ином смысле схемы,
например, "наиболее точную из монотонных схем" — точка A1 , "наименее осциллирующую на
разрывных решениях схему 2-го порядка аппроксимации" — точка B2 на рис. 2, гибридные
схемы (схемы с переменным порядком аппроксимации — первым вблизи разрывов и вторым
2
или третьим в области гладкого повеления решения) и т.д. Красный треугольник A1B2C на рис. 2
есть множество наиболее удачных схем (по соотношению точности и устойчивости).
Рис. 2
Аналогичные рис. 2 построения могут быть выполнены при 1< <2 и при –1< <0. В
частности, при <0 аналогичные рис. 2 разностные схемы получаются заменой на – и
коэффициентов на . Например, если для т. A1 (при >0) имеем:
02 20 10 0 , 01 , 00 1 , то для аналогичной точки при <0 02 20 01 0 ,
10 , 00 1 .
Для построения гибридных схем каждый из коэффициентов вектора { 02 , 00 , 20 }
можно задавать в виде линейной комбинации двух опорных схем – монотонной схемы 1-го
порядка 1 – одной из точек многогранника A0 , A1 , A3 , A4 (при 0< <1) – и немонотонной
схемы 2-го или 3-го порядка аппроксимации 2 – одной из точек отрезка B1 B4 :
( , g ) g1 ( ) (1 g ) 2 ( )
(7)
При этом g(u) выбирается в зависимости от поведения решения так, чтобы вблизи разрывов g=1,
а в области гладкого поведения g=0, например, “по Ван-Лиру”:
g (umn 1 , umn , umn 1 ) (1 ( 2q 1)(| 2q 1 | 10 6 ) (1/ k 1) ) / 2 ,
q | dp dm | /( dp dm 10 6 ) ,
dp || umn 1 | | umn || , dm || umn | | umn 1 || , k=2÷10.
(8)
2 Схемы для линейных систем уравнений гиперболического типа
Система может быть задана в следующей (недивергентной) форме
Vt AVx 0 , V {v1 ,..., vI } , A {aij } 1 , aij const , i,j=1,…,I,
(10)
где {i } – диагональная матрица из собственных значений i , i=1,...,I матрицы A,
определяемых из характеристического уравнения PI ( ) Det ( A E ) 0 , E – единичная
матрица, {i } – неособенная матрица, строками которой являются линейно-независимые
левые собственные векторы матрицы A i { i1 ,..., iI } , для каждого i , с точностью до длины
определяемые из линейных однородных систем уравнений i ( A i E ) 0 ).
Тогда аналоги разностных схем (3), сохраняющие все описанные выше свойства (порядок
аппроксимации, устойчивость, монотонность и т.д.), имеют вид:
Vmn 1
,
1
n
A Vm ,
(11)
где
A
{
i }
– диагональные матрицы, элементы которых
3
i ) , i i / h
i (
0
соответствуют рассмотренным выше построениям (т. A0 , A1 A4 , B1 B6 , C при i >0,
2 =0
на рис.2). Для разных i и значений i набор коэффициентов i
может соответствовать
разным точкам.
Для квазилинейной системы гиперболического типа в дивергентной форме
Wt (V ) Fx (V ) 0 , W {w1 ,..., wI } , F { f1 ,..., f I } , Det (W / V ) 0 ,
которой соответствует недивергентная форма типа (10):
Wt R(W )Wx 0
(12)
(13)
R F / W (F / V )(V / W ) (F / V )(W / V ) 1 1
или
(14)
Vt A(V )Vx 0 , A (W / V ) 1 (F / V ) = 1 ,
на том же сеточном шаблоне, что и на рис.1, используя интегро-интерполяционный метод,
можно построить семейство консервативных разностных схем с тем же числом свободных
параметров, что и в случае линейной системы (10) (трехпараметрическое – 1-го порядка
аппроксимации, двухпараметрическое – 2-го и т.д.). Например, можно построить семейство
двухшаговых схем с неустойчивым предиктором
~
Wmn 1 = Wmn - ( Fmn1 - Fmn1 )/(2h),
(15)
и корректором
~
~
~
~
~
Wmn 1 = Wmn 1 +( 1C ) m 1 / 2 ( Wmn11 - Wmn 1 )-( 1C ) m 1 / 2 ( Wmn 1 - Wmn11 )+ ( 1 B ) m 1 / 2 ( Wmn1 - Wmn ) –
~
~
– ( 1 B ) m 1 / 2 ( Wmn - Wmn1 )+( 1 D ) m 1 / 2 (( Wmn11 + Wmn 1 ) – ( Wmn1 + Wmn )) –
(16)
~
~
– ( 1 D ) m 1 / 2 (( Wmn 1 + Wmn11 )- ( Wmn + Wmn1 )),
где B diag{bi } , C diag{ci } , D diag{d i } - диагональные матрицы.
Если в (12) положить W=V, F=AV и сопоставить (15),(16) с (11), то можно установить взаимно
однозначную связь коэффициентов bi , ci , d i из (16) с 02i , 00i , 20i из (11), а значит и из (3):
bi 0.5(1 00i (20i (2 i ) 02i (2 i )) / i )
(17)
ci ( 02i 20i ) / i , di ( 02i 20i ) / i
и, тем самым, получить консервативные аналоги разностных схем, соответствующих точкам A0
(схема Лакса), A1 - A1' (аналог схемы Куранта-Изаксона-Риса), B3 - B3' (аналог схем ЛаксаВендроффа и Маккормака) и т.д., если соответствующим образом выбирать коэффициенты
02i , 00i , 20i .
Пример системы уравнений гиперболического типа – одномерные уравнения газодинамики:
u
2
Переменные V u ; для дивергентной формы системы W (V ) u ; F (V ) u p ,
E
u( E p )
2
u
где – плотность, u – скорость, – удельная внутренняя энергия, E
- удельная
2
полная энергия, p ( 1) – давление, 1.4 - показатель адиабаты воздуха. Для этой
системы хорошо исследована «задача о распаде разрыва» в области 0 t T , 0 x 1 с
VL {10,0,1}, 0 x 0.5
начальными условиями вида V (0, x )
и граничными условиями
VR {1,0,1}, 0.5 x 1
V (t , x 0) / t 0, V (t , x 1) / t 0 .
4
3 Примеры разностных схем
1 Схемы 1-го порядка
1.1 наиболее точная при значениях числа Куранта 0< <1 монотонной схеме (т. А 1 :
00 1 , 02 0 )
1.2 схема Лакса, для которой 00 02 0 (т. A0 )
1.3 00 =1– /2, 02 = /2 (т. A3 )
1.4 00 =0, 02 =( +1)/3 (т. A4 )
2 Схемы 2-го порядка
2.1 наименее осциллирующая на разрывных решениях схема ( 02 =3 ( –1)/10 — т. B2 )
2.2 схема Лакса-Вендроффа, у которой 02 =0 (т. B3 ),
2.3 схема Бима-Уорминга, у которой 02 = ( –1)/2 (т. B5 )
2.4 схема Фромма, у которой 02 = ( –1)/4 (т. B6 )
2.5 02 =( 2 –1)/4 (т. B 1 ; граница множества устойчивых схем)
2.6 02 =( 2 –1)/4 и 02 = 2 /4 (т. B 4 ; граница множества устойчивых схем)
3 Схема 3-го порядка аппроксимации (т. C: a 02 = ( 2 –1)/6; коэффициент a 00 =3a 02 +1– 2
вычисляется в соответствии с (5)).