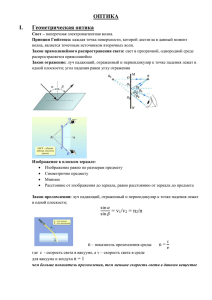
I φ
реклама

ФИЗИКА. РАЗДЕЛ “ОПТИКА”. Лабораторные работы 1 Составители: Дроздов С.А. Гадзаова О.Э. Соловьёв П.В. Под общей редакцией Л.И. Уруцкоева, доктора физико-математических наук, профессора. 2 Работа № 1 ОПРЕДЕЛЕНИЕ ГЛАВНЫХ ФОКУСНЫХ РАССТОЯНИЙ СОБИРАЮЩЕЙ И РАССЕИВАЮЩЕЙ ЛИНЗ Цель работы Изучить законы геометрической оптики применительно к тонким собирающим и рассеивающим линзам. Приборы и принадлежности Оптическая скамья с сантиметровой шкалой, рейтеры-держатели с линзами, электрическая лампа, предмет и экран. Теоретическое обоснование То, что мы называем светом, представляет собой электромагнитные волны, основные свойства которых, определяются решением уравнений Максвелла. Однако простейшие оптические явления, например возникновения теней и получение изображений в оптических приборах, могут быть поняты в рамках так называемой геометрической оптики. Раздел оптики, в котором при изучении распространения света пренебрегают длиной электромагнитных волн, называют геометрической оптикой. Распространение света в геометрической оптике описывают с помощью световых лучей. Световой луч – это линия, вдоль которой распространяется световая энергия. В основе формального построения хода световых лучей в рамках геометрической оптики, лежит четыре закона, установленных опытным путем: 1) закон прямолинейного распространения света; 2) закон независимости световых пучков; 3) закон отражения; 4) закон преломления света (закон Снеллиуса). Объекты, от которых исходят световые лучи, называют источниками. В рамках геометрической оптики часто используют такую идеализацию как точечный источник. Точечный источник – это точка пространства, из которой исходит бесконечно много световых лучей. Реальный источник можно считать точечным, если его размеры малы по сравнению с расстояниями между элементами оптической схемы. Источник конечных размеров можно представить как совокупность точечных источников. Поэтому наряду с понятием светового луча для описания распространения света используют понятие светового пучка. Световой пучок представляет собой совокупность бесконечного числа световых лучей, идущих от какоголибо источника. 3 Световые пучки, проходя через какую-либо оптическую систему, могут изменять характер своего распространения. Может получиться так, что для точечного источника все те лучи светового пучка, которые прошли через оптическую систему, снова будут пересекаться в некоторой точке. В этом случае говорят о том, что оптическая система формирует действительное изображение, а саму точку пересечения лучей называют изображением точечного источника. Возможен вариант, когда после выхода из системы будут пересекаться не сами лучи, а их продолжения. В этом случае принято говорить о формировании мнимого изображения. Точки пространства, в которых расположены точечный источник и его изображение, называются сопряженными точками. Если для пары сопряженных точек поменять местами положение источника и его изображения и изменить направление распространения лучей на противоположное, то лучи через систему будут распространяться по тем же линиям, по которым они распространялись до указанной замены. Это свойство называется обратимостью световых лучей. Одной из основных задач геометрической оптики является расчёт хода лучей в оптических приборах, предназначенных для получения изображений. Простейшим элементом таких приборов является линза, изучению которой и посвящена настоящая работа. Линза представляет собой прозрачное тело, ограниченное с двух сторон сферическими поверхностями, преломляющими световые лучи, способное формировать оптические изображения предметов. В частном случае одна из поверхностей линзы может быть плоскостью, которую можно рассматривать как сферическую поверхность бесконечно большого радиуса. На рисунке 1 представлены линзы, образованные двумя пересекающимися сферическими поверхностями (а) и непересекающимися поверхностями (б). Мы будем рассматривать тонкие линзы, в которых расстояние О1О2 пренебрежимо мало по сравнению с О1С1 или О2С2 и расстоянием от предмета до линзы. Точки О1 и О2 в тонкой линзе расположены столь близко друг к другу, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают точкой О. а) б) Рис.1. К определению линзы. 4 Всякая прямая, проходящая через оптический центр линзы, называется оптической осью линзы. Та из осей, которая проходит через центры обеих сферических поверхностей линзы, называется главной оптической осью (прямая mn); остальные – побочными осями. Плоскость, проходящая через главный оптический центр линзы О перпендикулярно ее главной оптической оси, называется главной плоскостью линзы. Луч, идущий по какой-либо из оптических осей, проходя через линзу, практически не меняет своего направления. Если на линзу падает световой луч не вдоль одной из оптических осей, а по какому-либо другому направлению, то он, испытав преломление сначала на первой ограничивающей линзу поверхности, потом на второй, отклонится от первоначального направления. По своим оптическим свойствам линзы делятся: на собирающие – преломлённый луч отклоняется в сторону главной оптической оси и рассеивающие – преломлённый луч отклоняется от главной оптической оси. Абсолютным коэффициентом преломления среды называется величина n, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости в среде: n = c/v . Если коэффициент преломления линзы nл больше, чем коэффициент преломления окружающей среды nср, то собирающими линзами будут двояковыпуклые (рис.2 а), плосковыпуклые (рис.2 б) и вогнутовыпуклые линзы (рис.2 в), т.е. линзы, утолщающиеся к середине (они называются выпуклыми). К рассеивающим линзам в этом случае принадлежат двояковогнутые (рис.3 а), плосковогнутые (рис.3 б) и выпукловогнутые (рис.3 в), т.е. линзы, становящиеся тоньше к середине (вогнутые). В том случае, если nл < nср, то приведённая выше классификация линз на собирающие и рассеивающие будет обратной. Рис. 2. Выпуклые линзы. Рис. 3. Вогнутые линзы. Лучи, падающие на собирающую линзу параллельно главной оптической оси, преломляются ею, собираясь в одной точке F, называемой действительным (главным) фокусом (рис.4). 5 Рис. 4. Фокус собирающей линзы. При построении изображений вместо линзы графически обозначают только её главную плоскость. Так на рисунках 4 ÷ 6 показано как будут преломляться оптические лучи в линзах разных типов. Плоскость, проходящая через фокус линзы F перпендикулярно ее главной оптической оси mn, называется фокальной плоскостью линзы. Расстояние от оптического центра линзы до фокуса f называется фокусным расстоянием. Фокусное расстояние тонкой линзы связано с радиусами кривизны и ограничивающих её сферических поверхностей соотношением 1 𝒇 = 𝒏л −𝒏ср 1 ( 𝒏ср 𝑅1 + 1 𝑅2 ) , (1) где 𝒏л – абсолютный коэффициент преломления материала линзы, 𝒏ср – абсолютный коэффициент преломления среды, радиусы кривизны считаются положительными для выпуклых поверхностей и отрицательными для вогнутых. Величину D = (n – 1)( 1 𝑅1 + 1 𝑅2 ), где n = n2/n1 – относительный показатель преломления, обратную фокусному расстоянию, называют оптической силой тонкой линзы; единица измерения – диоптрия. 1дп = 1м-1. У собирающей линзы f > 0, D > 0; у рассеивающей – f < 0, D < 0. Рассмотрим случай, когда на собирающую линзу падает произвольный луч (не параллельный главной оптической оси). Как узнать направление его хода после преломления? Для этого нужно построить с другой стороны линзы фокальную плоскость ab (рис.5) и провести через главный оптический центр линзы вспомогательный луч, параллельный лучу, заданному нам произвольно. Пусть вспомогательный луч пересечет фокальную плоскость ab в некоторой точке K . Тогда, поскольку произвольный и вспомогательный луч параллельны, через точку K пойдет произвольный луч после преломления в линзе. Точки пересечения всех лучей, падающих на линзу в виде параллельных пучков, будут располагаться в плоскости, перпендикулярной главной оптической оси и проходящей через главный фокус (фокальная плоскость). В зависимости от угла падения пучка, точка пересечения лучей, составляющих 6 пучок, будет лежать в фокальной плоскости на том или ином расстоянии от главной оптической оси. Рис.5. Параллельные лучи после преломления в собирающей линзе. Лучи, падающие на рассеивающую линзу параллельно главной оптической оси, после преломления в линзе идут расходящимся пучком. Продолжения этих лучей пересекаются в мнимом (главном) фокусе (рис.6). Рис.6. Мнимый фокус рассеивающей линзы. Если на рассеивающую линзу падает произвольный луч (рис.7), то для того, чтобы узнать направление его хода после преломления, нужно построить фокальную плоскость со стороны падающего луча, а затем провести вспомогательный луч параллельно падающему (через точку О). Пусть вспомогательный луч пересечет фокальную плоскость в точке К. Преломлённый луч пойдёт по прямой, проходящей через точку К и точку пересечения произвольного луча с плоскостью линзы. Рис.7. Параллельные лучи после преломления в рассеивающей линзе. 7 Построение изображения предмета в линзах. Каждая светящаяся точка источника является вершиной расходящегося пучка лучей. Такой пучок называется гомоцентрическим, буквально «имеющим общий центр». Если после отражения и преломления этот пучок превращается в пучок, сходящийся также в одну точку, то и последний является гомоцентрическим. Центр его называется изображением светящейся точки. При сохранении гомоцентричности каждая точка источника дает одну точку изображения. Такие изображения называются точечными или стигматическими. В основе всех построений лучевой оптики лежат законы преломления и отражения света. Рассмотрим еще один важный принцип, который строго соблюдается при явлениях преломления и отражения света – принцип взаимности, или обратимости световых лучей. В силу взаимной обратимости световых лучей изображение можно рассматривать как источник, а источник – как изображение. Поэтому при стигматическом изображении центры пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся. Соответственные лучи и пучки также называются сопряженными. Если известно фокусное расстояние тонкой линзы, то изображение предмета может быть получено путём простых геометрических построений. При этом нужно иметь в виду несколько общих правил: 1. Построение изображения проводится путём построения изображения каждой его точки. Как правило, строят изображение крайних точек предмета. 2. Для построения изображения любой точки предмета необходимо выбрать как минимум два луча, выходящие из этой точки, направления которых после преломления известны. Точка пересечения этих лучей или их продолжений после прохождения через линзу и будет служить изображением точки предмета. В качестве таких лучей берут (рис. 8,9): а) луч 1, проходящий через оптический центр линзы О, после выхода из линзы не меняет своего направления; б) луч 2, параллельный главной оптической оси, после прохождения через линзу пройдёт через её главный фокус – рис. 8, (или его продолжение – через мнимый, рис. 9); в) луч 3, проходящий через главный фокус линзы; после прохождения через линзу этот луч выйдет параллельно главной оптической оси. А - светящаяся точка, А' - ее изображение. 8 Рис. 8. Рис. 9. Формула тонкой линзы Из геометрии построений рис. 8,9 легко получить формулу тонкой линзы: 1 𝒇 = 1 1 a b . (2) Величины a, b, f могут быть как положительными, так и отрицательными. Если линза собирающая, то ее фокус действительный, и f > 0 (рис. 8). В случае рассеивающей линзы её фокус мнимый и f < 0 (рис. 9). Величина b положительная, если изображение действительное, и отрицательная в случае мнимого изображения. Наконец, a положительная величина, в случае действительной светящейся точки, и отрицательная, если источник мнимый (т.е. на линзу падает сходящийся пучок лучей, продолжения которых пересекаются в одной точке). Из (2) получим: f ab . ab (3) Измерив из опыта а и b и пользуясь формулой (3), можно рассчитать фокусное расстояние линзы. Описание установки и подготовка ее к работе Установку составляет оптическая скамья. Вдоль её станины на рейтерахдержателях могут перемещаться источник света, линзы, экран (рис. 10). Предметом для получения изображений на экране служит изображение стрелки, освещаемая электрической лампочкой. 9 Рис. 10. Измерительная установка. Перед началом измерений система должна быть центрирована, для чего нужно выставить все элементы схемы по высоте так, чтобы их центры лежали на одной горизонтальной прямой. Плоскость экрана и поверхности линз должны быть перпендикулярны оптической оси. Расположив линзу между осветителем и экраном, получите резкое изображение стрелки на экране. Перемещая линзу и экран, заметьте примерное расположение приборов при увеличенном, уменьшенном и равном предмету изображении. Если поместить непосредственно за линзой диафрагмы различной формы, то вид изображения не будет зависеть от формы диафрагмы. Объясните этот факт. Что меняется при замене одной диафрагмы другой? При данном положении линзы и источника резкость изображения на экране незначительно меняется при небольших смещениях экрана – существует так называемая глубина резкости. То же самое можно наблюдать, сдвигая незначительно источник при неподвижном экране и линзе. Убедитесь в этом на опыте. Если уменьшать размеры отверстия диафрагмы, расположенной рядом с линзой, то глубина резкости увеличивается при уменьшении отверстия диафрагмы. Этот эффект широко применяется в фотографии. Объясните его, используя рис.11. В плоскости Σ получается точечное изображение источника Р. В плоскости Σ’ и Σ” – изображение в виде кружков рассеяния1. ______________________ Опытами установлено, что на расстоянии наилучшего зрения (25 см) кружки рассеяния менее 0,1 мм в диаметре воспринимаются глазом как точки. 1 10 Рис. 11. Изменение глубины резкости изображения при изменении отверстия диафрагмы оптической системы. Определение главного фокусного расстояния собирающей линзы Определите главное фокусное расстояние собирающей линзы следующими двумя способами и сравните между собой результаты. Какой способ вы считаете более точным? Измерения обязательно проведите не менее пяти раз, меняя расстояние между элементами оптической схемы. Оцените ошибку измерений для каждого метода. Попытайтесь указать причины расхождения результатов, полученных разными методами. Способ 1. Получая резкие изображения сетки и измеряя a и b, находим f. Проведите не менее 5 измерений при разных a и b, найдите среднее f и его среднеквадратичное отклонение. То же самое повторить для другого способа. Для измерения фокусного расстояния: 1. Установите и закрепите на левом краю скамьи источник света. На другом конце скамьи установите экран. 2. Постепенно отодвигая линзу от источника, добейтесь получения чёткого изображения предмета – стрелки. 3. Измерьте а – расстояние от предмета до линзы и b – расстояние от линзы до экрана. Занесите данные в таблицу 1. 4. Сместите экран вдоль скамьи. Перемещением линзы снова добейтесь получения чёткого изображения стрелки на экране. Измерьте и запишите в таблицу новые значения а и b. 5. Определите относительную и абсолютную погрешности измерений и занесите их в таблицу: Е1 = ∆𝒇 𝒇𝒄𝒑 = ∆𝒂 𝒂 + ∆𝒃 𝒃 + ∆𝒂+ ∆𝒃 𝒂+𝒃 ∆𝒇 = Е1𝒇𝒄𝒑 . , 11 Таблица 1. N 1 2 … 5 Cp. а (см) b (см) f (см) E1 ∆f (см) fcp = % ± Способ 2 (Бесселя). Это один из самых точных методов измерения фокусного расстояния линзы. Если расстояние от предмета до изображения более 4f , то всегда найдутся два таких положения линзы, при которых на экране получится отчетливое изображение предмета (рис. 12). При этом положения линзы будут симметрично расположены относительно середины отрезка L, а расстояние от источника до линзы в первом случае будет равно расстоянию от линзы до экрана во втором. Обозначим через d смещение линзы между двумя положениями, при которых на экране наблюдается чёткое изображение. Для первого положения линзы 12 Рис. 12. Два положения собирающей линзы, при которых на экране получается отчётливое изображение предмета (увеличенное и уменьшенное). Определить фокусное расстояние f собирающей линзы по способу Бесселя. Для этого: 1. С помощью собирающей линзы получите чёткое увеличенное изображение предмета на экране аналогично тому, как это делалось в предыдущем способе. 2. Измерьте расстояние L и запишите его в таблицу 2. 3. Отметьте на оптической скамье положение линзы. Перемещая линзу, получите на экране уменьшенное изображение предмета. Измерьте перемещение линзы и занесите его значение в таблицу. 4. Изменяя расстояние между предметом и экраном, заполните остальные строки столбцов L и d. 5. По формуле (4) вычислите для каждого положения линзы фокусное расстояние и заполните соответствующий столбец таблицы. 6. Определите относительную и абсолютную погрешности измерений и занесите их в таблицу: Е2 = ∆𝒇 𝒇𝒄𝒑 = ∆L/L + 2(L∆L+ d∆d)/(𝑳𝟐 − 𝒅𝟐 ) . ∆𝒇 = Е2𝒇𝒄𝒑 . Таблица 2. N 1 2 … 5 Cp. L (см) d (см) 13 f (см) E2 ∆f (см) fcp = % ± Определение фокусного расстояния рассеивающей линзы Способ основан на измерении расстояний от предмета и его изображения до линзы. Так как с помощью только одной рассеивающей линзы невозможно получить действительное изображение предмета, то в этом случае используют также собирающую линзу. На рис. 13 показана схема определения фокусного расстояния рассеивающей линзы. Сначала с помощью собирающей линзы (O1) получают на экране (положение 1) отчётливое изображение P1′ предмета P . Затем ставят рассеивающую линзу (O2) близко к экрану. Изображение предмета становится нечетким. Для получения четкого изображения P2′ экран передвигают от рассеивающей линзы в положение 2. В силу принципа обратимости световых лучей можно мысленно рассмотреть лучи, распространяющиеся из P2′ в обратную сторону. Тогда точка P1′ будет мнимым изображением точки P2′ после прохождения лучей через рассеивающую линзу O2 . Расчёт фокусного расстояния проводится по формуле (3) (с учётом того, что f и b имеют отрицательные знаки). Для определения фокусного расстояния рассеивающей линзы: Рис. 13. Оптическая схема для определения фокусного расстояния рассеивающей (отрицательной) линзы. 1. Установите источник света и экран на расстоянии, немного превышающем учетверенное фокусное расстояние собирающей линзы (воспользуйтесь результатами предыдущего упражнения). 2. Поставьте между ними собирающую линзу и получите четкое уменьшенное изображение предмета. 3. Установите между собирающей линзой и экраном рассеивающую линзу (рис. 13). Занесите в таблицу 3 отсчёты против указателя рассеивающей линзы и экрана (положение экрана 1). Разница между этими отсчётами будет равна b (со знаком минус) 4. Отодвигая экран, добейтесь получения чёткого изображения предмета (положение экрана 2 – занесите его в таблицу). 14 5. Повторите пп. 3,4 для двух других положений рассеивающей линзы, заполнив таким образом столбцы а и b таблицы 3. 6. По формуле (3) вычислите для каждого положения линз фокусное расстояние и заполните соответствующий столбец таблицы. 7. Определите относительную и абсолютную погрешности измерений и занесите их в таблицу: Е3 = ∆𝒇 𝒇𝒄𝒑 = ∆𝒂 𝒂 + ∆𝒃 𝒃 + ∆𝒂+ ∆𝒃 𝒂−𝒃 ∆𝒇 = Е3𝒇𝒄𝒑 . , Таблица 3. N 1 2 3 Cp. а (см) b (см) f (см) E3 ∆f (см) fcp = % ± Контрольные вопросы и задания 1. Что такое изображение? Какое изображение называется действительным, а какое мнимым? 3. Выведите формулу для тонкой линзы. Какая линза называется собирающей, а какая рассеивающей? 4. Постройте изображение в системе линз (по усмотрению преподавателя). 5. Как из формулы линзы получить формулу для определения фокусного расстояния по способу Бесселя? 6. Теоретически определите фокусное расстояние используемой Вами собирающей линзы. (Измерьте толщину и диаметр линзы. Из геометрических соображений вычислите по этим данным радиусы кривизны. Показатель преломления стекла n = 1,5). Литература 1. Трофимова Т.И. Курс физики. М. Академия. 2008. Гл. 21, § 165, 166. 2. Савельев И.В. Курс общей физики. Кн. 4. СПб. Лань, 2008. Гл. 3, § 3.6 – 3.8. 15 Работа № 2 ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ ПО ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЕ КОЛЕЦ НЬЮТОНА. Цель работы Изучение явления интерференции света; наблюдение колец Ньютона; определение радиуса кривизны плоско-выпуклой линзы с помощью интерференционной картины колец Ньютона. Приборы и принадлежности Плоскопараллельная стеклянная пластинка с линзой (в оправе), микроскоп МБР-1 с осветителем, понижающий трансформатор 220/8 В, красный светофильтр. Теоретическое обоснование Две волны называются когерентными, если они колеблются с одинаковой частотой и с, не изменяющейся в течение длительного времени, разностью фаз. При наложении когерентных волн возникает их взаимное усиление в одних точках пространства и взаимное ослабление – в других. Это явление называется интерференцией. Для осуществления интерференции световых волн, помимо когерентности, необходимо, либо, чтобы совпали плоскости поляризации этих волн, либо чтобы эти волны были совсем не поляризованы (так называемый естественный свет). Световые волны от двух идентичных источников света всегда некогерентны, так как начальные фазы световых волн, излучаемых различными атомами, хаотически изменяются во времени. Поэтому для осуществления интерференции света необходимо пользоваться только одним источником, разделяя каким-либо способом излучаемый им свет на два пучка, а затем сводя эти пучка вместе. Результат интерференции зависит от оптической разности хода Δ интерферирующих пучков света и от длина волны λ в вакууме. Условие максимума освещённости в интерференционной картине: = ±2k∙λ/2 = ±k∙λ , k = 0, 1, 2... (1) Максимальное взаимное ослабление пучков света наблюдается при: = ±(2k + 1)∙λ/2 , k = 0, 1, 2... (2) Оптическая длина пути равна произведению геометрической длины пути света в данной среде на ее абсолютный показатель преломления n. Поэтому для световых волн, распространяющихся в вакууме n = 1или в 16 воздухе (n ≈1), оптическая разность хода Δ совпадает с геометрической разностью хода δ. Интерференция в тонких прозрачных пленках возникает в результате наложения волн, отраженных от верхней и нижней поверхностей пленки. Классическим примером такого рода интерференции являются кольца Ньютона. Этот случай наблюдается, когда выпуклая поверхность линзы (коэффициент преломления n1) малой кривизны соприкасается в некоторой точке с плоской стеклянной пластинкой (коэффициент преломления n3). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный клинообразный зазор между пластиной и линзой (коэффициент преломления n2) (рис.1). Будем считать, что n1 > n2 < n3. Наблюдение ведётся в отражённом свете. n1 n2 n3 Рис.1 Рассчитаем размеры колец Ньютона. Пусть сверху на плоскую поверхность линзы падает монохроматический параллельный пучок лучей. Луч 1 испытывает преломление на выпуклой поверхности линзы (граница раздела I) и отражается от поверхности пластинки (граница раздела II). Затем он снова преломляется на границе I . Луч 2 испытывает только отражение от границы I (см. рис. 1). Интерференционная картина в отраженном свете будет наблюдаться на выпуклой поверхности линзы (граница раздела I) за счет интерференции лучей 1 и 2. При вычислении разности хода можно пренебречь небольшими наклонами лучей, проходящих в тонком воздушном зазоре – точки А, С и D сливаются в одну точку как показано на рисунке 2. Геометрическая разность хода между интерферирующими лучами равна, очевидно, 2h, где h – толщина воздушного зазора в данном месте. 17 Выразим зависимость h от расстояния r до радиуса, проходящего через точку соприкосновения линзы и пластинки (ED на рис. 2). Из KDE (рис.2) имеем r2 = R2 – (R – h)2 = 2Rh –h2 , где R – радиус кривизны выпуклой поверхности линзы. Принимая во внимание, что 2R » h, получим h = r2/2R . (3) При вычислении полной разности хода нужно учесть изменение фазы световой волны при отражении от границ стекло – воздух и воздух – стекло. Как известно, для светового (электрического) вектора отражение от оптически более плотной среды происходит с изменением Рис.2 фазы на . Свет, отражённый от границы стекло – воздух, по сравнению со светом, отражённым от границы воздух – стекло, приобретает, таким образом, дополнительный фазовый сдвиг на , что соответствует разности хода /2. Полная разность хода равна = 2h + /2 = r2/R + /2 . (4) Интерференция наблюдается при условии неизменной оптической разности хода. В данной системе постоянная по величине разность хода располагается по окружностям (h неизменно по окружностям). Поэтому интерференционная картина имеет форму концентрических темных и светлых колец с центром в точке касания линзы и пластины (полосы равной толщины). Известно, что полосы равной толщины для точечного источника света не имеют области локализации: их можно наблюдать в любом месте пространства, где пересекаются лучи, отражённые от двух поверхностей. Для протяжённого источника полосы равной толщины локализованы на поверхности клина (в нашем случае на поверхности воздушной прослойки). Это означает, что при освещении системы не вполне параллельным пучком света (что практически всегда имеет место) интерференционные полосы оказываются наиболее чёткими при фокусировке на верхнюю поверхность воздушного клина. Приравнивая полную разность хода (4) и разность хода из условия максимального взаимного ослабления лучей (2), получим для радиусов rk тёмных колец rk2 = k∙ λ∙R . (5) Вследствие упругой деформации стекла и возможного попадания пыли в точку контакта между линзой и пластиной невозможно добиться 18 идеального соприкосновения линзы с плоскопараллельной пластиной, поэтому результат будет более правильным, если вычислять радиус кривизны линзы по разности квадратов радиусов двух темных колец rm и rn . Тогда окончательная расчетная формула примет вид R = (rm2 – rn2 )/(m – n) λ. (6) Измеряя радиусы тёмных колец, с помощью (6) и зная λ, можно рассчитать искомый радиус кривизны линзы. Описание установки и метода измерений Для наблюдения в отражённом свете колец Ньютона и измерения расстояний между ними используется микроскоп. В микроскопе выделяют две системы: оптическую и механическую (рис.3). К оптической системе относят объективы, окуляры и осветительную систему (конденсор с диафрагмой и светофильтром, зеркало или электроосветитель). Рис. 3. Устройство микроскопов: А - БИОЛАМ; Б - МБС-1. 1 - окуляр, 2 - тубус, 3 - тубусодержатель, 4 - винт грубой наводки, 5 микрометрический винт, 6 - подставка, 7 - зеркало, 8 - конденсор, ирисовая диафрагма и светофильтр, 9 - предметный столик, 10 - объектив, 11 - стойка, 12 - оптическая головка, 13 - рукоятка переключения увеличения, 14 - бинокулярная насадка. Объектив - определяет полезное увеличение объекта. Объектив состоит из нескольких линз. Увеличение объектива обозначено на нем цифрами. В учебных целях используют обычно объективы х8 и х40. 19 Окуляр состоит из 2-3 линз. Увеличение окуляров обозначено на них цифрами: х7, х10, х15. Окуляры не выявляют новых деталей строения и в этом отношении их увеличение бесполезно. Для определения общего увеличения микроскопа следует умножить увеличение объектива на увеличение окуляра. Осветительное устройство состоит из зеркала или электроосветителя, конденсора с ирисовой диафрагмой и светофильтром, расположенных под предметным столиком. Они предназначены для освещения объекта пучком света. Механическая система микроскопа состоит из подставки, коробки с микрометрическим механизмом и микрометрическим винтом, тубусодержателя, винта грубой наводки, кронштейна конденсора, винта перемещения конденсора, револьвера, предметного столика. Оптическая система «пластинка – собирающая линза» устанавливается на предметный столик 9 микроскопа. Источником света служит осветитель (монохроматического – с красным светофильтром). Лампочка осветителя питается от понижающего трансформатора, включаемого в сеть. Понижающий трансформатор имеет выключатель питания и позволяет изменять силу света. Для поиска колец Ньютона необходимо сфокусировать микроскоп на поверхности стеклянной пластинки. На поверхности пластинки для этого в одном из углов нанесены риски. Перемещая оптическую систему «пластинка – собирающая линза» в горизонтальной плоскости можно добиться появления в поле зрения окуляра колец. Фокусировка колец (их установка на резкость) производится вращением винта грубой наводки 4 и микровинта 5. Примечание. При помощи микрометрического винта можно добиться хорошего изображения объекта. На коробке микрометрического механизма имеются две риски, а на микрометрическом винте – точка, которая должна все время находиться между рисками. Если она выходит за их пределы, ее необходимо возвратить в нормальное положение. При несоблюдении этого правила, микрометрический винт может перестать действовать. С помощью окулярной шкалы можно измерять расстояние между кольцами. Измерение радиуса кривизны линзы. 1. Добившись с помощью описанной выше методики появления колец Ньютона в поле зрения окуляра, совмещают его с пересечением визирных линий. Освещение производится монохроматическим светом с использованием красного светофильтра. 2. Повернув окуляр так, чтобы его шкала расположилась горизонтально, делают по ней отсчёты, соответствующие сначала левым концам диаметров колец Nлев.(всех наблюдаемых колец), затем – соответствующие их правым концам Nправ.. Отсчёты Nлев. и Nправ. проводят для 20 точек, находящихся в середине кольцевой полосы. Результаты измерений записывают в табл.1. 3. Рассчитывают значения радиусов колец по формуле: rn = [(Nправ)n – (Nлев)n]∙a/2. Здесь а – цена деления окулярной шкалы микроскопа, равная 2∙10–5м. Результаты расчётов заносят в таблицу. 4. Для трёх пар колец (например, для пар 1-4, 2-5, 3-6) по формуле (1) рассчитывают три значения радиуса кривизны линзы, его среднее значение и его погрешность. При расчётах использовать значение длины волны красного светофильтра λ = (640±20) нм. 5. Вычислить радиус кривизны линзы графическим методом. Для этого необходимо построить зависимость rn2 от порядка интерференционного кольца n (на миллиметровой бумаге), которая должна представлять собой прямую линию. Из наклона прямой можно определить радиус кривизны линзы, так как согласно формуле (6): tgα = (rm2 – rn2 )/(m – n) λ = R . Таблица. Отсчёты по окулярной шкале и радиусы колец Ньютона λ = 640 нм; а = 2∙10–5 м. Отсчёты в делениях шкалы Номера колец Радиусы колец Nлев. Nправ. 1 2 … Вопросы для самопроверки 1. Почему в опытах с тонкими пластинами интерференционные полосы хорошо видны в отражённом свете и при использовании протяжённых источника белого света. 2. Почему кольца Ньютона можно назвать полосами равной толщины. 3. Что произойдет с картиной колец, если пространство между линзой и пластиной заполнить водой? 4. Почему при наблюдении колец в отражённом свете в центре картины получается тёмное пятно? 21 5. Почему при расчёте интерференционной картины не учитывают отражение от передней (плоской) поверхности линзы? 6. Что будет наблюдаться в отражённом свете в центре интерференционной картины, если в опыте на рис. 1 n1 = 1,5; n2 = 1,6; n3 = 1,7. Литература 1. СивухинД.В. Общий курс физики. М.: Физматлит, 2007. Т. IV. Оптика. Гл. III. 2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Академия, 2007, §31.1–§31.3. Работа № 3 Определение периода дифракционной решетки при помощи HeNe лазера. Цель работы Определение периода дифракционной решетки при помощи He-Ne лазера. Приборы и принадлежности Дифракционная решетка, He-Ne лазер, линейка, экран. Теоретическое обоснование Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с неоднородностями, которая приводит к отклонениям от законов геометрической оптики. В частности, дифракция проявляется при огибании световой волной малых препятствий, что приводит к ее проникновению в область геометрической тени. Дифракционная решетка представляет собой систему параллельных одинаковых щелей, расположенных на равных расстояниях друг от друга. Решетки могут работать на пропускание света – в этом случае дифракционная картина наблюдается в проходящих лучах. Широко распространены также металлические отражательные решетки, дающие дифракционную картину в отраженных лучах. Простейшая дифракционная решетка, работающая на пропускание света, представляет собой стеклянную пластинку, на которой, с помощью делительной машины, алмазным резцом нанесен рад параллельных штрихов. 22 Эти штрихи образуют непрозрачные промежутки между неповрежденными участками пластины, которые и выполняют роль щелей. Расстояние между серединами соседних щелей называется периодом или постоянной решетки. Период решетки d равен сумме ширины непрозрачного промежутка a и ширины щели b: d = а+b. Эта величина является одной из основных характеристик дифракционной решетки. Пусть на дифракционную решетку падает плоская монохроматическая волна и фронт волны параллелен плоскости решетки – дифракция Фраунгофера в параллельных лучах, когда источник света и точка наблюдения расположены достаточно далеко от препятствия (рис. 1). Тогда по принципу Гюйгенса каждая точка щели становится самостоятельным источником вторичных волн, распространяющихся по всем направлениям. При этом световые лучи отклоняются от первоначального направления на различные углы дифракции , огибают препятствия – непрозрачные промежутки – и заходят в область геометрической тени. Дифракционная картина, возникающая от решетки, наблюдается или в бесконечности, или в фокальной плоскости линзы Л на экране Э. Лучи дифрагирующие под одинаковыми углами , собираются линзой в некоторой точке Р экрана. Рис. 1. Дифракция Фраунгофера на решётке. Принцип Гюйгенса-Френеля позволяет рассчитать интенсивность света в различных точках экрана. Согласно этому принципу, интенсивность в данной точке экрана J p ~ Ap2 , где Ар – результирующая амплитуда колебаний, пришедших в точку Р от всех щелей решетки. Результирующая амплитуда колебаний Ар является векторной суммой амплитуд колебаний создаваемых в точке Р каждой щелью: Ар А1 А2 А3 N АN Аi . i 1 Модули всех этих векторов одинаковы и зависят от угла . Для тех углов , для которых разность хода лучей d sin удовлетворяет условию: d∙sinm = ±m 23 где m = 0, 1, 2, 3, … и т.д., колебания, приходящие в точку Р от отдельных щелей, усиливают друг друга и амплитуда в точке Р будет максимальна. Формула (1) определяет положение главных максимумов интенсивности, целые числа m называются порядком главного максимума. Главные максимумы располагаются симметрично по обе стороны относительно центрального главного максимума нулевого порядка (m=0, точка F на рисунке 1). При освещении решетки монохроматическим светом с длиной волны , главные максимумы имеют вид светлых полос, цвет которых определяется длиной волны падающего света. Если на решётку падает луч лазера с малым углом расходимости, то дифракционная картина представляет собой систему светлых пятен красного цвета убывающей интенсивности ( = 0,6328 мкм – длина волны излучения He-Ne лазера). Более подробно теория дифракционной решетки изложена в лабораторной работе № 8. Измерив величины m в различных прядках m по формуле (1) можно определить период дифракционной решётки d по известной длине волны и наоборот. Формулу (1) можно представить как sinm = m d (2) для абсолютных значений m и m, т.е., синус угла дифракции пропорционален порядку главного максимума с коэффициентом пропорциональности d. Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Допустим, что имеется N пар измеренных значений (х1,у1), (х2,у2), …, (хN,уN). Найденные значения откладываются на графике. Затем ищется зависимость вида y = kx, которая проходила бы как можно ближе к экспериментальным точкам. Составим величину φ – сумму квадратов отклонений N точек от прямой 2 𝜑 = ∑𝑁 𝑖=1(𝑦𝑖 − 𝑘𝑥𝑖 ) Величина φ всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для коэффициента пропорциональности k следует выбирать такое значение, при котором φ имеет минимум 𝑑𝜑/𝑑𝑘 = −2 ∑𝑁 𝑖=1 𝑥𝑖 (𝑦𝑖 − 𝑘𝑥𝑖 ) = 0, 𝑘 = ∑𝑁 𝑖=1 𝑥𝑖 𝑦𝑖 откуда /∑ 𝑁 2 𝑖=1 𝑥𝑖 . (3) 24 Вычисление показывает, что среднеквадратичная ошибка определения величины k равна при этом 𝑁 1 √ (∑(𝑦𝑖 − 𝑘𝑥𝑖)2 (𝑁 − 1) 𝑖=1 Sk / 𝑁 ∑ 𝑥𝑖 2 ) 𝑖=1 = . (4) Обозначим наибольший из главных максимумов, который может наблюдаться в нашем эксперименте через N. Тогда коэффициент пропорциональности в формуле (2) d ,согласно (3), может быть вычислен по экспериментально измеренным значениям синусов углов дифракции sinfm главных максимумов 𝑁 𝜆 = ∑ 𝑚 ∙ s𝑖𝑛 𝜑𝑚 𝑑 𝑚=1 𝑁 /∑𝑚 2 . (5) 𝑚=1 По формуле (5), в методе наименьших квадратов можно найти по известному периоду решётки d; если наоборот, известна величина , то можно рассчитать период решётки d. В первом случае среднеквадратичная ошибка измерения длины волны, согласно (4), будет равна: 𝜆 2 𝑁 ∑ (sin 𝜑 − 𝑚) 1 𝑚 𝑚=1 𝑑 𝑆𝜆 = 𝑑 √ ( ). 2 (𝑁 − 1) ∑𝑁 𝑚 𝑚=1 (6) Во втором случае среднеквадратичная ошибка измерения периода решётки d, согласно формуле (4): Sd = (d)∙ Sλ . (7) В формулах (6) и (7) одна из величин (, d) задана, а другая определяется по формуле (5). Порядок выполнения работы 25 1. Соберите установку согласно рис. 2, дифракционную решётку между ними. установите лазер, экран и Рис. 2. Установка для измерения периода дифракционной решётки. 1 – He-Ne лазер, 2 – дифракционная решетка, 3 – экран для наблюдения. В схеме не используется линза, так как при постоянной решётки d ≈ -5 0,01мм =10 м достаточно расположить экран наблюдения от решётки на расстоянии L >> πd2/λ ≈ 0,005м , (8) чтобы выполнялось условие дифракции Фраунгофера. 2. Получите на экране чёткую картину дифракционных спектров нескольких порядков, установив приблизительно симметричное расположение спектров относительно нулевого максимума. 3. Установите экран на таком расстоянии от дифракционной решётки, чтобы можно было наблюдать максимальное число порядков в спектре – до семи (см. рис. 2). экран максимум 3 порядка максимум 2 порядка дифракционн ая решетка максимум 1 порядка нулевой порядок лазерный луч Рис. 2. Схема измерений. 26 4. Измерьте расстояние l от экрана до дифракционной решетки (согласно оценке (8) оно должно быть больше 0,5 см.). 5. Измерьте расстояния x+m и x–m для всех наблюдаемых порядков и вычислите средние расстояния xm = (x+m + x–m)/2 дифракционных максимумов порядка n от нулевого максимума. Результаты занесите в таблицу. Обработка результатов измерений 1. Из рисунка 2 следует, что: sinfm = xm/( xm2 + l2)1/2 , где fm – угол дифракции m –го порядка. Рассчитайте величины sinfm и внесите их в таблицу. 2. Постройте график зависимости sinfm от порядка спектра m. Угол наклона этого графика относительно оси абсцисс, согласно (2), равен d Вычислив это отношение по формуле (5), рассчитайте постоянную решётки 𝑑̅. 3. Определите среднеквадратичную погрешность измерения периода решётки по формуле (7). 4. Для вероятности (надежности) = 0,95, по таблице коэффициентов Стьюдента (см. Приложение) для N = 7, находим t,N = 2,45 и определяем абсолютную погрешность Δd = t,N∙Sd . Здесь tα,N – коэффициент Стьюдента, в котором: N –число наблюдаемых в нашем эксперименте спектров, α – вероятность того, что постоянная решётки d находится в интервале 𝑑̅ ± Δd. 5. Определите относительную ошибку измерений по формуле: Ed = Δd/𝑑̅∙100%. 6. Результаты измерения округлите с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности. 7. Представьте результат измерений в виде: d = 𝑑̅ ± Δd . Таблица l, мм = … № спектра x+m x–m xm = (x+m + x–m)/2 m 1 2 3 27 sinfm 𝑑̅ Δd Ed 4 5 6 7 Вопросы для самопроверки 1. Для большинства оптических расчетов можно с успехом пользоваться законами геометрической оптики, в частности таким понятием как световой луч. А когда понятие светового луча теряет смысл? Иными словами, какова предельная толщина светового луча? 2. В чём состоит принцип Гюйгенса-Френеля? 3. Какой максимальный порядок спектра может наблюдаться с помощью дифракционной решётки, использованной в данной работе? 4. Чем определяется, будет ли число зон Френеля, открываемых щелью чётным или нечётным? 5. Как изменится дифракционная картина, если увеличить общее число штрихов решётки, не меняя постоянную решётки? 6. Определить число штрихов на 1 мм дифракционной решётки, если углу /2 соответствует максимум пятого порядка для монохроматического света с длиной волны 0,5 мкм. Литература 1. Трофимова Т.И. Курс физики. М.: Академия, 2008. § 180,181. 2. Савельев И.В. Курс общей физики. Кн. 4. СПб.: Лань, 2008. § 5.5, 5.6. Приложение. n 2 3 4 5 6 7 8 9 0.6 1.376 1.061 0.978 0.941 0.920 0.906 0.896 0.889 Коэффициенты Стьюдента Значения α 0.8 0.95 0.99 3.078 12.706 63.657 1.886 4.303 9.925 1.638 3.182 5.841 1.533 2.776 4.604 1.476 2.571 4.032 1.440 2.447 3.707 1.415 2.365 3.499 1.397 2.306 3.355 28 0.999 636.61 31.598 12.941 8.610 6.859 5.959 5.405 5.041 n 10 0.6 0.883 Коэффициенты Стьюдента Значения α 0.8 0.95 0.99 1.383 2.262 3.250 0.999 4.781 Работа № 4 ИЗУЧЕНИЕ ЗАКОНА ОСВЕЩЁННОСТИ Цель работы Установить зависимости освещённости поверхности от расстояния до точечного источника света и угла падения световых лучей на поверхность. Приборы и принадлежности Оптическая скамья со светонепроницаемым корпусом, на которой установлен осветитель с лампой (U=36 В); регулируемый источник питания (U=36 В); фотоэлемент; микроамперметр. Теоретическое обоснование Электромагнитные волны переносят энергию. Количество переносимой энергии в единицу времени через единичную площадку называется потоком энергии электромагнитных волн Фэ и измеряется в ваттах (Вт). Наряду с энергетической оценкой света используется оценка, основанная на непосредственном световом восприятии глаза. Поток электромагнитной энергии, оцениваемый по зрительному ощущению, называется световым потоком Ф и измеряется в люменах (лм). Реальная электромагнитная волна представляет собой набор волн с длинами, непрерывно распределёнными в некотором диапазоне ∆λ. В белом свете ∆λ охватывает весь диапазон, воспринимаемых глазом электромагнитных волн от 0,40 до 0,76 мкм. Действие света на глаз (световое ощущение) при данном потоке энергии, переносимой электромагнитной волной, зависит от длины волны. Чувствительность глаза к свету различной длины волны даётся кривой относительной спектральной чувствительности (рис.I). 29 Рис. 1. ЧУВСТВИТЕЛЬНОСТЬ ГЛАЗА К СВЕТУ Различного ЦВЕТА. Так изменяется доля света, воспринимаемая глазом человека. Свет с длиной волны менее 0,38 мкм называется ультрафиолетовым, а с длиной волны более 0,78 мкм - инфракрасным. И тот и другой диапазон невидимы для человеческого глаза. По горизонтальной оси отложена длина волны λ, по вертикальной оси – относительная спектральная чувствительность (относительная световая эффективность) V(λ). Функция V(λ) – безразмерная величина и максимальна для длины волны λ 0 = 0,555 мкм (зелёный цвет). Значение функции при этой длине волны принято за 1. Как видно из рис.1, для более длинных 0 и более коротких волн 0 чувствительность быстро уменьшается. Так, для λ = 0,51 мкм и λ = 0,61 мкм чувствительность уменьшается вдвое. Это означает, что для получения зрительного ощущения такой же интенсивности свет данной длины волны должен иметь плотность потока энергии в два раза большую, чем свет, для которого V(λ 0 ) = 1. Пусть dФэ – поток энергии, приходящийся на длины волн от λ до λ+∆λ. Тогда световой поток dФ в этом же интервале длин волн будет определяться по формуле: dФ = V(λ) dФэ. Это и определяет световой поток как поток световой энергии, оцениваемый по зрительному ощущению. Наиболее просто световые величины определяются для точечного источника, размеры которого малы по сравнению с расстоянием до точки наблюдения и который посылает световой поток равномерно во все стороны. Излучение называется равномерным (изотропным), если в одинаковые телесные углы1), выделенные по любому направлению, излучается одинаковая мощность. Выделим в некотором направлении от точечного источника света элементарный телесный угол dΩ. Если в пределах этого телесного угла распространяется световой поток dФ, то величина I = dФ/dΩ называется силой света источника в данном направлении. Сила света численно равна световому потоку, приходящемуся на единичный телесный угол. Для изотропного источника элементарный телесный угол dΩ можно заменить конечным телесным углом Ω и получить Ф = I∙Ω. Из этого равенства следует, что полный световой поток Ф, излучаемый изотропным источником силой света I во всех направлениях равен: Ф = 4πI. Единица силы света – кандела (кд) является основной световой единицей в Международной системе (СИ). 1) Телесный угол измеряется отношением площади той части сферы с центром в вершине конической поверхности, которая вырезается этим Телесным углом, к квадрату радиуса R сферы. Единицей измерения Телесного угла является стерадиан. Освещённость поверхности Е есть отношение светового потока, падающего на элемент поверхности, к площади этого элемента: 30 Е = dФ/dS. Если площадка dS расположена внутри телесного угла dΩ и нормаль к ней составляет угол α с направлением светового потока, то её величина связана с величиной аналогичной площадкой dS0, перпендикулярной световому потоку, соотношением dS0 = dS∙cosα. В этом случае для телесного угла dΩ получим dΩ = dS0/R2 = dS∙cosα /R2. Здесь R – расстояние от поверхности до источника. Воспользовавшись определениями для силы света I и освещённости Е и полученным соотношением для элементарного телесного угла dΩ, выражение для освещённости преобразуется следующим образом: Е = dФ/dS = dФ ∙cosα /dS0 = dФ ∙cosα/dΩ∙R2 = I ∙cosα/R2. Это равенство и выражает закон освещённости: освещённость, создаваемая точечным источником на площадке dS, равна силе света, умноженной на косинус угла падения света на площадку и делённой на квадрат расстояния до источника. Единицей освещённости является люкс (лк), равный освещённости, создаваемой потоком в 1 лм, равномерно распределённом по поверхности площади 1 м2. Описание установки. Для проведения измерений используется установка (рис.2), состоящая из оптической скамьи 1 с разъёмным светонепроницаемым корпусом 2 и камеры 3, в которой смонтирован селеновый фотоэлемент с запирающим слоем. Рис. 2. Общий вид измерительной установки. Селеновый фотоэлемент состоит из металлической подложки, на одной стороне которой нанесён слой селена толщиной около 0,1 мм (рис.3). Этот слой покрыт полупрозрачным электродом, прозрачным в видимой части спектра. Внутренний фотоэффект возникает вблизи контактного слоя между полупроводником (селеном) и металлом и приводит к возникновению фото-эдс. Сила тока, регистрируемая микроамперметром 31 (рис.3), будет пропорциональна фото-эдс, т.е., световому потоку, падающему на фотоэлемент. Изменяя расстояние от фотоэлемента до источника и его ориентацию относительно светового потока можно изучать зависимости, описываемые законом освещённости. мкА + + + + + + + + + + селен _ _ _ _ _ _ _ _ _ _ металл + _ Рис.3. Подключение микроамперметра к фотоэлементу. Подготовка прибора к работе 1. Перед проведением измерений к зажимам фотоэлемента 4 (рис.2) подключается микроамперметр с соблюдением необходимой полярности подключения. 2. Фотоэлемент должен быть установлен перпендикулярно оси прибора, при этом ручка 5 (рис.2) должна находиться на нулевой отметке угловой шкалы прибора 6. 3. Стойка с лампой накаливания 8 (рис.2) устанавливается на оптической скамье так, чтобы нить накала лампы находилась на геометрической оси камеры и, следовательно, фотоэлемента. Стойка с лампой может перемещаться вдоль оси корпуса в пределах шкалы с делениями 7 (рис.2). При этом нулевое деление шкалы совпадает с плоскостью чувствительного слоя фотоэлемента, а указатель на стойке осветителя 8 – с плоскостью светящейся точки. Осветитель подключается к блоку питания с регулируемым напряжением 36 В. 4. Приближая или удаляя источник света, необходимо убедиться, что стрелка микроамперметра отклоняется тем больше, чем ближе источник к фотоэлементу. При минимальном расстоянии источника от фотоэлемента с помощью регулируемого источника напряжения необходимо установить ток микроамперметра не менее 90 микроампер. Порядок выполнения измерений 1. При показаниях угловой шкалы фотоэлемента 00 снять десять показаний микроамперметра i для различных расстояний R между освещаемой поверхностью (фотоэлементом) и осветителем. Результаты занести в таблицу. 32 2. Повторить измерения для показаний угловой шкалы 300, 450 и 600. Полученные результаты занести в таблицу. Обработка результатов измерений 1. Откладывая на оси абсцисс 1/R2, на оси ординат i, построить графики зависимости показаний микроамперметра от обратного квадрата расстояния между освещаемой поверхностью и источником света для различных значений α, указанных в таблице. Кривые для различных углов α выполнить на одном графике на миллиметровой бумаге. 2. Рассчитать коэффициент линейной корреляции r1) между переменными 1/R2 и i для кривой, соответствующей углу α = 0. 3. Откладывая на оси абсцисс cosα, на оси ординат i, построить график (на миллиметровой бумаге) зависимости показаний микроамперметра от косинуса угла между нормалью к плоскости фотоэлемента и осью прибора. Значения i выбираются для фиксированного минимального расстояния от фотоэлемента до источника света одинакового для различных углов. 4. Рассчитать коэффициент линейной корреляции r между переменными cosα и i. 1) КОРРЕЛЯЦИЯ ЛИНЕЙНАЯ - статистическая линейная связь непричинного характера между двумя количественными переменными х и у. Является результатом деления ковариации на стандартные отклонения обеих переменных: , где sxy - ковариация между переменными х и у; sx, sy - стандартные отклонения для переменных х и у; xi, yi - значения переменных х и у для объекта с номером i; x, y - средние арифметические для переменных х и у. Коэффициент корреляции r может принимать значения из интервала [-1; +1]. Значение r = 0 означает отсутствие линейной связи между переменными х и у (но не исключает статистической связи нелинейной). Положительные значения коэффициента (r > 0) свидетельствуют о прямой линейной связи; чем ближе его значение к +1, тем сильнее связь статистическая прямая. Отрицательные значения коэффициента (r 0) свидетельствуют об обратной линейной связи; чем ближе его значение к 1, тем сильнее обратная связь. Значения r = ±1 означают наличие полной линейной связи, прямой или обратной. В случае полной связи все точки с координатами (xi, yi) лежат на прямой y = a + bx. Общая классификация корреляционных связей сильная, или тесная при коэффициенте корреляции r>0,70; средняя при 0,50<r<0,69; умеренная при 0,30<r<0,49; слабая при 0,20<r<0,29; очень слабая при r<0,19. Таблица Номер опыта α=00, cosα =1 i R 1/R2 α=300, cosα =0,87 i R 1/R2 1 33 α=450, cosα =0,71 i R 1/R2 α=600, cosα =0,5 i R 1/R2 2 3 . . . 10 Вопросы для самопроверки 1. Чем отличаются энергетические и световые величины в фотометрии. 2. Какая световая единица является основной в Международной системе единиц (СИ)? 3. Назовите все световые единицы. 4. Какой физический смысл пропорциональности освещённости косинусу угла падения света и обратной пропорциональности квадрату расстояния до источника? 5. На какой высоте h над центром круглого стола радиусом r = 1 м нужно повесить лампочку, чтобы освещённость на краю стола была максимальной? 6. По обе стороны от точечного источника света на одинаковом расстоянии 1 м помещены экран и плоское зеркало, плоскости которых параллельны. Какова освещённость в центре экрана, если сила света источника I = 2 кд? 7. Две электрические лампочки поставлены рядом и расстояние от них до экрана 1 м. Насколько нужно приблизить экран, чтобы освещение не изменилось, если одну лампочку погасили? Литература 1. Савельев И.В. Курс общей физики. Спб, Лань, 2008, кн. 4, §5.5 – 5.6. 2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Академия, 2007, §32.3 – 31.3. 3. Трофимова Т.И. Курс физики. М.: Академия, 2008, §168. Работа № 5 ИЗУЧЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА. ЗАКОН МАЛЮСА. Цель работы Ознакомление с методами получения и анализа поляризованного света и проверка закона Малюса. Приборы и принадлежности Поляризатор, анализатор, источник света, фотоэлемент, микроамперметр. Теоретическое обоснование 34 Естественный и поляризованный свет. Известно, что световые волны поперечны: электрический вектор Е и магнитный вектор Н (или В) взаимно перпендикулярны и располагаются в плоскости, перпендикулярной направлению распространения волны – волновому вектору k, с которым в каждый момент времени образуют правую тройку векторов (рис. 1). В любой данной точке пространства ориентация пары векторов Е и Н в плоскости, перпендикулярной лучу (вектору k) может, вообще говоря, изменяться со временем. В зависимости от характера такого изменения различают естественный и поляризованный свет. Обычные источники света являются совокупностью очень большого числа быстро высвечивающихся (10-10 ÷ 10-9 с) элементарных источников (атомов или молекул), испускающих свет независимо друг от друга с разными фазами и с разными ориентациями векторов Е и Н относительно волнового вектора. Поэтому в результирующей волне ориентация векторов Е и Н хаотически изменяется во времени, так что в плоскости, перпендикулярной лучу, все направления оказываются в среднем равноправными. Такой свет называется естественным или неполяризованным. При помощи специальных устройств (поляризаторов) естественный свет может быть превращён в линейно поляризованный (или плоско поляризованный). В линейно поляризованной световой волне пара векторов Е и Н не изменяет с течением времени своей ориентации. Плоскость E, k называется в этом случае плоскостью колебаний1. ____________________________ Говоря о направлении световых колебаний, мы направление колебаний электрического (светового) вектора. 1 будем подразумевать Наиболее общим типом поляризации является эллиптическая поляризация. В эллиптически поляризованной световой волне конец вектора Е (в данной точке пространства) описывает некоторый эллипс. Линейно поляризованный свет можно рассматривать как частный случай эллиптически поляризованного света, когда эллипс поляризации вырождается в отрезок прямой линии; другим частным случаем является круговая поляризация (окружность - частный случай эллипса). При теоретическом рассмотрении различных типов поляризации удобно проектировать вектор Е в некоторой точке пространства на два взаимно перпендикулярных направления (рис. 2). В том случае, когда исходная волна была поляризованной, Ех и Еу когерентны между собой 35 (т.е. колеблются с одинаковой частотой) и могут быть записаны в виде: Ex = Ex0cos (kz – ωt), Ey = Ey0cos (kz – ωt – φ), (1) где амплитуды Ex0, Ey0, волновой вектор k, частота ω и сдвиг фаз φ не зависят от времени. Формулы (1) описывают монохроматический свет. Немонохроматический свет может быть представлен суммой выражений типа (1) с различными значениями частот w. Ориентация эллипса поляризации определяется отношением амплитуд Ey0/Ex0 и разностью фаз φ. В частности, при φ = 0, ±𝜋 эллипс вырождается в отрезок прямой (линейная поляризация). При φ = ±𝜋/2 главные оси эллипса совпадают с осями х, у. Если при этом отношение амплитуд Ey0/Ex0 = 1, эллипс поляризации вырождается в окружность. В плоскости z = z0 вектор E волны (1) вращается против часовой стрелки (при наблюдении навстречу волне), если 0< φ < π. В этом случае говорят о левой эллиптической поляризации волны. Если же π< 𝜑 < 2π, вращение вектора Е происходит по часовой стрелке, и волна имеет правую эллиптическую поляризацию. В фиксированный момент времени t = t0 концы вектора Е при различных z лежат на винтовой линии. При этом для левой эллиптической поляризации образуется левый винт, а для правой – правый винт (рис. 3). Неполяризованный свет также может быть разложен на две линейно поляризованные компоненты; однако в этом случае разность фаз испытывает быстрые хаотические изменения, так, что колебания Ex и Ey оказываются некогерентными. Методы получения линейно поляризованного света. Для получения линейно поляризованного света применяются специальные оптические приборы – поляризаторы. Направление колебаний электрического вектора в волне, прошедшей через поляризатор, называется плоскостью поляризации (или плоскостью пропускания) поляризатора. Любой поляризатор может быть использован для исследования поляризованного света, т.е. в качестве анализатора. Интенсивность линейно поляризованного света I после прохождения через анализатор зависит от угла, образованного плоскостью колебаний с плоскостью поляризации анализатора: I = I0cos2α. (2) Соотношение (2) носит название закона Малюса. Для получения полностью или частично поляризованного света используется одно из трёх физических 36 явлений: 1) поляризация при отражении света или преломлении света на границе раздела двух прозрачных сред; 2) линейный дихроизм; 3) двойное лучепреломление. Отражение света от диэлектрической пластинки. Отражённый от диэлектрика свет всегда частично поляризован. Степень поляризации света, отражённого от диэлектрической пластинки в воздух, зависит от показателя преломления диэлектрика n и от угла падения i. Как следует из формул Френеля, полная поляризация отражённого света достигается при падении под углом Брюстера, который определяется соотношением tg i = n. (3) В этом случае плоскость колебаний электрического вектора в отражённом свете перпендикулярна плоскости падения2. Преломление света в стеклянной пластинке. Поскольку отражённый от диэлектрической пластинки свет оказывается частично (или полностью) поляризованным, проходящий свет также частично поляризуется. Преимущественное направление колебаний электрического вектора в прошедшем свете совпадает с плоскостью преломления луча. Максимальная поляризация проходящего света достигается при падении под углом Брюстера, Для увеличения степени поляризации преломлённого света используют стопу стеклянных пластинок, расположенных под углом Брюстера к падающему свету. ______________________________ Плоскость падения проходит через падающий луч и нормаль к отражающей поверхности в точке падения. 2 Преломление света в двоякопреломляющих кристаллах. Некоторые кристаллы обладают свойством двойного лучепреломления. Это связано с различием поляризуемости молекул в разных направлениях (диэлектрическая проницаемость определяет показатель преломления среды n). Двоякопреломляющий кристалл называют одноосным, если в нём существует одно направление с экстремальным значением , а в других (перпендикулярных) направлениях значения одинаковы (тензор диэлектрической проницаемости образует эллипсоид вращения). Направления вдоль осей эллипсоида называют главными, а одно из них – с экстремальным значением – оптической осью. Линейно поляризованная волна, в которой вектор Е перпендикулярен оптической оси, называется обыкновенной; если же вектор Е имеет проекцию на оптическую ось, это необыкновенная волна. Показатели преломления этих волн обозначают через n0 (ординарная волна) и ne (экстраординарная)3. Преломляясь в таких кристаллах, световой луч разделяется на два луча со взаимно перпендикулярными плоскостями колебаний, Отклоняя один из лучей в сторону, можно получить плоско поляризованный свет, – так устроены поляризационные призмы (Николя, Глана). 37 Поглощение света в дихроических пластинках. У некоторых двоякопреломляющих кристаллов (например, турмалина) коэффициенты поглощения света для двух взаимно перпендикулярно поляризованных лучей отличаются настолько сильно, что уже при небольшой толщине кристалла из него выходит линейно поляризованный пучок света. Это явление носит название дихроизма. Дихроические пластинки изготовляются в виде тонких плёнок, закрытых стёклами – поляроидов. Если поляроиды используются для создания поляризованного света, их называют поляризаторами, если для определения характера поляризации – анализаторами. Рассмотрим прохождение естественного света последовательно через два идеальных поляроида П1 и П2 (рис. 4), плоскости пропускания которых развернуты на некоторый угол φ. Естественный свет можно представить как совокупность одинаковых по интенсивности линейно поляризованных волн, электрические вектора которых совершают колебания во взаимно перпендикулярных направлениях: I0 = I' + I''. И пусть поляризация волны с интенсивностью I' (амплитуда Е' ≈ √I′ ) совпадает с направлением yy' первого поляроида (рис. 4). Тогда прошедшая через него волна будет иметь ______________________________________ Кристалл, в котором все три оси эллипсоида диэлектрической проницаемости имеют разную величину, 3 называют двуосными. Все волны в нём необыкновенные. интенсивность I' = I0/2, а волна с интенсивностью I'' будет задержана первым поляроидом. Разложим амплитуду уже линейно поляризованной волны Е' на две компоненты: Е'∙cos 𝜑 и Е'∙sin 𝜑 в плоскости второго поляроида П2. Проекция Е'∙cos 𝜑 будет пропущена вторым поляроидом, а Е'∙sin 𝜑 – нет. Таким образом, при прохождении естественного света интенсивности I0 через два поляроида получится линейно поляризованная волна 1 интенсивности I0cos2𝜑 (закон Малюса (2)). 2 38 Рис. 4. Схема ориентировки поляризаторов при проверке закона Малюса. yy' – плоскости пропускания поляроидов. Описание установки и метода измерений Работа выполняется на установке, схема которой приведена на рис.5. Свет от лампы накаливания 1, расположенной в фокусе линзы 3, параллельным потоком проходит через поляризатор 4, анализатор 5 и с помощью линзы 6 фокусируется на поверхности селенового фотоэлемента 7. Возникающий ток регистрируется микроамперметром 8. Электропитание лампы 1 осуществляется от блока 2. Рис. 5. Блок-схема измерительной установки. Если в установке используется лазер (например, Hе-Ne), у которого излучение линейно поляризовано, то в установке кроме лазера остаётся ещё анализатор 5, фотоэлемент 7 и микроамперметр 8. Порядок выполнения работы. 1. Ознакомиться с установкой и убедиться, что световой пучок достигает чувствительной поверхности фотоэлемента. 2. Убедиться в том, что величина фототока при вращении анализатора на 3600 дважды изменяется от нуля до максимума. 3. Измерить значения углов α1 и α2, при которых достигается максимум фототока и соответствующие им значения интенсивности (Imax)1 и (Imax)2 при вращении анализатора на 3600 и в обратную сторону. Записать средние значения измеренных углов и интенсивностей. 4. Установить анализатор в положение α0 = (𝛼1 + 𝛼2 – 1800)/2. 39 5. Записать в таблицу показания микроамперметра, начиная с того, которое соответствует α0, и далее через каждые 150. Измерения проводятся до тех пор, пока угол поворота не изменится на 1800 от начального положения. Таблица α, град. α – α0 , град. Интенсивность I(α – α0)/𝐼𝑚𝑎𝑥 cвета I(α – α0), отн. ед. cos2(α – α0) Обработка результатов измерений 1. Постройте график зависимости I(α – α0)/𝐼𝑚𝑎𝑥 по данным таблицы. 2. На том же графике построить зависимость cos2(α – α0). 3. Построить график: по оси абсцисс значения cos2(α – α0), а по оси ординат – значения I(α – α0)/𝐼𝑚𝑎𝑥 . 4. Рассчитать коэффициент линейной корреляции r между переменными cos2(α – α0) и I(α – α0)/𝐼𝑚𝑎𝑥 . КОРРЕЛЯЦИЯ ЛИНЕЙНАЯ - статистическая линейная связь непричинного характера между двумя количественными переменными х и у. Является результатом деления ковариации на стандартные отклонения обеих переменных: , где sxy - ковариация между переменными х и у; sx, sy - стандартные отклонения для переменных х и у; xi, yi - значения переменных х и у для объекта с номером i; x, y - средние арифметические для переменных х и у. Коэффициент корреляции r может принимать значения из интервала [-1; +1]. Значение r = 0 означает отсутствие линейной связи между переменными х и у (но не исключает статистической связи нелинейной). Положительные значения коэффициента (r > 0) свидетельствуют о прямой линейной связи; чем ближе его значение к +1, тем сильнее связь статистическая прямая. Отрицательные значения коэффициента (r 0) свидетельствуют об обратной линейной связи; чем ближе его значение к -1, тем сильнее обратная связь. Значения r = ±1 означают наличие полной линейной связи, прямой или обратной. В случае полной связи все точки с координатами (xi, yi) лежат на прямой y = a + bx. Общая классификация корреляционных связей сильная, или тесная при коэффициенте корреляции r>0,70; средняя при 0,50<r<0,69; умеренная при 0,30<r<0,49; слабая при 0,20<r<0,29; очень слабая при r<0,19. Вопросы для самопроверки 1. Как ориентированы в пространстве электрический, магнитный и волновой векторы? 2. В чём разница между неполяризованными, плоско поляризованными и поляризованными по кругу электромагнитными волнами? 3. Как получают плоско поляризованные волны? 40 4. Какие волны называют поперечными, а какие продольными? 5. Интенсивность естественного света, пропущенного через два поляризатора, уменьшилась в два раза. Как ориентированы поляризаторы? 6. На поляризатор падает свет, поляризованный по кругу с интенсивностью I0. Какова интенсивность света за поляризатором? 7. Предельный угол полного внутреннего отражения равен 450. Чему равен угол полной поляризации? Литература 1. Сивухин Д.В. Общий курс физики. т.IV. Оптика.- М: Физматлит, 2006. гл.IV, § 46. 2. Савельев И.В. Курс общей физики. Кн 4.-СПб.: Лань, 2008. гл.6. Работа № 6 ИЗУЧЕНИЕ СПЕКТРА ИЗЛУЧЕНИЯ НЕОНОВОЙ ЛАМПЫ С ПОМОЩЬЮ МОНОХРОМАТОРА Цель работы Изучить устройство и принцип действия оптического прибора – монохроматора УМ-2; освоить методику измерения спектров с помощью монохроматора УМ-2 и построить его градуировочный график; определить угловую и линейную дисперсии монохроматора; определить характерные длины волн в спектре излучения неоновой лампы. Приборы и принадлежности Монохроматор УМ-2, ртутная разрядная лампа высокого давления ДРШ – 250 с блоком питания, неоновая лампа МН-5 (ТН-03). Теоретическое обоснование Переменное электромагнитное поле световой волны, распространяющейся в диэлектрической среде, вызывает колебания связанных зарядов, входящих в состав молекул среды. В области частот видимого и ультрафиолетового излучения определяющую роль играют вынужденные колебания внешних, наиболее слабо связанных электронов атомов и молекул, называемых оптическими электронами. В результате вынужденных колебаний, молекулы среды излучают вторичные электромагнитные волны с частотой первичной волны. Поскольку средние расстояния между частицами вещества во много раз меньше длины когерентности света, то вторичные волны когерентны как между собой, так и с первичной волной. Когерентные 41 волны интерферируют между собой, а результат интерференции зависит от соотношения их амплитуд и начальных фаз. Таким образом, в результате интерференции, в однородном изотропном веществе образуется проходящая волна, направление распространения которой совпадает с направлением распространения первичной волны, а фазовая скорость v зависит от частоты. Для любой гармонической волны эта зависимость называется дисперсией. Прохождение световых волн через вещество характеризуют с помощью показателя преломления среды n (как отношение скорости электромагнитных волн в вакууме с к их фазовой скорости v в среде: n = c/ v), через который и определяют дисперсию. Дисперсией света называется зависимость показателя преломления n вещества от длины волны λ (частоты ν) света. Эта зависимость легко обнаруживается, например, при прохождении пучка белого света через стеклянную призму. Зависимость показателя преломления среды от длины волны нелинейная и немонотонная. Области значений, в которых dn ˂0, т.е. с d ростом длины волны показатель преломления убывает, соответствуют нормальной дисперсии света. Нормальная дисперсия наблюдается у веществ, прозрачных для света. Дисперсия света называется аномальной, если dn ˃0, т.е. красные лучи d преломляются сильнее чем фиолетовые. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла эти полосы находятся в инфракрасной и ультрафиолетвой частях спектра. Диэлектрики поглощают свет в основном в областях частот, близких к частотам собственных колебаний электронов в атомах и атомов в молекулах. Наиболее чётко это резонансное поглощение света обнаруживается у разреженных одноатомных газов (например, у паров большинства металлов), для которых характерен линейчатый спектр поглощения света. При этом дискретные частоты интенсивного поглощения света совпадают с частотами собственного излучения возбуждённых атомов этих газов. Каждый газ или пар характеризуется определённым набором линий, составляющих его собственный спектр. Это химических элементов используется в спектральном анализе, для определения химического состава вещества. У газов с многоатомными молекулами и кристаллов наблюдаются системы линий, образующих полосы поглощения, связанных с электронными переходами в молекулах или с межзонными переходами в кристаллах. Такие спектры получили название полосатых. В спектрах простых молекул электронные полосы распадаются на более или менее узкие колебательные полосы и вращательные линии. Вид оптических спектров зависит от состояния вещества. Если вещество находится в термодинамическом равновесии с излучением, то оно 42 излучает сплошной спектр. Распределение энергии в сплошном спектре в зависимости от λ подчиняется закону излучения Планка. Анализ оптических спектров (спектральный анализ) используется для исследования строения и состава вещества. Описание лабораторной установки. Монохроматор – один из спектральных приборов, предназначенных для выделения узких интервалов длин волн (частот) оптического (т. е. видимого, инфракрасного или ультрафиолетового) излучения. Дисперсионным элементом монохроматора служит, либо стеклянная призма, либо дифракционная решетка. В данной работе для анализа спектра неоновой лампы используется монохроматор УМ-2, в котором в качестве дисперсионного элемента используются стеклянные призмы. Монохроматор УМ-2 имеет следующие технические характеристики: рабочий диапазон 380 нм – 1000 нм, фокусное расстояние объектива – 280 мм, цена деления барабанчика щели – 0,01 мм, пределы раскрытия щелей 0-4 мм, преломляющий угол призмы 60 град, градуировка барабана длин волн производится в ходе выполнения лабораторной работы. Внешний вид и оптическая схема этого прибора представлены, соответственно, на рис. 1 и рис.2. Основные части монохроматора коллиматор 3 (рис.1), призменный столик 4 с расположенными на нем призмами 5, выходная труба 6, входная 1 и выходная 8 щели, зрительная труба 7, барабан длин волн 9 и рельс, на котором крепится прибор 10. Рис. 1. Монохроматор УМ-2. 43 Рис. 2. Оптическая схема монохроматора. Коллиматор предназначен для получения параллельного пучка света, падающего на призму. Свет от источника света проходит через входную щель 1 (рис. 2) и узким расходящимся пучком падает на объектив 2. Щель расположена в фокусной плоскости объектива. Из объектива параллельный пучок лучей направляется на призму 3, которая разлагает свет на монохроматические составляющие и одновременно поворачивает световой пучок на 90°. Призма Аббе (3) с преломляющим углом 600 по существу состоит из 2-х тридцатиградусных призм и призмы полного внутреннего отражения между ними. Последняя не участвует в дисперсии, а только поворачивает пучок света на 900. Все три призмы изготовлены из стекла ТФ3 с малым коэффициентом поглощения и склеены канадским бальзамом. В качестве объективов применены ахроматы. Щели спектральных приборов выполняются в виде двух ножей со скошенными краями, направленными по ходу светового пучка, что уменьшает рассеяние света щелью. В монохроматоре применяется равномерная шкала, измеряющая в градусах угол поворота ручки установки длин волн. Приборы, имеющие равномерную шкалу длин волн, нуждаются в проведении градуировки, результатом которой является зависимость λ = f (β), где λ– длина волны, а β отсчёт барабана 9 в градусах (рис. 1). После калибровки, градуировочный график может быть использован для определения длин волн в неизвестных спектрах. Выходная труба предназначается для сортировки световых лучей по их цветности, то есть – для наблюдения какого-то, ограниченного участка оптического спектра. Лучи, например, имеющие определенную длину волны λ1, падают на объектив 4 параллельным пучком и собираются объективом в определенном месте фокальной плоскости. Лучи другой длины волны λ2 44 также параллельны между собой, но они преломляются призмой на несколько иной угол и соответственно падают на линзу 4 под несколько другим углом и поэтому собираются объективом в другом месте фокальной плоскости. Таким образом, в фокальной плоскости зрительной трубы получают спектр, который является цветным изображением входной щели. Выходная щель 5 располагается в фокальной плоскости объектива 4. При повороте призменного столика с помощью барабана длин волн 9 (рис.1) на выходную щель проектируются различные спектральные участки. Спектр может либо визуально наблюдаться с помощью окуляра 7 (рис. 1) (или 6 на рис. 2), либо регистрироваться каким-нибудь регистрирующим устройством. Для установки положения спектральной линии в плоскости выходной щели имеется индекс в виде острия. Индекс наблюдается через окуляр. Вывод спектральной линии на индекс производится с помощью барабана длин волн. Окуляр можно адаптировать по глазу наблюдателя на резкость изображения индекса и спектральной линии путем вращения соответствующей муфты на оправе окуляре. Деления на барабане длин волн нанесены в градусах. При повороте барабана на одно деление (2°), система призм поворачивается на 20``. Чтобы выразить показания шкалы барабана в длинах волн, производят градуировку шкалы барабана. Для этой цели используют в качестве источника света ртутную лампу, дающую линейчатый спектр с известным расположением линий. Совмещая линии спектра с выходной щелью монохроматора, берут отсчеты по барабану длин волн. По этим данным строят градуировочный график: на оси ординат – деления отсчетного устройства, на оси абсцисс – соответствующие длины волн. Таким образом, данная работа состоит из двух частей: градуировки монохроматора и измерения длин волн в видимой части спектра неоновой лампы. Порядок выполнения работы и обработка результатов. I. Градуирование шкалы монохроматора. 1.Укрепить на штативе перед входной щелью монохроматора ртутную лампу и включить ее в сеть. Необходимо так отцентрировать источник света, чтобы объектив коллиматора был равномерно заполнен светом. После чего, с помощью микрометрического винта 2 (рис.1), следует установить ширину входной щели, примерно 0,01 – 0,02 мм. В процессе выполнения работы, с помощью этого винта, можно регулировать яркость и резкость наблюдаемых спектральных линий. Внимание! Во время работы в лампе развивается давление до 30 кгс/см2, поэтому обращаться с ртутной лампой следует осторожно. Ртутная лампа используется в различных оптических приборах для получения узкого пучка 45 света большой интенсивности (1000 Мкд/м2). Излучение лампы имеет линейчатый спектр с непрерывным фоном. Недостатком лампы является длительное время разгорания (2-5 мин.) и остывания после выключения для повторного зажигания. Требуется повышенное напряжение для поджига. На передней панели блока питания лампы имеются выключатель сети, пусковая кнопка и выключатель ртутной лампы. 2. Градуировка выполняется по линейчатому спектру паров ртути. Этот спектр излучается в низковольтном дуговом разряде однозарядными ионами ртути. В таблице 4 указаны: номер, цвет и длины волн для всех линий в спектре ртути в диапазоне видимого света от 400 нм до 710 нм. Красные линии спектра и фиолетовую линию (405 нм) визуально наблюдать сложно, несмотря на относительную яркость последней. Это связано с тем обстоятельством, что их цвета лежат на границах цветового восприятия человеческого глаза. Но при достаточно хорошей настройке прибора их все же удается наблюдать. Надо помнить, что цвет – характеристика достаточно субъективная и то, что один наблюдатель назовет красным (или синим), другой может назвать оранжевым (или фиолетовым). В объектив выходной трубы монохроматора наблюдают спектр в виде чередования цветных полос. Первоначально, поворачивая окуляр необходимо добиться того, чтобы индекс окуляра был установлен параллельно оптическим линиям спектра, т.е. совмещен с ними в вертикальной плоскости. Затем, регулируя уже оправу окуляра, получают четкое изображение спектральной линии и индекса окуляра. Вращая барабан, необходимо последовательно совместить все линии ртути (от красной до фиолетовой) с индексом окуляра, делая при каждом совмещении отсчеты по барабану длин волн. На барабане длин волн нанесены относительные деления – градусы. Отсчет читается против индекса барабана, скользящего по спиральной канавке. Данные заносят в табл. 1. Длины волн излучения ртутной лампы и их относительную яркость берут из табл. 4. Табл. 1. Спектральные линии ртути и соответствующие им отсчеты β по барабану длин волн. № п/п λ, нм 1 2 3 … Яркость β,град 3. По результатам измерений необходимо построить градуировочную кривую λ = f(β), где β – отсчеты по винтовому микрометру, соответствующие длинам волн λ. Градуировочный график строят на миллиметровой бумаге. Масштаб выбирается так, чтобы график позволял 46 определять λ с точностью до 1 нм. Градуировочную кривую проводят плавно с помощью лекала и карандаша. II. Исследование спектра излучения неоновой лампы. 1.Заменить ртутную лампу, стоящую перед входной щелью монохроматора, неоновой лампой. Ширину входной щели установить в пределах 0,01-0,02 мм. Неоновая лампа включается в сеть 220 В. 2. Наблюдая в объектив выходной трубы монохроматора спектральные линии излучения неоновой лампы, необходимо последовательно совместить их с индексом окуляра и произвести отсчеты по шкале барабана длин волн для каждой из 9 линий видимого спектра. Записать яркость отмеченных линий и соответствующие им значения β в табл. 2. Табл. 2. Спектральные линии неона и соответствующие им значения β по барабану длин волн. № п/п Яркость 1 2 3 4 5 6 7 8 9 β,град λ, нм ∆ λ, нм 3. С помощью полученной ранее градуировочной кривой, для найденных значений β определить длины волн, соответствующие этим линиям. Результаты занести в таблицу 2. Сравнить полученные значения длин волн спектра неона с данными таблицы 5. Полученные таким образом абсолютные значения погрешности ∆λ занести в таблицу 2. 4. Определить угловую и линейную дисперсии монохроматора по формулам: D = dφ/dλ (1) D* = fоб∙D (2), где dφ/dλ можно определить с помощью градуировочного графика, fоб – фокусное расстояние объектива коллиматора равное 280 мм. При вычислении дисперсии учесть, что градусы в градуировочной кривой нужно перевести в радианы по формуле: φ = β∙2π/2∙60∙60∙180 (3). Дисперсия спектральных приборов имеет различное значение в разных участках спектра. Поэтому угловое и линейное расстояние между спектральными линиями, отличающимися по длине волны на одну и ту же 47 величину, определяем для 3-x значений длин волн. Результаты заносятся в таблицу 3. Табл. 3 Угловая (по формуле (1) и по градуировочному графику) и линейная дисперсии (по формуле (2)). λ, нм 400 550 700 D, рад/нм D*,рад, 106 Контрольные вопросы: 1. 2. 3. 4. 5. Поясните понятие “спектр излучения”. Какие вы знаете дисперсионные спектральные элементы? На чём основан спектральный анализ? Что такое угловая и линейная дисперсия спектрального прибора? Как объяснить понятие “нормальной” ширины входной щели спектрального прибора? Таблица 4. Спектральные линии ртути с указанием относительной яркости. № п/п 1 2 3 4 5 6 7 8 9 10 11 12 13 Цвет линии Красная -“-“-“Оранжев ая -“-“Желтая -“-“Яркий желтый дублет -“- λ, нм Яркость № п/п 709 708 691 671 20 25 25 16 3 18 19 20 21 22 612 607 587 2 2 2 23 24 25 585 580 579 6 14 100 26 27 28 577 567 24 16 29 30 48 Цвет линии Зеленая -“-“-“-“-“-“Синезеленая -“ -“Синяя яркая -“-“- λ, нм Яркость 529 521 513 512 510 2 2 2 4 2 502 499 492 4 3 10 489 482 436 3 3 400 435 434 40 4 Зеленая Зеленая яркая -“-“- 14 15 16 17 555 546 3 320 31 32 538 535 3 6 33 34 -“Фиолетов ая -“-“- 434 411 30 4 408 405 12 180 Табл. 5. Спектральные линии неона с указанием относительной яркости. № п/п 1 2 3 4 5 6 7 8 9 Цвет линии λ, нм Яркость Ярко-красная Красно-оранжевая, левая из двух близких линий Оранжевая, первая заметная влево от четвертой линии Желтая Светло-зеленая, первая заметная вправо от четвертой линии Зеленая, левая из двух одиноких линий Зеленая, правая из двух одинаковых линий Зеленая, правая из пяти равноудаленных линий 640 100 614 100 594.5 50 585 200 576 40 548 60 533 80 503 50 485 80 Сине-зеленая, одинокая Литература 4. Савельев И.В. Курс общей физики. Спб.: Лань, 2008, кн. 4, §7.1 5. Детлаф А.А., Яворский Б.М. Курс физики. М.:Академия, 2007, §33.4 Работа № 7 ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ПРИЗМЫ С ПОМОЩЬЮ ГОНИОМЕТРА Цель работы Знакомство с работой гониометра, исследование дисперсии стеклянной призмы и определение характеристик призмы как спектрального прибора. 49 Приборы и принадлежности Гониометр, ртутная лампа высокого давления ДРШ – 250 с блоком питания, призма. Теоретическая часть Дисперсией света называется зависимость показателя преломления n вещества от длины световой волны λ (частоты ν), что обусловлено зависимостью фазовой скорости света в веществе от длины волны. Эту зависимость удобно наблюдать при прохождении света через призму. Рассмотрим луч света, распространяющийся симметрично через стеклянную призму (рис. 1). Рис. 1 Преломление в призме. – преломляющий угол призмы (угол при вершине призмы), δ – угол отклонения, i1 , r1 – угол падения и угол преломления на первую грань призмы, i1 , r1 – угол падения и угол преломления на вторую грань призмы. Для того чтобы найти зависимость угла отклонения света от показателя преломления призмы n и ее преломляющего угла , рассмотрим следующую геометрическую задачу. Пусть дан равнобедренный треугольник ∆ABC с углом при вершине (Рис.1а). 50 Рис. 1а Проведем биссектрису BD угла и пусть точка О является центром окружности вписанной в ABC. Опустим из точки О два перпендикуляра ON и OM на стороны AB и BC. Отрезки ON и OM будут равны между собой, как радиусы окружности вписанной в ABC. Теперь соединим прямой точки M и N и рассмотрим OMN и ONM. Поскольку MN является хордой, соединяющей касательные AB и BC, в точках их касания с вписанной окружностью, то MN BD. Следовательно, OMN = OMN = ABD = , 2 как углы с взаимно перпендикулярными сторонами. А значит и BNM =NAD и NM ǁ AC. Теперь рассмотрим луч света, который падает на призму под таким углом, что, после преломления, он распространяется параллельно ее основанию, как показано на рисунке 1б. Восстановим из N и M (точки преломления луча) два перпендикуляра ON, OM и продолжим их за пределы призмы. Тогда i1 и i2 будут углами падения, а r1 и r2 углами преломления (см. рис. 1б). В соответствии, с проведенным выше геометрическим рассмотрением, точка О будет лежать на биссектрисе преломляющего угла призмы, а r1 = i2 = . 2 Учитывая это 1 n обстоятельство, из закона преломления sini1 = n sin r1 и sini2= sinr2 получим i1 = r2. Нас интересует угол отклонения света , который на рисунке 1б возникает как пересечение прямых, являющихся продолжениями направления падения и преломления светового луча. Обозначим , вершину этого угла через K. Из рисунка видно, что, из ∆ NKM, KNM KMN, так как - дополнительный к NKM. Но KNM = i1 r1, а 51 KMN r2 i2 и следовательно i1 . Таким образом i1 и, sin 2 n= sin 2 . (1) 2 Если рассмотреть случай, когда угол падения луча света на призму произволен и тогда луч в самой призме распространяется, вообще говоря, не параллельно основанию, то зависимость, аналогичная (1) будет выглядеть весьма сложно. Теперь, если задаться вопросом: при каком угле падения i1 будет наблюдаться минимальный угол отклонения луча , то оказывается, что минимальное отклонение луча м ин , преломленного призмой, от направления луча, падающего на призму, получается при симметричном ходе луча (луч идёт перпендикулярно биссектрисе преломляющего угла). А это как раз и есть тот случай, для которого мы получили соотношение (1). Показатель преломления материала призмы удобно определять по углу наименьшего отклонения. В данной работе для исследования дисперсии применяется гониометр. С его помощью можно определять показатели преломления и преломляющие углы призм и кристаллов, исследовать параметры дифракционных решеток и т.д. Измерив с помощью гониометра преломляющий угол призмы и углы наименьшего отклонения для монохроматического света различных длин волн, можно по (1) рассчитать величину n и построить дисперсионную кривую – график зависимости n(λ). По дисперсионной кривой могут быть определены такие важные характеристики оптических стёкол, как средняя дисперсия D = nF – nC (2) и коэффициент дисперсии ν (число Аббе): 𝑛 −1 ν = 𝑛 𝐷− 𝑛 . 𝐹 𝐶 (3) Здесь nD, nF и nC – показатели преломления для λD = 589,3 нм (среднее значение длин волн жёлтого дублета натрия), λF = 486,1нм (голубая линия водорода), λС= 656,3 нм (красная линия водорода). Для стёкол возрастание дисперсии идёт обычно параллельно с увеличением удельного веса стекла. Тяжёлые сорта стёкол (флинты) характеризуются большой дисперсией и малым значением ν, лёгкие (кроны) – малой дисперсией и большими значениями ν. По наклону дисперсионной кривой можно оценить разрешающую способность призмы R = λ/δλ = b∙dn/dλ . (4) Здесь δλ – минимальный интервал длин волн, разрешаемый по критерию Релея, и b – размер основания призмы. Формула (4) справедлива при условии, что вся рабочая грань призмы освещена параллельным пучком. 52 Гониометр. Внешний вид гониометра представлен на рис. 3. При освещении входной (коллиматорной) щели ртутной лампой, дающей дискретный спектр, в фокальной плоскости объектива 9 зрительной трубы видны отдельные линии – цветные изображения входной щели (см. рис. 5 и таблицу). Коллиматор гониометра 3, столик 7 и алидада∗ 17 со зрительной трубой 12 крепятся на массивном основании 23. На столике 7 размещаются исследуемые объекты. Коллиматор закреплён неподвижно, а столик и алидада с трубой могут вращаться вокруг вертикальной оси. Ширину коллиматорной щели можно менять от 0 до 2-х мм при помощи микрометрического винта 2, а высоту – от 0 до2-х см – при помощи диафрагмы с треугольным вырезом («ласточкин хвост»), надетой на щель. Винт 4 служит для перемещения объектива 5 – настройки коллиматора на параллельный пучок. Зрительная труба 12 состоит из объектива 9 и окуляра 14 с автоколлимационным устройством 13. Объективы коллиматора и зрительной трубы одинаковы. Фокусировка трубы производится винтом 11. Наклон коллиматора и зрительной трубы к горизонтальной оси изменяется винтами 6 и 10 соответственно. Схема окуляра зрительной трубы с автоколлимационным устройством приведена на рис. 2а. Свет от лампы Л проходит через защитную стеклянную пластинку П и попадает на автоколлимационную сетку А, содержащую две взаимно перпендикулярные щели (рис. 2б). Свет, прошедший через сетку А, попадает на две прямоугольные призмы Р и отражается от гипотенузной грани, на которую нанесён полупрозрачный слой с коэффициентом отражения 50%. Для юстировки гониометра на столик ставится предмет с плоской отражающей поверхностью. После отражения от неё параллельный пучок лучей возвращается назад в зрительную трубу и собирается в фокальной плоскости объектива. В этом случае светящийся крест можно увидеть через окуляр зрительной трубы. Кроме того, в окуляре имеется ещё одна сетка С, ______________________ * Алидада (араб.) – вращающаяся линейка, служит для отсчета углов. 53 Рис. 3. Внешний вид гониометра. на которой изображён чёрный отсчётный крест (рис. 2в). Совмещённые изображения обоих крестов рассматриваются через окулярные линзы О. Резкость видимого изображения отсчётного креста регулируется вращением оправы окуляра 14. Обе сетки окуляра А и С (рис. 2а), расположены на строго одинаковых расстояниях от гипотенузных граней призмы Р, поэтому их одновременное наблюдение в окуляре возможно только при совпадении фокальных плоскостей объектива и окуляра (труба настроена на бесконечность). 54 Важнейшим узлом гониометра является устройство, служащее для отсчёта угла поворота зрительной трубы вокруг вертикальной оси, проходящей через центр столика. На этой оси крепится прозрачное кольцо (лимб), расположенное в корпусе прибора. На поверхности лимба нанесена шкала с делениями. Лимб разделён на 3×360 = 1080 делений. Цена деления 20΄ , оцифровка делений произведена через 10. Шкалу лимба можно наблюдать через окуляр отсчётного устройства 16 при включённой подсветке (тумблер 22). Резкость изображения шкалы регулируется вращением оправы окуляра 15. Оптическая система отсчётного устройства собрана так, что через окуляр можно наблюдать изображения штрихов двух диаметрально противоположных участков лимба, причём одно изображение прямое, а другое обратное (рис. 4). Кроме того, оптическая система позволяет перемещать эти изображения, оставляя в покое, как лимб, так и алидаду со зрительной трубой. Это перемещение штрихов измеряется при помощи оптического микрометра. Шкала микрометра рассчитана таким образом, что при перемещении её на 600 делений верхнее изображение штрихов лимба смещается относительно нижнего на 10΄. Следовательно, цена деления шкалы микрометра 1΄΄. Поле зрения отсчётного микроскопа приведено на рис. 4. В левом окне наблюдаются изображения диаметрально противоположных участков лимба и вертикальный штрих для отсчёта градусов, в правом – деления шкалы оптического микрометра и горизонтальная риска для отсчёта минут и секунд. Для удобства экспериментатора в гониометре предусмотрено несколько вариантов относительного вращения столика, алидады со зрительной трубой и лимба. 1. Алидада вращается относительно лимба либо грубо от руки при свободном винте 24 (см. рис. 3), либо точно с помощью микрометрического винта 25 при зажатом винте 24. 2. Такое же вращение алидады, но вместе с лимбом и столиком, производится, если рычажок 20 находится в нижнем положении. Для возвращении его в верхнее положение надо нажать рычажок 19. 3. Лимб вращается относительно столика и алидады винтом 21 (рычажок 20 в нижнем положении, винт 26 свободен). 4. Вращение столика вместе с лимбом относительно алидады производится либо от руки при свободном винте 26, либо микрометрическим винтом 28 при зажатом винте 26. 5. Столик вращается относительно алидады и лимба либо от руки при свободном винте 27, либо точно микрометрическим винтом 29 при зажатом винте 27 (рычажок 20 в верхнем положении). Гониометр требует тщательной юстировки, которая заключается в установке: а) зрительной трубы на бесконечность; б) поверхности столика и оптической оси трубы – перпендикулярно оси вращения прибора; в) 55 коллиматора – на параллельный пучок лучей; г) оптической оси коллиматора – перпендикулярно оси вращения прибора. Рис. 4. I. Отсчёт углов 1. Глядя в окуляр 15 и, вращая оправу окуляра, настройтесь на резкое изображение лимба (круговой шкалы) и вертикальной шкалы, расположенной справа от лимба. Вращением маховичка оптического микрометра 18 (без усилий!) совместите ближайший к отсчётной риске левый двойной оцифрованный штрих с ближайшим двойным штрихом нижней шкалы. Если совместить штрихи без усилий не удаётся, вращайте маховичёк 18 в другую сторону и совмещайте соседний нижний штрих. Снимите отсчёт угла в градусах – ближайшая верхняя цифра слева от риски (на рис. 1 это 70). Для определения десятков минут просчитайте число интервалов между двойными штрихами от выбранного верхнего до нижнего, отличающегося на 1800 от выбранного верхнего. (На рис. 1 от 7 до 187 между двойными штрихами 5 интервалов, каждый по 10΄, т.е. 50΄). Число минут – это левая цифра вертикальной шкалы над отсчётной горизонтальной риской А (на рис. 1 это 1΄). Число секунд – это отсчёт по правой части вертикальной шкалы (на рис. 1 положение горизонтальной риски А даёт 36΄΄). Положение, показанное на рис. 4, соответствует отсчёту 7 051΄36΄΄. Отсчётное устройство гониометра обеспечивает точность измерения угла не хуже 5΄΄ (по паспорту ГС-5). 56 II. Установка начала отсчёта 2. Расположите трубу против коллиматора. Вращением микрометрического винта 25 (при закреплённом винте 24) совместите двойной отсчётный штрих с ахроматическим изображением входной щели. 3. Для удобства отсчёта можно выставить начальный угол ≅ 1800. Для этого вращением маховичка 18 установите горизонтальную отсчётную риску А на отсчёт 1΄00΄΄. Дополнительная минута рекомендуется потому, что при настройке точно на 0΄0΄΄ (на край шкалы) часто выходит из строя маховичёк 18. Поворачивая нижнюю часть столика сначала от руки при свободном винте 26, а затем микрометрическим винтом тонкой подачи 28 при зажатом винте 26 совместите верхний штрих – 1800 и нижний – 00. При такой настройке все углы, под которыми видны спектральные линии, будут отсчитываться от 001΄00΄΄ – угла падения луча (ось коллиматора под углом ≅ 00). Если настройка на 1800 затруднена, запишите такое начало отсчёта, которое Вы установили. На этом настройка гониометра закончена. Чтобы не сбить начало отсчёта, винт 26 не следует освобождать до конца измерений. Поворачивать столик можно, освобождая только винт 27 (вращается верхняя часть столика без шкалы). В процессе работы полезно уточнять начало отсчёта. Ход работы III. Установка призмы 1. Поставьте рабочую призму так, чтобы её преломляющее ребро было вертикально, а одна из рабочих граней была перпендикулярна одному из установочных винтов 8. 2. Из-за неточного крепления призмы в оправе следует ещё раз подстроить наклон столика: вращая либо алидаду при свободном винте 24, либо столик при свободном винте 27 (винт 26 после установки начала отсчёта освобождать нельзя), найдите отражение светящегося креста от рабочей грани и приведите его к центру винтом 8, перпендикулярным отражающей грани. Трубу наклонять не следует. 3. Установите рабочую грань призмы перпендикулярно второму из винтов 8 и снова найдите отражённый крест. Если крест сместился, его снова следует привести к центру винтом, перпендикулярным отражающей грани. Поверните столик с призмой и проверьте отражение от второй грани и т.д. до тех пор, пока крест перестанет смещаться больше, чем на треть радиуса поля зрения. 57 IV. Измерение преломляющего угла 4. Для измерения преломляющего угла призмы установите трубу перпендикулярно одной из её отражающих граней и снимите отсчёт по лимбу (отсчитайте угол по круговой шкале). Затем, не трогая призму и столик, поверните алидаду с трубой вокруг преломляющего угла призмы и проведите ту же операцию для другой рабочей грани. По углу поворота трубы рассчитайте преломляющий угол призмы. V. Минимальный угол отклонения 5. Для определения минимального угла отклонения δ поставьте призму на столике так, чтобы её основание было параллельно оси коллиматора (на глаз). Расположите лист бумаги за призмой и найдите на нём спектр, вращая столик рукой. Продолжая поворачивать столик рукой и наблюдая за перемещением спектра, найдите положение столика с призмой, соответствующее минимальному отклонению преломлённого луча от направления падающего луча. Рис. 5. Спектр ртутной лампы ДРШ – 250 Таблица. Найдите спектр в зрительную трубу, настройтесь на одну из жёлтых линий (см. рис. 5 и таблицу) и, вращая столик сначала рукой, а затем винтом тонкой подачи 29 при зажатом винте 27, установите его в такое положение, 58 при котором отклонение выбранной спектральной линии от направления оси коллиматора оказывается наименьшим. Для удобства отсчёта можно увеличить высоту входной щели. Если линия видна нечётко, подстройте резкость винтом 11 трубы. Вращая алидаду сначала от руки при освобождённом винте 24, а затем винтом тонкой подачи 25 при закреплённом винте 24, совместите двойной штрих измерительной сетки с выбранной линией и снимите отсчёт по лимбу. 6. Для каждой линии спектра (рис. 5) найдите свой минимум отклонения (своё положение столика с призмой) и определите координату линии. VI. Разрешающая способность 7. Для оценки разрешающей способности призмы измерьте угловую ширину одной из жёлтых линий дублета, предварительно установив минимально возможную ширину входной щели. Если точное измерение ширины линии затруднено, то оцените на глаз, во сколько раз расстояние между линиями дублета больше ширины одной линии. Измерьте линейкой длину b основания призмы. VII. Обработка результатов 1. Рассчитайте минимальные углы отклонения δ(λ) и показатель преломления n(α,δ) по формуле (1). Постройте дисперсионную кривую n(λ). 2. Определите по графику nD, nF и nC и рассчитайте среднюю дисперсию стекла по формуле (2). При определении nC с помощью спектра ртутной лампы дисперсионную кривую приходится несколько экстраполировать в область длинных волн. Рассчитайте число Аббе по формуле (3) и определите по таблицам сорт стекла. 3. По наклону кривой dn/dλ рассчитайте максимальную разрешающую способность призмы по формуле (4). Рассчитайте экспериментальную величину R по измерениям жёлтого дублета и оцените реальный рабочий размер основания призмы. 4. Рассчитайте угловую дисперсию dφ/dλ по измерениям жёлтого дублета. Контрольные вопросы 1. Выведите соотношение (1). 2. В чём состоит явление дисперсии? 3. Что называется нормальной дисперсией света? 4. Что называется аномальной дисперсией света? В каких областях частот наблюдается аномальная дисперсия? 5. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определить угол отклонения луча призмой, если её преломляющий угол равен 300. Литература 59 6. 7. Савельев И.В. Курс общей физики. – СПб.: Лань, 2008, кн. 4, §7.1 Детлаф А.А., Яворский Б.М. Курс физики. М.: Академия, 2007, §33.4 8. Трофимова Т.И. Курс физики. М.: академия, 2008, §185. 60 Работа № 8 ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИФРАКЦИОННОЙ РЕШЁТКИ С ПОМОЩЬЮ ГОНИОМЕТРА Цель работы Знакомство с работой гониометра и определение спектральных характеристик дифракционной решётки. Приборы и принадлежности Дифракционная решётка, ртутная разрядная лампа высокого давления ДРШ – 250 с блоком питания, гониометр. Теоретическая часть Дифракция представляет собой совокупность явлений, наблюдаемых при распространении волн в резко неоднородной среде (например, вблизи границ тела, при прохождении волн сквозь отверстия), когда размеры неоднородностей по величине сравнимы с длиной волны. В случае дифракции Френеля (сферические волны) дифракционная картина создается сходящимися лучами. При дифракции Фраунгофера (плоские волны) лучи распространяются параллельно, поэтому для наблюдения дифракционной картины, на их пути помещают собирающую линзу и устанавливают экран в её фокальной плоскости, как показано на рис. 1. Дифракционная решетка представляет собой строго периодическую структуру, состоящую из N одинаковых щелей шириной b в непрозрачном экране, отстоящих друг от друга на одно и то же расстояние a. Величина d = а b называется периодом решетки (рис. 1). Как правило, дифракционной решёткой служит стеклянная или металлическая пластина, на которую с помощью делительной машины через строго одинаковые интервалы нанесены параллельные штрихи. В учебных лабораториях применяются отпечатки таких гравированных решёток – так называемые реплики, изготовленные из специальной пластмассы. Обычно дифракционная решётка освещается плоской волной, распространяющейся перпендикулярно её поверхности (рис. 1), а плоскость наблюдения практически находится в бесконечности (условия дифракции Фраунгофера). В этом случае направление, в котором производится наблюдение, определяется углом φ между нормалью к решётке и направлением лучей. А распределение интенсивности света, наблюдаемое при дифракции Фраунгофера на решетке, представляет собой интерференционно-дифракционную картину, возникающую как результат 61 суммарной многолучевой интерференции дифракционной картины на каждой щели от всех N щелей. Каждая щель дифракционной решетки в отдельности, для монохроматической волны, дает дифракционную картину, представленную на рис.2. На рисунке изображена зависимость интенсивности волны Iφ от синуса угла , т.е. отклонения волнового вектора от нормали, как показано на Рис. 2. Распределение интенсивности Iφ при дифракции света на одной щели. рис.1. Иными словами, если бы мы закрыли все щели на дифракционной решетке, оставив только одну из них, и поместили экран в фокальную плоскость (как показано на Рис.1), то мы увидели бы напротив этой щели картинку с распределением интенсивности света, как показано на рис.2. 62 Аналитическое выражение для распределения интенсивности в дифракционной картине от одной щели может быть получено на основании принципа Гюйгенса-Френеля, учитывающего интерференцию зон Френеля плоской волны. Эта функция, график которой представлен на рис. 2, равна Iφ = I0 ﴾ 𝜋𝑏 sin 𝑢 2 𝑢 ﴿ (1) где u = sin 𝜑, и характеризует распределение интенсивности в результате 𝜆 дифракции плоской волны на каждой щели. Анализируя выражение (1) на предмет экстремумов, заметим, что при u 0 предел lim sin u =1. Но при u 0 u также и sin 0, а значит и 0 и, следовательно, интенсивность при = 0 равна Iφ = I0. Обратим внимание на тот факт, что условие этого максимума не зависит от длины волны , а, значит, будет справедливо для всех длин волн. Этот максимум интенсивности света соответствует центральному участку спектра, расположенному на пересечении главной оптической оси линзы с ее фокальной плоскостью, независимо от положения щели (точка F на рис. 1). Действительно, условие = 0 означает, что луч перпендикулярен плоскости дифракционной решетки, а, значит, параллелен главной оптической оси линзы. Но точно такое же рассмотрение мы можем провести для каждой щели. Следовательно, лучи от каждой щели, распространяющиеся под углом = 0, соберутся в фокусе линзы, как параллельный пучок света, вне зависимости от их длины волны, и цвет полосы будет белым. Теперь зададимся вопросом: где будут расположены минимумы функции (1)? Очевидно, что нули функции Iφ являются минимумами (поскольку ноль всегда является минимумом квадратичной функции) и совпадают с нулями функции sin u=0 (u=πk, k = ±1; ±2, …; k ≠ 0), при u 0 (иначе (1) теряет 𝜋𝑏 смысл). Принимая во внимание, что u = sin 𝜑, получаем условия для 𝜆 минимумов функции (1) u=πk : bsin 𝜑 = kλ, где – λ длина падающей световой волны. Обратим внимание на тот факт, что условие для минимумов функции Iφ оказывается уже зависимым от длины волны. Таким образом, положение минимумов функции Iφ на экране будет различным для различных длин волн. Несложно сообразить, что между двумя последовательными минимумами должен находиться максимум. Точное положение максимумов можно определить, продифференцировав (1) по и приравняв нулю производную. Теперь мысленно откроем все остальные щели дифракционной решетки. Интенсивность света Iφ, распространяющегося после дифракции на решётке под углом дифракции φ к нормали решетки, состоящей из N щелей, в произвольной точке Р (рис. 1), описывается выражением, которое учитывает как интерференцию волн, приходящих от разных щелей, так и дифракцию на каждой щели: Iφ = I0 ﴾ sin 𝑢 2 sin 𝑁𝛿 2 𝑢 ﴿ ﴾ 63 sin 𝛿 ﴿ , (2) 𝜋𝑑 где δ = sin 𝜑. Множитель I0 определяет величину потока энергии, 𝜆 излучаемого в направлении 𝜑 = 0, т.е. потока энергии недифрагировавшего sin 𝑢 2 света. Множитель ﴾ ﴿ , как мы убедились выше, характеризует 𝑢 распределение интенсивности в результате дифракции плоской волны на sin 𝑁𝛿 2 каждой отдельной щели, а множитель ﴾ ﴿ в формуле учитывает sin 𝛿 интерференцию между пучками, исходящими из всех щелей. График первого сомножителя функции (2) от аргумента sin 𝜑 представлен на рис. 3б (он совпадает с графиком, представленным на рис. 2). Теперь проанализируем поведение интерференционного (второй сомножитель) члена в формуле (2). Как следует из рис. 1, разность хода от соседних щелей равна ∆ = dsinφ (где d период решетки), а интенсивность дифрагированного света максимальна для тех углов φm , для которых волны, собираемые линзой в точке наблюдения от всех щелей решётки, оказываются в фазе. Для всех направлений справедливо интерференционное соотношение: dsinφm = ±mλ (m = 0,1,2,…), (3) где число m даёт порядок главного максимума. Максимум нулевого порядка один, и мы уже обсудили выше, что все лучи с =0 соберутся в центральном максимуме. Все остальные интерференционные максимумы расположены симметрично относительно нулевого (центрального) максимума c левой и правой стороны. Во всех интерференционных максимумах, определяемых условием (3), колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда волны в максимуме возрастает в N раз: А м ак. = NА0, где А0 – амплитуда волны, прошедшей через одну щель. Интенсивность волны I ~ A 2 и, следовательно, I м ак. = N2 I0. Этот результат является следствием интерференции когерентных волн (N некогерентных источников дают интенсивность I м ак. = N I0). Тот же результат можно получить более строго, если с помощью правила Лопиталя посчитать предел sin 𝑁𝛿 2 при sin 0 функции lim ﴾ ﴿ = 𝑁 2 . Но поскольку функция sin sin 𝛿 является периодической, то количество главных интерференционных максимумов будет велико. Побочные интерференционные максимумы могут быть установлены путем дифференцирования по . График функции 1 sin 𝑁𝛿 2 ﴿ представлен на рис. 3а. Из сопоставления рисунков 3а и 3б несложно увидеть, что интерференционные максимумы гораздо уже, чем дифракционные. Действи𝑁2 ﴾ sin 𝛿 64 Рис. 3. Распределение интенсивностей (I/I0) при дифракции света на правильной структуре из N щелей: а) распределение интенсивности, обусловленное интерференцией пучков от разных щелей; б) Распределение интенсивности, обусловленное дифракцией на каждой щели; в) суммарное распределение. тельно, угловая ширина центрального максимума в Nd/b N раз меньше, чем при дифракции на одной щели, что следует из формулы (2). Чтобы получить график функции (2), необходимо перемножить графики 3а и 3б. На рис. 3в представлено суммарное распределение Iφ. Таким образом, максимумы интенсивности дифракционной решетки зависят от числа щелей: Imax = N2Iφ а дифракционная картина выражена тем резче, чем больше число щелей N. Как следует из (3), положение всех главных интерференционных максимумов, кроме нулевого, зависит от длины волны. Поэтому главные максимумы различных длин волн будут разделены на экране; таким образом, дифракционная решетка будет производить разложение немонохроматического излучения на спектральные составляющие, причём фиолетовые лучи будут отклоняются решёткой меньше, чем красные. Входящая в (3) величина m носит название порядка спектра. При m = 0 максимумы интенсивности для всех длин волн располагаются при φ = 0 и накладываются друг на друга. При освещении белым светом нулевой максимум, в отличие от всех прочих, поэтому оказывается неокрашенным. Спектры первого, второго и т.д. порядков располагаются симметрично по обе стороны от нулевого. Основными характеристиками любого спектрального прибора являются дисперсия и разрешающая сила. Угловая дисперсия. Дисперсия D характеризует угловое расстояние между близкими спектральными линиями: 65 𝑑𝜑 D = . 𝑑𝜆 Беря дифференциалы от обеих частей (3), получим: dcosφdφ = m∙dλ. Следовательно, 𝑑𝜑 𝑚 𝑚 D= = = 2 2 2. 𝑑𝜆 𝑑 cos 𝜑 (4) (5) (6) √𝑑 −𝑚 𝜆 Дисперсия возрастает с увеличением порядка спектра. На опыте дисперсию решётки определяют путём измерения углового расстояния ∆φ между двумя близкими спектральными линиями с известной разностью длин волн ∆λ (например, между двумя жёлтыми линиями ртути). Разрешающая способность дифракционной решётки. Возможность разрешения двух близких спектральных линий зависит от их ширины1 и от расстояния между ними. Пусть в спектре m-го порядка наблюдаются две близкие спектральные линии с длинами волн λ и λ + ∆λ. Угловое расстояние ∆φ между этими линиями, согласно (5), равно 𝑚∆𝜆 ∆φ = (7) 𝑑 cos 𝜑 Согласно критерию разрешения Релея два дифракционных максимума воспринимаются раздельно, если середина одного максимума совпадает с краем (минимумом) другого (рис. 4). Такому взаимному расположению разрешаемых максимумов одинаковой интенсивности соответствует пересечение их распределений на уровне половины от максимального значения (рис. 4). Как следует из (2), при переходе из главного максимума (φ = 0) в минимум величина N(kd sinφ)/2 изменяется на π, так что 𝑁𝑘𝑑 2 [sin(φ+dφ) – sin φ] = π, (8) Рис.4. К определению разрешающей способности дифракционной решётки. где dφ – угловая полуширина главного максимума. Принимая во внимание малость dφ, получим из (8) dφ = 𝜆 𝑁𝑑 cos 𝜑 . (9) Отметим, что угловая полуширина максимума обратно пропорциональна Здесь и далее – ширина изображения спектральной линии, определяемая дифракцией, а не её собственная ширина. 1 66 видимому размеру решётки – 𝑁𝑑 cos 𝜑. По определению, разрешающая способность спектрального прибора R = λ/δλ – это отношение длины волны к разности длин волн двух линий, разрешаемых по критерию Релея. Приравнивая δφ (9) и ∆φ (7) для случая предельного разрешения, найдём для дифракционной решётки R= 𝜆 𝛿𝜆 = m∙N . (10) Спектральный интервал δλ, входящий в соотношение (10), характеризует минимальное расстояние между двумя спектральными линиями, которые ещё могут быть разрешены при помощи данной дифракционной решётки. Экспериментальная установка. При работе с дифракционной решёткой основной задачей является точное измерение углов, при которых наблюдаются главные максимумы для различных длин волн. В данной работе для измерения углов используется гониометр Г5, внешний вид которого показан на рис. 5. Коллиматор 3, столик 7 и алидада2 17 со зрительной трубой 12 крепятся на массивном основании 23. На столике 7 размещаются исследуемые объекты. Коллиматор закреплён неподвижно, а столик и алидада с трубой могут вращаться вокруг вертикальной оси. На рис. 6 показано поле зрения отсчётного микроскопа 15. В левом окне наблюдаются изображения диаметрально противоположных участков лимба и вертикальный штрих для отсчёта градусов, в правом – деления шкалы оптического микрометра и горизонтальная риска для отсчёта минут и секунд. Зрительная труба укреплена на подвижном кронштейне, который можно поворачивать вокруг вертикальной оси, проходящей через центр предметного столика. Поворот трубы осуществляется от руки после освобождения стопорного винта 24. При закрепленном винте 24 можно производить тонкое перемещение трубы с помощью винта 25. Вращение столика вместе с лимбом относительно алидады производится либо от руки при свободном винте 26, либо микрометрическим винтом 28 при зажатом винте 26. 2 Алидада (араб.) – вращающаяся линейка, служит для отсчета углов 67 Рис. 5.Внешний вид гониометра. Рис. 6. 68 Столик вращается относительно алидады и лимба либо от руки при свободном винте 27, либо точно микрометрическим винтом 29 при зажатом винте 27 (рычажок 20 в верхнем положении). Отсчет углов производится с помощью окуляра 15. При измерении используется только верхняя шкала, по которой перемещается подвижная риска (рис. 6). Цена деления шкалы 20 угловых минут. Резкость изображения шкалы регулируется вращением оправы окуляра 15. Измерение длин волн спектральных линий. Дифракционная решётка с известным периодом может быть использована для измерения длин волн, например, в спектре ртути. Как следует из (3), измерения длины волны сводятся к определению φm – угла отклонения лучей от первоначального направления. Проведя измерения дифракционных углов для спектра с известными длинами волн, можно решить обратную задачу – рассчитать период решётки. Определение угловой дисперсии. Для определения угловой дисперсии дифракционной решётки (см. формулу(4)) нужно измерить угловое расстояние ∆φ между двумя близкими спектральными линиями с длинами волн λ1 и λ2 и провести вычисления по формуле D = ∆φ/(λ1 – λ2). Оценка разрешающей способности решётки. Непосредственное экспериментальное определение разрешающей способности дифракционной решётки требует специальных источников света, в спектре которых имеются близкие спектральные линии, находящиеся на пределе разрешения. Обозначим через δλ разность их длин волн. Разрешающая сила определяется отношением λ/δλ. При сравнении результатов с теоретической величиной разрешающей силы (R = mN) необходимо принимать во внимание два обстоятельства. 1. При экспериментальной оценке разрешающей способности ширину щели коллиматора нужно выбирать достаточно малой. Полезно производить измерения при разных размерах щели, постепенно её уменьшая. Видимая ширина линии должна при этом сначала уменьшаться вместе с шириной щели, а затем оставаться постоянной. 2. Описанный метод позволяет измерить так называемую аппаратную или приборную разрешающую силу в реальных условиях опыта (т.е. для данной решётки, заданных размерах входной щели коллиматора, данном увеличении зрительной трубы и т.д.). Сравнение полученного результата с теоретическим (предельным) значением разрешающей силы позволяет оценить качество спектральной установки. Порядок выполнения работы 1. Включить ртутную лампу. 2. Произвести настройку гониометра так, чтобы щель и визирный крест были видны чётко. 69 3. Установить решётку на столике гониометра так, чтобы её плоскость была перпендикулярна оси коллиматора, перпендикулярна одному из винтов 8 и параллельна другому. 4. Установив начальное положение трубы (против коллиматора) на 0 180 и вращая только верхнюю часть столика (винт 26 закреплён), найти ахроматическое (белое) изображение щели коллиматора. 5. Винтом 8, перпендикулярным плоскости решётки, установить короткое изображение щели на центр поля зрения. Отводя алидаду в сторону от коллиматора, найти в трубе спектр самого дальнего порядка и вторым винтом 8 (параллельным плоскости решётки) снова привести изображение щели к центру. Вернуться к ахроматическому изображению щели поля зрения и проверить результат. При необходимости снова подстроить столик винтом, перпендикулярным плоскости решётки. Повторяя процедуру, методом последовательных приближений добиться того, чтобы при повороте трубы изображение щели и спектр уходили не больше, чем на треть радиуса поля зрения. 6. Закончив настройку, подобрать ширину входной щели так, чтобы хорошо разрешались линии жёлтого дублета (ширина изображения щели чуть больше промежутка между линиями двойного штриха окуляра). 7. Измерить угловые координаты спектральных линий ртути в одном из порядков. Спектр ртутной лампы приведён на рис. 7 и в таблице даны его характеристики. Визуально наблюдаться могут не все линии. Рис. 7. Спектр ртутной лампы ДРШ – 250 Таблица. 8. При выполнении измерений плоскость решётки остаётся перпендикулярной оси коллиматора, а зрительная труба поворачивается так, 70 чтобы отсчётный крест окуляра гониометра был совмещён с исследуемой спектральной линией. 9. Перед началом измерений следует убедиться в справедливости формулы (3). Для этого определить углы дифракции для одной из ярких линий спектра в разных порядках и убедиться, что sinφm ~ m. 10. При измерениях отмечайте угловую координату каждой из линий. Если при перемещении по спектру заметно нарушается резкость изображения, подстройте объектив зрительной трубы винтом 11. 11. Для оценки дисперсии решётки определить угловые координаты линий жёлтого дублета во всех видимых порядках. 12. Для оценки разрешающей способности измерьте угловую ширину одной из линий жёлтого дублета, предварительно установив минимально возможную ширину входной щели. Если точное измерение ширины отдельной линии затруднено, оцените на глаз, во сколько раз расстояние между линиями дублета больше полуширины одной линии, и рассчитайте аппаратную полуширину линии δλ. Обработка результатов 1. Для выбранного порядка m рассчитать углы дифракции φm и построить график зависимости sin φm от длины волны. Определить по углу наклона графика период решётки d, используя формулу (3). Оценить погрешность результата. 2. Рассчитать угловую дисперсию по формуле (4) для жёлтого дублета в спектрах разных порядков (в угловых секундах на ангстрем). Сравнить результаты между собой и с теоретическим значением, рассчитанным по формуле (6). 3. Оценить экспериментальную разрешающую способность. Пользуясь формулой (10), оценить размер освещённой части решётки. Контрольные вопросы 2. Дайте определения спектральных характеристик дифракционной решётки. 3. Сформулируйте критерий разрешения Рэлея. 4. Какова роль коллиматора, расположенного за дифракционной решёткой? 5. Почему ширина спектра увеличивается, а интенсивность света падает с ростом порядка спектра? 6. Что называется разрешающей способностью дифракционной решётки? 7. Почему растёт разрешающая способность с ростом числа щелей? 8. На дифракционную решётку с постоянной равной 6,5 мкм падает нормально монохроматический свет с длиной волны 0,65 мкм. Определить общее число главных максимумов, поучаемых с помощью этой решётки. 71 Литература 1. Савельев И.В. Курс общей физики. Спб.: Лань, 2008, кн. 4, §5.5 – 5.6. 2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Академия, 2007, §32.3 – 31.3. 3. Трофимова Т.И. Курс физики. М.: Академия, 2008, §180. 4. Кингсеп А.С., Локшин Г.Р., Ольхов О.А. Основы физики – Т. I. Механика, электричество и магнетизм, колебания и волны, волновая оптика. – М.: ФИЗМАТЛИТ, 2001. Ч.III, Гл. 8, §8.8 – 8.9. Работа № 8 ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИФРАКЦИОННОЙ РЕШЁТКИ С ПОМОЩЬЮ ГОНИОМЕТРА Цель работы Знакомство с работой гониометра и определение спектральных характеристик дифракционной решётки. Приборы и принадлежности Дифракционная решётка, ртутная разрядная лампа высокого давления ДРШ – 250 с блоком питания, гониометр. Теоретическая часть Дифракция представляет собой совокупность явлений, наблюдаемых при распространении волн в резко неоднородной среде (например, вблизи границ тела, при прохождении волн сквозь отверстия), когда размеры неоднородностей по величине сравнимы с длиной волны. В случае дифракции Френеля (сферические волны) дифракционная картина создается сходящимися лучами. При дифракции Фраунгофера (плоские волны) лучи распространяются параллельно, поэтому для наблюдения дифракционной картины, на их пути помещают собирающую линзу и устанавливают экран в её фокальной плоскости, как показано на рис. 1. Дифракционная решетка представляет собой строго периодическую структуру, состоящую из N одинаковых щелей шириной b в непрозрачном экране, отстоящих друг от друга на одно и то же расстояние a. Величина d = а b называется периодом решетки (рис. 1). 72 Как правило, дифракционной решёткой служит стеклянная или металлическая пластина, на которую с помощью делительной машины через строго одинаковые интервалы нанесены параллельные штрихи. В учебных лабораториях применяются отпечатки таких гравированных решёток – так называемые реплики, изготовленные из специальной пластмассы. Обычно дифракционная решётка освещается плоской волной, распространяющейся перпендикулярно её поверхности (рис. 1), а плоскость наблюдения практически находится в бесконечности (условия дифракции Фраунгофера). В этом случае направление, в котором производится наблюдение, определяется углом φ между нормалью к решётке и направлением лучей. А распределение интенсивности света, наблюдаемое при дифракции Фраунгофера на решетке, представляет собой интерференционно-дифракционную картину, возникающую как результат суммарной многолучевой интерференции дифракционной картины на каждой щели от всех N щелей. 73 Каждая щель дифракционной решетки в отдельности, для монохроматической волны, дает дифракционную картину, представленную на рис.2. На рисунке изображена зависимость интенсивности волны Iφ от синуса угла , т.е. отклонения волнового вектора от нормали, как показано на Рис. 2. Распределение интенсивности Iφ при дифракции света на одной щели. рис.1. Иными словами, если бы мы закрыли все щели на дифракционной решетке, оставив только одну из них, и поместили экран в фокальную плоскость (как показано на Рис.1), то мы увидели бы напротив этой щели картинку с распределением интенсивности света, как показано на рис.2. Аналитическое выражение для распределения интенсивности в дифракционной картине от одной щели может быть получено на основании принципа Гюйгенса-Френеля, учитывающего интерференцию зон Френеля плоской волны. Эта функция, график которой представлен на рис. 2, равна 74 Iφ = I0 ﴾ 𝜋𝑏 sin 𝑢 2 𝑢 ﴿ (1) где u = sin 𝜑, и характеризует распределение интенсивности в результате 𝜆 дифракции плоской волны на каждой щели. Анализируя выражение (1) на предмет экстремумов, заметим, что при u 0 предел lim sin u =1. Но при u 0 u также и sin 0, а значит и 0 и, следовательно, интенсивность при = 0 равна Iφ = I0. Обратим внимание на тот факт, что условие этого максимума не зависит от длины волны , а, значит, будет справедливо для всех длин волн. Этот максимум интенсивности света соответствует центральному участку спектра, расположенному на пересечении главной оптической оси линзы с ее фокальной плоскостью, независимо от положения щели (точка F на рис. 1). Действительно, условие = 0 означает, что луч перпендикулярен плоскости дифракционной решетки, а, значит, параллелен главной оптической оси линзы. Но точно такое же рассмотрение мы можем провести для каждой щели. Следовательно, лучи от каждой щели, распространяющиеся под углом = 0, соберутся в фокусе линзы, как параллельный пучок света, вне зависимости от их длины волны, и цвет полосы будет белым. Теперь зададимся вопросом: где будут расположены минимумы функции (1)? Очевидно, что нули функции Iφ являются минимумами (поскольку ноль всегда является минимумом квадратичной функции) и совпадают с нулями функции sin u=0 (u=πk, k = ±1; ±2, …; k ≠ 0), при u 0 (иначе (1) теряет 𝜋𝑏 смысл). Принимая во внимание, что u = sin 𝜑, получаем условия для 𝜆 минимумов функции (1) u=πk : bsin 𝜑 = kλ, где – λ длина падающей световой волны. Обратим внимание на тот факт, что условие для минимумов функции Iφ оказывается уже зависимым от длины волны. Таким образом, положение минимумов функции Iφ на экране будет различным для различных длин волн. Несложно сообразить, что между двумя последовательными минимумами должен находиться максимум. Точное положение максимумов можно определить, продифференцировав (1) по и приравняв нулю производную. Теперь мысленно откроем все остальные щели дифракционной решетки. Интенсивность света Iφ, распространяющегося после дифракции на решётке под углом дифракции φ к нормали решетки, состоящей из N щелей, в произвольной точке Р (рис. 1), описывается выражением, которое учитывает как интерференцию волн, приходящих от разных щелей, так и дифракцию на каждой щели: Iφ = I0 ﴾ 𝜋𝑑 sin 𝑢 2 sin 𝑁𝛿 2 𝑢 ﴿ ﴾ sin 𝛿 ﴿ , (2) где δ = sin 𝜑. Множитель I0 определяет величину потока энергии, 𝜆 излучаемого в направлении 𝜑 = 0, т.е. потока энергии недифрагировавшего света. Множитель ﴾ sin 𝑢 2 𝑢 ﴿ , как мы убедились выше, характеризует 75 распределение интенсивности в результате дифракции плоской волны на sin 𝑁𝛿 2 каждой отдельной щели, а множитель ﴾ ﴿ в формуле учитывает sin 𝛿 интерференцию между пучками, исходящими из всех щелей. График первого сомножителя функции (2) от аргумента sin 𝜑 представлен на рис. 3б (он совпадает с графиком, представленным на рис. 2). Теперь проанализируем поведение интерференционного (второй сомножитель) члена в формуле (2). Как следует из рис. 1, разность хода от соседних щелей равна ∆ = dsinφ (где d период решетки), а интенсивность дифрагированного света максимальна для тех углов φm , для которых волны, собираемые линзой в точке наблюдения от всех щелей решётки, оказываются в фазе. Для всех направлений справедливо интерференционное соотношение: dsinφm = ±mλ (m = 0,1,2,…), (3) где число m даёт порядок главного максимума. Максимум нулевого порядка один, и мы уже обсудили выше, что все лучи с =0 соберутся в центральном максимуме. Все остальные интерференционные максимумы расположены симметрично относительно нулевого (центрального) максимума c левой и правой стороны. Во всех интерференционных максимумах, определяемых условием (3), колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда волны в максимуме возрастает в N раз: А м ак. = NА0, где А0 – амплитуда волны, прошедшей через одну щель. Интенсивность волны I ~ A 2 и, следовательно, I м ак. = N2 I0. Этот результат является следствием интерференции когерентных волн (N некогерентных источников дают интенсивность I м ак. = N I0). Тот же результат можно получить более строго, если с помощью правила Лопиталя посчитать предел sin 𝑁𝛿 2 при sin 0 функции lim ﴾ ﴿ = 𝑁 2 . Но поскольку функция sin sin 𝛿 является периодической, то количество главных интерференционных максимумов будет велико. Побочные интерференционные максимумы могут быть установлены путем дифференцирования по . График функции 1 sin 𝑁𝛿 2 ﴿ представлен на рис. 3а. Из сопоставления рисунков 3а и 3б несложно увидеть, что интерференционные максимумы гораздо уже, чем дифракционные. Действи𝑁2 ﴾ sin 𝛿 76 Рис . 3. Распреде ление интенсив ностей (I/I0) при дифракции света на правильной структуре из N щелей: а) распределение интенсивности, обусловленное интерференцией пучков от разных щелей; б) Распределение интенсивности, обусловленное дифракцией на каждой щели; в) суммарное распределение. тельно, угловая ширина центрального максимума в Nd/b N раз меньше, чем при дифракции на одной щели, что следует из формулы (2). Чтобы получить график функции (2), необходимо перемножить графики 3а и 3б. На рис. 3в представлено суммарное распределение Iφ. Таким образом, максимумы интенсивности дифракционной решетки зависят от числа щелей: Imax = N2Iφ а дифракционная картина выражена тем резче, чем больше число щелей N. Как следует из (3), положение всех главных интерференционных максимумов, кроме нулевого, зависит от длины волны. Поэтому главные максимумы различных длин волн будут разделены на экране; таким образом, дифракционная решетка будет производить разложение немонохроматического излучения на спектральные составляющие, причём фиолетовые лучи будут отклоняются решёткой меньше, чем красные. Входящая в (3) величина m носит название порядка спектра. При m = 0 максимумы интенсивности для всех длин волн располагаются при φ = 0 и накладываются друг на друга. При освещении белым светом нулевой максимум, в отличие от всех прочих, поэтому оказывается неокрашенным. Спектры первого, второго и т.д. порядков располагаются симметрично по обе стороны от нулевого. Основными характеристиками любого спектрального прибора являются дисперсия и разрешающая сила. Угловая дисперсия. Дисперсия D характеризует угловое расстояние между близкими спектральными линиями: 77 𝑑𝜑 D = . 𝑑𝜆 Беря дифференциалы от обеих частей (3), получим: dcosφdφ = m∙dλ. Следовательно, 𝑑𝜑 𝑚 𝑚 D= = = 2 2 2. 𝑑𝜆 𝑑 cos 𝜑 (4) (5) (6) √𝑑 −𝑚 𝜆 Дисперсия возрастает с увеличением порядка спектра. На опыте дисперсию решётки определяют путём измерения углового расстояния ∆φ между двумя близкими спектральными линиями с известной разностью длин волн ∆λ (например, между двумя жёлтыми линиями ртути). Разрешающая способность дифракционной решётки. Возможность разрешения двух близких спектральных линий зависит от их ширины3 и от расстояния между ними. Пусть в спектре m-го порядка наблюдаются две близкие спектральные линии с длинами волн λ и λ + ∆λ. Угловое расстояние ∆φ между этими линиями, согласно (5), равно 𝑚∆𝜆 ∆φ = (7) 𝑑 cos 𝜑 Согласно критерию разрешения Релея два дифракционных максимума воспринимаются раздельно, если середина одного максимума совпадает с краем (минимумом) другого (рис. 4). Такому взаимному расположению разрешаемых максимумов одинаковой интенсивности соответствует пересечение их распределений на уровне половины от максимального значения (рис. 4). Как следует из (2), при переходе из главного максимума (φ = 0) в минимум величина N(kd sinφ)/2 изменяется на π, так что 𝑁𝑘𝑑 2 [sin(φ+dφ) – sin φ] = π, (8) Рис.4. К определению разрешающей способности дифракционной решётки. где dφ – угловая полуширина главного максимума. Принимая во внимание малость dφ, получим из (8) dφ = 𝜆 𝑁𝑑 cos 𝜑 . (9) Отметим, что угловая полуширина максимума обратно пропорциональна Здесь и далее – ширина изображения спектральной линии, определяемая дифракцией, а не её собственная ширина. 3 78 видимому размеру решётки – 𝑁𝑑 cos 𝜑. По определению, разрешающая способность спектрального прибора R = λ/δλ – это отношение длины волны к разности длин волн двух линий, разрешаемых по критерию Релея. Приравнивая δφ (9) и ∆φ (7) для случая предельного разрешения, найдём для дифракционной решётки R= 𝜆 𝛿𝜆 = m∙N . (10) Спектральный интервал δλ, входящий в соотношение (10), характеризует минимальное расстояние между двумя спектральными линиями, которые ещё могут быть разрешены при помощи данной дифракционной решётки. Экспериментальная установка. При работе с дифракционной решёткой основной задачей является точное измерение углов, при которых наблюдаются главные максимумы для различных длин волн. В данной работе для измерения углов используется гониометр Г5, внешний вид которого показан на рис. 5. Коллиматор 3, столик 7 и алидада4 17 со зрительной трубой 12 крепятся на массивном основании 23. На столике 7 размещаются исследуемые объекты. Коллиматор закреплён неподвижно, а столик и алидада с трубой могут вращаться вокруг вертикальной оси. На рис. 6 показано поле зрения отсчётного микроскопа 15. В левом окне наблюдаются изображения диаметрально противоположных участков лимба и вертикальный штрих для отсчёта градусов, в правом – деления шкалы оптического микрометра и горизонтальная риска для отсчёта минут и секунд. Зрительная труба укреплена на подвижном кронштейне, который можно поворачивать вокруг вертикальной оси, проходящей через центр предметного столика. Поворот трубы осуществляется от руки после освобождения стопорного винта 24. При закрепленном винте 24 можно производить тонкое перемещение трубы с помощью винта 25. Вращение столика вместе с лимбом относительно алидады производится либо от руки при свободном винте 26, либо микрометрическим винтом 28 при зажатом винте 26. 4 Алидада (араб.) – вращающаяся линейка, служит для отсчета углов 79 Рис. 5.Внешний вид гониометра. Рис. 6. 80 Столик вращается относительно алидады и лимба либо от руки при свободном винте 27, либо точно микрометрическим винтом 29 при зажатом винте 27 (рычажок 20 в верхнем положении). Отсчет углов производится с помощью окуляра 15. При измерении используется только верхняя шкала, по которой перемещается подвижная риска (рис. 6). Цена деления шкалы 20 угловых минут. Резкость изображения шкалы регулируется вращением оправы окуляра 15. Измерение длин волн спектральных линий. Дифракционная решётка с известным периодом может быть использована для измерения длин волн, например, в спектре ртути. Как следует из (3), измерения длины волны сводятся к определению φm – угла отклонения лучей от первоначального направления. Проведя измерения дифракционных углов для спектра с известными длинами волн, можно решить обратную задачу – рассчитать период решётки. Определение угловой дисперсии. Для определения угловой дисперсии дифракционной решётки (см. формулу(4)) нужно измерить угловое расстояние ∆φ между двумя близкими спектральными линиями с длинами волн λ1 и λ2 и провести вычисления по формуле D = ∆φ/(λ1 – λ2). Оценка разрешающей способности решётки. Непосредственное экспериментальное определение разрешающей способности дифракционной решётки требует специальных источников света, в спектре которых имеются близкие спектральные линии, находящиеся на пределе разрешения. Обозначим через δλ разность их длин волн. Разрешающая сила определяется отношением λ/δλ. При сравнении результатов с теоретической величиной разрешающей силы (R = mN) необходимо принимать во внимание два обстоятельства. 3. При экспериментальной оценке разрешающей способности ширину щели коллиматора нужно выбирать достаточно малой. Полезно производить измерения при разных размерах щели, постепенно её уменьшая. Видимая ширина линии должна при этом сначала уменьшаться вместе с шириной щели, а затем оставаться постоянной. 4. Описанный метод позволяет измерить так называемую аппаратную или приборную разрешающую силу в реальных условиях опыта (т.е. для данной решётки, заданных размерах входной щели коллиматора, данном увеличении зрительной трубы и т.д.). Сравнение полученного результата с теоретическим (предельным) значением разрешающей силы позволяет оценить качество спектральной установки. Порядок выполнения работы 13.Включить ртутную лампу. 14. Произвести настройку гониометра так, чтобы щель и визирный крест были видны чётко. 81 15. Установить решётку на столике гониометра так, чтобы её плоскость была перпендикулярна оси коллиматора, перпендикулярна одному из винтов 8 и параллельна другому. 16. Установив начальное положение трубы (против коллиматора) на 0 180 и вращая только верхнюю часть столика (винт 26 закреплён), найти ахроматическое (белое) изображение щели коллиматора. 17. Винтом 8, перпендикулярным плоскости решётки, установить короткое изображение щели на центр поля зрения. Отводя алидаду в сторону от коллиматора, найти в трубе спектр самого дальнего порядка и вторым винтом 8 (параллельным плоскости решётки) снова привести изображение щели к центру. Вернуться к ахроматическому изображению щели поля зрения и проверить результат. При необходимости снова подстроить столик винтом, перпендикулярным плоскости решётки. Повторяя процедуру, методом последовательных приближений добиться того, чтобы при повороте трубы изображение щели и спектр уходили не больше, чем на треть радиуса поля зрения. 18. Закончив настройку, подобрать ширину входной щели так, чтобы хорошо разрешались линии жёлтого дублета (ширина изображения щели чуть больше промежутка между линиями двойного штриха окуляра). 19. Измерить угловые координаты спектральных линий ртути в одном из порядков. Спектр ртутной лампы приведён на рис. 7 и в таблице даны его характеристики. Визуально наблюдаться могут не все линии. Рис. 7. Спектр ртутной лампы ДРШ – 250 Таблица. 20. При выполнении измерений плоскость решётки остаётся перпендикулярной оси коллиматора, а зрительная труба поворачивается так, 82 чтобы отсчётный крест окуляра гониометра был совмещён с исследуемой спектральной линией. 21. Перед началом измерений следует убедиться в справедливости формулы (3). Для этого определить углы дифракции для одной из ярких линий спектра в разных порядках и убедиться, что sinφm ~ m. 22. При измерениях отмечайте угловую координату каждой из линий. Если при перемещении по спектру заметно нарушается резкость изображения, подстройте объектив зрительной трубы винтом 11. 23. Для оценки дисперсии решётки определить угловые координаты линий жёлтого дублета во всех видимых порядках. 24. Для оценки разрешающей способности измерьте угловую ширину одной из линий жёлтого дублета, предварительно установив минимально возможную ширину входной щели. Если точное измерение ширины отдельной линии затруднено, оцените на глаз, во сколько раз расстояние между линиями дублета больше полуширины одной линии, и рассчитайте аппаратную полуширину линии δλ. Обработка результатов 4. Для выбранного порядка m рассчитать углы дифракции φm и построить график зависимости sin φm от длины волны. Определить по углу наклона графика период решётки d, используя формулу (3). Оценить погрешность результата. 5. Рассчитать угловую дисперсию по формуле (4) для жёлтого дублета в спектрах разных порядков (в угловых секундах на ангстрем). Сравнить результаты между собой и с теоретическим значением, рассчитанным по формуле (6). 6. Оценить экспериментальную разрешающую способность. Пользуясь формулой (10), оценить размер освещённой части решётки. Контрольные вопросы 9. Дайте определения спектральных характеристик дифракционной решётки. 10. Сформулируйте критерий разрешения Рэлея. 11. Какова роль коллиматора, расположенного за дифракционной решёткой? 12. Почему ширина спектра увеличивается, а интенсивность света падает с ростом порядка спектра? 13. Что называется разрешающей способностью дифракционной решётки? 14. Почему растёт разрешающая способность с ростом числа щелей? 15. На дифракционную решётку с постоянной равной 6,5 мкм падает нормально монохроматический свет с длиной волны 0,65 мкм. Определить общее число главных максимумов, поучаемых с помощью этой решётки. 83 Литература 1. Савельев И.В. Курс общей физики. Спб.: Лань, 2008, кн. 4, §5.5 – 5.6. 2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Академия, 2007, §32.3 – 31.3. 3. Трофимова Т.И. Курс физики. М.: Академия, 2008, §180. 4. Кингсеп А.С., Локшин Г.Р., Ольхов О.А. Основы физики – Т. I. Механика, электричество и магнетизм, колебания и волны, волновая оптика. – М.: ФИЗМАТЛИТ, 2001. Ч.III, Гл. 8, §8.8 – 8.9. Содержание Работа № 1. Определение главных фокусных расстояний собирающей и рассеивающей линз ………………………………………………………… 3 Работа № 2. Определение радиуса кривизны линзы интерференционным методом ……………………………………………………………………. 16 Работа № 3. Определение периода дифракционной решетки при помощи HeNe лазера. …………………………………………………….…………………22 Работа № 4. Изучение закона освещённости с помощью фотоэлемента..29 Работа № 5. Изучение поляризованного света. Закон Малюса……………34 Работа № 6. Изучение спектра излучения неоновой лампы с помощью монохроматора ……………………………………………………..…………41 Работа № 7. Определение основных характеристик призмы с помощью гониометра……………………………………………………………………. 49 Работа № 8. Определение основных характеристик дифракционной решётки с помощью гониометра ……………………………………………………….61 84