Ответ: 13 м

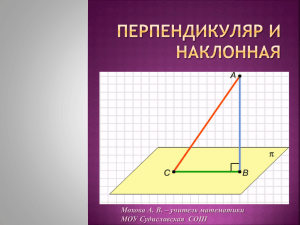
Геометрия 8 класс к учебнику Погорелова
У ро к №
Д ата про веде ния ур ок а
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Ц ел и:
-дать определения проекции, наклонной;
-научить решать задачи по данным определениям;
-содействовать рациональной организации труда учащихся.
Хо д у ро ка
I. Актуализация опорных знаний.
Математический диктант
I вариант
1.
Найдите
длину
II вариант
гипотенузы 1.
Найдите
длину
катета
прямоугольного треугольника, если прямоугольного треугольника, если
его катеты равны 5 и 12 м.
другой катет и гипотенуза равны
соответственно 40 и 41 см.
Ответ: 13 м
Ответ: 9 см
2. Запишите теорему Пифагора для 2. Запишите теорему Пифагора для
ABC , у которого A  прямой.
ABC , у которого B  прямой.
Ответ: BC 2  AC 2  AB 2
Ответ: AC 2  AB 2  BC 2
3.
Найдите
длину
катета 3. Найдите длину гипотенузы
прямоугольного треугольника, если прямоугольного треугольника, если
другой катет и гипотенуза равны катеты равны 6 и 8 мм.
соответственно 60 и 61 дм.
Ответ: 11 дм
Ответ: 10 мм
1
Геометрия 8 класс к учебнику Погорелова
II. Формирование новых понятий.
BA  a ; точка С - любая точка прямой а, отличная от
B
точки А.
ВС называется наклонной, проведенной из точки В к
a
C
A
прямой а. Точка С называется основанием наклонной,
отрезок АС называется проекцией наклонной.
По заданному чертежу назвать:
M
1) наклонные к прямой и их
основания;
2)
перпендикуляр
и
его
основание;
a
F
3) проекцию каждой наклонной.
K
R
P
Устные задачи:
Из одной точки к прямой проведены перпендикуляр и наклонная.
1) Длина наклонной 10 см, а перпендикуляра 6 см. Чему равна проекция
наклонной? (8 см)
2) Наклонная длиной 13 см имеет проекцию 12 см. Вычислите длину
перпендикуляра. (5 см)
Следствие 1. Если к прямой из одной точки проведены перпендикуляр и
наклонная, то наклонная больше перпендикуляра.
Для доказательства достаточно указать, что перпендикуляр - это катет, а
наклонная - гипотенуза.
Следствие 2. Если к прямой из одной точки проведены перпендикуляр и
наклонные, то равные наклонные имеют равные проекции.
2
Геометрия 8 класс к учебнику Погорелова
C
Доказательство. В прямоугольных
треугольниках MNF и MKR по теореме
Пифагора из MKF : FK 2  MF 2  MK 2 ,
l
из MKR : KR 2  MR 2  MK 2 , а так как
MF  MR ,
то FK  KR.
A
l
h
D
B
Следствие 3. Если к прямой из одной точки проведены две наклонные, то
больше из них та, у которой проекция больше.
III. Формирование умений и навыков.
№21.
Решение.
Отложим от точки D на прямой a отрезки AD и DB, равные l 2  h 2 .
AC 
CB  l
l
2
 h2
 h
2
2
 l 2  h 2  h 2  l 2  l.
(по теореме Пифагора); по свойству наклонных третьей
наклонной не может быть.
№16.
C
Решение.
BO  CD,
ABOD  прямоуголь ник ,
AB  DO  4 м,
B
AD  BO  10 м,
CO  CD  OD  8  4  4( м).
BOC  прямоуголь ный 
O 8м
4м
BC  BO 2  CO 2  10 2  4 2  116  10,8( м).
A
Ответ: длина желоба 10,8 м.
IV. Итог урока.
Домашнее задание: п. 65, вопросы 5-6, №17, 20.
3
10 м
D