Билеты для экзамена 2013x

Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 13
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Прогнозирование по регрессионной модели в рамках классической линейной регрессии и его точность.
Доверительный интервал для прогнозных значений.
2.
Функциональные преобразования при построении кривых Филлипса и Энгеля.
3.
Понятие об автокорреляции случайной составляющей. Экономические причины автокорреляции.
Последствия игнорирования автокорреляции для свойств оценок коэффициентов регрессии, полученных методом
наименьших квадратов. Графическое диагностирование автокорреляции.
4.
Линейная регрессия в случае стохастических регрессоров. Теория перманентного дохода Фридмена.
Обобщение теоремы Гаусса-Маркова на случай стохастических регрессоров (без доказательства).
5.
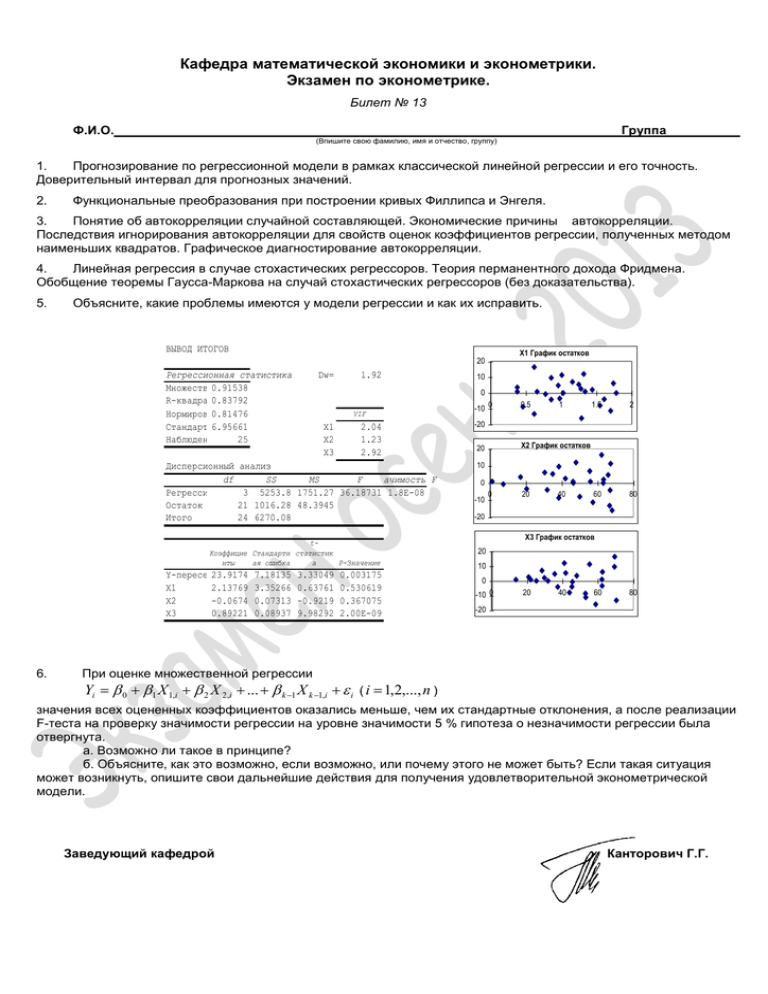
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
0
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
10
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
-10 0
0.5
1
1.5
2
60
80
-20
X2 График остатков
20
10
0
-10
0
20
40
-20
X3 График остатков
20
10
0
-10 0
20
40
60
80
-20
При оценке множественной регрессии
Yi   0  1 X 1,i   2 X 2,i  ...   k 1 X k 1,i   i ( i  1,2,..., n )
значения всех оцененных коэффициентов оказались меньше, чем их стандартные отклонения, а после реализации
F-теста на проверку значимости регрессии на уровне значимости 5 % гипотеза о незначимости регрессии была
отвергнута.
а. Возможно ли такое в принципе?
б. Объясните, как это возможно, если возможно, или почему этого не может быть? Если такая ситуация
может возникнуть, опишите свои дальнейшие действия для получения удовлетворительной эконометрической
модели.
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 16
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Множественная линейная регрессия в скалярной и векторной формах. Матричное выражение для вектора
оценок коэффициентов регрессии их диперсионно-ковариационной матрицы.
2.
Анализ сезонности с помощью фиктивных переменных.
3.
Преобразование исходных переменных, позволяющее применить метод наименьших квадратов при наличии
автокорреляции. Метод поиска на сетке Хилдрет-Лю (Hildreth-Lu grid search procedure).
4.
Несостоятельность оценок МНК при нарушении условия предопределенности. Метод инструментальных
переменных (instrumental variables, IV).
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
VIF
X1
X2
X3
12.04
9.23
1.22
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
6.
7.18135
3.35266
0.07313
0.08937
10
0
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
X1 График остатков
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
-10 0
0.5
1
1.5
2
-20
15
10
5
0
-5 0
-10
-15
15
10
5
0
-5 0
-10
-15
X2 График остатков
20
40
60
80
60
80
X3 График остатков
20
40
Необходимо оценить параметры регрессии
Yi    X i  ui .
Есть основания полагать, что дисперсия случайного остатка зависит от некоторого фактора Z. Объясните, каким
образом Вы выберете один из следующих видов этой зависимости для получения эффективных оценок
коэффициентов регрессии:
а.
Var (ui )   2 ;
б.
Var (ui )   2 Z i ;
в.
Var (ui )   2 Z i2 ;
г.
Var (ui )   2 Z i3 .
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 38
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Проверка значимости коэффициентов и адекватности регрессии для множественной линейной
регрессионной модели.
2.
Формулировка общей линейной гипотезы (наличия нескольких линейных соотношений между параметрами
теоретической регрессии) и ее проверка.
3.
Нарушение гипотезы о гомоскедастичности. Тест Голдфелда-Квандта (Goldfeld-Quandt)
4.
Метод максимального правдоподобия. Свойства оценок метода максимального правдоподобия.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
0.38
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.187313 1.76029E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.0031753
0.5306194
0.3670751
2.00E-09
X1 График остатков
10
0
-10 0
0.5
1
1.5
2
60
80
60
80
-20
15
10
5
0
-5 0
-10
-15
15
10
5
0
-5 0
-10
-15
X2 График остатков
20
40
X3 График остатков
20
40
6.
Заданы две регрессии с двумя объясняющими переменными, оцененные на разных выборках. Объясните,
как может получиться, что в одном случае при корреляции между двумя факторами, равной 0.8, необходимо
принимать меры против мультиколлинеарности, а в другом случае при корреляции между теми же двумя
факторами, равной 0.9, такой необходимости не возникает.
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 14
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии
и его следствия. Проверка нормальности случайной ошибки.
2.
Мультиколлинеарность данных. Теоретические последствия мультиколлинеарности для оценок параметров
регрессионной модели. Признаки наличия и показатели степени мультиколлинеарности.
3.
Преобразование исходных переменных, позволяющее применить метод наименьших квадратов при
наличии автокорреляции. Двух-шаговая процедура Кокрена-Оркутта. Двух шаговая процедура Дарбина.
4.
Модели панельных данных. Модель с фиксированными эффектами. Модель со случайными эффектами.
Тест Хаусмана.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.18731 1.76029E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
5.
6.
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
X1 График остатков
10
0
-10 0
0.5
1
1.5
2
60
80
-20
20
X2 График остатков
10
0
-10 0
20
40
-20
20
X3 График остатков
10
0
-10 0
20
40
60
80
-20
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
В Вашем распоряжении – выборки
{xi } и { yi } одинакового размера. Объясните, каким образом с помощью
МНК Вы будете оценивать параметры  и  следующих функциональных зависимостей? Какие предположения
следует сделать относительно распределения случайного члена в каждой из оцениваемых Вами моделей для того,
чтобы сохранялась возможность проверять различные гипотезы относительно коэффициентов, пользуясь
стандартными таблицами распределений?
y
exp(  x)
1  exp(  x)
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 23
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Ковариационная матрица оценок коэффициентов регрессии. Несмещенная оценка дисперсии случайного
члена (без доказательства). Оценка ковариационной матрицы оценок коэффициентов регрессии.
2.
Построение множественной линейной регрессии с ограничениями на параметры (рассмотрение конкретных
примеров без вывода общей формулы).
3.
Оценка неизвестных дисперсий по результатам тестов Парка и Глейзера в условиях гетероскедастичности.
4.
Модель с распределенными лагами. Преобразование Койка (Koyck). Авторегрессионные модели, как
эквивалентное представление моделей с распределенными лагами.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
X1 График остатков
20
Dw=
2.05
0
X1
X2
X3
12.04
9.23
1.22
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
7.18135
3.35266
0.07313
0.08937
0
VIF
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
1
2
-20
X2 График остатков
20
10
0
-10 0
20
40
60
80
60
80
-20
X3 График остатков
20
10
0
-10
0
20
40
-20
6.
Проверьте, если это возможно, гипотезу об отсутствии автокорреляции в приведенных ниже уравнениях, а
если невозможно – объясните, почему. (в скобках приведены значения стандартных отклонений, n – число
измерений, DW – значение статистики Дарбина-Уотсона):
(n=35, DW = 1.81).
Yˆ  7.40 X 1  1.11 X 2
( 3.22)
( 0.057)
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 17
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Метод наименьших квадратов (МНК). Свойства оценок параметров, полученных по МНК.
2.
Использование качественных объясняющих переменных. Фиктивные (dummy) переменные в множественной
линейной регрессии. Влияние выбора базовой категории на интерпретацию коэффициентов регрессии.
3.
Регрессионные динамические модели. Лаговые переменные и экономические зависимости между
разновременными значениями переменных. Модель с распределенными лагами. Подход Тинбергена и Альта
(Tinbergen and Alt) к оценке моделей с распределенными лагами.
4.
Модель частичной подстройки (partial adjustment). Модель корректировки ошибками (error correction model,
ECM).
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
VIF
X1
X2
X3
2.04
9.23
11.22
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.18731 1.76029E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
15
10
5
0
-5 0
-10
-15
X1 График остатков
0.5
1
1.5
2
X2 График остатков
15
10
5
0
-5 0
-10
-15
20
40
60
80
60
80
X3 График остатков
15
10
5
0
-5 0
-10
-15
20
40
Необходимо параметры регрессии:
Yi    1 X i1   2 X i 2   i
Есть основания предполагать, что дисперсия ошибок возрастает с увеличением X1. К каким последствиям это
может привести? Как проверить эту гипотезу?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 12
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Методология эконометрического исследования. Математическая и эконометрическая модель. Три типа
экономических данных: временные ряды, перекрестные (cross-section) данные, панельные данные. Задача
оценивания параметров.
2.
Линейная в логарифмах регрессия, как модель с постоянной эластичностью. Оценка производственной
функции Кобба-Дугласа.
3.
Взвешенный метод наименьших квадратов при известных дисперсиях случайных составляющих в различных
наблюдениях.
4.
Модель адаптивных (adaptive) ожиданий и преобразование Койка.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
VIF
X1
X2
X3
12.04
9.23
1.22
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
X1 График остатков
10
0
-10 0
0.5
1
1.5
2
-20
15
10
5
0
-5 0
-10
-15
15
10
5
0
-5 0
-10
-15
X2 График остатков
20
40
60
80
60
80
X3 График остатков
20
40
6.
Если модель содержит лаговые переменные, статистику Дарбина-Уотсона использовать нельзя. Каким
образом в этом случае можно проверить, есть ли автокорреляция?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 36
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Особенности регрессии, проходящей через начало координат (без свободного члена). Выражения для
вычисления коэффициента наклона и его дисперсии при отсутствии свободного члена.
2.
Полиномиальная регрессия.
3.
Обобщенный метод наименьших квадратов для оценки коэффициентов регрессии при наличии
автокорреляции и известном значении параметра ρ. Преобразование исходных переменных, позволяющее
применить метод наименьших квадратов при наличии автокорреляции и известном значении параметра ρ.
4.
Модели бинарного выбора. Модель линейной вероятности. Модели логит и пробит. Предельные эффекты.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
0
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.18731 1.76029E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
0
VIF
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
0.5
1
1.5
2
60
80
-20
X2 График остатков
20
10
0
-10 0
20
40
-20
X3 График остатков
20
0
0
20
40
60
80
-20
Были оценены параметры регрессии:
Yi  3.40 2.81 X i1  0.53 X i 2
(1.21)
( 3.60)
R 2  0.85
( 0.79)
Исследователь сделал вывод об отсутствии влияния регрессоров на объясняемую переменную и неадекватности
модели в целом. Прав ли он? Ответ обоснуйте. Если не прав, объясните, что нужно делать в такой ситуации.
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 33
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Теорема Гаусса-Маркова (с доказательством) в случае классической линейной регрессии с одной
объясняющей переменной.
2.
Фиктивные переменные для дифференциации коэффициентов наклона в множественной линейной
регрессии.
3.
Преобразование исходных переменных, позволяющее применить метод наименьших квадратов при наличии
автокорреляции. Итеративная процедура Кокрена-Оркутта (Cochrane-Orcutt).
4.
Понятие о коинтеграции временных рядов. Двухшаговая процедура Грэйнджера-Энгла по проверке
коинтеграции двух временных рядов.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
VIF
X1
X2
X3
2.04
1.23
2.92
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
6.
7.18135
3.35266
0.07313
0.08937
10
0
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.18731 1.76029E-08
21 1016.28 48.3945
24 6270.08
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
X1 График остатков
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
-10 0
0.5
1
1.5
2
60
80
-20
20
X2 График остатков
10
0
-10 0
20
40
-20
20
X3 График остатков
10
0
-10 0
20
40
60
80
-20
Оценивается следующая модель:
Yi    1 X i1   2 X i 2   3 X i 3   i
Есть сведения о высокой коррелированности X1 иX3. Достаточно ли этого для того, чтобы сделать вывод о
наличии мультиколлинеарности. Если да, то почему? Если нет, что необходимо сделать, чтобы проверить, есть ли
она?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 21
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Линейная регрессионная модель для случая одной объясняющей переменной. Теоретическая и выборочная
регрессии. Экономическая интерпретация случайной составляющей. Линейность регрессии по переменным и
параметрам.
2.
Функциональные преобразования переменных в линейной регрессионной модели.
3.
Оценивание коэффициентов множественной линейной регрессии в условиях гетероскедастичности при
неизвестных дисперсиях случайных составляющих (Feasable Generalized Least Squares). Оценка неизвестных
дисперсий по результатам тестов Парка и Глейзера.
4.
Ожидания (expectations) экономических агентов, как причина лаговых переменных в моделях. Модели
наивных (naive) ожиданий.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
VIF
X1
X2
X3
2.04
9.23
11.22
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
15
10
5
0
-5 0
-10
-15
X1 График остатков
0.5
1
1.5
2
X2 График остатков
15
10
5
0
-5 0
-10
-15
20
40
60
80
60
80
X3 График остатков
15
10
5
0
-5 0
-10
-15
20
40
6.
Необходимо проверить гипотезу о наличии автокорреляции в модели. При этом есть основания
предполагать, что ее порядок выше первого. Какой тест Вы будете использовать?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 22
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Коэффициент множественной детерминации и коэффициент множественной детерминации,
скорректированный на число степеней свободы. Связь между коэффициентом множественной детерминации и Fотношением.
2.
Модель с постоянными темпами роста (полу-логарифмическая модель).
3.
Тест множителей Лагранжа (LaGrange multiplyer test, LM-test, Breusch-Godfrey test) для обнаружения
автокорреляции произвольного порядка.
4.
Двухшаговый метод наименьших квадратов в сравнении с методом инструментальных переменных.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
0
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
10
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
-10 0
0.5
1
1.5
2
60
80
-20
X2 График остатков
20
10
0
-10
0
20
40
-20
X3 График остатков
20
10
0
-10 0
20
40
60
80
-20
В ходе оценки модели:
Yi    1 X i1   2 X i 2   3 X i 3   i
была выявлена существенная мультиколлинеарность. Исследователь решил ничего не предпринимать и оставить
модель как есть. Оправдано ли такое решение? Если да, то в каком случае? Если нет, то почему?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 33
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Доверительные интервалы оценок параметров и проверка гипотез о их значимости (t-тест) в рамках
классической линейной регрессии. Проверка адекватности регрессии (F-тест) в рамках классической линейной
регрессии.
2.
Методы борьбы с мультиколлинеарностью.
3.
Нарушение гипотезы о гомоскедастичности. Экономические причины гетероскедастичности. Последствия
гетероскедастичности для оценок коэффициентов регрессии методом наименьших квадратов и проверки
статистических гипотез.
4.
Стационарные и нестационарные временные ряды. Модель случайного блуждания. Кажущиеся тренды и
регрессии в случае нестационарных переменных.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
15
10
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
3.62
0
-5
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.187313 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
5
3.33049
0.63761
-0.9219
9.98292
0.0031753
0.5306194
0.3670751
2.00E-09
0
0.5
1
1.5
2
60
80
60
80
-10
-15
X2 График остатков
15
10
5
0
-5
0
20
40
-10
-15
X3 График остатков
15
10
5
0
-5
0
20
40
-10
-15
Объясните, каким образом Вы выберете лучшую спецификацию, оценив следующие четыре варианта:
(1) y  1  1 x  1 ;
y   2   2 ln x   2 ;
(3) ln y   3   3 x   3 ;
(4) ln y   4   4 ln x   4 .
(2)
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 34
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Влияние изменения масштаба измерения переменных на оценки коэффициентов регрессии и их дисперсий.
Регрессия в центрированных и нормированных переменных.
2.
Выбор между линейной и линейной в логарифмах моделью. Тест Бокса-Кокса (Box-Cox test). Преобразование
Зарембки (Zarembka scaling).
3.
Проверка гипотезы об отсутствии автокорреляции в авторегрессионных моделях с помощью h-статистики
Дарбина.
4.
Результаты Нельсона-Плоссера по анализу стационарности исторических рядов макроэкономической
динамики. Понятие о тесте Дикки-Фуллера.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
VIF
X1
X2
X3
2.04
1.23
2.92
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
6.
7.18135
3.35266
0.07313
0.08937
10
0
анализ
SS
MS
F
Значимость F
3 5253.8 1751.27 36.18731 1.76029E-08
21 1016.28 48.3945
24 6270.08
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
X1 График остатков
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
-10 0
0.5
1
1.5
2
60
80
-20
20
X2 График остатков
10
0
-10 0
20
40
-20
20
X3 График остатков
10
0
-10 0
20
40
60
80
-20
В ходе оценки модели:
Yi    1 X i1   2 X i 2   3 X i 3   i
была выявлена существенная мультиколлинеарность. Исследователь решил ничего не предпринимать и оставить
модель как есть. Оправдано ли такое решение? Если да, то в каком случае? Если нет, то почему?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 40
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Разложение суммы квадратов отклонений наблюдаемых значений зависимой переменной от ее
выборочного среднего. Дисперсионный анализ. Коэффициент детерминации и его свойства.
2.
Тесты Чау (Chow) на предсказательную силу модели и устойчивость коэффициентов.
3.
Нарушение гипотезы о гомоскедастичности. Бройша-Пейгана (Breusch-Pagan), Уайта (White).
4.
Модель коррекции ошибками для нестационарных коинтегрированных переменных.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
0
VIF
X1
X2
X3
2.04
9.23
11.22
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
10
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
По 1000 наблюдениям я оценил уравнение следующего вида:
-10 0
0.5
1
1.5
2
60
80
60
80
-20
X2 График остатков
20
10
0
-10 0
20
40
-20
X3 График остатков
20
10
0
-10 0
20
40
-20
yt  2.7 0.4 xt  0.9 yt 1 R 2  0.98 ,
(1.1)
( 0.1)
( 0.02)
DW  1.8 . Однако, несмотря на большое значение коэффициента детерминации и близкое к 2 значение
статистики Дарбина-Уотсона, мой друг мне сказал, что моя модель никуда не годится. Почему?
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 25
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Теорема Гаусса-Маркова для множественной линейной регрессии (без доказательства эффективности
оценок).
2.
Понятие о методе главных компонент, как средстве борьбы с мультиколлинеарностью данных.
3.
Понятие об автокорреляции случайной составляющей. Статистика Дарбина-Уотсона (Durbin-Watson),
условия ее применимости. Авторегрессионная схема 1-го порядка (марковская схема).
4.
Оценивание одновременных уравнений. Идентифицируемость уравнений. Критерии порядка и ранга.
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
X1 График остатков
20
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
1.92
0
VIF
X1
X2
X3
2.04
1.23
2.92
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
10
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
Была выполнена оценка регрессии для следующей модели:
-10 0
0.5
1
1.5
2
60
80
-20
X2 График остатков
20
10
0
-10
0
20
40
-20
X3 График остатков
20
10
0
-10 0
20
40
60
80
-20
y   0  1 x1   2 x2   3 x3   .
Объясните, каким образом следует проверять гипотезу об одновременном выполнении двух соотношений:
H 0 : 1   2 ;  3  1.
Заведующий кафедрой
Канторович Г.Г.
Кафедра математической экономики и эконометрики.
Экзамен по эконометрике.
Билет № 35
Ф.И.О.
Группа
(Впишите свою фамилию, имя и отчество, группу)
1.
Классическая линейная регрессия для случая одной объясняющей переменной. Статистические
характеристики (математическое ожидание, дисперсия и ковариация) оценок параметров.
2.
Сравнение двух регрессий с помощью фиктивных переменных и теста Чау (Chow). Эквивалентность этих
подходов.
3.
Нарушение гипотезы о гомоскедастичности. Тесты Парка (Park), Глейзера (Glejser)
4.
Оценивание моделей с распределенными лагами методом поиска на сетке (метод Клейна). Модель
гиперинфляции Кейгана (Cagan).
5.
Объясните, какие проблемы имеются у модели регрессии и как их исправить.
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный
0.91538
R
R-квадрат0.83792
Нормированный
0.81476
R-квадрат
Стандартная
6.95661
ошибка
Наблюдения
25
Дисперсионный
df
Регрессия
Остаток
Итого
Dw=
2.05
VIF
X1
X2
X3
2.04
9.23
11.22
анализ
SS
MS
F Значимость F
3 5253.8 1751.27 36.18731 1.8E-08
21 1016.28 48.3945
24 6270.08
tКоэффицие Стандартн статистик
нты
ая ошибка
а
P-Значение
Y-пересечение
23.9174
X1
2.13769
X2
-0.0674
X3
0.89221
6.
7.18135
3.35266
0.07313
0.08937
3.33049
0.63761
-0.9219
9.98292
0.003175
0.530619
0.367075
2.00E-09
15
10
5
0
-5 0
-10
-15
X1 График остатков
0.5
1
1.5
2
X2 График остатков
15
10
5
0
-5 0
-10
-15
20
40
60
80
60
80
X3 График остатков
15
10
5
0
-5 0
-10
-15
20
40
Оценивалась модель:
Yi    1 X i1   2 X i 2   i
При проведении теста серий расчетное значение статистики составило Z=+2.34. Объясните, как оно было
получено? Закончите тест и сделайте выводы.
Заведующий кафедрой
Канторович Г.Г.