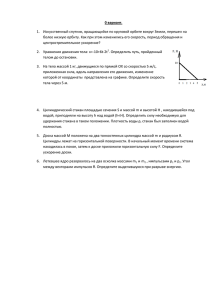
Точка движется вдоль оси с постоянным ускорением, проекция

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ ЯРОСЛАВА МУДРОГО»
Методическое пособие для организации самостоятельной работы
студентов по разделу «Механика»
Великий Новгород
2014
2
УДК 53 (0765)
Печатается по решению
РИС НовГУ
Рецензент
Методическое пособие для организации самостоятельной работы
студентов по разделу «Механика» /Сост. З.С. Бондарева, Р.П. Воронцова,
Г.Е. Коровина, Н.А. Петрова, Н.П. Самолюк: НовГУ им. Ярослава Мудрого.
– Новгород, 2014. – 124 с.
Сборник содержит задачи для самостоятельной работы студентов при подготовке
к аудиторным контрольным работам, к выполнению домашних контрольных работ, а
также при подготовке к защите лабораторных работ по механике поступательного и
вращательного движения. Материалы пособия могут быть использованы при
изучении не только общей физики, но и при изучении теоретической механики.
Кроме того, материалы пособия могут быть использованы для составления
контрольных работ разного уровня. Выбор той или иной формы использования
материала определяется преподавателем в зависимости от образовательного
стандарта. Так как в пособие включены задачи разного уровня сложности, материалы
пособия могут быть использованы преподавателями всех специальностей, в учебные
стандарты которых входит изучение физики.
Сборник предназначен для студентов всех специальностей дневной и заочной
формы обучения.
УДК 53 (0765)
©Новгородский государственный
университет, 2014
© З.С. Бондарева, Р.П. Воронцова, Г.Е.
Коровина,
Н.А.
Петрова,
Н.П.
Самолюк
составление, 2014
3
Содержание
Предисловие
1. Кинематика материальной точки
2. Кинематика вращательного движения
3 Криволинейное движение тела в поле силы тяжести
4. Динамика поступательного движения
5. Механический удар
6. Динамика вращательного движения тела вокруг
неподвижной оси
7. Момент инерции
8 Маятник Обербека
9. Определение момента инерции тел с помощью
крутильных колебаний
10. Баллистический и крутильно-баллистический маятники
Литература
Стр.
4
5
13
36
37
42
55
75
93
104
108
124
4
Предисловие
Последние государственные образовательные стандарты высшего
профессионального образования делают основной упор на индивидуальную
и самостоятельную работу студентов. В предлагаемом методическом
пособии содержатся задания для индивидуальной и самостоятельной работы
студентов. Эти задания могут быть использованы студентами при изучении
соответствующих тем раздела «Механика». Кроме того, эти задания могут
быть использованы для составления домашних и аудиторных контрольных
работ по различным темам курса, а также могут быть использованы при
защите лабораторных работ. Задания, предложенные в пособии, могут быть
включены в экзаменационные вопросы и билеты по изучаемому разделу.
Кроме того, материалы пособия могут быть использованы при выполнении и
защите заданий учебной практики по механике.
Задания составлены в соответствии с темами учебного курса. В
пособии использована различная форма представления заданий. Часть
заданий сформулирована в виде классических задач. Некоторые задания
представлены как многовариантные контрольные работы. В пособие
включены задания, оформленные в виде тестов. Такое разнообразие форм
представления заданий позволяет студентам осваивать различные виды
контроля знаний и различные формы представления результатов решения
задач.
В пособии использованы материалы известных задачников. В пособие
включены задания, подготовленные в НовГУ в пособии «Сборник заданий
для автоматизированной обучающей системы по общему курсу физики.
Механика. Часть I. – Новгород, 1995 год». Кроме того, в пособие включены
задания, которые использовались при защите лабораторных работ
студентами физической специальности.
Пособие может быть использовано преподавателями, ведущими курс
физики на различных специальностях, так как оно содержит задачи разного
уровня сложности. Кроме того, пособие может быть использовано учителями
физики для проведения уроков решения задач и для подготовки учащихся к
сдаче единого государственного экзамена. Предлагаемое пособие может быть
использовано студентами направления «Педагогическое образование.
Профиль Физика и информатика» во время прохождения педагогической
практики для подготовки к урокам физики и для проведения кружковых и
дополнительных занятий по решению задач.
5
1. Кинематика материальной точки
Задача 1
Материальная точка движется вдоль оси OX так, что проекция ее
скорости на ось OX изменяется со временем по закону:
a  Vx  10  2t;
b V
c V
 2t ;
d V
 0  2t ;
x  0 , 5t ;
x 1 0
x  1
e  Vx  10  2t (величины измерены в единицах «СИ»).
Для каждого случая выполнить следующие задания:
а) описать характер движения точки;
б) найти величину и направление начальной скорости точки;
в) найти проекцию ускорения на ось OX , указать величину ускорения
и его направление;
г) определить скорость точки через 5 с и через 10 с от начала движения,
указать величину и направление скорости в эти моменты времени;
д) построить график зависимости проекции скорости на ось OX от
времени;
е) построить график зависимости модуля скорости точки от времени;
ж) построить график зависимости проекции ускорения на ось OX от
времени;
з) построить график зависимости модуля ускорения от времени;
и) останавливалось ли тело? Если тело останавливалось, то определите,
в какой момент времени это происходило?
к) каков характер движения тела до остановки и после остановки?
л) определите по графикам проекцию скорости и модуля скорости
скорость в начальный момент времени и при t =2c и 5c;
м) какой точке графика проекции скорости на ось OX , и какой точке
графика модуля скорости точки соответствует остановка точки в
процессе движения?
н) запишите зависимость координаты движущейся точки от времени,
считая, что движение начиналось из начала координат; из точки с
координатой x  3м; x  1м
Задача 2
Уравнение координаты материальной точки, движущейся вдоль оси
OX , имеет вид:
1 x  10 ; 2  x  5t; 3 x  10  5t; 4  x  10  5t; 5 x  10  5t;
6  x  2t 2 ; 7  x  t 2 ; 8 x  5t  2t 2 ; 9  x  5t  2t 2 ; 10  x  5t  2t 2 ;
11 x  5t  2t 2 ; 12  x  10  5t  2t 2 ; 13 x  10  5t  2t 2 ;
14  x  10  5t  2t 2 ; 15 x  10  5t  2t 2 ; 16  x  10  5t  2t 2 ;
6
17  x  10  5t  2t 2 ;
18 x  10  5t  2t 2 ;
19  x  10  5t  2t 2 ;
20  x  10  2t 2 ; 21 x  10  2t 2 ; 22  x  10  2t 2 ; 23 x  10  2t 2 .
(Все величины измерены в единицах системы единиц «СИ»). Для этих
случаев движения выполнить следующие задания:
1) найти начальную координату движущихся точек;
2) определить зависимость проекции скорости точки как функцию времени;
3) определить величину и направление начальной скорости точки;
4) построить график проекции скорости точки как функции времени;
5) построить график модуля скорости точки как функции времени;
6) останавливалась ли точка при своем движении; определите момент
остановки;
7) опишите характер движения точки до остановки и после остановки;
8) определите проекцию ускорения точки на ось OX ;
9) определите величину и направление ускорения; как эти данные
характеризуют особенности движения точки;
10) построить графики проекции ускорения на ось OX и модуля ускорения;
11) определить координату точки в момент времени 2 с;
12) определить путь, пройденный точкой за 2 с;
13) определить перемещение точки за 2 с.;
14) определить графически и аналитически моменты времени, когда
скорость точки была равна 5 м/с;
15) построить графики координаты точки как функции времени;
16) построить график пути, пройденного телом от начала движения, в
зависимости от времени;
17) аналитически и графически определить моменты времени, когда
координата тела была равна –5 м (минус пять метров);
18) за какое время точка пройдет от начала движения путь 10 м?
19) что показывают точки пересечения графика проекции скорости и
модуля скорости с осями координат?
20) что показывают точки пересечения графика координаты с осями
координат?
Задача 3
Координаты двух движущихся тел описываются выражениями:
x1  10t  4t 2 , x2  6t  2t 2
Здесь координаты измеряются в метрах, а время в секундах. Описать
движение каждого тела.
1. Найти время и место встречи тел;
2. Найти момент времени, когда скорости тел будут равны по величине;
3. Найти момент времени, когда скорости тел равны по величине и
совпадают по направлению;
7
4. Где будет второе тело в тот момент, когда координата первого тела будет
равна - 24 м? (минус двадцать четыре метра).
5. В какой момент времени первое тело будет в той точке, в которой второе
тело будет через 0,5 с после начала движения?
6. Где будет первое тело в тот момент времени, когда скорость второго тела
будет равна 10 м/с?
7. Где будет каждое тело через 3 секунды после начала движения? Каково
расстояние между телами в этот момент времени?
8. В какой момент времени расстояние между телами будет равно 32 м?
9. По какому закону изменяется со временем расстояние между телами?
10.Построить графики координат тел, проекций скоростей тел на ось OX ,
модулей скоростей тел, проекций ускорений и модулей ускорений как
функций времени.
11.Что показывают точки пересечения названных графиков с осями
координат?
12.Решите перечисленные задачи с помощью графиков
13.Какое из тел раньше окажется в точке с координатой x  4 м и на какое
время раньше?
14.Чему равны и как направлены скорости тел в точке с координатой x  4 м ?
На сколько отличаются модули скоростей тел в этой точке?
15.Будут ли тела останавливаться при таких движениях? Когда произойдет
остановка первого и второго тела? Какое тело остановится раньше и
насколько раньше?
Задача 4
Во сколько раз путь, пройденный телом за три секунды при равноускоренном
движении без начальной скорости, больше пути пройденного этим телом за
третью секунду своего движения?
Задача 5
Во сколько раз время, за которое равноускорено движущееся тело проходит
10 м, больше времени, за которое это тело проходит десятый метр своего
пути? Начальная скорость тела равна нулю.
Задача 6
За какое время равноускорено движущееся без начальной скорости тело
пройдет n  ый метр своего пути? Какой путь проходит это тело за n  ую
секунду своего движения?
Задача 7
Тело, двигаясь равноускорено из состояния покоя, проходит за четвертую
секунду от начала движения 7 м. Какой путь пройдет тело за первые 10
секунд? Какой скорости оно достигнет к концу десятой секунды?
8
Задача 8
Во сколько раз скорость пули в середине ствола ружья меньше, чем при
вылете из ствола?
Задача 9
Материальная точка, движущаяся равноускорено из состояния покоя, прошла
за время t1 путь S1. За какое время от начала движения она пройдет путь S2?
Задача 10
Расстояние между двумя станциями поезд прошел со средней скоростью 72
км/ч за 20 мин. Разгон и торможение вместе длились 4 мин, а остальное
время поезд двигался равномерно. Какой была скорость поезда при
равномерном движении? Задачу решить аналитически и графически.
Задача 11
Тело свободно падает с высоты 80 м. Каково его перемещение в последнюю
секунду падения?
Задача 12
Сколько времени падало тело, если за последние 2с оно прошло 60 м? С
какой высоты падало тело?
Задача 13
Одно тело свободно падает с высоты h1 ; одновременно с ним другое тело
начинает движение с большей высоты h2  h1 . Какова должна быть начальная
скорость второго тела, чтобы оба тела упали одновременно?
Задача 14
Из точки, расположенной на достаточно большой высоте, одновременно
брошено два тела с одинаковыми по модулю скоростями V0  2 м : одно
с
вертикально вверх, а другое вертикально вниз. Определите расстояние между
телами как функцию времени. Каким будет это расстояние между телами
через 1 с и через 5 с?
Задача 15
Тело брошено вертикально вверх со скоростью 30 м/с. На какой высоте и
через какое время после начала движения скорость тела по модулю будет в
три раза меньше, чем в начале подъема?
9
Задача 16
Тело брошено вертикально вверх со скоростью 20 м/с. Написать уравнение
y  y  t  . Найти, через какой промежуток времени тело будет на высоте а) 15
м; б) 20 м; в) 25 м. Ось OY направлена вертикально вверх и при t  0 y  0 .
Задача 17
С балкона, находящегося на высоте 25 м над поверхностью земли, бросили
вертикально вверх мячик со скоростью 20 м/с. Написать формулу
зависимости координаты y от времени, выбрав за начало отсчета: а) точку
бросания; б) поверхность земли. Найти, через какой промежуток времени
мячик упадет на землю.
Задача 18
Тело падает с некоторой высоты и проходит последние 196 м пути за 4 с. С
какой высоты и сколько времени падало тело?
Задача 19
Свободно падающее тело в последнюю секунду своего падения проходит
половину пути. Определить время и высоту падения.
Задача 20
За последнюю секунду свободно падающее тело прошло 3 4 своего пути.
Сколько времени падало тело?
Задача 21
Два тела начинают одновременно падать из двух разных точек,
расположенных на одной вертикали. Показать, что при свободном падении
расстояние между ними остается неизменным.
Задача 22
С некоторой высоты свободно падает тело. Через две секунды с той же
высоты падает второе тело. Через какое время от начала движения второго
тела расстояние, разделяющее тела до начала падения второго тела,
удвоится?
Задача 23
Построить график зависимости проекции скорости на вертикальную ось тела,
брошенного вертикально вверх со скорость 40 м/с, если: а) ось OY
направлена вертикально вверх; б) ось OY направлена вниз.
Задача 24
Тело, начавшее двигаться равноускорено из состояния покоя, проходит за
первую секунду своего движения путь S. Какой путь оно пройдет за вторую,
третью, четвертую и пятую секунды?
10
Задача 25
Найти модуль вектора перемещения материальной точки, скорость которой
изменяется по закону V  2  2t (м/с), через 4 секунды после начала
движения. Определить путь, пройденный точкой за это время.
Задача 26
Скорость прямолинейного движения материальной точки подчиняется
закону V  2t . Определить, за какое время точка сместится на расстояние 9 м
от точки начала движения.
Задача 27
Величина скорости тела за одну секунду увеличилась в два раза. Во сколько
раз увеличится скорость тела за следующую секунду, если ускорение тела
постоянно?
Задача 28
Точка движется вдоль оси OX так, что ее координата изменяется со
временем по закону x  5  4t  2t 2 (м). Найти координату точки, в которой
скорость станет равной нулю.
Задача 29
Точка движется вдоль оси OX с постоянным ускорением, проекция которого
на ось равна a x   1 м / с 2  . Проекция скорости точки на ось OX в
начальный момент времени
пройденный точкой за 5 с.
равна
Vx  2  м / с  .
Определить
путь,
Задача 30
Точка движется вдоль оси OX с ускорением, проекция которого на ось OX
равна a x  1  м / с 2  . Проекция начальной скорости точки на ось OX равна
Vx  3  м / с  . Определить путь, который пройдет точка за 4 секунды от
начала движения.
Задача 31
Пуля, летящая со скоростью 141 м/с, попадает в доску и проникает на
глубину 6 см. Пуля в доске двигалась с постоянным ускорением. Определить
скорость пули на глубине 3 см.
Задача 32
Мяч брошен вертикально вверх из точки, находящейся на высоте h . За время
движения мяч пролетел путь 3h . Определить модуль начальной скорости
мяча.
11
Задача 33
При равнозамедленном торможении автомобиль проходит за пятую секунду
путь 5 см и останавливается. Какой путь прошел этот автомобиль за третью
секунду своего торможения?
Задача 34
Какие из приведенных зависимостей от времени пути и модуля скорости
описывают равноускоренное прямолинейное движение:
1) V  4  2t; 2) S  3  5t; 3) S  5t 2 ; 4) 4) S  3t  2t 2 ; 5) 5) V  2  3t  4t 2 ?
Задача 35
Мяч брошен вертикально вверх со скоростью 20 м/с. Через сколько секунд
нужно бросить вверх второй мяч со скоростью в два раза меньшей, чтобы
они встретились в наикратчайшее время?
Задача 36
По заданной графической зависимости проекции скорости на некоторую ось
от времени (Рис. 1) найти аналитическую зависимость проекции ускорения
от времени, модуля ускорения от времени, аналитическую зависимость
проекции скорости от времени и модуля скорости от времени. Определить
аналитическую зависимость координаты от времени. Движение точки
прямолинейное и начинается в начале оси координат.
4
10
20
-4
Рис.1
30
t, c
12
Примечание: данную задачу можно формулировать по вариантам или в виде
индивидуальных заданий, выделяя для разных вариантов или разных заданий
отдельные участки графика.
Задача 37
По заданной графической зависимости проекции скорости на некоторую ось
от времени (Рис. 2) найти аналитическую зависимость проекции ускорения
от времени, модуля ускорения от времени, аналитическую зависимость
проекции скорости от времени и модуля скорости от времени. Определить
аналитическую зависимость координаты от времени. Движение точки
прямолинейное и начинается в начале оси координат.
Vx, м/c
20
0
10
20
30
t, c
-20
Рис.2
Примечание: данную задачу можно формулировать по вариантам или в виде
индивидуальных заданий, выделяя для разных вариантов или разных заданий
отдельные участки графика.
Задача 38
Два тела двигаются со скоростями V1  V2  10 м/с, составляющими угол  .
Определить относительную скорость шаров для следующих случаев:
1)  = 600; 2)  =1800; 3)  =00; 4)  =900; 5)  =1200; 6)  =300; 7)  =450.
13
Задача 39
Два тела имеют одинаковые по величине скорости V1  V2  10 м/с.
Относительная скорость тел равна по модулю Vотн = 10 м/с. Чему равен угол
между векторами скорости V1 и V2 ?
2 Кинематика вращательного движения
Задача 40
Материальная точка движется по окружности радиуса R  2 м , причем ее
линейная скорость зависит от времени так, как показано на рисунках 1 и 2.
Для каждого участка этих графиков построить графики зависимости:
 Угла поворота от времени,     t  ;
 Угловой скорости от времени,     t  ;
 Углового ускорения от времени,     t  ;
 Нормального ускорения от времени, an  an  t  ;
 Тангенциального ускорения от времени, a  a t  ;
 Пути от времени, S  S  t  .
Для каждого участка вычислить полное ускорение, перемещение и угол
между скоростью и полным ускорением через 2 с после начала движения на
соответствующем участке графика скорости.
Задача 41
Через какой промежуток времени совпадают часовая и минутная стрелка
часов?
Задача 42
Во сколько раз нормальное ускорение точки, лежащей на ободе
вращающегося колеса, меньше ее тангенциального ускорения для момента
времени, когда вектор полного ускорения точки составляет угол 300 с
вектором ее линейной скорости?
Задача 43
Материальная точка движется по окружности радиуса R  2 м . Зависимость
угла между радиус–вектором и некоторым выбранным направлением
определяется функцией   t   At 2  Bt  C , где A  2 рад / c2 , B  3 рад / c ,
C  1рад . Определить угловую и линейную скорость, нормальное,
тангенциальное, полное ускорение и угловое ускорение, путь, угол между
линейной скоростью и полным ускорением через 2 с после начала движения.
14
Задача 44
Для определения скорости пули используются два диска на одной оси,
вращающиеся с одной скоростью. Какова скорость пули, если она, пролетая
через отверстие в первом диске, оставляет след на втором диске, смещенный
относительно отверстия на первом диске на угол   200 . Расстояние между
дисками равно 1 м. Частота вращения дисков 100 об/мин.
Задача 45
Что необходимо знать для определения направления и величины вектора
углового ускорения тела при его вращении вокруг неподвижной оси? Указать
правильные ответы.
1. Ориентацию оси вращения;
2. Направление вектора силы;
3. Направление и величину момента внешней силы;
4. Момент инерции тела;
5. Массу тела.
Задача 46
Что необходимо знать для определения направления и величины вектора
углового ускорения тела при его вращении вокруг неподвижной оси? Указать
правильные ответы.
6. Ориентацию оси вращения;
7. Направление вектора силы;
8. Направление и величину момента внешней силы;
9. Момент инерции тела;
10.Массу тела.
Задача 47
Используя график зависимости угловой скорости вращения тела от времени
(Рис. 3), определите величину углового ускорения для каждого интервала
времени.
15
8
6
4
2
0
1
2
3
4
5
6
t, c
Рис.3
Задача 48
На рисунке (Рис. 4) представлена зависимость угловой скорости
вращающегося тела от времени. Определите, во сколько раз угловое
ускорение в интервале времени от t  1 с до t  2 с меньше, чем в интервале
времени от t  3 с до t  4 с.
8
6
4
2
0
1
2
4
3
Рис. 4
5
6
t,c
16
Задача 49
На рисунке 5 представлены графики зависимости угловой скорости для
вращающихся тел. На всех графиках единицы измерения угловой скорости и
времени одни и те же. Определить:
1. У какого тела угловое ускорение максимально;
2. У какого тела угловое ускорение минимально;
3. У каких тел угловое ускорение одинаково.
17
1
4
3
2
1
0
1
2
3
4
5
t
0
2
4
6
8
10
t
2
8
6
4
2
18
3
8
6
4
2
0
1
2
3
4
5
t
0
1
2
3
4
5
t
4
4
3
2
1
19
5
8
6
4
2
0
1
2
3
4
5
t
Рис. 5
Задача 50
Укажите, какой график зависимости углового ускорения от времени для
вращающегося тела соответствует приведенному на рисунке 6 графику
зависимости угловой скорости от времени. На графиках величины угловой
скорости  , углового ускорения  и времени t представлены в единицах
системы СИ.
20
6
4
2
0
1
2
3
4
t
21
1
6
4
2
0
1
2
3
4
t
0
1
2
3
4
t
2
6
4
2
22
3
6
4
2
0
1
2
3
4
t
0
1
2
3
4
t
4
6
4
2
23
5
6
4
2
0
1
2
3
4
t
Рис. 6
Задача 51
Какой график зависимости угловой скорости от времени соответствует
графику зависимости углового ускорения от времени (Рис. 7). На графиках
величины угловой скорости  , углового ускорения  и времени t
представлены в единицах системы СИ.
3
2
1
0
-1
-2
1
2
3
4
t
24
1
6
4
2
0
1
2
3
4
t
2
6
4
2
0
1
2
3
4
t
25
3
6
4
2
0
1
2
3
4
t
0
1
2
3
4
t
4
6
4
2
5
6
4
2
0
1
2
Рис. 7
3
4
t
26
Задача 52
Укажите, какой график зависимости углового ускорения от времени для
вращающегося тела соответствует приведенному на рисунке 8 графику
зависимости угловой скорости от времени. На графиках величины угловой
скорости  , углового ускорения  и времени t представлены в единицах
системы СИ.
27
6
4
2
0
1
2
3
4
t
3
4
t
1
6
4
2
0
2
1
-2
2
6
4
2
0
-2
1
2
3
4
t
28
3
4
2
0
1
2
3
4
t
1
2
3
4
t
-2
4
6
4
2
0
-2
-4
5
4
2
0
1
2
-2
Рис. 8
3
4
t
29
Задача 53
Какой график зависимости угловой скорости от времени соответствует
графику зависимости углового ускорения от времени (Рис. 9). На графиках
величины угловой скорости  , углового ускорения  и времени t
представлены в единицах системы СИ.
6
4
2
0
1
3
2
4
t
-2
1
4
2
0
2
1
3
4
t
2
4
2
0
1
2
3
4
t
30
3
6
4
2
0
1
2
3
t
4
4
6
4
2
0
1
2
3
4
t
5
6
4
2
0
1
2
3
Рис. 9
4
t
31
Задача 54
Какой график (Рис. 10) зависимости угловой скорости от времени
соответствует графику зависимости углового ускорения от времени. На
графиках величины угловой скорости  , углового ускорения  и времени t
представлены в единицах системы СИ.
32
4
2
0
1
2
3
4
-2
1
6
4
2
0
1
2
3
4
1
2
3
4
2
6
4
2
0
33
3
6
4
2
0
1
2
4
3
4
6
4
2
0
1
2
3
4
1
2
3
4
5
6
4
2
0
Рис. 10
34
Задача 55
Какой график зависимости угловой скорости от времени соответствует
графику зависимости углового ускорения от времени (Рис.11). На графиках
величины угловой скорости  , углового ускорения  и времени t
представлены в единицах системы СИ.
6
4
2
0
1
2
3
4
1
4
2
0
1
2
3
4
1
2
3
4
-2
2
4
2
0
35
3
8
4
0
1
2
3
4
3
4
-4
4
4
2
0
1
2
-2
5
6
4
2
0
1
3
2
-2
Рис. 11
4
36
3 Криволинейное движение тела в поле силы тяжести
Задача 56
Миномет стреляет с высоты h . Начальная скорость снаряда равна V0 и
направлена под углом  к горизонту. Найти значения нормального и
тангенциального ускорения и вычислить радиус кривизны траектории в
момент времени t1 после выстрела. Сопротивлением воздуха пренебречь.
Ускорение свободного падения принять равным 10 м/с2. Числовые данные
указанных параметров взять из таблицы 1.
Таблица 1
№
п/п
1
2
3
4
5
6
7
8
9
10
h, м
V0 , м / с
 ,0
t1 , c
t2 , c
0
50
100
0
50
100
0
50
100
0
100
125
150
175
200
250
125
100
100
200
30
45
60
30
45
60
45
30
60
45
2
4
6
4,5
8
7
2
1
2
2
2,5
4,2
5,0
5,5
4,4
5
2,5
1,5
2,5
2,5
Для каждого случая вычислить полное время движения мины, наибольшую
высоту подъема, дальность полета по горизонтали, а также перемещение
мины. Определить, под каким углом к горизонту мина упадет на землю. Для
каждого случая вывести уравнение траектории движения мины.
Задача 57
Минометная батарея расположена у подножья горы с углом наклона 45 0 к
горизонту. Под каким углом к горизонту надо установить ствол орудия,
чтобы мина достигла склона на максимальной высоте. Сопротивление
воздуха не учитывать.
37
4. Динамика поступательного движения
Задача 58
На рельсах стоит платформа с орудием. Масса платформы вместе с орудием
1000 кг. Из орудия произведен выстрел снарядом 10 кг. Скорость снаряда
при вылете из орудия направлена горизонтально и равна 100 м/с. Определить
расстояние, на которое откатилась платформа и время ее движения до
остановки после выстрела, если коэффициент трения между колесами
платформы и рельсами равен   0,02 .
Задача 59
H
на
2
тело действует постоянная сила F  5 H , совпадающая по направлению с
силой тяжести. Найти: а) уравнение движения тела; б) время падения на
землю; в) максимальную скорость падения; г) построить график зависимости
координаты от времени; д) на сколько градусов изменится температура
одного литра воды при падении тела в воду.
Тело массой 1 кг свободно падает с высоты H  100 м. На высоте h 
Задача 60
Импульс тела массой M в три раза больше импульса тела массой m , а
кинетическая энергия второго тела в два раза больше, чем кинетическая
M
энергия первого тела. Найти отношение масс
этих тел.
m
Задача 61
H
на
2
тело действует постоянная сила F  5 H , противоположная направлению
силы тяжести. Найти: а) уравнение движения тела; б) время падения на
землю; в) максимальную скорость падения; г) построить график зависимости
координаты от времени; д) на сколько градусов изменится температура
одного литра воды при падении тела в воду.
Тело массой 1 кг свободно падает с высоты H  100 м. На высоте h 
Задача 62
С наклонной плоскости высотой 10 м без трения скатывается из состояния
покоя платформа с пушкой общей массой 100 кг. В середине пути из пушки
произведен выстрел снарядом массой 10 кг. Снаряд вылетел горизонтально
со скоростью 100 м/с. Какова скорость платформы в конце наклонного пути?
Какое количество теплоты выделится при неупругом столкновении этой
платформы с аналогичной неподвижной платформой, находящейся у
основания наклонной плоскости? Угол наклона плоскости к горизонту равен
300.
38
Задача 63
С высоты 5 м скользит тело по наклонному желобу, переходящему в
окружность (Рис. 12). Определить скорость тела в момент отрыва от желоба.
Найти максимальную высоту подъема тела и кинетическую энергию в
наивысшей точке траектории. Трением пренебречь. Масса тела равна 0,5 кг.
m
H
H
Рис. 12
Задача 64
Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком
стержне, и застревает в нем. Масса пули в 20 раз меньше массы шара. Длина
стержня 1 м. Определить скорость пули, если стержень отклонился на угол
  100 .
Задача 65
На горизонтальном столе лежит тело массой m1  100 г. Тело связано нитью,
переброшенной через блок, с другим грузом массой m2  150 г. Считая что в
системе отсутствуют силы трения и массой блока можно пренебречь, найти
ускорение тел и силу натяжения нити. (Рис. 13).
Рис. 13
39
Задача 66
Скорость ветра равна V0  10 м/с. Ветер действует на парус с силой, величина
S  V0  V 
которой определяется формулой F 
. Здесь S - площадь паруса,
2
  1,2 кг/м3 – плотность воздуха, V - скорость судна. Определить скорость
судна, при которой мощность ветра максимальна. Найти максимальную
мощность ветра, а также работу силы ветра за 10 с.
2
Задача 67
Маленький шарик, подвешенный на нити длиной l  1 м, отклонили на угол
  600 от вертикали и отпустили без начальной скорости. Определите
скорость шарика в момент прохождения положения равновесия.
Задача 68
Деревянный стержень массой 1 кг лежит на штативе, верхняя часть которого
выполнена в виде кольца. Снизу в шар попадает пуля, летящая вертикально.
Пуля пробивает шар, и он поднимается на высоту H  1 м над кольцом. На
какую высоту над кольцом поднимется пуля, если ее скорость перед ударом
была 100 м/с. Масса пули равна 10 г. изменением массы шара пренебречь.
Задача 69
Теннисный мяч, падает без начальной скорости с высоты h  2 м. после
каждого отскока от пола он поднимается на высоту hn  0,8hn 1 . На какую
высоту он поднимется после третьего отскока?
Задача 70
Санки, движущиеся по льду со скоростью 10 м/с, вылетают на асфальт.
Длина полозьев санок равно 0,9 м, коэффициент трения санок об асфальт
равен   0,8 . Какой путь пройдет передний конец полозьев санок по
асфальту до полной остановки? Масса санок распределена по длине санок
равномерно.
Задача 71
С наклонной плоскости высотой H  3 м соскальзывает шайба. В конце
спуска шайба ударяется о стенку (Рис. 14). Считая удар абсолютно упругим,
определить на какую высоту поднимется шайба. Угол наклона плоскости к
горизонту равен   300 . Коэффициент трения шайбы о плоскость равен
  0,05
40
H
Рис. 14
Задача 72
Для определения коэффициента трения можно воспользоваться установкой,
представляющей собой горизонтальную вогнутую сферическую поверхность
с нанесенными градусными метками. Тело устанавливают на поверхности
так, чтобы радиус, проведенный их центра сферической поверхности в центр
масс тела, составлял с вертикалью угол   300 . Тело отпускают без
начальной скорости, и оно скользит под действием собственного веса по
сферической поверхности, поднимаясь на угол   200 . Найти коэффициент
трения тела по сферической поверхности.
Задача 73
Брусок массой m  2 кг тянут по горизонтальной поверхности, прикладывая
силу F  5H . При этом брусок за время t  30c изменил свою скорость от
V1  2 м/c до V2  4 м/c, двигаясь ускоренно в одну сторону. Найти
коэффициент трения бруска о поверхность.
Задача 74
Ледяная гора составляет с горизонтом угол   300 . По ней пускают снизу
вверх камень, который в течение t  2c проходит расстояние L  15 м, после
чего соскальзывает вниз. Какой промежуток времени t длится
соскальзывание камня вниз? Каков коэффициент трения между горой и
камнем?
Задача 75
Человек массой m1  60 кг прыгает с неподвижной тележки, стоящей на
рельсах, вдоль рельс. При этом тележка массой m2  20 кг, откатывается в
противоположном направлении на расстояние L  2 м. Коэффициент трения
колес тележки о рельсы равен   0,1 . Какую работу совершил человек при
прыжке?
Задача 76
При падении тела массой m  1 кг с большой высоты его скорость при
установившемся движении равна V1  100 м/c. Определить время t , за
41
которое, начиная от момента падения, скорость тела становится равной
V2  0,5V1 . Силу сопротивления воздуха принять пропорциональной скорости
тела. Определить коэффициент сопротивления  .
Задача 77
Груз массой m  2 кг, висящий на нити, отклоняют на угол   600 . Найти
силу натяжения нити в момент прохождения телом положения равновесия.
Задача 78
Вода течет по горизонтальной трубе с закруглением радиусом R  10 м на
конце трубы таким, что конец трубы направлен вниз. Найти силу давления
воды на стенку трубы в закруглении. Диаметр трубы d  10 см. Через
поперечное сечение трубы за один час протекает m  300 тонн воды.
Плотность воды   103 кг м3 .
Задача 79
Гирька массой m  100 г, привязанная к резиновому шнуру длиной l0 ,
описывает в горизонтальной плоскости окружность (Рис.
). Частота
вращения гирьки   2 об . Угол отклонения резинового шнура от вертикали
с
0
  40 . Найти длину l0 нерастянутого шнура. Для растяжения шнура на 1 см
требуется сила 6 Н (Рис. 15).
Рис. 15
42
5 Механический удар
Задача 80
Горизонтально летящая пуля массой 10 г попадает в деревянный куб.
находящийся на горизонтальной поверхности. Определить, какая часть
энергии пули перешла в теплоту. Вычислить количество теплоты,
выделившееся при таком столкновении. Начальная скорость пули V0  200
м/с. Скорость пули после вылета из куба равна V1  0,5V0 . Масса куба равна 1
кг. Траектория пули проходит через центр тяжести куба. Трение между
кубом и горизонтальной поверхностью отсутствует. Изменением массы куба
в процессе столкновения пренебречь.
Задача 81
Шар массой m =0,5 кг, летящий со скоростью V = 2 м/с под углом 300 к
вертикальной стене, упруго сталкивается с ней и отлетает обратно под тем же
углом. Найти изменение импульса шара и импульс силы, действующей на
шарик со стороны стенки.
Задача 82
Шары A и B подвешены на нитях одинаковой длины так, что в состоянии
устойчивого равновесия они соприкасаются, и линия, соединяющая центры
шаров, проходит через точку соприкосновения шаров. Шар A отвели на
некоторый угол таким образом, что центр его тяжести поднялся на высоту
h1 = 8 см, и отпустили без начальной скорости. после неупругого соударения
с шаром B шары поднялись на высоту h2 =2 см. Найти отношение массы
шара A к массе шара B .
Задача 83
Два тела массами 2 кг и 1 кг движутся навстречу друг другу со скоростями
V1  2 м/с и V2  1 м/с. Определить количество теплоты, выделившееся при
абсолютно неупругом ударе тел.
Задача 84
Два тела массами 2 кг и 1 кг движутся друг за другом со скоростями V1  2
м/с и V2  1 м/с. Определить количество теплоты, выделившееся при
абсолютно неупругом ударе тел.
Задача 85
Два тела массами 2 кг и 1 кг движутся навстречу друг другу со скоростями
V1  2 м/с и V2  1 м/с. Определить скорости тел после абсолютно упругого
удара тел.
43
Задача 86
Два тела массами 2 кг и 1 кг движутся друг за другом со скоростями V1  2
м/с и V2  1 м/с. Определить скорости тел после абсолютно упругого удара.
Задача 87
Шары A и B подвешены на нитях одинаковой длины так, что в состоянии
устойчивого равновесия они соприкасаются, и линия, соединяющая центры
шаров, проходит через точку соприкосновения шаров. Шар A отвели на
некоторый угол таким образом, что центр его тяжести поднялся на высоту
h1 = 9 см, и отпустили без начальной скорости. После упругого соударения с
шаром B шар A поднялся на высоту h2 =1 см, а шар B - на высоту h1 =16 см.
Найти отношение массы шара A к массе шара B . Потерями энергии
пренебречь.
Задача 88
Два шара массами m1 и m2 движутся по одной прямой навстречу друг другу
со скоростями V1 =1,2 м/с и V2 =0,6 м/с. Шары сталкиваются упруго. Скорости
шаров после столкновения равны U1 =0,6 м/c и U 2 =0,8 м/с. После соударения
скорости направлены также как и скорость первого шара. Определить
отношение масс шаров.
Задача 89
Движущийся шар массой m абсолютно упруго ударяется о покоящийся шар
массой 3m . После удара шар массой m движется в противоположную
сторону. Во сколько раз изменилась скорость шара массой m ?
Задача 90
Какие из приведенных ниже утверждений относятся к абсолютно неупругому
взаимодействию?
1. Выполняются законы сохранения импульса и механической энергии
2. Выполняется только закон сохранения энергии
3. Выполняется только закон сохранения импульса
4. Не выполняется закон сохранения механической энергии и
выполняется закон сохранения импульса
Задача 91
Укажите, какие из приведенных утверждений описывают замкнутую
систему:
1. На сталкивающиеся тела не действуют внешние силы;
2. Система тел замкнутая, если действие на нее всех внешних сил
взаимно скомпенсированы;
44
3. В замкнутой системе тел проекция внешних сил на выбранное
направление движения тел равна нулю;
4. В момент соударения шаров развивается сила, во много раз
превышающая действие внешних сил.
Задача 92
Два стальных шара сталкиваются упруго. За время удара сила
взаимодействия изменяется по закону, представленному на графике (Рис. 16).
F, H
400
300
200
100
2
4
6
8
t, мс
Рис. 16
Определите:
1. Полный импульс, который получил каждый шар за время удара;
2. Среднюю силу взаимодействия шаров.
Задача 93
Два одинаковых стальных шара массой m  0,2 кг сталкиваются абсолютно
упруго. Сила взаимодействия шаров от времени представлена на рисунке 17.
F, H
400
300
200
100
2
4
6
8
Рис. 17
Определите:
t, мс
45
1. Изменение импульса каждого шара за время взаимодействия;
2. Скорость первого шара до удара, если второй шар до удара находился в
покое;
3. Среднюю силу взаимодействия шаров.
Задача 94
Сила, действующая на теннисный мяч при ударе ракеткой, зависит от
времени так, как показано на рисунке (Рис. 18)
F, H
300
200
100
20
40
60
t, мс
Рис. 18
Используя график, определите:
1. Импульс, полученный мячом за время контакта с ракеткой;
2. Среднюю силу, действующую на мяч во время удара;
3. Скорость мяча после удара, если его масса m  0,06 кг, а скорость его
до удара равна нулю.
Задача 94
Предположим, что сила, действующая на теннисный мяч массой m  0,06 кг,
зависит от времени так, как показано на рисунке (Рис. 19).
F, H
300
200
100
0,05
t, мс
46
Рис. 19
Пользуясь графическим методом, определите:
1. Величину полного импульса, сообщенного мячу;
2. Скорость мяча после удара, считая, что до удара он находился в покое.
Задача 95
Сила взаимодействия шаров массой m  0,5 кг каждый при упругом
центральном соударении зависит от времени так, как показано на рисунке 20.
Используя график, определить: 1) изменение импульса каждого шара за
время взаимодействия; 2) среднюю силу взаимодействия шаров.
F, H
500
400
300
200
2
4
6
t, мс
Рис. 20
Задача 96
Два упругих шара движутся навстречу друг другу, причем скорость первого
удара в два раза меньше скорости второго шара, а его масса в два раза
больше массы второго шара. Считая удар шаров абсолютно упругим,
укажите верные утверждения из утверждений, приведенных ниже.
1. mV
1 1  m2V2  m1U1  m2U 2 ;
2. m1V1  m2V2  m1U1  m2U 2 ;
3. m1V1  m2V2  m1U1  m2U 2 ;
4. m1V1  m2V2  m1U1  m2U 2 ;
5. m1V1  m2V2  0 .
Здесь m1 , m2 - массы первого и второго тела, V1 , V2 - скорости первого и
второго шара до удара; U1 , U 2 - скорости первого и второго шара после
удара.
Задача 97
Движущийся шар массой m упруго соударяется с покоящимся шаром массой
2m . После удара шар массой m движется в противоположном направлении.
Во сколько раз изменилась скорость этого шара?
47
Задача 98
При центральном абсолютно упругом ударе движущееся тело массой m1
сталкивается с покоящимся шаром массой m2 . В результате этого удара
скорость первого тела уменьшается в n  1,5 раза. Определите отношение
m
масс тел 1 .
m2
Задача 99
Шар A движется навстречу шару B по горизонтальной поверхности со
скоростью V1  2 м/с. Масса шара A в два раза больше массы шара B .
Скорость шара B V2 в два раза больше скорости шара A . Найти скорости
шаров после упругого удара. Найти направление движения шаров после
удара. Удар считать центральным.
Задача 100
Шар A движется по горизонтальной поверхности со скоростью V1  1, 2 м/с и
догоняет шар B , движущийся в том же направлении, что и шар A , со
скоростью V2  0,6 м/с. Масса шара A в два раза больше массы шара B .
Определите скорости и направления движения шаров после упругого
столкновения.
Задача 101
Шар A движется по горизонтальной поверхности со скоростью V1  6 м/с и
сталкивается упруго с неподвижным шаром B . Масса шара A в два раза
больше массы шара B . Куда и с какой скоростью будут двигаться шары
после удара? Удар считать центральным.
Задача 102
Два тела массами 2 кг и 6 кг движутся навстречу друг другу со скоростями
2 м/с каждое. Определить модуль и направление скоростей этих тел после их
неупругого соударения.
Задача 103
В покоящийся шар массой m упруго ударяется шар массой
шар
массой
первоначальному
m
2
движется
направлению.
в
направлении,
Определите,
под
m
. После удара
2
перпендикулярном
каким углом к
m
первоначальному направлению движения шара массой
будет двигаться
2
шар массой m после удара.
48
Задача 104
В покоящийся шар массой m упруго ударяется шар массой
шар
массой
первоначальному
m
3
движется
направлению.
в
направлении,
Определите,
m
. После удара
3
перпендикулярном
под
каким углом к
m
первоначальному направлению движения шара массой
будет двигаться
3
шар массой m после удара.
Задача 105
Шар массой m  0,5 кг испытывает упругое соударение с другим шаром,
покоившимся до удара. После удара первый шар отлетает от него в
противоположную первоначальному движению сторону со скоростью,
равной одной трети начальной скорости. Чему равна масса второго шара?
Задача 106
Шар массой m1  1 кг испытывает абсолютно упругое столкновение с другим
шаром, который до удара находился в покое. После удара первый шар
1
движется со скоростью, равной первоначальной скорости, в ту же сторону.
4
Определите массу второго шара.
Задача 107
Тело массой m1  600 г, движущееся со скоростью V1 , налетает на
неподвижное тело и после упругого удара отскакивает от него под углом 900
V
к первоначальному направлению своего движения со скоростью V1  1 .
2
Определите массу второго тела.
Задача 108
Два тела движутся навстречу друг другу со скоростями V1  V2  1 м/с. После
столкновения шары движутся в противоположные стороны со скоростями
U1  U 2  0,5 м/с. Определите коэффициент восстановления шаров.
Задача 109
Стальной шар падает с высоты h1  1 м и после удара о стальную плиту
h2  90
подскакивает на высоту
см. Определите коэффициент
восстановления шара при ударе о плиту.
49
Задача 110
Свинцовый шар падает с высоты h1  1,5 м на стальную плиту и после удара
подскакивает на высоту h2  0,1 м. Определите коэффициент восстановления
шара при ударе.
Задача 111
Два стальных шара движутся по одной прямой в одном направлении.
Скорости шаров равны V1  1 м/с и V2  0,5 м/с, массы шаров равны m1  0, 2
кг и m2  0,1 кг. После столкновения первый шар не изменил направление
движения, но стал двигаться со скоростью U1  0,7 м/с. Определите
коэффициент восстановления шаров и изменение импульса каждого шара
при ударе.
Задача 112
Два шара движутся навстречу друг другу со скоростями V1  1 м/с и V2  0,5
м/с и сталкиваются. После столкновения шары движутся в одном
направлении со скоростями U1  0,6 м/с и U 2  0,1 м/с. Определите
коэффициент восстановления шаров.
Задача 113
Два шара движутся по одной прямой в одном направлении со скоростями
V1  1,5 м/с и V2  0,5 м/с и сталкиваются. После столкновения шары
движутся в том же направлении со скоростями U1  1, 2 м/с и U 2  1 м/с.
Определите коэффициент восстановления шаров.
Задача 114
Два шара движутся навстречу друг другу со скоростями V1  1 м/с и V2  0,5
м/с. После столкновения шары движутся в противоположные стороны со
скоростями U1  0,7 м/с и U 2  0, 2 м/с. Определите коэффициент
восстановления шаров.
Задача 115
Два стальных шара движутся по одной прямой в одну сторону со скоростями
V1  1 м/с и V2  0, 2 м/с. Первый шар догоняет второй шар и сталкивается с
ним. После столкновения первый шар движутся в обратную сторону со
скоростью U1  0,3 м/с, а второй шар продолжает двигаться в прежнем
U 2  0,5 м/с. Определите коэффициент
направлении со скоростью
восстановления шаров.
50
Задача 116
Шар массой m1 упруго сталкивается с покоящимся шаром массой m2  3m1 .
При этом скорость первого шара уменьшилась в два раза. Определите
отношение кинетических энергий шаров после удара.
Задача 117
Движущийся шар ударяет в неподвижный шар такой же массы, после чего
шары стали двигаться как одно целое. Какая часть механической энергии
перешла во внутреннюю энергию?
Задача 118
Два шара одинаковой массы m1  m2  1 кг сталкиваются друг с другом.
Коэффициент восстановления шаров при ударе k  0,5 . Считая удар
центральным, определите количество теплоты, выделившееся при ударе.
Скорость шаров перед ударом одинакова и равна V1  V2  1 м/с.
Задача 119
Ком мягкой глины массой m  0,2 кг ударяется о вертикальную стенку и
прилипает к ней. Определите импульс силы, полученной стенкой. И
количество теплоты, выделившееся при ударе. Скорость комка перед ударом
направлена перпендикулярно стенке и равна V  1,5 м/с.
Задача 120
Два глиняных шара движутся по одной прямой в одном направлении со
скоростями V1  0,5 м/с и V2  0, 2 м/с. Первый шар догоняет второй и не
упруго сталкивается с ним. Определите количество теплоты, которое
выделяется при столкновении. Массы шаров равны m1  0,5 кг и m2  0,3 кг.
Задача 121
Два глиняных шара движутся навстречу друг другу со скоростями V1  0,5 м/с
и V2  1 м/с. Массы шаров m1  0,3 кг и m2  0, 2 кг. Определите скорости
шаров после неупругого удара и вычислите количество теплоты, которое
выделится при ударе.
Задача 122
Шар A массой 100 г сталкивается не упруго с неподвижным шаром B
массой 200 г. Определите, с какой скоростью, и в каком направлении будут
двигаться шары после столкновения. Какая энергия выделится при ударе?
Скорость шара A до удара равна V1  0,6 м/с. Удар считать центральным.
51
Задача 123
Шар A массой m1  200 г движется по горизонтальной поверхности со
скоростью V1  0,6 м/с и догоняет шар B массой 0,4 кг, движущийся в том
же направлении со скоростью V2  0,3 м/с. Определите, с какой скоростью, и
в каком направлении будут двигаться шары после столкновения. Какая
энергия выделится при ударе? Удар считать центральным и неупругим.
Задача 124
Шар A массой m1  200 г движется навстречу шару B массой m2  400 г. по
горизонтальной поверхности. Скорость шара A равна V1  0,6 м/с, а
скорость шара B равна V2  0,3 м/с. Определите, с какой скоростью, и в
каком направлении будут двигаться шары после столкновения. Какая энергия
выделится при ударе? Удар считать центральным и неупругим.
Задача 125
Два упругих шарика подвешены на тонких нитях так, что их центры масс
находятся на одной высоте, и шарики соприкасаются. Длины нитей
одинаковы и равны l  20 см. Массы шариков равны m1  10 г и m2  20 г.
Шарик массой m1 отклонили от вертикали на угол   600 и отпустили без
начальной скорости. Определите максимальные углы отклонения шариков от
вертикали после абсолютно упругого соударения.
Задача 126
m1
4
подвешены на нитях в одной точке. Свинцовый шар отклоняют от вертикали
так, что он поднимается на высоту H  20 см и отпускают без начальной
скорости. После соударения он поднимается на высоту h  10 см. считая удар
центральным, определить, какое количество теплоты выделилось при ударе.
Два шара стальной шар массой m1  200 г и свинцовый шар массой m2 
Задача 127
Две частицы массами m1  105 кг и m2  2m1 . Импульсы частиц равны
P
P1  6 103 кг м/с и P2  1 . Частицы движутся по взаимно
2
перпендикулярным направлениям. После соударения частица обмениваются
импульсами. Определите потери механической энергии при соударении.
Задача 128
На двух шнурах одинаковой длины l  1 м подвешены два шара массами
m1  1 кг и m2  0,5 кг. Шары соприкасаются друг с другом. Шар большей
массы отклонили от вертикали на угол   600 и отпустили без начальной
52
скорости. Считая удар шаров центральным и абсолютно неупругим,
определить энергию, израсходованную на деформацию шаров при ударе.
Задача 129
На двух шнурах одинаковой длины l  1 м подвешены два шара массами
m1  1 кг и m2  0,5 кг. Шары соприкасаются друг с другом. Шар меньшей
массы отклонили от вертикали на угол   600 и отпустили без начальной
скорости. Считая удар шаров центральным и абсолютно неупругим,
определить энергию, израсходованную на деформацию шаров при ударе.
Задача 130
Шары A и B подвешены на нитях одинаковой длины l  1 м так, что они
соприкасаются. В состоянии покоя центры шаров лежат на горизонтали. Шар
A отклонили от вертикали на угол   100 и отпустили без начальной
скорости. На какую высоту поднимутся шары после их неупругого
соударения, если масса шара A в два раза больше массы шара B ?
Задача 131
Два шара A и B подвешены на нитях одинаковой длины l  1 м так, что они
в состоянии покоя соприкасаются, а центры шаров лежат на одной
горизонтали. Шар B отклонили от вертикали на угол   100 и отпустили без
начальной скорости. На какую высоту поднимутся шары после их
неупругого соударения, если масса шара A в два раза больше массы шара
B?
Задача 132
Два шара A и B подвешены на нитях одинаковой длины l  1 м так, что они
в состоянии покоя соприкасаются, а центры шаров лежат на одной
горизонтали. Шар B отклонили от вертикали на угол   100 и отпустили без
начальной скорости. На какую высоту поднимется каждый шар после их
упругого соударения, если масса шара A в два раза больше массы шара B ?
Задача 133
Два шара A и B подвешены на нитях одинаковой длины l  1 м так, что они
в состоянии покоя соприкасаются, а центры шаров лежат на одной
горизонтали. Шар A отклонили от вертикали на угол   100 и отпустили без
начальной скорости. На какую высоту поднимется каждый шар после их
упругого соударения, если масса шара A в два раза меньше массы шара B ?
Задача 134
Два упругих шарика подвешены на тонких нитях рядом так, что их центры
масс находятся на одной высоте и шарики соприкасаются (Рис. 21). Длина
нити, на которой подвешен первый шарик, равна l1  10 см, а длина нити, на
53
которой подвешен второй шарик, равна l2  5 см. Массы шариков одинаковы
и равны 20 г. Первый шарик отклоняют от вертикали на угол   600 и
отпускают без начальной скорости. Определите углы отклонения шариков от
вертикали после абсолютно упругого удара.
1
2
Рис. 21
Задача 135
Два упругих шарика подвешены на тонких нитях рядом так, что их центры
масс находятся на одной высоте и шарики соприкасаются (Рис. 21). Длина
нити, на которой подвешен первый шарик, равна l1  10 см, а длина нити, на
которой подвешен второй шарик, равна l2  5 см. Массы шариков одинаковы
и равны 20 г. Второй шарик отклоняют от вертикали на угол   600 и
отпускают без начальной скорости. Определите углы отклонения шариков от
вертикали после абсолютно упругого удара.
Задача 136
Два шарика подвешены на тонких нитях рядом так, что их центры масс
находятся на одной высоте и шарики соприкасаются (Рис. 21). Длина нити,
на которой подвешен первый шарик, равна l1  10 см, а длина нити, на
которой подвешен второй шарик, равна l2  5 см. Массы шариков одинаковы
и равны 20 г. Первый шарик отклоняют от вертикали на угол   600 и
отпускают без начальной скорости. Определите угол отклонения шариков от
вертикали после абсолютно неупругого удара.
Задача 137
Два упругих шарика подвешены на тонких нитях рядом так, что их центры
масс находятся на одной высоте и шарики соприкасаются (Рис. 21). Длина
нити, на которой подвешен первый шарик, равна l1  1 м, а длина нити, на
которой подвешен второй шарик, равна l2  0,5 м. Массы шариков
одинаковы и равны 0,01 кг. Второй шарик отклоняют от вертикали на угол
54
  600 и отпускают без начальной скорости. Определите углы отклонения
шариков от вертикали после абсолютно упругого удара.
Задача 138
Стальной шар массой m  0,1 кг падает с высоты h1  2,5 м на стальную
плиту и, ударившись о нее, подскакивает на высоту h2  h1 . Из приведенный
ниже утверждений укажите неверное утверждение:
1. Удар шара о плиту является абсолютно упругим;
2. Коэффициент восстановления шара при ударе равен 1;
3. Импульс силы, полученной плитой за время удара, равен 0,7 Нс;
4. Импульс шара при ударе изменился на 1,4 кгм/с;
5. Импульс силы, полученный шаром за время удара, равен 1,4 Нс.
Задача 139
Два шара: пластилиновый массой m1  0,1 кг и стальной массой m2  0,1 кг
движутся по одной прямой навстречу друг другу. Скорости шаров равны
соответственно V1  5 м/с и V2  10 м/с и шары сталкиваются не упруго.
Какое из приведенных ниже утверждений является неверным?
1. Коэффициент восстановления шаров при ударе равен нулю;
2. Скорость обоих шаров после удара одинакова и равна 2,5 м/с;
3. Относительная скорость шаров до удара равна 5 м/с;
4. Закон сохранения импульса в проекции на прямую линию, по которой
движутся шары, для данного взаимодействия имеет вид:
mV
1 1  m2V2   m1  m2 V ;
5. Во внутреннюю энергию перешло 0,9 первоначальной механической
энергии шаров.
Задача 140
Два стальных шара массой m1  0,1 кг m2  0,1 кг движутся по одной прямой
в одну сторону. Скорости шаров равны соответственно V1  2 м/с и V2  1 м/с
и шары сталкиваются абсолютно упруго. Какое из приведенных ниже
утверждений является верными?
1. Относительная скорость шаров по абсолютной величине до удара и
после удара одинакова и равна 1 м/с;
2. После удара скорости первого и второго шара равны соответственно
U1  1 м/с и U 2  2 м/с;
3. Коэффициент восстановления шаров при ударе равен 1;
4. Закон сохранения импульса в проекции на прямую линию, по которой
движутся шары, для данного взаимодействия имеет вид:
m1V1  m2V2  m1U1  m2U 2 ;
55
5. Так как удар упругий, то выполняется закон сохранения механической
m1V12 m2V22 m1U12 m2U 22



энергии:
.
2
2
2
2
Задача 141
Два шара: пластилиновый массой m1  0, 2 кг и стальной массой m2  0,1 кг
движутся по одной прямой в одном направлении. Скорости шаров равны
соответственно V1  0,5 м/с и V2  1 м/с, и шары сталкиваются не упруго.
Какое из приведенных ниже утверждений является неверным?
1. Закон сохранения импульса в проекции на прямую линию, по которой
движутся шары, для данного взаимодействия имеет вид:
mV
1 1  m2V2   m1  m2 V ;
2. Коэффициент восстановления шаров при ударе равен нулю, так как
удар абсолютно неупругий;
3. Скорость обоих шаров после удара одинакова и равна 2/3 м/с;
4. Импульс силы, полученный каждым шаром за время удара, равен 1/30
Нс;
5. Закон сохранения энергии выполняется в виде:
2
m1V12 m2V22  m1  m2 V
.


2
2
2
6. Динамика вращательного движения тела вокруг неподвижной оси
Задача 142
Что необходимо знать для определения направления и величины вектора
углового ускорения тела при его вращении вокруг неподвижной оси? Указать
правильные ответы.
11.Ориентацию оси вращения;
12.Направление вектора силы;
13.Направление и величину момента внешней силы;
14.Момент инерции тела;
15.Массу тела.
Задача 143
Что необходимо знать для определения направления момента силы? Указать
правильные ответы.
1. Величину действующей силы;
2. Точку приложения силы;
3. Направление действующей силы;
4. Радиус-вектор точки, к которой приложена сила;
5. Положение оси вращения.
56
Задача 144
На рисунках (Рис. 22) приведены направления сил и моментов этих сил для
заданной материальной точки A . OO - ось вращения. Укажите, на каких
рисунках направление момента силы соответствуют направлению силы и
расположению точки A относительно оси вращения.
O
1
O
2
A
A
O
O
57
3
O
4
O
O
A
A
O
5
A
O
O
Рис. 22
Задача 145
На рисунке (Рис. 23) изображен диск, вращающийся вокруг оси OO с
некоторой угловой скоростью  . В точке A к диску приложена сила F ,
составляющая угол  с радиус-вектором r точки, в которой приложена сила.
Укажите правильные утверждения об угловой скорости вращения диска:
1. Если угол  равен нулю, то скорость вращения диска не изменяется;
2. Если вектор силы лежит в плоскости, перпендикулярной плоскости
диска, и в той же плоскости лежит радиус-вектор точки, то при любом
угле  скорость вращения диска не изменяется;
3. Скорость вращения диска возрастает, если вектор силы лежит в
плоскости диска и угол между радиус-вектором точки и вектором силы
не равен нулю;
4. Наибольшее изменение скорости вращения диска будет в случае, когда
вектор силы лежит в плоскости диска и перпендикулярен радиусвектору точки;
5. Скорость вращения диска не изменится, если вектор силы параллелен
оси вращения
58
O
A
O
Рис. 23
Задача 146
Угловая скорость вращения цилиндра вокруг неподвижной оси,
совпадающей с осью цилиндра, возросла. Вследствие чего это произошло?
Укажите наиболее правильные ответы.
1. К цилиндру приложена внешняя сила;
2. Угловое ускорение цилиндра, возникающее под действием внешней
силы, совпадает с направлением угловой скорости;
3. На цилиндр действовал момент внешних сил;
4. Если при наблюдении сверху цилиндр вращается по часовой стрелке, а
его скорость возросла, то к телу приложена внешняя сила, момент
которой направлен вниз;
5. Изменился момент инерции цилиндра.
Задача 147
На рисунках (Рис. 24) приведены направления силы, приложенной к телу,
радиус-вектор точки A , к которой она приложена, и направление углового
ускорения. Укажите рисунки, на которых направление углового ускорения
соответствуют положению точки и направлению силы. OO - ось вращения
тела.
59
1
O
O
2
A
A
O
O
O
O
3
4
A
A
O
O
5
A
O
O
Рис. 24
Задача 148
На рисунке (Рис. 25) представлен диск, вращающийся с некоторой угловой
скоростью  . После действия на диск некоторой силы F , направленной под
углом  к радиусу диска, скорость диска осталась прежней. Укажите
неправильные ответы, представленные для объяснения этой ситуации.
1. Вектор силы направлен параллельно оси вращения;
60
2. Вектор силы перпендикулярен плоскости диска;
3. Вектор силы и радиус-вектор точки на краю диска, к которой
приложена сила, лежат в плоскости диска;
4. Вектор силы параллелен радиус-вектору точки;
5. Вектор силы параллелен плоскости диска.
O
O
Рис. 25
Задача 149
К диску массой 20 кг и радиусом 0,3 м, вращающемуся вокруг неподвижной
оси, проходящей через центр диска перпендикулярно его плоскости,
приложен вращающий момент 3,6 Нм. Определить угловое ускорение диска.
Задача 150
Однородный стержень длиной 1 м и массой 0,6 кг вращается в вертикальной
плоскости вокруг горизонтальной оси, проходящей через середину стержня.
С каким угловым ускорением вращается стержень, если вращающий момент
равен 1,5 Нм?
Задача 151
На маховое колесо радиусом 2 м действует вращающий момент 20 Нм.
Какова масса колеса, если угловое ускорение его вращения вокруг оси,
проходящей через его центр перпендикулярно плоскости кольца, равно 4 с -2?
Массу колеса считать равномерно распределенной по ободу.
Задача 152
Диск диаметром 20 см и массой 1 кг катится по горизонтальной поверхности
с линейной скоростью 2 м/с. Найти полную кинетическую энергию диска.
61
Задача 153
Колесо массой 5 кг катится по горизонтальной поверхности с линейной
скоростью 0,5 м/с. Определить полную кинетическую энергию колеса,
считая, что его масса равномерно распределена по ободу.
Задача 154
Шар массой 1 кг катится по горизонтальной поверхности с линейной
скоростью 1,5 м/с. Определить полную кинетическую энергию шара.
Задача 155
По горизонтальной поверхности с одинаковой линейной скоростью V
катятся обруч и шар, имеющие одинаковую массу m . Найти отношение их
кинетических энергий.
Задача 156
По горизонтальной поверхности с одинаковой линейной скоростью V
катятся сплошной цилиндр и обруч, имеющие одинаковую массу m . Найти
отношение их кинетических энергий.
Задача 157
Два диска одинаковой массы вращаются под действием равных вращающих
моментов. Во сколько раз отличаются угловые ускорения дисков, если
радиус второго диска в два раза больше радиуса первого диска?
Задача 158
Диск массой 100 кг и радиусом 0,1 м вращается вокруг неподвижной оси,
проходящей через центр диска перпендикулярно его плоскости. Какой
вращающий момент надо приложить к диску, чтобы сообщить ему угловое
1
ускорение 4  102 2 ?
c
Задача 159
Диск радиусом 50 см и массой 20 кг вращается с угловой скоростью 2 с-1
вокруг оси, проходящей через его центр перпендикулярно плоскости диска.
Какую работу необходимо совершить, чтобы остановить его вращение?
Задача 160
Какую работу нужно совершить, чтобы из состояния покоя раскрутить
маховик до частоты вращения 120 об/мин. Массу маховика 400 кг считать
равномерно распределенной по ободу, диаметр которого 1,5 м? трением
пренебречь.
62
Задача 161
Шар массой 2 кг катится без скольжения, ударяется о стенку и отскакивает от
нее. Скорость шара до удара равна 15 см/с, а после удара 10 см/с. Определите
количество теплоты, выделившееся при ударе.
Задача 162
На барабан намотан шнур, к концу которого привязан груз массой 3 кг.
Масса барабана равна 12 кг. Найти ускорение груза, считая барабан
сплошным однородным цилиндром. Трением пренебречь.
Задача 163
Найти ускорение центра шара, скатывающегося без скольжения по
наклонной плоскости, наклоненной к горизонту под углом 45 0.
Задача 164
Обруч массой 0,25 кг и радиусом 10 см соединен с горизонтальной осью
вращения тонким стержнем длиной 0,5 м и массой 0,3 кг. Плоскость обруча
перпендикулярна оси вращения. Стержень отвели на угол 900 и отпустили
без начальной скорости. Найти скорость центра обруча в момент
прохождения им положения равновесия.
Задача 165
Массивный цилиндр радиусом 15 см может вращаться вокруг
горизонтальной оси, совпадающей с осью цилиндра. На цилиндр навит
тонкий шнур, к концу которого привязан груз массой 1,5 кг. Груз опускается
вниз, разматывая шнур. Найти массу цилиндра, если груз за первую секунду
своего движения прошел расстояние 1 м.
Задача 166
Шар и цилиндр одинаковой массы и одинакового радиуса начинают
одновременно скатываться без скольжения с наклонной плоскости. Какое из
тел быстрее достигнет основания наклонной плоскости? Будет ли равно
отношение скоростей центров этих тел у основания плоскости отношению
времен движения?
Задача 167
Шар массой 0,5 кг и радиусом 10 см соединен с горизонтальной осью
вращения тонким стержнем длиной 0,8 м и массой 0,1 кг стержень отклонили
на угол 900 и отпустили без начальной скорости. Найти скорость центра шара
в момент прохождения им положения равновесия.
Задача 168
Массивный цилиндр массой 35 кг и радиусом 10 см может вращаться вокруг
горизонтальной оси, совпадающей с осью цилиндра. На цилиндр навит
63
тонкий шнур, к концу которого привязан груз массой 1,5 кг. Груз движется
вниз, разматывая шнур. С каким ускорением движется груз? Массой шнура и
трением пренебречь.
Задача 169
Найдите ускорение центра однородного диска, скатывающегося без
скольжения по плоскости, наклоненной под углом 450 к горизонту.
Задача 170
Массивный цилиндр массой 40 кг и радиусом 10 см может вращаться вокруг
горизонтальной оси, совпадающей с осью цилиндра. На цилиндр навит
длинный тонкий шнур. Шнур разматывают, прикладывая постоянную силу.
Определить величину этой силы, если за 10 с цилиндр раскрутился до
скорости 30 об/мин.
Задача 171
Диск массой m и радиусом R вращается вокруг своей оси с угловой
скоростью  . Под действием внешней силы диск останавливается. Чему
равна работа внешней силы?
Задача 172
На барабан массой 8 кг намотан шнур, к концу которого привязан груз
массой 2 кг. Найти ускорение груза. Барабан считать однородным
цилиндром. Трением пренебречь.
Задача 173
Диск массой 3 кг катится без скольжения по горизонтальной плоскости со
скоростью 4 м/с. Определить кинетическую энергию диска.
Задача 174
Обруч и диск одинаковой массы катятся без скольжения с одной и той же
скоростью. Кинетическая энергия обруча равна 39,2 Дж. Найти
кинетическую энергию диска.
Задача 175
Карандаш длиной 12 см, поставленный вертикально, падает на стол. Какую
угловую и линейную скорость будет иметь в конце падения середина
карандаша? Считать, что трение настолько велико, что нижний конец
карандаша не проскальзывает.
Задача 176
Тонкий прямой стержень длиной 1,5 м прикреплен к горизонтальной оси,
проходящей через его конец. Стержень отклонили на угол 600 от положения
равновесия и отпустили без начальной скорости. Определить линейную
64
скорость нижнего конца стержня в момент прохождения положения
равновесия.
Задача 177
Обруч катится по горизонтальной дороге со скоростью 4 м/с. На какое
максимальное расстояние обруч может вкатиться на гору с уклоном 10 м на
каждые 100 м пути?
Задача 178
Во сколько раз отличаются времена скатывания обруча и диска, имеющих
одинаковую массу и одинаковый радиус, с одной наклонной плоскости?
Начальная скорость тел равна нулю.
Задача 179
Найти линейные скорости движения центров шара, диска и обруча,
скатывающихся без скольжения с наклонной плоскости. Высота наклонной
плоскости равна 0,7 м, начальная скорость всех тел равна нулю. Сравнить
найденные скорости со скоростью тела, соскальзывающего с этой наклонной
плоскости при отсутствии трения с нулевой начальной скоростью.
Задача 180
Однородному цилиндру сообщают начальный импульс, в результате чего он
начинает катиться без скольжения вверх по наклонной плоскости со
скоростью 5 м/с. Плоскость образует с горизонтом угол 200. На какую высоту
поднимется цилиндр? Какую скорость будет иметь цилиндр в момент
возвращения в исходное состояние?
Задача 181
Расположенный горизонтально однородный круглый цилиндр массой 10 кг
вращается без трения вокруг своей оси под действием груза массой 1 кг,
прикрепленного к легкой нерастяжимой нити, намотанной на цилиндр.
Найти кинетическую энергию системы через 3,53 с после начала движения.
Задача 182
Диск весом P катится без скольжения по горизонтальной плоскости со
скоростью V . Найти кинетическую энергию диска.
Задача 183
К ободу однородного диска радиусом 0,3 м с осью вращения, проходящей
через центр диска перпендикулярно плоскости его основания, приложена
постоянная касательная сила, равная 98,1 Н. В процессе вращения в оси
диска действует момент сил трения, равный 5 Нм. Определить массу диска,
если он вращается с угловым ускорением 100 рад/с.
65
Задача 184
Маховое колесо, имеющее момент инерции 245 кгм2, вращается, делая 20
об/с. Через одну минуту после того, как на колесо перестал действовать
вращающий момент, оно остановилось. Определить: 1) момент сил трения,
действующий на колесо; 2) число оборотов, которое сделало колесо до
полной остановки после прекращения действия вращающего момента.
Задача 185
Диск и шар одинаковой массы и радиуса вкатываются на наклонную
плоскость с одинаковой начальной скоростью. Найти отношение
максимальных высот подъема этих тел.
Задача 186
Стержень длиной 0,6 м и массой 0,1 кг может вращаться без трения вокруг
горизонтальной оси, проходящей через его конец. К нижнему концу стержня
прикреплен шар массой 0,2 кг и радиусом 0,1 м. Стержень отклонили на угол
900 от вертикали и отпустили без начальной скорости. Определить
максимальную угловую скорость стержня.
Задача 187
Однородный тонкий стержень длиной 20 см вертикально стоит на
горизонтальной поверхности. Утратив равновесие, стержень начинает падать.
Определить максимальную линейную скорость верхнего конца стержня.
Начальная скорость стержня равна нулю.
Задача 188
Кинетическая энергия вращающегося маховика равна 3 кДж. Под действием
постоянного тормозящего момента маховик начал вращаться равно
замедлено, и, сделав 60 оборотов, остановился. Определить тормозящий
момент.
Задача 189
На тяжелый барабан, вращающийся вокруг горизонтальной оси, намотан
легкий гибкий шнур. По шнуру лезет вверх обезьяна массы M . Определить
ускорение обезьяны относительно шнура, если ее скорость относительно
земли постоянна. Момент инерции барабана равен I , его радиус R .
Задача 190
На сплошной цилиндр массой m намотана тонкая невесомая нить. Другой
конец нити прикреплен к потолку лифта, движущегося вверх с ускорением
a . Найти ускорение цилиндра относительно лифта и силу натяжения нити.
66
Задача 191
Какую скорость приобретают сплошной и полый цилиндр, скатившись без
скольжения с наклонной плоскости высотой 1,5 м? Массы цилиндров и их
радиусы одинаковы. Какую скорость имели бы эти цилиндры, если бы они
соскальзывали без трения с наклонной плоскости?
Задача 192
Обруч и сплошной цилиндр одинаковой массы и диаметра поднимаются
вверх по наклонной плоскости и достигают одинаковой высоты. Определите
отношение их линейных скоростей в начале подъема.
Задача 193
Какую скорость приобретают сплошной и полый шары, скатившись без
скольжения с наклонной плоскости высотой 1 м? Массы шаров и их радиусы
одинаковы. Какую скорость имели бы эти шары, если бы они соскальзывали
без трения с наклонной плоскости?
Задача 194
Кинетическая энергия вращающегося маховика 1 кДж. Под действием
постоянного тормозящего момента маховик начал вращаться замедленно, и
сделав 80 оборотов, остановился. Определить тормозящий момент, считая
ускорение постоянным по величине.
Задача 195
Маховое колесо начинает вращаться с постоянным угловым ускорение 0,5
рад/с2 и через 15 с после начала движения приобретает момент импульса 73,5
кгм2/с. Определите кинетическую энергию колеса через 20 с после начала
движения.
Задача 196
Вращающийся с угловой скоростью 0 сплошной однородный цилиндр
радиусом r начинает без начальной поступательной скорости подниматься
по наклонной плоскости, составляющей угол  с горизонтом. Определить
время, в течение которого цилиндр достигнет наибольшей высоты. Трение не
учитывать.
Задача 197
Однородный стержень длиной 25 см подвешен на горизонтальной оси,
проходящей через верхний конец стержня. Какую минимальную скорость
необходимо сообщить нижнему концу стержня, чтобы он сделал полный
оборот вокруг оси?
67
Задача 198
Однородный стержень длиной 65 см подвешен на горизонтальной оси,
проходящей через верхний конец стержня. Какую минимальную скорость
необходимо сообщить нижнему концу стержня, чтобы он сделал полный
оборот вокруг оси?
Задача 199
Шар скатывается без скольжения с наклонной плоскости, составляющей угол
300 с горизонтом. Определить ускорение центра тяжести шара.
Задача 200
Сплошной цилиндр массой 20 кг и радиусом 120 мм вращается, совершая 600
об/мин. С какой силой нужно прижать к нему тормозную колодку, чтобы он
остановился через 3 с, если коэффициент трения между колодкой и
цилиндром равен 0,1?
Задача 201
На покоящийся маховик, момент инерции которого 4,5 кгм 2, начал
действовать вращающий момент 12,5 Нм. Сколько оборотов сделает маховик
к тому моменту, когда его угловая скорость достигнет величины,
соответствующей 100 об/мин?
Задача 202
Маховик, момент инерции которого равен 40 кгм2, начал вращаться
равноускорено из состояния покоя под действием момента силы 20 Нм.
Равноускоренное вращение продолжалось 15 с. Определить кинетическую
энергию, приобретенную маховиком.
Задача 203
Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по
наклонной плоскости с углом наклона 300 к горизонту. Начальная скорость
диска равна 7 м/с. Скорость направлена параллельно наклонной плоскости?
Задача 204
Твердое тело с моментом инерции I вращается с угловым ускорением  и
мгновенной угловой скоростью  вокруг своей оси. Определить мощность,
сообщаемую телу.
Задача 205
Стержень длиной 1,5 м и массой 10 кг может вращаться вокруг неподвижной
оси, проходящей через верхний конец. В середину стержня ударяет пуля
массой 10 г, летящая в горизонтальном направлении со скоростью 500 м/с, и
застревает в нем. На какой угол отклонится стержень после удара?
68
Задача 206
Концы невесомой нерастяжимой нити намотаны на два одинаковых
однородных сплошных диска, один из которых имеет фиксированную ось
вращения (Рис. 26). Второй диск, вращаясь, движется вниз. Найдите
ускорение центра масс второго диска.
Рис. 26
Рис. 27
Рис. 29
Рис. 28
69
Задача 207
На сплошной однородный диск с фиксированной осью вращения намотана
невесомая нерастяжимая нить (Рис. 27). К концу нити прикреплен груз
массой 2 кг. Груз движется вниз, разматывая нить. Найдите ускорение груза,
если масса диска 3 кг.
Задача 208
Через сплошной однородный диск с фиксированной осью вращения (Рис. 28)
перекинута невесомая нерастяжимая нить. К концам нити перекинуты грузы
массами 2 кг и 3 кг, которые при своем движении заставляют диск вращаться
без проскальзывания. Найти ускорение грузов, если масса диска 3 кг.
Задача 209
На сплошной однородный диск намотана невесомая нерастяжимая нить,
второй конец которой закреплен (Рис. 29). С каким ускорением будет
опускаться диск, если его предоставить самому себе?
Задача 210
Вентилятор вращается с частотой 15 с-1. После выключения вентилятор,
вращаясь равно замедлено, сделал до остановки 75 оборотов. Работа сил
торможения 44,4 Дж. Определить момент сил торможения, считая его
постоянным.
Задача 211
Рамка может вращаться вокруг проходящей через ее центр инерции
вертикальной оси OZ . В рамке симметрично относительно оси OZ на
расстояниях L  0,2 м от оси укреплены вертикальные оси двух одинаковых
дисков массами 1 кг каждый (Рис. 30). Момент инерции рамки относительно
оси OZ равен 0,02 кгм2, момент инерции каждого диска относительно
собственной оси равен 0,01 кгм2. Вначале система находится в покое. Затем
диски начинают вращаться в одну сторону с одинаковой угловой скоростью
10 об/с относительно рамки. Определить угловую скорость рамки.
70
Z
m
m
L
L
O
Рис. 30
Задача 212
Колесо диаметром 0,1 м насажено на горизонтальную ось. Оно катится по
горизонтальной плоскости без скольжения вокруг вертикальной оси (Рис.
31). Колесо описывает окружность радиусом 0,2 м. Центр колеса движется со
скоростью 0,1 м/с. Найти значение результирующей угловой скорости колеса
и угол ее наклона к вертикали.
O
D
R
O
Рис. 31
Задача 213
На горизонтальном столе лежит тело массой 150 г, связанное нитью,
переброшенной через блок массой 100 г, с грузом массой 200 г. (Рис. 32).
Блок представляет собой однородный сплошной диск радиусом 5 см. Считая,
что в системе отсутствуют силы трения, найти ускорение тел и силы
натяжения нити
71
Рис. 32
Задача 214
Для машины Атвуда (Рис. 33) ускорение движения грузов определяется
m  m2
выражением a  1
g . Эта формула получена без учета вращения блока.
m1  m2
Как изменится значение ускорения, если учесть вращение блока, считая его
сплошным однородным диском? Рассчитать ускорение и натяжение нитей,
если m1  200 г, m2  100 г, а масса блока mбл  50 г. Радиус блока 10 см.
m,бл
R
m2
m1
Рис. 33
Задача 215
Человек массой 60 кг стоит на неподвижной круглой платформе на
расстоянии 60 см от оси платформы. Найти, с какой линейной скоростью
должен двигаться человек по окружности, чтобы платформа начала
вращаться, делая 10 об/мин. Масса платформы 100 кг, а ее диаметр 2 м.
72
Задача 216
Найти кинетическую энергию велосипедиста, который едет со скоростью 10
м/с. Масса велосипедиста с велосипедом 100 кг, масса каждого колеса 3 кг.
Колеса велосипеда считать обручами с диаметром 50 см. Какой путь проедет
велосипедист, не вращая педалями, при коэффициенте трения колес о дорогу
равном 0,1?
Задача 217
Масса велосипедиста с велосипедом равна 80 кг. Он движется со скоростью
12 м/с. Определить, какую энергию затрачивает велосипедист, если потери
энергии на трение составляют 10%. Колеса считать обручами массой 3 кг.
Задача 218
Вытащенное из колодца ведро с водой уронили, и оно стало опускаться вниз,
раскручивая ворот. Трение в подшипниках ворота создает постоянный
тормозящий момент 0,1 Нм. Масса ведра с водой 10 кг, масса ворота 20 кг,
радиус ворота 10 см. Расстояние от края сруба до поверхности воды в
колодце 10 м. Определить: 1) через какое время ведро коснется воды в
колодце; 2) какую скорость будет иметь ведро в конце падения; 3) какую
работу совершают силы трения за время падения ведра. Ворот считать
однородным цилиндром.
Задача 219
На какую высоту поднимутся шары центробежного регулятора, если он
делает 75 об/мин? Длина подвеса 0,6 м. (Рис. 34)
h
Рис. 34
Задача 220
Два резиновых диска с шероховатой поверхностью вращаются вокруг одной
и той же оси, совпадающей с осями симметрии дисков. Плоскости дисков
параллельны и расположены горизонтально. У одного диска момент инерции
0,1 кгм2 и угловая скорость 10 рад/с, а у другого момент инерции 0,2 кгм2 и
73
угловая скорость 5 рад/с. Определить угловую скорость и изменение
кинетической энергии системы из двух дисков при падении верхнего диска
на нижний диск и его соединении с нижним диском без проскальзывания.
Задача 221
Диск катится в течение 5 с и останавливается, пройдя расстояние 2м.
Определить коэффициент трения.
Задача 222
С какой скоростью должен въехать велосипедист в нижнюю точку «мертвой
петли» радиусом 4 м, чтобы не сорваться вниз в верхней точке петли? Масса
велосипедиста с велосипедом равна 80 кг, масса обоих колес 6 кг. Трением
пренебречь. Колеса считать обручами.
Задача 223
Два маховика в виде дисков радиусами 0,2 м и массой 10 кг каждый были
раскручены до угловой скорости 480 об/мин и предоставлены самим себе.
Под действием трения в подшипниках валов первый маховик остановился
через 80 с, а второй до полной остановки сделал 240 оборотов. Определить
моменты сил трения в подшипниках валов.
Задача 224
С наклонной плоскости скатывается без скольжения однородный диск
массой 475 г. Найти ускорение диска, если угол наклона плоскости к
горизонту равен 300.
Задача 225
Столб высотой 4 м и массой 25 кг подпиливают у основания. Считая столб
тонким и однородным, определить изменение кинетической и потенциальной
энергии столба при падении на землю, а также скорость падения его верхнего
конца.
Задача 226
Платформа в виде диска массой 10 кг и радиусом 2 м стоит на полу и
вращается, делая 10 об/с. В центре платформы стоит человек массой 60 кг.
Какую линейную скорость относительно пола будет иметь человек, если он
перейдет на край платформы? Человека считать точечным телом.
Задача 227
Металлическая цепочка длиной 60 см, концы которой соединены, висит на
диске. Диск вращается, делая 60 об/с. Определить силу натяжения цепочки,
если ее масса 40 г.
74
Задача 228
Однородный шар радиусом 20 см скатывается без начальной скорости, без
скольжения с наклонной плоскости, составляющей угол 300 с горизонтом.
Угловая скорость вращения шара 10 рад/с. Найти время, в течение которого
угловая скорость увеличится в 2 раза.
75
7 Момент инерции
Задача 229
На рисунке представлена система из четырех тел массой m (Рис. 35). Тела
можно считать материальными точками. Укажите номер формулы, по
которой определяется момент инерции системы тел относительно оси OO1 .
O
2R
2
R
R
R
1.
2.
3.
4.
I
I
I
I
 20mR 2 ;
 36mR 2 ;
 24mR 2 ;
 56mR 2
O1
Рис. 35
Задача 230
Какая из систем материальных точек имеет момент инерции относительно
оси OO1 , равный I  56mR 2 (Рис. 36)? Здесь m - масса материальных точек.
O
1.
2R
R
R
O
2.
2R
R
4.
O
2R
2R
O1
O1
3.
2R
R
2R
2R
O
2R
2R
O1
2R
O1
O
5.
2R
2R
2R
2R
Рис. 36
O1
76
Задача 231
На каком из рисунков (Рис. 37), изображенных ниже, момент инерции
системы материальных точек массой m относительно оси OO1 максимален?
O
1.
R
2.
R
2R
2R
O
2R
2R
2R
O1
O1
O
3.
O
4.
2R
2R
2R
2R
R
R
O1
2R
O1
O
5.
3R
R
2R
O1
Рис. 37
Задача 232
На каком из рисунков (Рис.38), представленных ниже, момент инерции
системы, состоящей из точечных грузов массой m , относительно оси OO1
минимален?
O
1.
2R
R
R
O1
2.
2R
R
O
R
O1
2R
2R
77
3.
O
2R
2R
4.
2R
O
2R
O1
2R
2R
O1
Рис. 38
Задача 233
Сколько верных утверждений приведено ниже. Укажите номера верных
утверждений.
1. Момент инерции тела не зависит от момента силы, действующей на
него;
2. Момент инерции тела зависит от его массы;
3. Момент инерции тела зависит от размеров и геометрической формы
тела;
4. Момент инерции тела характеризует инертность тела при
вращательном движении;
5. Момент инерции тела зависит от положения оси вращения
относительно центра масс тела.
Задача 234
На рисунке (Рис. 39) представлены различные положения сплошного
цилиндра относительно произвольной оси вращения O O  . Масса цилиндров
равна m , радиус цилиндров равен R . Указать номер рисунка, на котором
изображен цилиндр, момент инерции которого относительно оси O O  ,
равен:
1. I  0,75mR2 ; 2. I  4,5mR2 ; 3. I  2,7mR2 ; 4. I  1,5mR2
78
O
O
1
O
R
2
O
O1
O1
O
3
O
4
O
R
O1
O1
O
O
5
O
O1
Рис. 39
O
79
Задача 235
Плотность материала, из которого изготовлен стержень длиной l ,
равномерно возрастает от значения  0 на одном его конце до 2  0 на другом
конце (Рис.40). 1. Определить момент инерции стержня относительно оси
вращения, перпендикулярной стержню и проходящей через его
геометрический центр; 2. Вычислить момент инерции для стержня длиной
l  1 м и массой m  1 кг;
3. Определить момент инерции стержня относительно оси, проходящий через
его конец;
4. Вычислить момент инерции стержня длиной l  0,5 м и массой m  0,4 кг
относительно оси, проходящей через его конец
O1
O1
O
O
Рис. 40
Задача 236
На рисунках (Рис. 41) представлены различные положения стержня длиной l
и массой m . Ось OO проходит через середину стержня. На рисунках задано
положение оси O1O1 . Определить:
1. На каком рисунке момент инерции стержня относительно оси O1O1
минимален?
2. На каком рисунке момент инерции стержня относительно оси O1O1
максимален?
3. На каком рисунке момент инерции стержня относительно оси O1O1
ml 2
равен
?
3
4. На каком рисунке момент инерции стержня относительно оси O1O1
7ml 2
равен
?
36
5. На каком рисунке момент инерции стержня относительно оси O1O1
равен
13ml 2
?
12
80
6. На каком рисунке момент инерции стержня относительно оси O1O1
7ml 2
равен
?
3
2
O
O
O1
O1
O
3
O1
O
O1
O
1
O1
O1
4
O
O1
O1
O
5
O1
O
O1
O
6
O1
O
O1
O
7
O1
O
O1
Рис. 41
81
Задача 237
На рисунке 42 приведены пять одинаковых цилиндрических стержней из
одного и того же материала. Длина стержней l значительно больше радиуса
сечений r . Точка C - центр тяжести стержня, OO - ось вращения. Указать, у
какого стержня момент инерции относительно оси OO минимален, и у
какого стержня момент инерции относительно этой же оси максимален.
1
O
O
C
O
2
C
O
3
O
C
O
4
O
C
O
5
O
C
O
Рис. 42
Задача 238
На рисунках (Рис.43) изображены разные положения тонкого кольца массой
m и радиусом R относительно произвольной оси вращения O1O1 . Ось OO
проходит через центр кольца перпендикулярно его плоскости. Определить:
82
1. Какой рисунок соответствует кольцу с минимальным моментом
инерции относительно оси O1O1 ?
2. Какой рисунок соответствует кольцу с максимальным моментом
инерции относительно оси O1O1 ?
3. Какой рисунок соответствует кольцу с моментом инерции
относительно оси O1O1 равным I  2mR 2 ?
4. Какой рисунок соответствует кольцу с моментом инерции
относительно оси O1O1 равным I  5mR 2 ?
5. Какой рисунок соответствует кольцу с моментом инерции
6. Какой рисунок соответствует кольцу с моментом инерции
относительно оси O1O1 равным I  3,25mR2 ?
O
O
O1
2
1
R
O
O
O
3
4
O1
O1
O
O1
R
O
R
R/2
O1
O
5
O1
O
O
O1
R/2
O
Рис. 43
O1
83
Задача 239
На рисунке 44 приведены тела, имеющие одинаковые массы, но разную
форму. У какого из них минимальный момент инерции относительно оси
OO ? У какого из них максимальный момент инерции относительно оси OO ?
Геометрические параметры указаны на рисунках, где R - радиус шара.
O
1
2
O
3
O
O
O
O
R
5
O
O
4
O
O
Рис. 44
Задача 240
На рисунках (Рис. 45) представлены различные положения шара радиусом R
и массой m . Ось вращения OO проходит через центр шара, а ось O1O1
принимает различные положения, указанные на рисунках. Определить:
1. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 максимален?
2. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 минимален?
3. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 равен I  0,65mR2 ?
84
4. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 равен I  1,4mR2 ?
5. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 равен I  4,4mR2 ?
6. На каком рисунке изображен шар, момент инерции которого
относительно оси O1O1 равен I  2,65mR2 ?
2
1
O
O
O
O
R/2
O1
3
O1
4
O
O
R/2
O
O
O1
O1
R
O
O1
5
O1
R
O
O1
Рис. 45
O1
85
Задача 241
Два одинаковых стержня длиной 1,5 м и диаметром 10 см, выполненные из
стали плотностью 7800 кг/м3, соединены так, что образуют букву Т. Найти
моменты инерции системы относительно осей, совпадающих с осями
стержней.
Задача 242
Однородный тонкий диск имеет массу 800 г и радиус 10 см. Вычислите его
момент инерции относительно оси, перпендикулярной к плоскости диска и
проходящей через его центр.
Задача 243
Найти момент инерции равностороннего треугольника, сторонами которого
являются стержни длиной 20 см и массой 10 г, относительно оси,
проходящей через пересечение высот этого треугольника и перпендикулярно
его плоскости.
Задача 244
Проволочный равносторонний треугольник со стороной 10 см имеет массу 12
г. Определите момент инерции треугольника относительно оси, лежащей в
плоскости треугольника, и проходящей через его вершину параллельно
противоположной стороне.
Задача 245
В однородном диске радиусом 30 см и массой 1 кг вырезали круглое
отверстие радиусом 10 см, центр которого лежит на расстоянии 15 см от
центра диска. Вычислите момент инерции этого тела относительно оси,
перпендикулярной плоскости диска и проходящей через его центр.
Задача 246
В однородном диске радиусом 30 см и массой 1 кг вырезали круглое
отверстие диаметром 20 см, центр которого лежит на расстоянии 15 см от
центра диска. Вычислите момент инерции этого тела относительно оси,
перпендикулярной плоскости диска и проходящей через его центр.
Задача 247
Плоская однородная пластинка имеет длину одной из сторон 40 см и массу
900 г. Определите момент инерции пластинки относительно оси,
совпадающей с другой стороной.
Задача 248
Вывести формулу для расчета момента инерции однородной тонкой
прямоугольной пластинки массой m , длины a и ширины b относительно
86
перпендикулярной к плоскости пластинки оси, проходящей через ее центр
масс.
Задача 249
Вывести формулу для момента инерции кольца массой m , если его
внутренний радиус R1 , а внешний радиус R2 , относительно оси кольца,
перпендикулярной его плоскости.
Задача 250
Тонкий стержень имеет длину 30 см и массу 100 г. Чему равен момент
инерции стержня относительно оси, проходящей через его конец
перпендикулярно стержню.
Задача 251
Стороны проволочного прямоугольника равны 12 см и 16 см, а его масса
равномерно распределена по длине проволоки с линейной плотностью 0,1
кг/м. Вычислите момент инерции фигуры относительно оси, лежащей в ее
плоскости и проходящей через середины малых сторон.
Задача 252
Проволочный равносторонний треугольник имеет сторону длиной 30 см и
массу 300 г. Определите момент инерции треугольника относительно оси,
совпадающей с одной из сторон треугольника.
Задача 253
Вывести формулу для расчета момента инерции сплошного однородного
шара радиуса R и массы m относительно оси, проходящей через центр
шара.
Задача 254
Вывести формулу для расчета момента инерции полого однородного шара
(тонкой сферы) радиуса R и массы m относительно оси, проходящей через
центр шара.
Задача 255
Вывести формулу для расчета момента инерции прямого кругового
однородного конуса, радиус основания которого равен R , а масса m ,
относительно его оси.
Задача 256
Плоская прямоугольная однородная пластинка имеет длину одной из сторон
50 см и массу 600 г. Определите момент инерции пластинки относительно
оси, совпадающей с другой ее стороной.
87
Задача 257
Вывести формулу для расчета момента инерции однородной тонкой
прямоугольной пластинки массы m , длины a и ширины b относительно
перпендикулярной к пластинке оси, проходящей через одну из вершин
пластинки.
Задача 258
Два маленьких шарика массой 10 г каждый соединены тонким невесомым
стержнем длиной 20 см. Определите момент инерции системы относительно
оси, перпендикулярной к стержню и смещенной относительно его середины
по перпендикуляру на половину длины стержня.
Задача 259
Два маленьких шарика массой 10 г каждый соединены тонким невесомым
стержнем длиной 20 см. Определите момент инерции системы относительно
оси, перпендикулярной к стержню и проходящей через его центр масс.
Задача 260
Определить момент инерции цилиндрической муфты относительно оси,
совпадающей с осью симметрии. Масса муфты 2 кг, внутренний радиус 3 см,
внешний радиус 6 см. Вывести выражение для момента инерции такой
муфты.
Задача 261
Определить момент инерции полого шара массой 2 кг относительно оси,
совпадающей с касательной к шару. Внутренний радиус шара равен 3 см, а
внешний радиус равен 8 см.
Задача 262
В тонком диске вырезано симметрично четыре круглых отверстия радиусами
50 см на равных расстояниях 4 м от центра диска. Определить момент
инерции полученного тела относительно оси, проходящей через центр
тяжести диска перпендикулярно его плоскости. Масса диска 20 кг, радиус
диска 10 м.
Задача 263
Система состоит из двух взаимно-перпендикулярных стержней и шара (Рис.
46). Система тел может вращаться вокруг оси OO . Определить момент
инерции системы относительно этой оси, если масса большого стержня равна
2 кг, его длина равна l1  2 м. Масса малого стержня равна 1 кг, а его длина
равна l2  1 м. Масса шара равна 4 кг, а радиус R шара равен 0,5 м.
88
O
O
R
Рис. 46
Задача 264
Сплошной цилиндр массой m1  m и диаметром d1  4 x соединен стержнем
массой m2  m и длиной l  2 x с другим сплошным цилиндром массой
m3  2m и диаметром d 2  4 x , как показано на рисунке 47 Определить
момент инерции системы тел относительно указанных осей 1, 2, 3, 4, 5, 6, 7.
Оси 1, 3, 5, и 7 проходят вдоль боковой поверхности соответствующих
цилиндров. Оси 2 и 6 проходят через центры соответствующих цилиндров.
Ось 4 проходит через середину стержня, соединяющего цилиндры.
m
m
1
2
3
4
2m
5
Рис. 47
6
7
89
Задача 265
Полый цилиндр, внутренний диаметр которого равен 2x , внешний диаметр
равен 4x , а масса равна m , соединен стержнем массой m и длиной 2x со
сплошным цилиндром диаметром 4x и массой 2m (Рис. 48). Определить
момент инерции этой системы тел относительно осей 1, 2, 3, 4, 5, 6 и 7. Оси
1, 3, 5, и 7 проходят вдоль боковой поверхности соответствующих
цилиндров. Оси 2 и 6 проходят через центры соответствующих цилиндров.
Ось 4 проходит через середину стержня, соединяющего цилиндры.
1
2
3
4
5
6
7
Рис. 48
Задача 266
Сплошной шар диаметром 4x и массой m соединен тонким стержнем
длиной 2x и массой m со сплошным цилиндром диаметром 4x и массой 2m
(Рис. 49). Найти моменты инерции этой системы тел относительно осей 1, 2,
3, 4, 5, 6 и 7. Оси 1 и 3 проходят через касательную к шару, ось 2 проходит
через центр шара по его диаметру, оси 5 и 7 проходят вдоль боковой
поверхности цилиндра. Ось 6 проходят через центр цилиндра. Ось 4
проходит через середину стержня, соединяющего шар и цилиндр.
90
4x
4x
2x
m
1
m
2
3
2m
4
5
7
6
Рис. 49
Задача 267
Полый шар массой m и диаметром 4x соединен тонким стержнем массой m
и длиной 2x соединен со сплошным шаром диаметром 4x и массой 2m (Рис.
50). Определить моменты инерции системы тел относительно осей 1, 2, 3, 4,
5, 6 и 7. Оси 1, 3, 5, и 7 проходят по касательной к поверхности шаров. Оси 2
и 6 проходят через центры соответствующих шаров по их диаметрам. Ось 4
проходит через середину стержня, соединяющего шары.
4x
2x
m
1
4x
m
2
3
2m
4
5
6
7
Рис. 50
Задача 268
Два одинаковых сплошных конуса соединены своими основаниями. Общая
масса этих конусов равна m , а диаметр основания равен 4x (Рис. 51). Эта
система конусов соединена тонким стержнем массой m и длиной 2x со
сплошным цилиндром массой 2m и диаметром 4x . Найти моменты инерции
этой системы тел относительно осей 1, 2, 3, 4, 5, 6 и 7. . Оси 1 и 3 проходят по
91
краю основания конусов перпендикулярно диаметру общего основания, ось 2
проходит через ось симметрии конусов через центр их общего основания.
Оси 5 и 7 проходят по боковой поверхности цилиндра, ось 6 проходит через
ось цилиндра, а ось 4 проходит через середину стержня, соединяющего
систему из конусов и цилиндр.
4x
2x
m
m
1
4x
2
3
2m
4
5
6
7
Рис. 51
Задача 269
Два одинаковых сплошных конуса соединены своими основаниями. Общая
масса этих конусов равна m , а диаметр основания равен 4x (Рис. 52). Эта
система конусов соединена тонким стержнем массой m и длиной
2x со сплошным шаром массой 2m и диаметром 4x . Найти моменты
инерции этой системы тел относительно осей 1, 2, 3, 4, 5, 6 и 7. . Оси 1 и 3
проходят по краю основания конусов перпендикулярно диаметру общего
основания, ось 2 проходит через ось симметрии конусов через центр их
общего основания. Оси 5 и 7 проходят по касательной к шару, ось 6
проходит через центр шара по диаметру, а ось 4 проходит через середину
стержня, соединяющего систему из конусов и шар.
92
4x
2x
m
1
4x
m
2
3
4
2m
5
Рис. 52
6
7
93
8 Маятник Обербека
Задача 270
На рисунке 53 приведен график зависимости углового ускорения маятника
Обербека от момента силы натяжения нити. Используя график, определите
момент силы трения и момент инерции маятника для каждого маятника
30
20
10
1
3
2
Рис. 53
Задача 271
На рисунке 54 приведены графики зависимости углового ускорения от
момента силы натяжения нити для нескольких маятников Обербека.
Определить:
1. У какого маятника наибольший момент инерции;
2. У какого из маятников наименьший момент инерции;
3. У каких маятников одинаковые моменты инерции.
На всех графиках единицы измерения углового ускорения и момента сил
соответствуют системе СИ.
1
60
40
20
1
2
3
4
94
2
30
20
10
1
2
3
4
1
2
3
4
1
2
3
4
3
60
40
20
4
45
30
15
95
5
30
20
10
1
2
3
4
0,1
0,2
0,3
0,4
0,1
0,2
0,3
0,4
6
6
4
2
7
3
2
1
96
8
6
4
2
0,1
0,2
0,3
0,4
9
3
2
1
0,1
0,2
0,3
0,4
0,1
0,2
0,3
0,4
10
3
2
1
Рис. 54
97
Задача 272
На рисунке 55 отмечены величины углового ускорения, найденные из опыта
при нескольких значениях момента силы натяжения нити, для двух
маятников Обербека. Сравните моменты сил трения, действующих на
маятники.
1
20
2
10
0
0
2
4
6
8
M,
мНм
Рис. 55
Задача 273
Какие из соотношений, приведенных ниже, являются аналитическим
выражением основного закона динамики вращательного движения тела
вокруг неподвижной оси?
n
I 2
dL
dA
1. W 
; 2. I   mi ri 2 ; 3. M  I  ; 4. M 
; 5. M 
.
2
dt
d
i 1
Здесь M - момент силы; I - момент инерции тела относительно оси
вращения;  - угловая скорость вращения тела вокруг неподвижной оси;  угловое ускорение тела; W - кинетическая энергия; dA - элементарная
работа;  - угол поворота тела вокруг неподвижной оси; mi - элементарная
масса; ri - радиус окружности, по которой вращается точка с элементарной
массой вокруг неподвижной оси; t - время.
98
Задача 274
На рисунке 56 отмечены величины углового ускорения, найденные из опыта
при нескольких значениях момента силы натяжения нити, для двух
маятников Обербека. Определите моменты сил трения, действующих на
маятники.
1
30
20
2
10
0
1
2
3
4
5
М,мН
м
Рис. 56
Задача 275
На рисунке 57 отмечены величины углового ускорения, найденные из опыта
при нескольких значениях момента силы натяжения нити, для двух
маятников Обербека. Определите моменты сил трения, действующих на
маятники.
1
15
10
2
5
0
1
2
3
Рис. 57
4
5
М,мНм
99
Задача 276
На рисунке 58 отмечены величины углового ускорения, найденные из опыта
при нескольких значениях момента силы натяжения нити, для двух
маятников Обербека. Определите моменты инерции маятников
2
1
3
2
1
0
2
4
6
8
10
М,мНм
Рис. 58
Задача 277
В таблице 1 приведены значения момента сил натяжения нити и
соответствующие им величины углового ускорения и пяти маятников
Обербека. Определите, используя таблицу, какой из маятников имеет
наибольший момент силы трения, и какой из маятников имеет наименьший
момент силы трения
Таблица 1
М, 10-2 Нм
 ,c2
№1
№2
№3
№4
№5
2
4
6
8
10
5
5
2
2
1
15
10
8
4
5
25
15
14
6
9
35
20
20
8
13
45
25
26
10
17
Задача 278
В таблице 2 приведены значения момента сил натяжения нити и
соответствующие им величины углового ускорения и пяти маятников
Обербека. Определите, используя таблицу, какой из маятников имеет
наибольший момент инерции, и какой из маятников имеет наименьший
момент инерции
100
Таблица 2
М, 10-2 Нм
 ,c2
№1
№2
№3
№4
№5
0,2
0,4
0,6
0,8
1,0
0,5
0,5
0,2
0,2
0,1
1,5
1,0
0,8
0,4
0,5
2,5
1,5
1,4
0,6
0,9
3,5
2,0
2,0
0,8
1,3
4,5
2,5
2,6
1,0
1,7
Задача 279
В таблице 3 приведены значения момента сил натяжения нити и
соответствующие им величины углового ускорения и пяти маятников
Обербека. Определите, используя таблицу, какой из маятников имеет момент
сил трения, равный 1мНм .
Таблица 3
М, мНм
 ,c
2
№1
№2
№3
№4
№5
2
4
6
8
10
1
2
2
5
5
5
8
4
15
10
9
14
6
25
15
13
20
8
35
20
17
26
10
45
25
Задача 280
В таблице 4 приведены значения момента сил натяжения нити и
соответствующие им величины углового ускорения и пяти маятников
Обербека. Определите, используя таблицу, какой из маятников имеет момент
инерции, равный 1кгм2 , и какой из маятников имеет момент инерции 0,5кгм2
Таблица 4
М, Нм
 ,c
2
№1
№2
№3
№4
0,2
0,4
0,6
0,8
1,0
0,1
0,2
0,2
0,5
0,5
0,8
0,4
1,5
0,9
1,4
0,6
2,5
1,3
2,0
0,8
3,5
1,7
2,6
1,0
4,5
101
№5
0,5
1,0
1,5
2,0
2,5
Задача 281
На какое расстояние необходимо переместить грузы на маятнике Обербека,
чтобы момент инерции маятника уменьшился в 4 раза?
Задача 282
Какая из приведенных ниже формул является выражением теоремы Гюйгенса
– Штейнера?
n
dL
1
1. I  mr ; 2. I   mi ri 2 ; 3. I  I 0  md 2 ; 4. I  mR 2 ; 5. M 
.
dt
2
i 1
Здесь I - момент инерции тела относительно неподвижной оси;
m - масса материальной точки; r - радиус, по которому вращается точка;
mi - масса малого (точечного) элемента вращающегося тела; ri - радиус, по
которому вращается малый элемент тела; I 0 - момент инерции тела
относительно оси, проходящей через центр масс; d - расстояние между осью,
проходящей через центр масс, и некоторой другой осью, параллельной оси,
проходящей через центр масс; R - радиус некоторого тела; M - момент
силы; L - момент импульса тела; t - время.
2
Задача 283
Какие из приведенных ниже формул используются при выводе рабочей
формулы для экспериментального определения момента инерции маятника
Обербека?
I 2
dL
; 2. M 
 I  ; 3. A  M  ; 4. L  I  ; 5. I  I 0  md 2 .
2
dt
Здесь I - момент инерции тела относительно неподвижной оси;
m - масса материальной точки;  - угловая скорость вращения тела;
W - кинетическая энергия тела; I 0 - момент инерции тела относительно оси,
проходящей через центр масс; d - расстояние между осью, проходящей через
центр масс, и некоторой другой осью, параллельной оси, проходящей через
центр масс;  - угловое ускорение; M - момент силы; L - момент импульса
тела; t - время; A - работа;  - угол поворота.
1. W 
Задача 284
Какие из формул, приведенных ниже, используются для определения
момента сил трения маятника Обербека?
1. A  M  ; 2. M  I  ; 3.  
S
; 4. A  mgh ; 5. S  h1  h2 ; 6. h  h1  h2
r
102
Здесь I - момент инерции тела относительно неподвижной оси; m - масса
груза;  - угловое ускорение; M - момент силы; A - работа;  - угол
поворота; h1 - высота, с которой опускается груз на маятнике Обербека, h2 высота, на которую поднимается груз на маятнике Обербека.
Задача 285
Какая из формул, приведенных ниже, является рабочей формулой для
определения момента инерции маятника Обербека из опыта?
m  g  a  r  M mp
1
2mgh
M
1. I  ml 2 ; 2. I 
; 3. I 
; 4. I  I 0  4mR 2 ; 5. I 
.
6



Здесь I - момент инерции тела относительно неподвижной оси; m - масса
груза;  - угловое ускорение; M - момент силы; l - длина стержня;
 - угол поворота; g - ускорение свободного падения; a - ускорение груза;
M mp - момент сил трения; r - радиус шкива.
Задача 286
Определите момент инерции маятника Обербека, если груз массой 0,1 кг
опускается с ускорением 0,05 м/с2, а груз массой 0,2 кг опускается с
ускорением 0,125 м/с2. Считать, что момент сил трения одинаков для обоих
случаев. Радиус шкива маятника равен 0,02 м.
Задача 287
Определите момент сил трения, действующих на маятник Обербека, если
груз массой 0,2 кг спускается с ускорением 0,1 м/с2. Радиус шкива маятника
равен 0,03 м, момент инерции маятника I  7,66 103 кгм2.
Задача 288
Определите момент сил трения, действующих на маятник Обербека, если
груз массой 0,4 кг, подвешенный на нити, закрепленной на шкиве маятника,
падая с высоты h1  1,6 м, снова поднимается на высоту h2  0,85 м. Диаметр
шкива маятника равен 0,10 м.
Задача 289
Определите момент сил трения, действующих на маятник Обербека, если
груз массой 0,2 кг, подвешенный на нити, закрепленной на шкиве маятника,
падая с высоты h1  1,6 м, снова поднимается на высоту h2  0,85 м. Диаметр
шкива маятника равен 0,10 м.
103
Задача 290
С какой высоты h1 падает груз массой 0,4 кг, подвешенный на нити,
закрепленной на шкиве маятника Обербека, если после падения он снова
поднимается на высоту h2  1,2 м? Момент силы трения, действующей на
маятник, равен 4,9 102 Нм, диаметр шкива маятника равен 0,1 м.
Задача 291
На какую высоту h2 поднимется груз массой 0,3 кг, закрепленный на нити
маятника Обербека, если момент силы трения, действующей на маятник,
равен 2,45 102 Нм, диаметр шкива маятника равен 0,1 м? Первоначальная
высота груза равна h1  1, 4 м.
Задача 292
На рисунке (Рис. 59) изображен маятник Обербека с четырьмя одинаковыми
грузами. Ось вращения проходит через точку O перпендикулярно плоскости
рисунка. По какой из приведенных ниже формул, можно определить момент
инерции системы? Массой стержней можно пренебречь. Грузы массой m
можно принимать за материальные точки.
m
R/2
m
m
O
R
m
Рис. 59
1. I  4mR 2 ; 2. I  2,5mR2 ; 3. I  0,5mR2 ; 4. I  2mR 2 ; 5. I  mR 2 .
Задача 293
Радиус вала махового колеса равен 5 см. На вал намотан шнур, к концу
которого привязан груз массой 200 г. Под действием силы тяжести груз
опускается за 5 с с высоты 1,5 м, а затем вследствие вращения колеса по
инерции поднимается на высоту 0,8 м. Определить момент инерции вала
махового колеса и момент сил трения, действующих на колесо.
104
9. Определение момента инерции тел с помощью крутильных колебаний
Задача 294
Какая из формул, приведенных ниже, является рабочей формулой для
определения момента инерции круглой платформы трифилярного подвеса из
опыта?
2mgh
mRrg
M
1
1. I  mR 2 ; 2. I 
; 3. I  I 0  md 2 ; 4. I  kT 2 , где k 
; 5. I 
.
2
2

4 l

2
Здесь I - момент инерции платформы; m - масса платформы; R - радиус
платформы; r - радиус верхнего диска трифилярного подвеса; g - ускорение
свободного падения; h - высота, на которую поднимается платформа;
 - угловая скорость вращения платформы;  - угловое ускорение
платформы; l - длина нитей трифилярного подвеса; T - период колебаний
платформы; I 0 - момент инерции платформы относительно оси, проходящей
через центр масс; d - расстояние между осями вращения; M - момент сил,
действующих на платформу.
Задача 295
Какие формулы, из приведенных ниже формул, не используются при выводе
рабочей формулы для определения момента инерции круглой платформы
трифилярного подвеса из опыта?
I 2
I 2
d
 mgh ; 4.    0 sin t ; 5.  
1. W 
; 2. M  I  ; 3.
.
2
2
dt
Здесь I - момент инерции платформы; m - масса платформы; g - ускорение
свободного падения; h - высота, на которую поднимается платформа;  угловая скорость вращения платформы;  - угловое ускорение платформы;
M - момент сил, действующих на платформу; W - кинетическая энергия
платформы;  - угол поворота платформы в момент времени t ;  0 амплитудное значение угла поворота платформы.
Задача 296
Какая из формул, приведенных ниже, используется для вывода рабочей
формулы для определения момента инерции круглой платформы
трифилярного подвеса из опыта?
I 2
I 2
 mgh ; 5. A 
1. I  I 0  md ; 2. A  M  ; 3. M  I  ; 4.
.
2
2
2
105
Здесь I - момент инерции платформы; m - масса платформы; g - ускорение
свободного падения; h - высота, на которую поднимается платформа;  угловая скорость вращения платформы;  - угловое ускорение платформы;
I 0 - момент инерции платформы относительно оси, проходящей через центр
масс; d - расстояние между осями вращения; M - момент сил, действующих
на платформу; A - работа сил, действующих на платформу.
Задача 297
На рисунке 60 представлена платформа радиусом 10 см и массой 1600 г. На
каком расстоянии d от оси вращения, проходящей через ось платформы,
необходимо расположить два одинаковых сплошных цилиндра массой 1 кг
каждый и радиусом 2 см, чтобы момент инерции всей системы стал равным
13,4 103 кгм2?
O
d
O
Рис. 60
Задача 298
На рисунке 61 изображен трифилярный подвес. Масса нижнего диска 0,8 кг,
его радиус 10 см. Радиус верхнего диска равен 4 см. Длина нитей равна 1 м.
Чему равен период колебаний нижнего диска, если его привести в
крутильное колебание?
106
r
R
O
Рис. 61
Задача 299
Определить массу цилиндра, помещенного в центр нижней платформы (Рис.
61), если период колебаний системы стал равным 1,57 с. Необходимые
данные взять из предыдущего задания.
Задача 300
В центре платформы с трифилярным подвесом расположены два одинаковых
цилиндра массой m и радиусом r каждый. Цилиндры поставлены друг на
друга. Как изменится момент инерции цилиндров относительно оси
платформы, если их перенести на расстояние a от центра платформы,
расположив симметрично?
Задача 301
На платформу с трифилярным подвесом положили груз, вследствие чего
отношение момента инерции платформы с грузом к их массе увеличилось в 4
раза. Во сколько раз изменился период колебаний платформы?
Задача 302
На платформу с трифилярным подвесом положили груз, вследствие чего
период колебаний платформы увеличился в
2 раз. Во сколько раз
изменилось отношение момента инерции платформы с грузом к их массе.
107
Задача 303
Диск радиусом 0,2 м и массой 1 кг подвешен на трех нитях, закрепленных в
одной точке (Рис. 62). Длина нитей равна 2 м. Определить силу натяжения
каждой нити.
O
O
Рис. 62
Задача 304
Платформа на трифилярном подвесе (Рис. 63) имеет массу 0,5 кг и радиус 10
см. Радиус верхнего диска равен 5 см. длина нитей равна 1,5 м. Определить
силу натяжения нитей.
r
O
R
O
Рис. 63
108
Задача 305
Диск радиусом 0,2 м и массой 0,45 кг подвешен на трех нитях, закрепленных
в одной точке (Рис. 62). Длина нити 0,5 м. Определить силу натяжения нитей.
Задача 306
Платформа на трифилярном подвесе в момент прохождения положения
равновесия имеет угловую скорость 0,54 рад/с. Определить, на какую высоту
поднимется платформа в момент наибольшего отклонения от положения
равновесия. Радиус платформы равен 0,1 м.
Задача 307
Платформа на трифилярном подвесе совершает колебания, согласно закону
  0,087cos2 t (рад). Определить наибольшую угловую скорость и
наибольшую кинетическую энергию платформы, если ее масса равна 0,5 кг, а
радиус равен 0,1 м.
Задача 308
Платформа на трифилярном подвесе совершает колебания, согласно закону
  0,174cos t (рад). Определить высоту, на которую приподнимается
платформа в момент наибольшего отклонения от положения равновесия.
Радиус платформы равен 10 см. Определить период колебаний платформы.
10. Баллистический и крутильно-баллистический маятники
Задача 309
Частица движется с постоянной скоростью вдоль прямой линии. Как
изменяется с течением времени момент импульса частицы, вычисленный
относительно любой точки, не лежащей на этой прямой?
Задача 310
Используя закон сохранения момента импульса. Объясните, почему вертолет
должен иметь больше одного пропеллера. Укажите один или несколько
способов размещения второго пропеллера, функция которого состоит в
сообщении вертолету устойчивости.
Задача 311
Колесо свободно вращается относительно вертикальной оси с постоянной
угловой скоростью. Колесо понемногу крошится, и от него отлетают
обломки. Как это повлияет на скорость колеса? Сохраняется ли его момент
импульса? Сохраняется ли кинетическая энергия колеса?
109
Задача 312
Стержень может вращаться вокруг оси, проходящей через его конец,
который закреплен в точке O (Рис. 64). В нижний конец стержня попадает
пуля, летящая горизонтально со скоростью V . Укажите направление
момента импульса стержня.
O
Рис. 64
Задача 313
Стержень длиной 2 м может вращаться вокруг оси O (Рис. 64). Масса
стержня равна 3 кг. На какой угол отклонится стержень, если в ее конец
попадает пуля массой 10 г, летящая со скоростью 500 м/с, и застревает в нем?
Задача 314
Стержень длиной 1,5 м может вращаться вокруг оси O (Рис. 64). Масса
стержня равна 3 кг. На какой угол отклонится стержень, если в ее конец
попадает пуля массой 10 г, летящая со скоростью 600 м/с, и застревает в нем?
Задача 315
Деревянный стержень массой 1 кг и длиной 2 м может вращаться вокруг оси,
проходящей через его середину (Рис. 65). В конец стержня попадает
пластмассовый шарик массой 10 г, летящий со скоростью 50 м/с. Определите
угловую скорость, с которой начинает вращаться стержень. Удар шарика о
стержень считать абсолютно упругим.
O
Рис. 65
110
Задача 316
Пулч массой 10 г попадает в стержень, который может вращаться вокруг оси,
проходящей через точку O (Рис. 66) и застревает в нем. При этом стержень
отклоняется от вертикали на угол 300. Масса стержня равна 2 кг, длина
стержня равна 1 м. Определить скорость пули.
O
C
Рис. 66
Задача 317
Стержень длиной 1,5 м может вращаться вокруг оси, проходящей через его
середину (Рис. 67). Найдите момент инерции стержня после попадания в его
конец пули, импульс которой до удара о стержень равен 6 кгм/с. Пуля
застревает в стержне, который после попадания в него пули отклоняется от
вертикали на угол 300.
O
Рис. 67
Задача 318
Маятник длиной 2 м и массой 3 кг может вращаться вокруг горизонтальной
оси, проходящей через его конец в точке O (Рис. 68). На расстоянии 1 м от
оси вращения укреплен пластилиновый шарик B массой 200 г. Пуля массой
10 г, летящая горизонтально со скоростью 1000 м/с, попадает в
пластилиновый шарик и застревает в нем. Вычислите линейную скорость
пластилинового шарика после попадания в него пули.
111
O
B
Рис. 68
Задача 319
Горизонтально расположенный деревянный стержень массой 1 кг и длиной 2
м может вращаться вокруг вертикальной оси, проходящей через его середину
(точка O ). В конец стержня попадает и застревает в нем горизонтально
летящая пуля массой 5 г (Рис. 69). Пуля летит перпендикулярно стержню со
скоростью 200 м/с. Определить угловую скорость, с которой начнет
вращаться стержень.
O
Рис. 69
Задача 320
Пуля массой 1 г, летящая горизонтально со скоростью 300 м/с, попадает в
шар массой 1 кг, лежащий на горизонтальной поверхности, и пробивает его.
Какую скорость приобретает шар, если пуля вылетела из шара со скоростью
в два раза меньшей, чем до удара о шар. Трением шара о поверхность
пренебречь. Считать, что траектория полета пули проходит через центр шара.
Задача 321
Пуля массой 5 г попадает в деревянный брусок массой 0,5 кг, подвешенный
на нити длиной 1 м, и застревает в нем (баллистический маятник). На какой
угол отклонится нить маятника от вертикали, если скорость пули до удара
была 400 м/с?
112
Задача 322
На горизонтальном деревянном столе лежит деревянный брусок массой 5 кг.
В брусок попадает пуля массой 9 г. После попадания пули в брусок он
переместился по столу на расстояние 25 см и остановился. Определить
скорость пули до удара о брусок, если коэффициент трения бруска о
поверхность стола равен 0,2.
Задача 323
Пуля массой 5 г, летящая горизонтально со скоростью 400 м/с, попадает по
линии центра в однородный шар массой 1 кг и радиусом 10 см, лежащий на
горизонтальной поверхности. Пуля проходит по диаметру весь шар и
застревает у его поверхности. Определите среднюю силу сопротивления
движению шара, если шар остался неподвижным.
Задача 324
Из ружья стреляют в спичечный коробок, лежащий на расстоянии 30 см от
края стола. Пуля массой 1 г, летящая горизонтально со скоростью 150м/с,
пробивает коробок и вылетает из него с в два раза меньшей скоростью.
Масса коробка равна 50 г. При каком коэффициенте трения между коробком
и столом коробок упадет со стола?
Задача 325
В стержень длиной 1,5 м и массой 2 кг, имеющий горизонтальную ось
вращения, проходящую через его конец (точка O ), попадает пуля массой 10
г, летящая со скоростью 400 м/с (Рис. 70). Линия движения пули проходит на
расстоянии l1  1 м от оси вращения. Определите кинетическую энергию
стержня после попадания в него пули. Удар пули о стержень считать
абсолютно неупругим.
O
Рис. 70
Задача 326
Пуля массой 10 г, имеющая начальную скорость, пробивает подвешенный на
нити свинцовый шар массой 0,2 кг и вылетает из него с половинной
113
скоростью. Какая часть кинетической энергии пули перешла в тепловую
энергию?
Задача 327
Предполагая, что сила, действующая на пулю в стволе ружья. Изменяется со
временем в соответствии с уравнением F  480  1,6 105 t ( t измеряется в
секундах, F измеряется в ньютонах). Определите:
1) Импульс, который получила пуля за время действия силы;
2) Скорость вылета пули из ствола, если масса пули равна 5 г.
Задача 328
Пуля в стволе автомата движется с ускорением, зависимость которого от
времени представлена на графике (Рис. 71). Масса пули 8 г. Определите:
1) Скорость пули, которую она приобрела к моменту вылета из ствола;
2) Суммарный импульс, который получила пуля за время движения в
стволе.
a, м/с2
8
6
4
2
0
2
1
t, 10-2 с
Рис. 71
Задача 329
На пулю в стволе автомата Калашникова действует сила давления пороховых
газов, зависимость которой от времени представлена на рисунке (Рис. 72).
Пользуясь графиком, определите:
1) Суммарный импульс, который получила пуля за время движения в
стволе;
2) Скорость пули, приобретенную к моменту вылета из ствола автомата,
если масса пули равна 8 г.
114
F, H
600
300
t, 10-2 с
0
2
1
Рис. 72
Задача 330
В стволе духового ружья на пулю действует сила, зависимость которой от
координаты x представлена на графике (Рис. 73). Ось OX направлена вдоль
ствола, начало координат совпадает с начальным положением пули.
Пользуясь графиком, определите:
1) Работу, совершенную сжатым воздухом за время движения пули в
стволе;
2) Скорость пули при вылете из ружья. Масса пули равна 7 г. потерями
энергии пренебречь.
F, H
400
300
200
100
x, м
0
0,1
0,2
0,3
0,4
0,5
Рис. 73
Задача 331
На пулю в стволе ружья действует сила, зависимость которой от времени
представлена на графике (Рис. 74). Пользуясь графиком, определите:
1) Импульс, который получила пуля за время движения в стволе;
115
2) Массу пули, если в результате действия силы она приобретает скорость
400 м/с.
F, H
800
400
0
5
t, 10-3 с
10
Рис. 74
Задача 332
Какие из приведенных ниже соотношений определяют потенциальную
энергию однородного стержня баллистического маятника, имеющего массу
m и длину l , при отклонении на угол  ? На рисунке (Рис. 75) показано
положение стержня, соответствующее этому моменту времени.
h
M
S
Рис. 75
1.
1 2 2
h

s2
ml  ; 2. mgh ; 3. mg ; 4. mg ; 5. mg sin 2 .
6
2
2
4l
Задача 333
Определить максимальную потенциальную энергию однородного стержня
баллистического маятника, если после попадания в мишень, укрепленную на
его конце пули, угол отклонения стержня от вертикали оказался равным 600.
Масса стержня равна 2 кг, а его длина равна 1,5 м.
116
Задача 334
Определите максимальную высоту, на которую поднимется центр масс
однородного стержня баллистического маятника при попадании в его
мишень пули массой 4 г, движущейся со скоростью 300 м/с. Масса стержня
равна 3 кг, масса мишени равна 495 г. Трением в подвесе маятника и
сопротивлением воздуха пренебречь. Удар пули о мишень считать
неупругим.
Задача 335
Для определения опытным путем скорости полета пули используются два
баллистических маятника. Один из маятников представляет собой
однородный стержень длиной l и массой m с мишенью массой M на конце.
Другой конец маятника закреплен на неподвижной оси. Его можно
рассматривать как физический маятник. Второй баллистический маятник
можно рассматривать как математический маятник с длиной нити, равной
длине стержня, с мишенью такой же массы на конце. Линейными размерами
мишени по сравнению с длиной нити или стержня можно пренебречь. Во
сколько раз изменится линейное отклонение мишени от положения
равновесия при попадании в нее пули при замене физического маятника
математическим маятником? Считать, что масса пули и скорость движения
пули одинаковы в этих опытах. Масса пули значительно меньше массы
стержня и массы мишени. Потерями энергии при трении в подвесах и
сопротивлении воздуха пренебречь. Вычисления провести для случая, когда
масса стержня равна 3 кг, а масса мишени равна 1 кг.
Задача 336
В таблице приведены значения масс стержней m и масс мишеней M для
пяти баллистических маятников, имеющих одинаковую длину стержня.
Определить:
1) У какого из этих маятников будет наибольший угол отклонения от
вертикали после попадания пули в мишень;
2) У какого из этих маятников будет наименьший угол отклонения от
вертикали после попадания пули в мишень;
3) У какого из этих маятников центр тяжести мишени после попадания
пули поднимется на наибольшую высоту;
4) У какого из этих маятников центр тяжести мишени после попадания
пули поднимется на наименьшую высоту.
Считать массу пули намного меньше массы стержня и массы мишени. Масса
пули и ее скорость во всех опытах одинаковая. В исходном состоянии
маятники покоятся.
117
Таблица 5
№
Массы
m, кг
M, кг
1
2
3
4
5
1
2
3
4
6
1,5
0,5
1
2
0,5
Задача 337
При попадании пули в мишень баллистического маятника в виде
однородного стержня массой m и длиной l центр масс мишени поднялся на
высоту h1 . Масса мишени равна половине массы стержня M  0,5m . Во
сколько раз изменится высота, на которую поднимется центр масс мишени,
если массу мишени увеличить вдвое? Масса пули и ее скорость не
изменяются. Масса пули много меньше массы стержня и массы мишеней.
Задача 338
Скорость пули определяют с помощью двух баллистических маятников.
Один маятник представляет собой стержень длиной l и массой 3 кг, на конце
которого закреплена мишень массой 1 кг (физический маятник). Другой
маятник представляет собой мишень, подвешенную на длинной невесомой
нити (математический маятник). Масса мишени второго маятника также
равна 1 кг. После попадания пули в мишени маятников оба маятника
отклонились от положения равновесия на один и тот же угол. Во сколько раз
отличается длина нити математического маятника от длины стержня
физического маятника? Считать, что масса пули и ее скорость в обоих
опытах одинакова. Масса пули много меньше массы мишеней и массы
стержня.
Задача 339
При попадании пули в мишень баллистического маятника в виде стержня
массой m и длиной l центр тяжести мишени поднимается на высоту h1 . Как
изменится высота, на которую поднимется центр тяжести мишени, если
массу стержня и массу мишени увеличить в два раза? Масса пули, ее
скорость и длина стержня не изменяются. Масса пули много меньше массы
стержня и массы мишени. Укажите правильный ответ из приведенных ниже
ответов:
1. Увеличится в два раза; 2. Уменьшится в два раза; 3. Увеличится в
четыре раза; 4. Уменьшится в четыре раза; 5. Не изменится.
118
Задача 340
При определении скорости полета пули с помощью баллистического
маятника в виде однородного стержня длиной l и массой 3 кг и массой
мишени M 1  1 кг, закрепленной на конце стержня (физический маятник).
Мишень после попадания в нее пули поднялась на высоту h1 относительно
положения равновесия. При попадании пули в мишень массой M 2 ,
подвешенной на тонкой нерастяжимой нити (математический маятник),
высота подъема мишени оказалась такой же: h1  h2 . Во сколько раз
отличается масса мишени физического маятника от массы мишени
математического маятника? Трением в подвесе и сопротивлением воздуха
пренебречь. Масса и скорость пули не изменялись. Масса пули много
меньше массы стержня и массы мишеней.
Задача 341
Для определения опытным путем скорости полета пули используются два
баллистических маятника. Один из маятников представляет собой
однородный стержень длиной l и массой m с мишенью массой M на конце.
Другой конец маятника закреплен на неподвижной оси. Его можно
рассматривать как физический маятник. Второй баллистический маятник
можно рассматривать как математический маятник с длиной нити, равной
длине стержня, с мишенью такой же массы на конце. Линейными размерами
мишени по сравнению с длиной нити или стержня можно пренебречь. Во
сколько раз изменится высота, на которую поднимется мишень при
попадании в нее пули при замене физического маятника математическим
маятником? Считать, что масса пули и скорость движения пули одинаковы в
этих опытах. Масса пули значительно меньше массы стержня и массы
мишени. Потерями энергии при трении в подвесах и сопротивлении воздуха
пренебречь. Вычисления провести для случая, когда масса стержня равна 6
кг, а масса мишени равна 2 кг.
Задача 342
Модуль кручения спиральной пружины равен 2 Нм/рад. Пружину закрутили
на 10 оборотов. Какая работа была совершена при этом?
Задача 343
При попадании пули в диск крутильно-баллистического маятника он
совершил 10 полных колебаний за 5 с. Определите момент инерции
маятника, если модуль кручения нити – подвеса равен 12 Нм/рад.
Задача 344
Стержень длиной 1 м и массой 1 кг может вращаться вокруг оси, проходящей
через его середину (точка O ) перпендикулярно стержню. На концах стержня
укреплены шары массами 0,5 кг (Рис. 76). В один из шаров попадает пуля
массой 5 г, летящая горизонтально со скоростью 500 м/с. Пуля застревает в
119
стержне. Определить угловую скорость, с которой начнет вращаться
стержень после попадания в него пули.
O
Рис. 76
Задача 345
На рисунке (Рис. 77) представлена схема крутильно–баллистического
маятника. Грузы массой m закреплены на расстояниях R  0,4 м от
проволоки OA , на которой подвешен стержень. Длина проволоки OA равна
l  1 м, диаметр проволоки равен d  2 мм. Пуля массой 5 г попадает в центр
груза в точку C . При этом маятник поворачивается на угол   0,2 рад.
Определить скорость пули, если момент инерции маятника равен I  0,02
кгм2.
R
O
C
m
m
A
Рис. 77
Задача 346
Пуля массой 5 г, двигаясь со скоростью 1000 м/с, попадает в точку B диска
крутильно-баллистического маятника (Рис. 78). Точка B расположена на
расстоянии r  0,5 м от оси вращения. Момент инерции маятника равен
120
I  0,05 кгм2. Определить начальную угловую скорость поворота маятника и
линейную скорость движения центра диска точки B .
r
B
Рис. 78
Задача 347
Пуля массой m  7 г попадает в крутильно – баллистический маятник и
застревает в нем. Маятник после этого совершает колебания, описываемые
уравнением   0,087sin0,8 t рад. Определить период колебаний маятника и
скорость пули, если момент инерции маятника равен I  2 кгм2, а расстояние
от оси вращения маятника до траектории полета пули (по нормали) равно
r  0,3 м.
Задача 348
Пуля массой 5 г попадает в крутильно – баллистический маятник и
застревает в нем. Маятник после этого совершает колебания, график которых
представлен на рисунке (Рис. 79). Момент инерции маятника равен 0,5 кгм2, а
расстояние от оси вращения маятника до траектории полета пули (по
нормали) равно 0,2 м. Определить скорость полета пули.
Задача 349
Крутильный маятник подвешен на проволоке, модуль кручения которой
равен 0,5 Нм/рад. После попадания в маятник пули он начинает колебаться,
согласно уравнению   0,122sin0,8 t рад. Определить момент инерции
маятника.
Задача 350
Крутильный маятник, момент инерции которого равен 0,03 кгм2, подвешен
на проволоке. В маятник попадает пуля, после чего он начинает колебаться
согласно уравнению   0,21sin  t рад. Определить модуль кручения
проволоки подвеса маятника.
121
10
5
0
1
2
3
4
t, c
-10
-5
Рис.79
Задача 351
Крутильно – баллистический маятник подвесили на стальной проволоке,
модуль кручения которой равен 0,8 Нм/рад. В маятник попадает пуля,
летящая горизонтально со скоростью 50 м/с. После попадания пули маятник
приходит в колебательное движение, график которого представлен на
рисунке (Рис. 80). Определить момент инерции маятника, его полную
механическую энергию и долю механической энергии, перешедшей во
внутреннюю энергию при неупругом взаимодействии маятника и пули.
Масса пули равна 5 г.
20
10
0
0
1
2
3
-20
-10
Рис. 80
4
t, c
122
Задача 352
Крутильно – баллистический маятник, момент инерции которого равен 0,08
кгм2, приводится в колебательное движение. На рисунке (Рис. 81)
представлен график зависимости потенциальной энергии маятника от
времени. Определить, используя график, модуль кручения подвеса маятника
и максимальный угол поворота маятника.
Еп, 10-3 Дж
6
4
2
2
1
0
3
t, c
4
Рис. 81
Задача 353
Крутильно – баллистический маятник после попадания в него пули
совершает колебательное движение. На рисунке (Рис. 82) представлен
график зависимости потенциальной энергии маятника от угла поворота  .
Используя график, определите: 1) модуль кручения подвеса маятника; 2)
момент инерции маятника. Период колебаний маятника равен 1,5 с.
Еп, 10-3 Дж
4
3
2
1
-6
-4
-2
0
Рис. 82
2
4
6
123
Задача 354
Крутильно – баллистический маятник представляет собой систему,
состоящую из двух одинаковых грузов на стержне, закрепленном посередине
стальной проволоки на одинаковых расстояниях R  0,4 мот нее (Рис. 83).
Верхний и нижний концы проволоки жестко закреплены. Длина проволоки
l  2 м, диаметр проволоки d  2 мм. Пуля массой 10 г попадает в центр
одного из грузов, и маятник, обладающий моментом инерции 1 кгм 2,
поворачивается на угол   100 рад. Определить скорость пули. Крутящий
 Gd 4
момент проволоки определяется формулой M 
, где G - модуль
32l
сдвига материала проволоки. Для стали модуль сдвига равен G  8 1010 Н/м2.
Рис. 83
124
Литература
1.
2.
3.
4.
5.
Савельев
Сивухин
Яворский, Детлаф
Алешкевич