РГР2_524

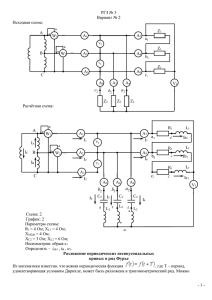
Государственное образовательное учреждение высшего профессионального
образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Теория общей электротехники
Расчетно-графическая работа №2
«Расчет линейной цепи синусоидального тока»
Вариант №524
Выполнил
Студент группы 8в82
___________________________
Сафронов Б.А.
(подпись/дата)
Проверил преподаватель:__________________________
(подпись/дата)
Томск 2010
Васильева О.В.
Условия задачи:
E
R
C
φ
L1
L2
f
В
Ом
МкФ
град
Гн
Гн
Гц
15
25
220
90
0,12
0,12
50
Схема:
Задание:
1.
В исходной цепи с ЭДС e(t )  2 E sin(t   ) рассчитать токи ветвей и составить
баланс мощностей (активных и реактивных). Коэффициент связи k  0,9 . Взаимная
индуктивность M  k L1 L2 .
Произвести развязку индуктивной связи и найти:

токи во всех ветвях методом узловых потенциалов;

токи во всех ветвях методом контурных токов;

ток в ветви с индуктивностью L2 метом эквивалентного генератора.
2.
Построить в одних осях векторные диаграммы токов (лучевую) и напряжений
(топографическую).
3.
Определить показание электродинамического вольтметра аналитически и по
топографической диаграмме.
4.
Подтвердить расчеты пунктов 1, 3 ,проделав работу на ElectronicsWorkbench
1. Рассчитаем токи ветвей без развязки индуктивной связи.
Составим уравнения для мгновенных значений токов и напряжений:
i i i  0
1
2
3
di
i R  L1
1
1
dt
di
 M
2
dt
di
 i R  L2
2
2
dt
di
 M
1
dt
 e( t )
di
di

1
2
1
i R   i d t  i R  L2
 M
 0
3
3
2

c
dt
dt

Запишем в комплексной форме:
I I I  0
1
2
3
I R  1i Xl1 I  i Xm I  I R  i Xl2 I  i Xm I  E
1
1
2
2
2
1
I R  i Xc I  I R  i Xl2 I  i Xm I  0
3
3
2
2
1
Рассчитаем сопротивления катушек и конденсатора:
1
Xl1   L1
Xl1  37.699
Xc 
Xl2   L2
Xl2  37.699
Xc  14.469 Ом
 C
В исходной цепи с ЭДС e(t )  2 E sin(t   ) рассчитываем токи ветвей:
1
1
1 



A  R  i Xl1  i Xm i Xm  R  i Xl2
0


i Xm
R  i Xl2
R  i Xc 

 0.087  0.369i



I  A  B   1.241  10 3  0.218i 


 0.086  0.151i
 А
0.379 

 

I  0.218 


 0.174  А
1
0
B   E 
 
0
Проверяем правильность вычислений через баланс активной(Р) и реактивной(Q) мощностей:

S  I  E
1
S  5.533  1.308i
 1 2  R I2 2  R I3 2
P  R I
P  5.533
 1 2  Xl2 I2 2  Xc I3 2  2 I1  I2 Xmcos argI1  argI2
Q  Xl1 I
Q  1.308
Запишем уравнения для мгновенных значений токов:

 1

 2

 3
i1( t)  I  sin  t  arg I
1
i2( t)  I  sin  t  arg I
2
i3( t)  I  sin  t  arg I
3
Построим график зависимости i от t:
T 
2 

t  00.01 T  2 T
1
0.5
i1( t )
i2( t )
0
i3( t )
0.01
0.02
 0.5
1
t
0.03
0.04
Запишем уравнения для мгновенных значений напряжений:
u2( t) 

 1 
2 I  z1  sin  t  arg I  z1
2
2
u3( t) 
2 I  z3  sin  t  arg I  z3
u1( t) 
2 I  z1 sin  t  arg I  z1
1
3

 3 
построим график зависимости U от t
z1  i ( Xl1  Xm)  R
z2  R  i ( Xl2  Xm)
z3  R  i ( Xm  Xc)
15
u1( t )
7.5
u2( t )
0
0.01
0.02
u3( t )
 7.5
 15
t
0.03
0.04
2. Производим развязку цепи
Т.к. включение согласное, мы добавляем
катушку с индуктивностью М и уменьшаем
индуктивность катушек L1 и L2 на М.
Теперь упрощаем схему, заменяя сопротивления:
z1  i ( Xl1  Xm)  R Ом
z2  R  i ( Xl2  Xm) Ом
z3  R  i ( Xm  Xc) Ом
Найдем проводимость ветвей.
y1 
1
Z1
y2 
1
y3 
Z2
1
Z3
Рисуем схему замещения.
F1 
( E y1)
y1  y2  y3
I1 
I2 
I3 
( E  F1)
Z1
F1
Z2
 0.087  0.369i
3
 1.241  10
F1
Z3
 0.79  5.45i
 0.218i
 0.086  0.151i

I1  0.379

I2  0.218

I3  0.174
Находим токи методом контурных токов:
 Z1  Z2 Z2    50  7.54i 25  3.77i 
 

 Z2 Z2  Z3   25  3.77i 50  23.23i 
r  
 0.087  0.369i 

 0.086  0.151i 
1
e 
E
 
0
e  
J  r

J1  0.379
J1  J  0.087  0.369i
1
3
J2  J  J  1.241  10
1
2
 0.218i

J2  0.218

J3  0.174
J3  J  0.086  0.151i
2

Находим ток во
второй ветви методом эквивалентного генератора:
Z1
Uxx
E
Z2
Z3
Rg
Находим контурный ток.
j 
E
Z1  Z3
 0.115  0.247i
Напряжение холостого хода:
Uxx  E  j Z1  1.936  8.399i
Сопротивление генератора:
Rg 
( Z1 Z3)
Z1  Z3
 13.512  5.337i
Ток во второй ветви равен
Ikz2 


Ikz2  0.218
Uxx
Rg  Z2
3
 1.241  10
 0.218i
Z3
3. Строим лучевую диаграмму:
m  50
I1 
0
 I m
 1
I2 
0
 I m
 2
I3 
0




E


E  I R


1
U1 


E  I  R  i Xl1 I

1
1

 E  I  R  i Xl1 I  i I  Xm 
1
1
2

В
0
 I m
 3
0




I R

2

U2  

I  R  i Xl2 I
2
2


 I  R  i Xl2 I  i Xm I 
2
1 В
2
0


 I  Xc i 
U3  
3

 I  R  I  Xc i 
3
3
В
25
22
19
16
Im( I1)
Im( I2)
13
Im( I3)
Im( U1)
10
Im( U2)
7
Im( U3)
4
1
 15
 10
5
0
5
10
15
20
25
2
5
Re( I1) Re( I2) Re( I3) Re( U1) Re( U2) Re( U3)
4. Определяем
показание
электродинамического
аналитически и по топографической диаграмме.
Из графика:
V 
ReU32  ReU222  ImU32  ImU222
V  7.028
Аналитически находим напряжение на вольтметре(Uv):
Uv  I  Xc i  I  R Uv  7.028
3
2
вольтметра
5. Проверяем расчеты с помощью программы Electronics Workbench:
Вывод:
В ходе проделанной работы были изучены некоторые операции с комплексными числами,
рассчитаны токи во всех ветвях, ток в ветви с индуктивностью L2 методом эквивалентного
генератора, произведена развязка индуктивной связи. Все значения токов, рассчитанные
различными способами (в программе MathСad), совпали. Баланс мощностей сошелся, из чего
следует, что вычисления произведены верно.
В результате, были построены векторные диаграммы токов (лучевая) и напряжений
(топографическая). По последней мы определили показание электродинамического
вольтметра и сравнили его со значением, рассчитанным аналитически. Они совпадают, что
подтверждает правильность решения. Также, диаграмма подтверждает, что напряжение на
индуктивности опережает ток на 90 градусов, а на конденсаторе отстаёт на 90 градусов.
Все расчеты были подтверждены в программе Electronics WorkBench (с погрешностями), это
вызвано тем что программы EWB и MathCAD числа округляют по-разному.