Лабораторная работа №23. «Катушка индуктивности в цепи

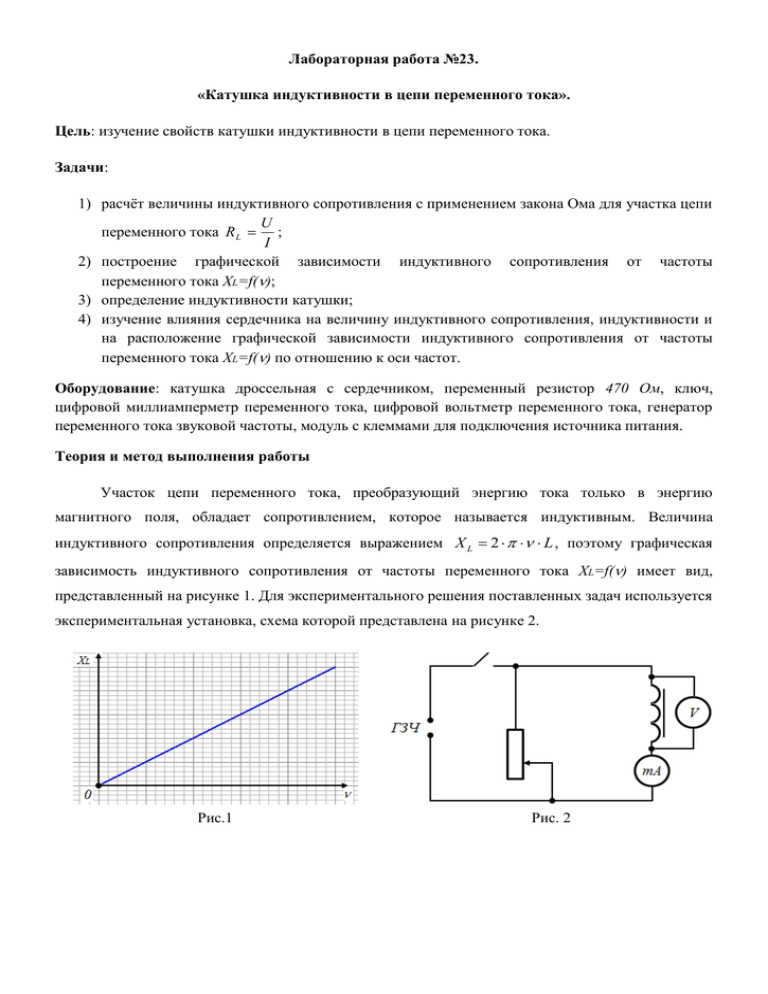
Лабораторная работа №23.
«Катушка индуктивности в цепи переменного тока».
Цель: изучение свойств катушки индуктивности в цепи переменного тока.
Задачи:
1) расчёт величины индуктивного сопротивления с применением закона Ома для участка цепи
U
переменного тока R L  ;
I
2) построение графической зависимости индуктивного сопротивления от частоты
переменного тока XL=f();
3) определение индуктивности катушки;
4) изучение влияния сердечника на величину индуктивного сопротивления, индуктивности и
на расположение графической зависимости индуктивного сопротивления от частоты
переменного тока XL=f() по отношению к оси частот.
Оборудование: катушка дроссельная с сердечником, переменный резистор 470 Ом, ключ,
цифровой миллиамперметр переменного тока, цифровой вольтметр переменного тока, генератор
переменного тока звуковой частоты, модуль с клеммами для подключения источника питания.
Теория и метод выполнения работы
Участок цепи переменного тока, преобразующий энергию тока только в энергию
магнитного поля, обладает сопротивлением, которое называется индуктивным. Величина
индуктивного сопротивления определяется выражением X L  2     L , поэтому графическая
зависимость индуктивного сопротивления от частоты переменного тока XL=f() имеет вид,
представленный на рисунке 1. Для экспериментального решения поставленных задач используется
экспериментальная установка, схема которой представлена на рисунке 2.
Рис.1
Рис. 2
Ход работы:
1. Собрать экспериментальную установку.
2. Подготовить таблицы результатов измерений и вычислений:
Катушка индуктивности с сердечником
Напряжение
U
=
3
В
Сила
тока
Частота
I

мА
Гц
Индуктивное
сопротивление
Индуктивность
катушки с
сердечником
RL
Ом
U
XL 
I
L
Гн
XL
L
2   
Абсолютная
погрешность
L
Гн
Li  Lср  Li
10
20
30
40
50
60
70
80
90
100
Среднее
Катушка индуктивности без сердечника
Напряжение
U
=
3
В
Сила
тока
Частота
I

мА
Гц
Индуктивное
сопротивление
Индуктивность
катушки с
сердечником
RL
Ом
U
XL 
I
L
Гн
XL
L
2   
10
20
30
40
50
60
70
80
90
100
Среднее
Абсолютная
погрешность
L
Гн
Li  Lср  Li
3. Включить генератор, замкнуть ключ, плавно увеличивая амплитуду выходного сигнала
генератора до тех пор, пока вольтметр переменного тока, подключенный к катушке
индуктивности, покажет напряжение 3 В.
4. Изменяя частоту выходного сигнала, показания миллиамперметра заносить в таблицу, для
случаев: 1) катушка индуктивности с сердечником; 2) катушка индуктивности без
сердечника.
U
5. Рассчитать индуктивное сопротивление, используя закон Ома для участка X L  .
I
6. Построить графические зависимости индуктивного сопротивления от частоты переменного
тока XL=f() для случаев: 1) катушка индуктивности с сердечником; 2) катушка
индуктивности
без сердечника.
Возможен
вариант
графической
обработки
экспериментальных данных и вычислений в Microsoft Excel с работой мастером диаграмм и
добавлением линии тренда (линейная зависимость, пересечением в начале координат и
указанием уравнения прямой, угловой коэффициент которой позволяет рассчитать
величину индуктивности катушки).
7. Индуктивность катушки с сердечником и без сердечника рассчитать по формуле
XL
L
.
2   
8. Изучить влияние сердечника на величину индуктивности.
9. Изучить влияние сердечника на расположение графической зависимости индуктивного
сопротивления от частоты переменного тока XL=f() по отношению к оси частот. Для этого
построить графические зависимости индуктивного сопротивления от частоты переменного
тока XL=f() в одной системе координат и сформулировать вывод. Обосновать результат
влияния сердечника на расположение графической зависимости индуктивного
сопротивления от частоты переменного тока XL=f() по отношению к оси частот.
10. Сформулировать общий вывод по лабораторной работе.