001501-28
реклама

Шифр: 001501-28
Задание согласно варианту представлено в таблице:
Номер ветви
1
2
3
4
5
6
7
8
Начало конец
54
43
31
12
26
65
35
42
Сопротивления
420
110
410
860
830
440
280
790
Источники
ЭДС, В
0
500
0
0
300
0
0
0
Источники
тока, А
0
0
0
0
7
8
0
0
Составить баланс мощностей.
МЭГ напряжения найти ток сопротивления R2.
Найти напряжение между узлами 6 и 4 (U64).
Решение
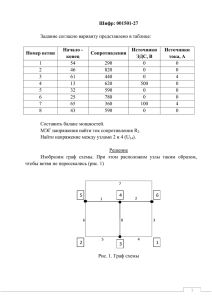
Изобразим граф схемы. При этом расположим узлы таким образом,
чтобы ветви не пересекались (рис. 1)
7
5
1
6
6
4
3
2
8
5
3
4
2
1
Рис. 1. Граф схемы
1
Включим в ветви цепи сопротивления и источники ЭДС. Источники
тока подключаем параллельно соответствующим ветвям (рис.2).
Расчёт токов методом преобразования
На схеме (рис.2) преобразуем источник тока J05 в источник напряжения
E05:
𝐸05 = 𝐽05 ∙ 𝑅5 = 7 ∙ 830 = 5810 (В),
а источник тока J06 в источник напряжения E06:
𝐸06 = 𝐽06 ∙ 𝑅6 = 8 ∙ 440 = 3520 (В)
R7
I7
R1
I1
5
E2
R2
4
3
I2
R6
R3
R8
J06
I3
I6
I8
R5
I5
6
J05
E5
I4
2
R4
1
Рис. 2. Схема цепи.
Полученная схема показана на рисунке 3. На этой схеме источник
напряжения E5 , E05 и E06 объединены в источник напряжения 𝐸56 :
𝐸56 = 𝐸5 + 𝐸05 + 𝐸06 = 300 + 5810 + 3520 = 9630 (В),
а последовательно включённые сопротивления 𝑅3 и 𝑅4 , 𝑅5 и 𝑅6 .
𝑅34 = 𝑅3 + 𝑅4 = 410 + 860 = 1270 (Ом);
2
𝑅56 = 𝑅5 + 𝑅6 = 830 + 440 = 1270 (Ом);
R7
I7
R1
I1
5
E2
R2
4
3
I2
R56
R34
R8
I3
E56
I’6
I8
I4
I’5
6
1
2
Рис. 3. Преобразованная схема цепи.
Чтобы сделать треугольник 5-4-2 пассивным, преобразуем источник
напряжения 𝐸56 в источник тока 𝐽56 :
𝐽56 =
𝐸56 9630
=
= 7.583 (𝐴)
𝑅56 1270
Пассивный треугольник 5-4-2 преобразуем в пассивную звезду (рис.4),
где
𝑅1 ∙ 𝑅56
= 215.081 (Ом)
𝑅1 + 𝑅56 + 𝑅8
𝑅1 ∙ 𝑅8
𝑅18 =
= 133.79 (Ом)
𝑅1 + 𝑅56 + 𝑅8
𝑅8 ∙ 𝑅56
𝑅856 =
= 404.556 (Ом)
𝑅1 + 𝑅56 + 𝑅8
𝑅156 =
R1
I1
1
R8
R18
R56
I8
J56
R156
R856
J56
2
3
Рис.4. Преобразование «треугольник-звезда».
Источник тока 𝐽56 преобразуем в источники напряжения:
𝐸156 = 𝐽56 ∙ 𝑅156 = 7.583 ∙ 215.081 = 1631 (В)
𝐸856 = 𝐽56 ∙ 𝑅856 = 7.583 ∙ 404.556 = 3068 (В)
В результате этих преобразований схема будет иметь следующий вид,
представленный на рисунке 5.
R156
E156
R18
4
0
R856
E856
R7
I7
5
E2
I2
R2
3
R34
2
I3
Рис. 5. Преобразованная схема цепи
С целью дальнейшего упрощения схемы объединим сопротивления:
𝑅7′ = 𝑅7 + 𝑅156 = 495.081 (Ом)
𝑅2′ = 𝑅18 + 𝑅2 = 243.79 (Ом)
′
𝑅34
= 𝑅856 + 𝑅34 = 1675 (Ом)
Теперь схема имеет следующий вид (рис.6):
E156
R’7
0
E2
R’2
R’34
I7
I2
3
E856
I3
4
Рис. 6. Преобразованная схема цепи
Далее целесообразно использовать метод узловых напряжений. Для
определения напряжения 𝑈03 необходимо составить одно уравнение:
1
1
1
𝐸856 𝐸2
𝐸156
𝑈03 ∙ ( ′ + ′ + ′ ) = ′ − ′ − ′
𝑅7 𝑅2 𝑅34
𝑅34
𝑅2
𝑅7
𝑈03 =
𝐸856 𝐸2
𝐸
− ′ − 156
′
𝑅34
𝑅2
𝑅7′
1
1
1
( ′ + ′ + ′ )
𝑅7 𝑅2 𝑅34
= −522.885 (В)
Определим токи на рисунке 6 на основании второго закона Кирхгофа:
−𝐸156 − 𝑈03
𝑈03 = −𝐼7 𝑅7′ − 𝐸156 ;
𝐼7 =
= −2.238 (А)
𝑅7′
𝐸2 + 𝑈03
′
𝑈03 = 𝐼2 𝑅22
−𝐸2 ;
𝐼2 =
= −0.094 (А)
′
𝑅22
𝐸856 − 𝑈03
′
𝑈03 = 𝐸856 − 𝐼3 𝑅34
;
𝐼3 =
= 2.144 (А)
′
𝑅34
Запишем уравнение по второму закону Кирхгофа для контура 4-3-1-2
(рис. 3):
𝐼2 𝑅2 − 𝐼8 𝑅8 + 𝐼3 (𝑅3 + 𝑅4 ) = 𝐸2 ,
Отсюда ток 𝐼8 равен:
𝐼8 =
𝐼2 𝑅2 + 𝐼3 (𝑅3 + 𝑅4 ) − 𝐸2
= 2.801 (А).
𝑅8
Для определения тока 𝐼5 составим уравнение по первому закону
Кирхгофа (рис. 2) для узла 2:
𝐼5 = 𝐼8 + 𝐼3 − 𝐽05 = −2.055 (А),
Для определения неизвестных токов 𝐼1 , 𝐼6 , составим уравнение по
первому закону Кирхгофа (рис. 2) для узлов 4, 5:
5
для узла 4
для узла 5
𝐼1 = 𝐼2 + 𝐼8 = 2.707 (А),
𝐼6 = 𝐼1 − 𝐽06 − 𝐼7 = −3.055(А),
Составление баланса мощностей.
ЭДС положительна при совпадающих направлениях ЭДС и тока ветви и
отрицательна при противоположном направлении ЭДС и тока ветви.
Мощность источника тока определяется произведением тока данного
источника и напряжения на его зажимах. Она положительна при
противоположных направлениях на зажимах источника тока и тока источника.
Мощность, выделяемая в активных сопротивлениях, всегда положительна
и равна:
𝐼 2 𝑅 = 𝑃.
Баланс мощности записывается в виде 𝑃ист = 𝑃пр :
𝑓
𝑛
2
∑𝑚
𝑖=1 𝐸𝑖 𝐼𝑖 + ∑𝑘=1 𝐽𝑘 𝑈𝑘 = ∑𝑙=1 𝑅𝑙 𝐼𝑙 ,
где
m - число источников ЭДС в схеме;
n - число источников тока в схеме;
f - число активных сопротивлений в схеме.
Составим баланс мощностей для схемы рис. 2:
𝑈62 = 𝐸5 − 𝐼5 𝑅5 = 2.006 ∙ 103 (В),
𝑈56 = −𝐼6 𝑅6 = 1.344 ∙ 103 (В),
𝑃ист = 𝐸5 𝐼5 + 𝐸2 𝐼2 + 𝐽05 𝑈62 + 𝐽06 𝑈56 = 2.413 ∙ 104 (Вт),
𝑃пр = 𝐼12 𝑅1 + 𝐼22 𝑅2 + 𝐼32 (𝑅3 + 𝑅6 ) + 𝐼52 𝑅5 + 𝐼62 𝑅6 + 𝐼72 𝑅7 + 𝐼82 𝑅8 =
= 2.413 ∙ 104 (Вт)
Так как мощность источников равна мощности тепловых потерь, то
значения рассчитанных токов верны.
6
Определение напряжения 𝑈64 .
Для определения напряжения 𝑈64 воспользуемся рисунком 2. Тогда на
основании второго закона Кирхгофа можно записать:
𝜑6 = 𝜑4 + 𝐼1 𝑅1 + 𝐼6 𝑅6 .
Отсюда
𝑈64 = 𝜑6 − 𝜑4 = 𝐼1 𝑅1 + 𝐼6 𝑅6 = −207.183 (В).
Определение тока в резисторе 𝑅2 методом эквивалентного генератора
Метод эквивалентного генератора используется для исследования
работы какого-либо участка в сложной электрической цепи.
Разделим электрическую цепь на две части: эквивалентный генератор и
потребитель (рис. 7).
R2
2
I2
5
Eэ
Rэ
Рис. 7. Эквивалентная схема замещения
На схеме (рис.7) искомый ток 𝐼2 определим по закону Ома для
замкнутой цепи:
𝐼2 =
𝐸э
,
𝑅2 + 𝑅э
где
𝐸э - ЭДС эквивалентного генератора, величину которой определяют как
напряжение на зажимах генератора в режиме холостого хода (𝐸э = 𝑈хх );
𝑅э - внутреннее сопротивление эквивалентного генератора, величину
которого определяют как эквивалентное сопротивление пассивного
двухполюсника относительно исследуемых зажимов.
7
Для определения напряжения на зажимах генератора в режиме холостого
хода исключим из рассматриваемой цепи (рис. 2) ветвь, содержащую
сопротивление R2, и представим остальную часть цепи (режим холостого хода):
R7
I7
R1
4
I1
5
Uxx
E2
R6
3
I2
R3
R8
J06
I6
R5
I5
I3
II
III
I8
E4
I5
6
J05
2
R4
1
Рис. 8. Схема для расчета 𝐸э
Методом контурных токов определим токи в ветвях схемы. Составим
уравнения по второму закону Кирхгофа относительно контурных токов (рис.8):
{
(𝑅7 + 𝑅3 + 𝑅4 + 𝑅8 + 𝑅1 )𝐼𝐼 − (𝑅1 + 𝑅8 )𝐼𝐼𝐼 = 0
(𝑅5 + 𝑅6 + 𝑅1 + 𝑅8 )𝐼𝐼𝐼 − (𝑅1 + 𝑅8 )𝐼𝐼 − 𝐽05 𝑅5 − 𝐽06 𝑅6 = 𝐸5
Отсюда:
𝐼𝐼 = 2.166(А),
𝐼𝐼𝐼 = 4.94 (А).
Тогда токи в ветвях схемы равны:
𝐼07 = −𝐼𝐼 = −2.166 (А);
𝐼01 = 𝐼𝐼𝐼 − 𝐼𝐼 = 2.774 (А);
Знание токов 𝐼07 , 𝐼01 позволяет определить напряжение холостого хода:
𝑈хх = −𝐼07 𝑅7 − 𝐼01 𝑅1 + 𝐸2 = −58.754 (В).
8
Для расчёта внутреннего сопротивления эквивалентного генератора
необходимо преобразовать активный двухполюсник (рис. 8) в пассивный, при
этом источники ЭДС закорачиваются, а источники тока размыкаются:
R7
R1
5
4
Rэ
R6
3
R8
R3
R5
6
1
R4
Рис.9. Схема для расчета 𝑅э
Необходимо найти сопротивление между точками 4 и 3.
Заменим треугольник резисторов 𝑅1 𝑅56 , и 𝑅8 звездой. Схема замещения
представлена на рисунке 10.
R156
Rэ
0
R7
R18
R34
3
R856
Рис. 10. Схема замещения треугольника звездой
Сопротивления 𝑅156 , 𝑅18 , 𝑅856 равны:
𝑅1 ∙ 𝑅56
= 215.081 (Ом)
𝑅1 + 𝑅56 + 𝑅8
𝑅1 ∙ 𝑅8
=
= 133.79 (Ом)
𝑅1 + 𝑅56 + 𝑅8
𝑅156 =
𝑅18
9
𝑅856 =
𝑅8 ∙ 𝑅56
= 404.556 (Ом)
𝑅1 + 𝑅56 + 𝑅8
Тогда
𝑅э = 𝑅18 +
(𝑅156 + 𝑅7 )(𝑅856 + 𝑅34 )
= 515.901 (Ом).
𝑅156 + 𝑅7 + 𝑅856 + 𝑅34
Зная 𝐸э = 𝑈хх и 𝑅э , найдем ток исследуемой ветви:
𝐼02 =
𝐸э
= −0.094 (А).
𝑅2 + 𝑅э
Построение потенциальной диаграммы.
Для построения потенциальной диаграммы необходимо знать
напряжение на всех элементах контура, а также сопротивления всех элементов
контура. На рис. 11 показан контур, для которого мы будем строить
потенциальную диаграмму.
R1
I1
5
4
E06
R8
7
I6
R6
I8
E55
6
1
I5
R5
2
Рис. 11. Контур для построения потенциальной диаграммы
Базисную точку выберем произвольно, например точку 5. Построение
будем производить, обходя контур по часовой стрелке.
Определим потенциалы точек:
𝜑4 = 𝜑5 − 𝐼1 𝑅1 = −1137 (В);
𝜑2 = 𝜑4 − 𝐼8 𝑅8 = −3350 (В);
𝜑1 = 𝜑2 − 𝐼5 𝑅5 = −7454 (В);
10
𝜑6 = 𝜑1 + 𝐸5′ = −1344 (В);
𝜑7 = 𝜑6 − 𝐼6 𝑅6 = −3520 (В);
𝜑5 = 𝜑7 + 𝐸06 = 0 (В);
По оси абсцисс будем откладывать значения сопротивлений элементов,
а по оси ординат – значения потенциалов точек. Базисную точку помещаем в
начало координат (рис.12).
5
250
500
750
1000
1250
1500
1750
2000
2250
2500
R(Ом)
5
0
-1
4
6
-2
-3
2
7
-4
-5
-6
-7
1
-8
U(В)х103
Рис. 12. Потенциальная диаграмма
Результаты расчетов представим в виде таблицы:
Rэ,
Р, Вт
I3 , А
I4 , А
I5 , А
2.707 -0.094 2.144
2.144
-2.055 -3.055 -2.238 2.801 -207.183 -58.754 515.901 24130
I1 , А
I2 , А
I6 , А
I7 , А I8 , А U64 ,В
Uхх , В
Ом
11
Литература
1. Ю.Г.Толстов, А.А. Теврюков: Теория электрических цепей. Москва: 1970;
2. Башарин С.А., Федоров В. А.: Теоретические основы электротехники.
Теория электрических цепей и электромагнитного поля. Москва: 2004г.
3. Методическая разработка БГУИР.
4. Интернет
12