Lekciya9
реклама

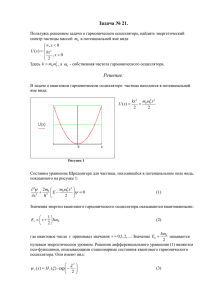
Лекция 9 Гармонический осциллятор. Уровни энергии и волновые функции (решение в виде ряда) Одномерным гармоническим осциллятором называется частица, движущаяся в потенциале U ( x) m 2 x 2 / 2 , где m - масса частицы, - число, имеющее размерность сек-1 (в случае классического движения частицы в указанном потенциале величина имела бы смысл круговой частота колебаний частицы). Найдем волновые функции и энергии стационарных состояний осциллятора. Стационарное уравнение Шредингера для осциллятора имеет вид d 2 f ( x) m 2 x 2 f ( x) Ef ( x) 2m dx 2 2 2 (1) От координаты x и энергии E перейдем к безразмерным переменным и , используя величины и m (2) имеющие размерности длины и энергии соответственно: m x 2 В новых переменных уравнение Шредингера (1) принимает вид d 2 f ( ) 2 f ( ) 0 d 2 (3) Необходимо найти такие значения (и, следовательно, E ), при которых уравнение (3) имеет конечные при всех решения и сами эти решения. Перейдем к новой неизвестной функции u ( ) : f ( ) u ( )e 2 2 (4) Подставляя это выражение в (3), получим уравнение для неизвестной функции u ( ) : u( ) 2 u( ) ( 1)u ( ) 0 (5) Ищем решение уравнения (5) в виде степенного ряда u ( ) Ck k k 0 где Ck - неизвестные коэффициенты. Подставляя ряд (6) в уравнение (5), получим 1 (6) k (k 1)C k 2 k k 2 k 0 k 0 2 kCk k ( 1) Ck k 0 (7) Меняя в первом слагаемом индекс суммирования k k 2 и собирая одинаковые степени , найдем рекуррентное соотношение для коэффициентов ряда (6) Ck 2 2k 1 Ck (k 1)(k 2) (8) Таким образом, чтобы ряд (6) определял решение уравнения (5) его коэффициенты должны быть связаны рекуррентным соотношением (8). При этом, поскольку соотношение (8) связывает Ck и Ck 2 , оно связывает отдельно четные и нечетные коэффициенты. Поэтому C0 и C1 могут быть выбраны произвольно (заметим, что отсюда следует, что ряд (6), (8) определяет общее решение уравнения (3)). В частности, ряды с C0 1 и C1 0 (то есть ряд по четным степеням ) и C0 0 и C1 1 (то есть ряд по нечетным степеням) определяют два линейно независимых частных решения уравнения (5)). Чтобы понять, какой функции отвечает ряд Тейлора (6), (8), рассмотрим соотношение (8) при больших k . Для больших k рекуррентное соотношение (8) имеет вид (мы пренебрегли числами порядка единицы по сравнению с большим k ): Ck 2 2 Ck k (9) Соотношение (9) для четных индексов отвечает разложению в ряд Тейлора функции exp 2 и exp 2 - для нечетных. Это значит, что при больших (при которых сумма ряда (5) определяется слагаемыми c большими k ) оба частных решения уравнения (5) содержат экспоненту exp 2 . Поэтому соответствующие частные решения уравнения (1) f ( ) расходятся при . Однако при некоторых значениях энергии ряд (6) обрывается, и все коэффициенты, начиная с некоторого, равны нулю. Действительно, из (7) следует, что если 2n 1 , где n любое целое неотрицательное число (или E (n 1/ 2) ), то коэффициент Cn 2 обращается в нуль. Очевидно, в этом случае будут равны нулю и коэффициенты Cn 4 , Cn 6 , ... . Поэтому в этом случае ряд (6) содержит конечное число слагаемых той же четности, что и слагаемое Cn n .. Таким образом, если 2n 1 , то одно из частных решений уравнения (5) сводится к многочлену определенной четности, а не 2 к функции exp 2 , и, следовательно, соответствующее ограниченной частное функцией E (n 1/ 2) и решение при всех f ( ) u ( ) exp 2 / 2 , уравнения (1), значениях координат. Следовательно, является указанные f ( ) являются собственными значениями и собственными функциями уравнения (1). Найдем явно несколько первых решений. При E / 2 ( n 0 ), обрыв ряда происходит при переходе от нулевого коэффициента ко второму. То есть в этом случае коэффициент C2 0 . Ряд же по нечетным степеням при таком значении E не обрывается, и потому его нужно сделать равным нулю, взяв коэффициент C1 0 . Поэтому функция u ( ) в этом случае многочлен нулевой степени. Таким образом, значение E0 / 2 - минимальное собственное значение, которому отвечает собственная функция f 0 ( ) C0 exp 2 / 2 (10) Следующее значение энергии, при котором происходит обрыв ряда (6) E 3 / 2 ( n 1 ). В этом случае обращается в нуль коэффициент C3 . Ряд по четным степеням надо сделать тождественно равным нулю, выбрав C0 0 . Таким образом, E1 3 / 2 f1 ( ) C1 exp 2 / 2 (11) Аналогично из соотношения (8) найдем E2 3 / 2 f 2 ( ) C0 (1 2 2 ) exp 2 / 2 (12) и т.д. Отметим, что из приведенных выше рассуждений буквально не следует, что перечисленные собственные решения исчерпывают все собственные значения и собственные функции уравнения (1). Действительно, так как линейная комбинация двух неограниченно возрастающих функций может, вообще говоря, расходиться гораздо медленнее каждой функции, то можно было бы ожидать, что при некоторых значениях E (n 1/ 2) определенная линейная комбинация четного и нечетного частных решений уравнения (4) будет расходится медленнее, чем exp 2 / 2 , и, следовательно, такие значения E будут собственными значениями уравнения (1). Это, однако, невозможно одновременно как на , так и на . Предлагаем слушателям доказать это утверждение самостоятельно при домашней подготовке к следующей лекции. Таким образом, собственные значения и собственные функции осциллятора имеют вид 3 f n ( ) An H n ( ) exp 2 / 2 En (n 1/ 2) n 0,1, 2,... (13) где H n ( ) - многочлены n -ой степени, которые называются полиномами Эрмита. При принятой в математике нормировке полиномы Эрмита отличаются множителями от многочленов (10)(12), а постоянные An равны An 1 (15) 2 n! n Как следует из проведенного выше вывода, полиномы Эрмита с четными индексами содержат только четные степени , с нечетными - нечетные. Это значит, что собственные функции, отвечающие четным уровням энергии (нулевому, второму и т.д.) являются четными функциями координаты, нечетным уровням (первому, третьему и т.д.) - нечетными. Этот вывод согласуется с общим утверждением о четности собственных функций оператора Гамильтона в случае четной потенциальной энергии. Приведем в заключение несколько нормированных собственных функций одномерного гармонического осциллятора f 0 ( ) 4 f1 ( ) f 2 ( ) 1 2 4 exp 2 / 2 (16) exp 2 / 2 (17) 1 2 2 1 exp 2 / 2 4 2 (18) Знание собственных значений и собственных функций гамильтониана гармонического осциллятора (13) позволяет находить вероятности различных значений энергии осциллятора и его среднюю энергию в любых состояниях, а также строить все возможные волновые функции осциллятора в любые моменты времени. Например. Пусть в момент времени t 0 нормированная волновая функция гармонического осциллятора имеет вид ( x, t 0) 2 2 exp 2 / 2 4 5 m x (19) Какие значения может принимать энергия осциллятора в последующие моменты времени и с какими вероятностями? Найти среднюю энергию гармонического осциллятора как функцию времени. Какова средняя четность указанного состояния осциллятора? Как средняя четность зависит от времени? 4 Поскольку потенциальная энергия не зависит от времени, вероятности различных значений энергии осциллятора в любом состоянии не зависят от времени. Поэтому достаточно вычислить вероятности различных значений энергии и среднюю энергию осциллятора в момент времени t 0 . Чтобы найти эти величины для осциллятора в рассматриваемом состоянии разложим начальную волновую функцию этого состояния по собственным функциям оператора Гамильтона для гармонического осциллятора. Так как данная в условии задачи волновая функция представляет собой произведение многочлена второй степени на exp 2 / 2 , то в разложении могут быть представлены только нулевая, первая и вторая собственные функции гамильтониана осциллятора. Используя явные выражения для трех первых собственных функций осциллятора (16)-(18), легко найти ( x, t 0) 1 2 2 f 0 ( ) f1 ( ) f 2 ( ) 5 5 5 (20) Поэтому энергия осциллятора, находящегося в рассматриваемом состоянии может принимать значения E0 / 2 , E1 3 / 2 и E2 5 / 2 с вероятностями w0 1/ 5 , w1 2 / 5 , w2 2 / 5 .. Среднюю энергию осциллятора найдем по формуле теории вероятностей для математического ожидания E En wn (21) n Так как собственные функции оператора Гамильтона f 0 ( ) и f 2 ( ) являются четными, то они являются и собственными функциями оператора четности, отвечающими собственному значению p 1 , f1 ( ) - собственной функцией оператора четности, отвечающей собственному значению p 1 . Поэтому вероятность обнаружить четность рассматриваемого состояния осциллятора, равную +1, есть w 3/ 5 , равную -1, - w 2 / 5 . Отсюда найдем, что средняя четность рассматриваемого состояния равна p 1 5 (22) Разумеется, вычисление средней четности данного состояния по квантовомеханической формуле приводит к тому же результату. Предоставляем слушателям самостоятельно в этом убедиться. Вероятности различных значений четности и средняя четность от времени не зависят, так как оператор Гамильтона и оператор четности коммутируют. В том, что средняя четность не зависит от времени можно убедиться и непосредственно. Для этого нужно построить волновую функцию осциллятора в любые моменты времени по 5 начальной волновой функции (20) (используя формулу для общего решения временного уравнения Шредингера) а затем вычислить среднюю четность по квантовомеханической формуле для средних. Предлагаем слушателям проделать эти вычисления самостоятельно. 6