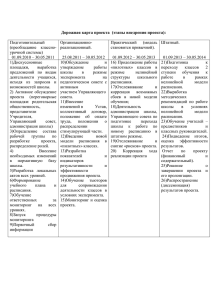
2.4.14. Расчет динамических расписаний
реклама

2.4.14. Расчет динамических расписаний Различают расписания статические и динамические. Статическое расписание составляют в окончательном виде до начала его реализации, т.е. заранее должны быть известны совокупности предстоящих работ и средства (ресурсы) для их выполнения. Задачи синтеза статических расписаний имеют ряд разновидностей. Большинство из них относится к NP-трудным задачам дискретного математического программирования, что при размерах задач, имеющих место на практике, исключает возможность применения точных методов оптимизации. Поэтому существующие методы синтеза расписаний являются приближенными, причем они ориентированы на статические расписания. Однако статические расписания оказываются далекими от оптимальных, если в процессе их исполнения возникают отклонения от использованных при расчете исходных данных. Поэтому целесообразно применять расписания, способные адаптироваться к изменяющимся условиям. Такие расписания будем называть динамическими или адаптируемыми. Синтез динамических расписаний, или, точнее, адаптация расписаний к изменяющимся условиям, представляет собой слабо исследованную проблему. Рассмотрим возможный подход к решению задачи синтеза динамических расписаний [64]. Эта задача решается, если возникают заметные отклонения реальных значений параметров процесса от значений, априорно принятых при расчете исходного расписания, т.е. расписания, рассчитанного до начала реализации процесса. Во-первых, отклонения могут быть обусловлены неточностью исходных данных вследствие естественного разброса параметров процесса (производительностей серверов). Такие отклонения обычно представляются действительными переменными Dj, их можно выразить в процентах относительно исходных номинальных значений. Во-вторых, отклонения могут вызываться непредвиденными событиями, влияющими на протекание процесса. Типичными примерами таких событий служат внезапные изменения производительности серверов (например, их отказ) или числа требующих обслуживания работ. В таких случаях событием является скачкообразное изменение параметров задачи, фиксируемое в момент их изменения τ. Если переменные Dj выявляются в момент времени т, то начало их учета также будем относить к событиям, т.е. событие - это суммарное (накопленное) изменение параметров, фиксируемое в некоторый момент τ. В соответствии с этими двумя типами событий целесообразно при исследовании использовать два типа тестовых задач. В задачах первого типа Q1 имитируется резкое снижение производительности одного из серверов в момент времени т. В задачах второго типа Q2 имитируются случайные отклонения времен обслуживания всех работ на всех серверах в пределах заданного относительного допуска ∆. Выделим в системе управления процессом две части: решатель, предназначенный для расчета и корректировки расписания, и исполнитель, управляющий реализацией расписания и фиксирующий события. Возможны два подхода к реализации синтезированного расписания. В соответствии с первым подходом, обозначаемым далее А1, к исполнителю поступает хромосома С, рассчитанная решателем, например, с помощью НСМ (ее можно назвать квазиоптимальной), т.е. исполнитель получает последовательность правил, определяющих расписание S. Во втором подходе, обозначаемом А2, решатель сначала рассчитывает с помощью оптимизационного алгоритма хромосому С и далее по этой хромосоме определяет и передает исполнителю само расписание S, т.е. непосредственно данные о месте и последовательности выполнения работ. Если т - момент совершения события, tрасч - продолжительность расчета при обновлений (корректировке) расписания и если пренебречь задержками в передаче данных между исполнителем и решателем, то скорректированное расписание поступит к исполнителю в момент времени τ + tрасчч. При этом на интервале времени [τ, τ + tрасчч] управление процессом приходится осуществлять по исходным расписанию S или хромосоме С, уже не являющимися квазиоптимальными. Этот интервал времени назовем латентным (или временным зазором), а число актов процесса, приходящееся на латентный интервал, - длиной латентного участка хромосомы В. Здесь под актом понимается начало обслуживания одной работы на одном сервере. Очевидно, что синтез динамических расписаний возможен только в том случае, если tnpw> tрасч, где tпроц продолжительность процесса. Поэтому далее рассматриваются ситуации, при которых инерционность процесса выше, чем инерционность расчета расписаний. Для выработки рекомендаций по расчету динамических расписаний нужно, во-первых, определить условия, при которых предпочтительным оказывается подход А1 или подход А2, и, во-вторых, выяснить степень влияния длительности tрасч и связанного с ней латентного участка хромосомы на точность синтеза скорректированного расписания. При этом достигнутая на j-м шаге точность скорректированного расписания характеризуется величиной δj относительной погрешностью целевой функции, определяемой как δj = (Fj - Fmin ) /Fmin (2.7) где Fj- значение целевой функции на j-м шаге оптимизационного алгоритма; Fmin- оптимальное значение целевой функции. Качество динамического расписания, т.е. расписания, которому подчиняется управляемый процесс, характеризуется его близостью к оптимальному расписанию. Отметим, что при t >τ, где t - текущее время, динамическое расписание состоит из двух частей, одна часть относится к латентному участку, другая к участку после τ + tрасч, т.е. представляет собой скорректированное расписание. Погрешность, обусловливаемую латентным участком, можно снизить, уменьшая длину этого участка. Погрешность, обусловливаемая второй частью, уменьшается при увеличении объема вычислений, выполненных обычным генетическим методом или НСМ, т.е. при увеличении В. Отметим, что объем вычислений характеризуется числом оценок N целевой функции или временем tрасч, затраченным на расчет, tрасч = tш N, где tш - машинное время на однократный расчет целевой функции. Следовательно, в каждом конкретном случае можно говорить об оптимальном выборе параметра В. К сожалению, практический расчет оптимального В в реальных процессах затруднен ввиду неопределенности ряда влияющих факторов, таких, как характер и величина дестабилизирующего изменения параметров, разброс результатов решения задач генетическим методом, неизвестность значения Fmin. Поэтому целесообразно говорить лишь о рекомендациях по выбору В. Они основаны на знании характера зависимостей погрешностей δj от tрасч и от В. Данные табл. 2.7 приведены для сравнения подходов А1 кА2. Рассчитывались погрешности, возникающие вследствие неучета разброса производительностей серверов в задаче N105, задаваемого в пределах допуска Д, т.е. рассматривалась задача типа Q2. Было проведено восемь серий, различающихся значениями Д, в каждой серии было выполнено по 14 экспериментов со случайными значениями производительностей. В таблице использованы обозначения: п, - для числа опытов, в которых подход А1 давал лучшее значение целевой функции, чем подход А2; пг -для числа опытов, в которых подходЛ2 давал лучшее значение целевой функции, чем подход А\;п}- для числа опытов, в которых лучшее значение целевой функции оказывалось у хромосомы со случайными значениями генов. Таблица 2,7 ∆,% n1 n2 N3 13 N3N3" 0 % 10 "i 1 2N2N 20 4 10 4 2»2 з 30 8 6 6 40 14 0 3 50 13 1 4 60 14 0 5 70 14 0 6 80 14 0 7