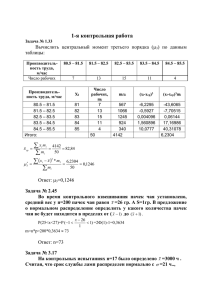
* По данный таблицы 2 вычислить коэффициент асимметрии
реклама

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И
ИНФОРМАТИКИ
В.С.Мхитарян, Л.И.Трошин, Е.В.Астафьева
ЗАДАЧНИК ПО СТАТИСТИЧЕСКОЙ ОЦЕНКЕ
ПАРАМЕТРОВ И ПРОВЕРКЕ ГИПОТЕЗ
(Для самостоятельной работы студентов)
В.С.Мхитарян, Л.И.Трошин, Е.В.Астафьева Задачник по
статистической оценке параметров и проверке гипотез /
Московский государственный университет экономики,
статистики и информатики.
Задачник содержит решения типовых примеров, а также задачи и варианты
заданий для самостоятельной работы студентов МЭСИ всех специальностей по курсу
“Теория вероятностей и математическая статистика”.
2
1.1.Вариационный ряд средней дневной выработки рабочих цеха приведен в таблице.
Вычислить коэффициент вариации V S , приняв i 0 .
Средняя дневная
выработка (руб.)
Число рабочих
102+i 104+i
2
104+i 106+i
8+2i
106+i 108+i
15+i
108+i 110+i
12
110+i 112+i
3+2i
1.2. По данным задачи 1.1. вычислить моду ( Mo ), приняв i 0 .
1.3. По данным задачи 1.1. вычислить центральный момент третьего порядка ( 3 ),
приняв i 1 .
1.4.По данным задачи 1.1. вычислить коэффициент асимметрии ( Ac ), приняв i 2 .
1.5.По данным задачи 1.1. вычислить коэффициент вариации ( VS ), приняв i 3 .
1.6.По данным задачи 1.1. вычислить медиану ( Me ), приняв i 2 .
1.7.Ряд распределения заработной платы рабочих механического цеха приведен в
таблице. Требуется вычислить коэффициент вариации V S , приняв i 1 .
Заработная
плата (руб.)
Число рабочих
211+i 213+i
7
213+i 215+i
10+2i
215+i 217+i
11+i
217+i 219+i
9
219+i 221+i
3+2i
1.8.По данным задачи 1.7. вычислить моду ( Mo ), приняв i 2 .
1.9. По данным задачи 1.7. вычислить центральный момент третьего порядка ( 3 ),
приняв i 0 .
1.10. По данным задачи 1.7.
i 2.
вычислить коэффициент асимметрии ( Ac ), приняв
1.11. По данным задачи 1.7. вычислить медиану ( Me ), приняв i 0 .
1.12. По данным задачи 1.7. вычислить коэффициент вариации ( VS ), приняв i 3 .
1.13. На основании вариационного ряда распределения длины плунжеров,
полученного по результатам статистического контроля, вычислить коэффициент
вариации V S , приняв i 0 .
Длина плунжера
(мм.)
Число плунжеров
80,5+2i 81,5+2i
2+2i
81,5+2i 82,5+2i
8
82,5+2i 83,5+2i
18+i
83,5+2i 84,5+2i
9+2i
1.14. По данным задачи 1.13. вычислить моду ( Mo ), приняв i 2 .
3
84,5+2i 85,5+2i
3
1.15. По данным задачи 1.13. вычислить центральный момент третьего порядка ( 3 ),
приняв i 1 .
1.16. По данным задачи 1.13. вычислить коэффициент асимметрии ( Ac ), приняв
i 0.
1.17. По данным задачи 1.13. вычислить медиану ( Me ), приняв i 1 .
1.18. По данным задачи 1.13. вычислить коэффициент вариации ( VS ), приняв i 3 .
1.19. По данным ряда распределения средней дневной выработки рабочих кузнечного
цеха вычислить коэффициент вариации V S , приняв i 0 .
Средняя дневная
выработка (руб.)
Число рабочих
98+i 100+i
2+i
100+i 102+i
12+i
102+i 104+i
20
104+i 106+i
5+2i
106+i 108+i
1+i
1.20. По данным задачи 1.19. вычислить моду ( Mo ), приняв i 0 .
1.21. По данным задачи 1.19. вычислить центральный момент третьего порядка ( 3 ),
приняв i 1 .
1.22. По данным задачи 1.19. вычислить коэффициент асимметрии ( Ac ), приняв
i 2.
1.23. По данным задачи 1.19. вычислить медиану ( Me ), приняв i 2 .
1.24. По данным задачи 1.19. вычислить коэффициент вариации ( VS ), приняв i 3 .
1.25. По результатам анализа температуры в хлебопекарной печи, представленным в
виде вариационного ряда, вычислить дисперсию, приняв i 0 .
Температура в
печи (0С)
Число замеров
201,5+i 202,5+i
3+i
202,5+i
-203,5+i
12+i
203,5+i 204,5+i
15+i
204,5+i 205,5+i
8
205,5+i 206,5+i
2+i
1.26. По данным задачи 1.25. вычислить моду ( Mo ), приняв i 2 .
1.27. По данным задачи 1.25. вычислить центральный момент третьего порядка ( 3 ),
приняв i 0 .
1.28. По данным задачи 1.25. вычислить коэффициент асимметрии ( Ac ), приняв
i 2.
1.29. По данным задачи 1.25. вычислить коэффициент вариации ( VS ), приняв i 1 .
1.30. По данным задачи 1.25. вычислить центральный момент третьего порядка ( 3 ),
приняв i 3 .
4
1.31. По вариационному ряду производительности труда рабочих ткацкого цеха
фабрики вычислить коэффициент вариации V S , приняв i 1 .
Производительность
труда (М/час)
Число рабочих
1.32.
78,5+i 79,5+i
3+2i
79,5+i 80,5+i
9+2i
80,5+i 81,5+i
13+i
81,5+i 82,5+i
11
82,5+i 83,5+i
4
По данным задачи 1.31. вычислить моду ( Mo ), приняв i 2 .
1.33. По данным задачи 1.31. вычислить центральный момент третьего порядка ( 3 ),
приняв i 2 .
1.34. По данным задачи 1.31. вычислить коэффициент асимметрии ( Ac ), приняв
i 0.
1.35. По данным задачи 1.31. вычислить медиану ( Me ), приняв i 0 .
1.36. По данным задачи 1.31. вычислить дисперсию, приняв i 3 .
1.37. На основании ряда распределения средней урожайности пшеницы в колхозах
области вычислить коэффициент вариации V S , приняв i 1 .
Урожайность
(ц/га)
Число колхозов
1.38.
32,5+i 33,5+i
2+i
33,5+i 34,5+i
7+2i
34,5+i 35,5+i
18+i
35,5+i 36,5+i
11
36,5+i 37,5+i
2+i
По данным задачи 1.37. вычислить моду ( Mo ), приняв i 0 .
1.39. По данным задачи 1.37. вычислить центральный момент третьего порядка ( 3 ),
приняв i 2 .
1.40. По данным задачи 1.37. вычислить коэффициент асимметрии ( Ac ), приняв
i 0.
1.41. По данным задачи 1.37. вычислить медиану ( Me ), приняв i 2 .
1.42. По данным задачи 1.37. вычислить дисперсию, приняв i 3 .
5
2. РАСЧЕТ ТЕОРЕТИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ ПО
ОПЫТНЫМ ДАННЫМ.
2.2. Задачи.
2.1. По результатам выборочных наблюдений за производительностью
n 100 рабочих цеха установлено x 80 5i изд/час и S 4 i изд/час. Предполагая,
что производительность труда распределена по нормальному закону с помощью
интегральной функции Лапласа, определить при
число рабочих
i 0
производительность труда которых находится в интервале ( x 3; x 1) изд/час.
2.2.
Решить задачу 2.1. при i 1 .
2.3.
Решить задачу 2.1. при i 2 .
2.4. По результатам анализа технологического процесса получены следующие
данные:
Число дефектных
изделий в партии
Число партий
0
1
2
3
4
106+30i
63+10i
24+5i
5+4i
2+i
Используя результаты анализа и предполагая, что распределение числа дефектных
изделий в партии подчиняется закону Пуассона, определить теоретическое число
партий с m 2 дефектными изделиями, приняв i 0 .
2.5.
Решить задачу 2.4. при i 1 .
2.6.
Решить задачу 2.4. при i 2 .
2.7. По данным выборочных наблюдений установлено, что средняя скорость n 100
автомобилей равна x 80 10i км/час и S 4 2i км/час. В предположении о
нормальном распределении определить число автомобилей, скорость которых не
превышает ( x 2 ) км/час, приняв i 0 .
2.8.
Решить задачу 2.7. при i 1 .
2.9.
Решить задачу 2.7. при i 2 .
2.10. Решить задачу 2.7. при i 3 .
2.11. В результате анализа технологического процесса получен вариационный ряд
числа дефектных изделий:
Число дефектных
изделий в партии
Число партий
0
1
2
3
4
149+5i
95+5i
37+5i
13+5i
6
6
Используя результаты анализа и предполагая, что распределение числа дефектных
изделий в партии подчиняется закону Пуассона, определить теоретическое число
партий с m 3 i дефектными изделиями, приняв i 0 .
2.12. Решить задачу 2.11. при i 1 .
2.13. Решить задачу 2.11. при i 2 .
2.14. По данным наблюдений за скоростью
средняя скорость равна x 80 5i км/час и
нормальном распределении определить число
находится в интервале от x 5 км/час до x 3
n 100 автомобилей установлено, что
S 5 i км/час. В предположении о
автомобилей, скорость которых будет
км/час, приняв i 0 .
2.15. Решить задачу 2.14. при i 1 .
2.16. Решить задачу 2.14. при i 2 .
2.17. По результатам статистического приемочного контроля получен вариационный
ряд:
Число дефектных
изделий в партии
Число партий
0
1
2
3
4
5
159+5i
71+5i
35+5i
23+4i
9+i
3
Используя результаты анализа и предполагая, что число дефектных изделий в партии
распределено по закону Пуассона, определить теоретическое число партий с m 2 i
дефектными изделиями, приняв i 0 .
2.18. Решить задачу 2.17. при i 1 .
2.19. Решить задачу 2.17. при i 1 .
2.20. Обследование оплаты труда n 300 колхозников дало следующие результаты
x 320 10i рублей и S 15 2i рублей. В предположении о нормальной генеральной
совокупности определить число колхозников, оплата труда которых находится в
интервале от x 10 рублей до x 10 рублей, приняв i 0 .
2.21. Решить задачу 2.20. при i 1 .
2.22. Решить задачу 2.20. при i 2 .
2.23. По результатам статистического контроля получен вариационный ряд числа
партий из N 10 деталей по числу дефектных в них:
Число дефектных
изделий в партии из
N деталей
Число партий
0
1
2
3
4
55+2i
97+i
32+3i
5+3i
1+i
Используя результаты анализа и предполагая, что число дефектных изделий в партии
распределено по биномиальному закону, определить вероятность появления среди
n 4 i случайно отобранных изделий m 3 дефектных, приняв i 0 .
7
2.24. Решить задачу 2.23. при i 1 .
2.25. Решить задачу 2.23. при i 2 .
2.26. Решить задачу 2.23. при N 20 и i 0 .
2.27. Решить задачу 2.23. при N 20 и i 1 .
2.28. Решить задачу 2.23. при N 20 и i 2 .
2.29. В процессе контроля качества корпусов трубопроводных вентелей установлено,
что средняя длина резьбы n 200 корпусов равна x 25 5i мм и S 1 0,5i мм. В
предположении о нормальном распределении определить число корпусов, длина
резьбы которых не превысит x 0,5 мм, приняв i 0 .
2.30. Решить задачу 2.29. при i 1 .
2.31. Решить задачу 2.29. при i 2 .
2.32. В результате анализа технологического процесса получен вариационный ряд:
Число дефектных
изделий
Число партий
0
1
2
3
4
73+3i
49+3i
18+2i
9+i
1+i
Используя результаты анализа и предполагая, что число дефектных изделий в партии
распределено по закону Пуассона, определить число партий с m 1 i дефектными
изделиями, приняв i 0 .
2.33. Решить задачу 2.32. при i 1 .
2.34. Решить задачу 2.32. при i 2 .
2.35. В процессе контроля качества корпусов трубопроводных вентелей установлено,
что средняя длина резьбы n 200 корпусов равна x 25 10i мм и S 0,5 0,5i мм. В
предположении о нормальном распределении определить число корпусов, длина
резьбы которых находится в интервале от x 1 до x , приняв i 0 .
2.36. Решить задачу 2.35. при i 1 .
2.37. Решить задачу 2.35. при i 2 .
2.38. По результатам статистического контроля получен вариационный ряд числа
партий из N 10 деталей по числу дефектных в них:
Число дефектных
изделий в партии из
N деталей
Число партий
0
1
2
3
4
4+3i
62+3i
70+2i
32+i
22+i
8
Используя результаты анализа и предполагая, что число дефектных изделий в партии
распределено по биномиальному закону, определить вероятность появления среди
n 4 i случайно отобранных изделий m i 1 дефектных, приняв i 0 .
2.39. Решить задачу 2.38. при i 1 .
2.40. Решить задачу 2.38. при i 2 .
2.41. Решить задачу 2.38. при N 20 и i 0 .
2.42. Решить задачу 2.38. при N 20 и i 1 .
2.43. Решить задачу 2.383. при N 20 и i 2 .
2.44. Во время контрольных завесов пачек чая на фабрике установлено, что средний
вес у n 200 пачек чая равен x 25 10i мм и S 0,5 0,5i мм. В предположении о
нормальном распределении определить число пачек, вес которых находится в
интервале от x 1 до x 1 , приняв i 0 .
2.45. Решить задачу 2.44. при i 1 .
2.46. Решить задачу 2.44. при i 2 .
2.47. В результате анализа технологического процесса построен вариационный ряд:
Число дефектных
изделий
Число партий
0
1
2
3
80+5i
92+10i
25+3i
3+2i
Используя результаты анализа и предполагая, что число дефектных изделий в партии
подчиняется закону Пуассона, определить число партий с m 1 i дефектными
изделиями, приняв i 0 .
2.48. Решить задачу 2.47. при i 1 .
2.49. Решить задачу 2.47. при i 2 .
2.50. Во время контрольных завесов пачек чая на фабрике установлено, что средний
вес у n 300 пачек чая равен x 25 i мм и S 0,5 0,5i мм. В предположении о
нормальном распределении определить число пачек, вес которых находится в
интервале от x 1 до x 1 , приняв i 3 .
2.51. Решить задачу 2.50. при i 1 .
2.52. Решить задачу 2.50. при i 2 .
9
3. СТАТИСТИЧЕСКАЯ ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
3.2. Задачи.
3.1. По данным пяти независимых измерений одним прибором давления в паровом
котле получены следующие результаты: 24,8 23,7 24,1 24,9 24,5 атм. В
предположении о нормальном распределении определить несмещенную оценку
дисперсии.
3.2. По данным пяти независимых измерений одним прибором давления в паровом
котле получены следующие результаты: 24,4 23,5 23,7 24,3 24,1 атм. В
предположении о нормальном распределении определить несмещенную оценку
среднего квдратического отклонения.
3.3. По данным пяти независимых измерений одним прибором давления в паровом
котле получены следующие результаты: 25,4 24 24,7 25,8 25,1 атм. В предположении
о нормальном распределении определить несмещенную оценку дисперсии.
3.4. В результате измерения длины стержня прибором без систематической ошибки
получены следующие результаты: 109 113 102 121 105 мм. Найти несмещенную
оценку дисперсии ошибок прибора.
3.5. В результате измерения длины стержня прибором без систематической ошибки
получены следующие результаты: 94 103 92 106 105 мм. Найти несмещенную оценку
среднего квдратического отклонения генеральной совокупности.
3.6. В результате четырех измерений температуры печи прибором без
систематической ошибки получены данные: 809 816 810 805 0С. Определить
несмещенную оценку среднего квдратического отклонения.
3.7. В результате четырех измерений температуры печи
систематической ошибки получены данные: 807 813 809 803
несмещенную оценку дисперсии.
3.8. В результате четырех измерений температуры печи
систематической ошибки получены данные: 805 810 808 801
несмещенную оценку дисперсии генеральной совокупности,
температура в печи (генеральная средняя) равна 807 0С.
прибором без
С. Определить
0
прибором без
С. Определить
если истинная
0
3.9. По выборке объемом n = 10 получена смещенная оценка дисперсии генеральной
совокупности S 2 5 . Определить несмещенную оценку дисперсии.
3.10. По выборке объемом n = 12 получена смещенная оценка дисперсии генеральной
совокупности S 2 7 . Определить несмещенную оценку дисперсии.
3.11. По выборке объемом n = 14 получена смещенная оценка дисперсии генеральной
совокупности S 2 9 . Определить несмещенную оценку дисперсии.
3.12. На изготовление каждого из пяти электродвигателей затрачивалось
соответственно: 38 30 36 35 31 сек. Определить несмещенную оценку дисперсии
времени изготовления электродвигателя.
10
3.13. На изготовление каждого из пяти электродвигателей затрачивалось
соответственно: 38 30 40 37 35 сек. Определить несмещенную оценку среднего
квдратического отклонения времени изготовления электродвигателя.
3.14. По выборке объемом n = 10 получена смещенная оценка дисперсии генеральной
совокупности S 2 3 . Определить несмещенную оценку дисперсии.
3.15. На контрольных испытаниях n = 16 ламп было определено x 3000 ч. Считая,
что срок службы ламп распределен нормально с 20 ч., определить ширину
доверительного интервала для генеральной средней с надежностью 0,97.
3.16. На контрольных испытаниях n = 15 ламп было определено x 3000 ч. Считая,
что срок службы ламп распределен нормально с 19 ч., определить ширину
доверительного интервала для генеральной средней с надежностью 0,96.
3.17. На контрольных испытаниях n = 17 ламп было определено x 3000 ч. Считая,
что срок службы ламп распределен нормально с 21 ч., определить ширину
доверительного интервала для генеральной средней с надежностью 0,98.
3.18. По выборке объемом n = 9 вычислена выборочная средняя диаметров
поршневых колец. В предположении о нормальном распределении определить с
надежностью 0,92 точность , с которой выборочная средняя оценивает
математическое ожидание, зная что среднее квадратическое отклонение диаметров
поршневых колец равно 2.
3.19. По выборке объемом n = 16 вычислена выборочная средняя диаметров
поршневых колец. В предположении о нормальном распределении определить с
надежностью 0,94 точность , с которой выборочная средняя оценивает
математическое ожидание, зная что среднее квадратическое отклонение диаметров
поршневых колец равно 3.
3.20. По выборке объемом n = 25 вычислена выборочная средняя диаметров
поршневых колец. В предположении о нормальном распределении определить с
надежностью 0,975 точность , с которой выборочная средняя оценивает
математическое ожидание, зная что среднее квадратическое отклонение диаметров
поршневых колец равно 4.
3.21. Найти минимальный объем выборки, при котором с надежностью 0,98
точность оценки математического ожидания генеральной совокупности по выборочной
средней будет равна 0,25, если известно, что среднее квадратическое отклонение
нормальной генеральной совокупности равно 1,5.
3.22. Найти минимальный объем выборки, при котором с надежностью 0,96
точность оценки математического ожидания генеральной совокупности по выборочной
средней будет равна 0,3, если известно, что среднее квадратическое отклонение
нормальной генеральной совокупности равно 2.
3.23. Найти минимальный объем выборки, при котором с надежностью 0,87
точность оценки математического ожидания генеральной совокупности по выборочной
11
средней будет равна 0,35, если известно, что среднее квадратическое отклонение
нормальной генеральной совокупности равно 2,5.
3.24. Найти минимальный объем выборки, при котором с надежностью 0,82
точность оценки математического ожидания генеральной совокупности по выборочной
средней будет равна 0,4, если известно, что среднее квадратическое отклонение
нормальной генеральной совокупности равно 3.
3.25. Найти минимальный объем выборки, при котором с надежностью 0,75
точность оценки математического ожидания генеральной совокупности по выборочной
средней будет равна 0,45, если известно, что среднее квадратическое отклонение
нормальной генеральной совокупности равно 3,5.
3.26. В предположении о нормальной генеральной совокупности с 3 сек.,
определить минимальный объем испытаний, который нужно провести, чтобы с
надежностью 0,9 точность оценки генеральной средней времени обработки детали
составляла 1 сек.
3.27. В предположении о нормальной генеральной совокупности с 4 сек.,
определить минимальный объем испытаний, который нужно провести, чтобы с
надежностью 0,93 точность оценки генеральной средней времени обработки детали
составляла 1,5 сек.
3.28. В предположении о нормальной генеральной совокупности с 5 сек.,
определить минимальный объем испытаний, который нужно провести, чтобы с
надежностью 0,96 точность оценки генеральной средней времени обработки детали
составляла 2 сек.
3.29. На основании n = 9 испытаний установлено, что в среднем длина детали
составляет 22 мм. Допустив, что длина детали есть нормальная случайная величина с
2 мм., определить с надежностью 0,96 наибольшую длину отдельной детали.
3.30. На основании n = 10 испытаний установлено, что в среднем длина детали
составляет 24 мм. Допустив, что длина детали есть нормальная случайная величина с
3 мм., определить с надежностью 0,97 наибольшую длину отдельной детали.
3.31. На основании n = 11 испытаний установлено, что в среднем длина детали
составляет 26 мм. Допустив, что длина детали есть нормальная случайная величина с
4 мм., определить с надежностью 0,99 наибольшую длину отдельной детали.
3.32. Ошибка высотомера распределена нормально со средним квадратическим
отклонением 10 м. Сколько необходимо таких приборов на самолете, чтобы с
доверительной вероятностью 0,99 ошибка средней высоты не превышала 20 м.
Предполагается, что ошибка высотомера не имеет систематической погрешности.
3.33. Среднее значение дальности, полученное по n =4 независимым испытаниям
равно x 2300 м. Среднее квадратическое отклонение измерительного прибора 50
м. В предположении о нормальном распределении и определить доверительную
вероятность того, что точность оценивания составит 30 м.
12
3.34. Среднее значение дальности, полученное по n =16 независимым испытаниям
равно x 2300 м. Среднее квадратическое отклонение измерительного прибора 52
м. В предположении о нормальном распределении и определить доверительную
вероятность того, что точность оценивания составит 24 м.
3.35. Среднее значение дальности, полученное по n =9 независимым испытаниям
равно x 2300 м. Среднее квадратическое отклонение измерительного прибора 51
м. В предположении о нормальном распределении и определить доверительную
вероятность того, что точность оценивания составит 27 м.
3.36. Средняя продолжительность горения лампы в выборке из n =16 ламп оказалась
равной x 800 часов. В предположении о нормальном распределении с надежностью
0,95 найти верхнюю границу доверительного интервала для средней
продолжительности горения ламп всей партии, если среднее квадратическое
отклонение продолжительности горения составляет 30.
3.37. Средняя продолжительность горения лампы в выборке из n =15 ламп оказалась
равной x 810 часов. В предположении о нормальном распределении с надежностью
0,85 найти верхнюю границу доверительного интервала для средней
продолжительности горения ламп всей партии, если среднее квадратическое
отклонение продолжительности горения составляет 31.
3.38. Средняя продолжительность горения лампы в выборке из n =14 ламп оказалась
равной x 820 часов. В предположении о нормальном распределении с надежностью
0,98 найти верхнюю границу доверительного интервала для средней
продолжительности горения ламп всей партии, если среднее квадратическое
отклонение продолжительности горения составляет 32.
3.39. По результатам n = 5 измерений средняя высота детали составляет x 35 мм., а
S = 0,8 мм. В предположении о нормальном распределении определить вероятность
того, что генеральная средняя будет находиться в интервале: (34,3; 35,7).
3.40. По результатам n = 7 измерений средняя высота детали составляет x 40 мм., а
S = 1,8 мм. В предположении о нормальном распределении определить вероятность
того, что генеральная средняя будет находиться в интервале: (39,2; 40,8).
3.41. По результатам n = 9 измерений средняя высота детали составляет x 45 мм., а
S = 2,8 мм. В предположении о нормальном распределении определить вероятность
того, что генеральная средняя будет находиться в интервале: (44,1; 45,9).
3.42. По результатам n = 11 измерений средняя высота детали составляет x 50 мм., а
S = 3,8 мм. В предположении о нормальном распределении определить вероятность
того, что генеральная средняя будет находиться в интервале: (49; 51).
3.43. По данным контрольных испытаний n = 10 ламп определены оценки x 1600 ч.
и S = 19 ч. Считая, что срок службы ламп распределен нормально, определить с какой
вероятностью можно утверждать, что ошибка в определении генеральной средней не
превышает 12 ч.
3.44. По данным контрольных испытаний n = 8 ламп определены оценки x 1600 ч. и
S = 17 ч. Считая, что срок службы ламп распределен нормально, определить с какой
13
вероятностью можно утверждать, что ошибка в определении генеральной средней не
превышает 11 ч.
3.45. По данным контрольных испытаний n = 12 ламп определены оценки x 1600 ч.
и S = 21 ч. Считая, что срок службы ламп распределен нормально, определить с какой
вероятностью можно утверждать, что ошибка в определении генеральной средней не
превышает 13 ч.
3.46. По данным контрольных испытаний n = 14 ламп определены оценки x 1600 ч.
и S = 23 ч. Считая, что срок службы ламп распределен нормально, определить с какой
вероятностью можно утверждать, что ошибка в определении генеральной средней не
превышает 14 ч.
3.47. На основании измерения n = 11 деталей вычислена выборочная средняя и S = 10
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,95 точность оценки генеральной средней.
3.48. На основании измерения n = 7 деталей вычислена выборочная средняя и S = 8
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,98 точность оценки генеральной средней.
3.49. На основании измерения n = 9 деталей вычислена выборочная средняя и S = 9
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,7 точность оценки генеральной средней.
3.50. На основании измерения n = 13 деталей вычислена выборочная средняя и S = 11
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,999 точность оценки генеральной средней.
3.51. На основании n = 9 измерений температуры одним прибором определена
выборочная средняя x 6000С и S = 100С. Предполагая, что погрешность измерения
есть нормальная случайная величина, определить вероятность того, что абсолютная
величина ошибки в оценке истинной температуры не превысит 140С.
3.52. На основании n = 4 измерений температуры одним прибором определена
выборочная средняя x 4000С и S = 90С. Предполагая, что погрешность измерения есть
нормальная случайная величина, определить вероятность того, что абсолютная
величина ошибки в оценке истинной температуры не превысит 130С.
3.53. На основании n = 16 измерений температуры одним прибором определена
выборочная средняя x 8000С и S = 110С. Предполагая, что погрешность измерения
есть нормальная случайная величина, определить вероятность того, что абсолютная
величина ошибки в оценке истинной температуры не превысит 150С.
3.54. На основании n = 7 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 44 сек. и S = 3 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить с надежностью
0,98 верхнюю границу для оценки среднего времени изготовления одного диода.
3.55. На основании n = 9 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 48 сек. и S = 4 сек. Предположив, что время
14
изготовления диода есть нормальная случайная величина, определить с надежностью
0,8 верхнюю границу для оценки среднего времени изготовления одного диода.
3.56. На основании n = 11 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 52 сек. и S = 5 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить с надежностью
0,95 верхнюю границу для оценки среднего времени изготовления одного диода.
3.57. На основании n = 13 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 56 сек. и S = 6 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить с надежностью
0,999 верхнюю границу для оценки среднего времени изготовления одного диода.
3.58. Для определения максимальной скорости самолета было проведено n = 5
испытаний, в результате которых были вычислены x 800 м/сек. и S = 10 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, найти
вероятность того, что доверительный интервал для оценки генеральной средней равен
(792; 808).
3.59. Для определения максимальной скорости самолета было проведено n = 7
испытаний, в результате которых были вычислены x 700 м/сек. и S = 12 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, найти
вероятность того, что доверительный интервал для оценки генеральной средней равен
(693; 707).
3.60. Для определения максимальной скорости самолета было проведено n = 9
испытаний, в результате которых были вычислены x 600 м/сек. и S = 14 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, найти
вероятность того, что доверительный интервал для оценки генеральной средней равен
(594; 606).
3.61. Для определения максимальной скорости самолета было проведено n = 11
испытаний, в результате которых были вычислены x 500 м/сек. и S = 16 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, найти
вероятность того, что доверительный интервал для оценки генеральной средней равен
(495; 505).
3.62. На основании измерения диаметров n = 8 поршневых колец найдены
выборочная средняя и S = 20 мк. Найти с надежностью 0,95 точность, с которой
выборочная средняя оценивает генеральную среднюю. Предполагается, что ошибка
измерения распределена нормально.
3.63. На основании измерения диаметров n = 9 поршневых колец найдены
выборочная средняя и S = 23 мк. Найти с надежностью 0,98 точность, с которой
выборочная средняя оценивает генеральную среднюю. Предполагается, что ошибка
измерения распределена нормально.
3.64. На основании измерения диаметров n = 11 поршневых колец найдены
выборочная средняя и S = 29 мк. Найти с надежностью 0,99 точность, с которой
выборочная средняя оценивает генеральную среднюю. Предполагается, что ошибка
измерения распределена нормально.
15
3.65. На основании измерения диаметров n = 10 поршневых колец найдены
выборочная средняя и S = 26 мк. Найти с надежностью 0,9 точность, с которой
выборочная средняя оценивает генеральную среднюю. Предполагается, что ошибка
измерения распределена нормально.
3.66. По данным контрольных испытаний n = 5 ламп были получены оценки x 300
ч. и S = 20 ч. Считая, что срок службы ламп распределен нормально, определить
нижнюю границу доверительного интервала для генеральной средней с надежностью
0,9.
3.67. По данным контрольных испытаний n = 7 ламп были получены оценки x 330
ч. и S = 23 ч. Считая, что срок службы ламп распределен нормально, определить
нижнюю границу доверительного интервала для генеральной средней с надежностью
0,8.
3.68. По данным контрольных испытаний n = 11 ламп были получены оценки x 390
ч. и S = 29 ч. Считая, что срок службы ламп распределен нормально, определить
нижнюю границу доверительного интервала для генеральной средней с надежностью
0,99.
3.69. По данным контрольных испытаний n = 9 ламп были получены оценки x 360
ч. и S = 26 ч. Считая, что срок службы ламп распределен нормально, определить
нижнюю границу доверительного интервала для генеральной средней с надежностью
0,95.
3.70. По результатам n = 5 измерений средняя высота детали составляет x 35 мм., а
S = 0,8 мм. В предположении о нормальном распределении определить вероятность
того, что абсолютная величина ошибки определения среднего квадратического
отклонения не превысит 0,1 мм.
3.71. По результатам n = 7 измерений средняя высота детали составляет x 40 мм., а
S = 1,8 мм. В предположении о нормальном распределении определить с надежностью
0,98 верхнюю границу доверительного интервала для дисперсии 2 .
3.72. По результатам n = 9 измерений средняя высота детали составляет x 45 мм., а
S = 2,8 мм. В предположении о нормальном распределении определить вероятность
того, что абсолютная величина ошибки определения среднего квадратического
отклонения не превысит 8% от S.
3.73. По данным контрольных испытаний n = 10 ламп определены оценки x 1600 ч.
и S = 19 ч. Считая, что срок службы ламп распределен нормально, определить с
надежностью 0,99 верхнюю границу доверительного интервала для дисперсии 2 .
3.74. По данным контрольных испытаний n = 8 ламп определены оценки x 1600 ч. и
S = 17 ч. Считая, что срок службы ламп распределен нормально, определить
вероятность того, что абсолютная величина ошибки определения среднего
квадратического отклонения не превысит 10% от S.
3.75. По данным контрольных испытаний n = 12 ламп определены оценки x 1600 ч.
и S = 21 ч. Считая, что срок службы ламп распределен нормально, определить с
надежностью 0,95 максимально возможное значение дисперсии 2 .
16
3.76. По данным контрольных испытаний n = 14 ламп определены оценки x 1600 ч.
и S = 23 ч. Считая, что срок службы ламп распределен нормально, определить с
надежностью 0,98 нижнюю границу доверительного интервала для дисперсии 2 .
3.77. На основании измерения n = 11 деталей вычислена выборочная средняя и S = 10
мк. Предполагая, что ошибка изготовления распределена нормально, определить
вероятность того, что абсолютная величина ошибки определения среднего
квадратического отклонения не превысит 9% от S.
3.78. На основании измерения n = 7 деталей вычислена выборочная средняя и S = 8
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,9 максимально возможное значение дисперсии ошибки измерения
2.
3.79. На основании измерения n = 9 деталей вычислена выборочная средняя и S = 9
мк. Предполагая, что ошибка изготовления распределена нормально, определить с
надежностью 0,99 нижнюю границу доверительного интервала для дисперсии 2 .
3.80. На основании измерения n = 13 деталей вычислена выборочная средняя и S = 11
мк. Предполагая, что ошибка изготовления распределена нормально, определить
вероятность того, что истинное значение среднего квадратического отклонения будет
находится в интервале (0,89S; 1,11S).
3.81. На основании n = 9 измерений температуры одним прибором определена
выборочная средняя x 6000С и S = 100С. Предполагая, что погрешность измерения
есть нормальная случайная величина, определить с надежностью 0,9 максимально
возможное значение дисперсии ошибки измерения 2 .
3.82. На основании n = 4 измерений температуры одним прибором определена
выборочная средняя x 4000С и S = 90С. Предполагая, что погрешность измерения есть
нормальная случайная величина, определить с надежностью 0,9 нижнюю границу
доверительного интервала для дисперсии 2 .
3.83. На основании n = 16 измерений температуры одним прибором определена
выборочная средняя x 8000С и S = 110С. Предполагая, что погрешность измерения ,
определить вероятность того, что истинное значение среднего квадратического
отклонения будет находится в интервале (0,95S; 1,05S).
3.84. На основании n = 7 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 44 сек. и S = 3 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить с надежностью
0,95 нижнюю границу доверительного интервала для дисперсии 2 .
3.85. На основании n = 9 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 48 сек. и S = 4 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить вероятность того,
что истинное значение среднего квадратического отклонения времени изготовления
диода будет находится в интервале (0,92S; 1,08S).
17
3.86. На основании n = 11 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 52 сек. и S = 5 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить с надежностью
0,98 ширину доверительного интервала для оценки дисперсии времени
изготовления диода.
3.87. На основании n = 13 испытаний установлено, что в среднем для изготовления
полупроводникового диода требуется x 56 сек. и S = 6 сек. Предположив, что время
изготовления диода есть нормальная случайная величина, определить вероятность того,
что истинное значение дисперсии времени изготовления диода будет находится в
интервале (0,9S2; 1,1S2).
3.88. Для определения максимальной скорости самолета было проведено n = 5
испытаний, в результате которых были вычислены x 800 м/сек. и S = 10 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, определить
вероятность того, что истинное значение среднего квадратического отклонения будет
находится в интервале (0,98S; 1,02S).
3.89. Для определения максимальной скорости самолета было проведено n = 7
испытаний, в результате которых были вычислены x 700 м/сек. и S = 12 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, определить с
надежностью 0,9 ширину доверительного интервала для оценки дисперсии
генеральной совокупности.
3.90. Для определения максимальной скорости самолета было проведено n = 9
испытаний, в результате которых были вычислены x 600 м/сек. и S = 14 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, определить
вероятность того, что истинное значение дисперсии генеральной совокупности будет
находится в интервале (0,85S2; 1,15S2).
3.91. Для определения максимальной скорости самолета было проведено n = 11
испытаний, в результате которых были вычислены x 500 м/сек. и S = 16 м/сек.
Предполагая, что рассеяние скорости подчинено нормальному закону, определить
вероятность того, что абсолютная величина ошибки определения среднего
квадратического отклонения не превысит 0,5 м/сек.
3.92. На основании измерения диаметров n = 8 поршневых колец найдены
выборочная средняя и
S = 20 мк. Найти с надежностью 0,99 ширину
доверительного интервала для оценки дисперсии генеральной совокупности.
Предполагается, что ошибка измерения распределена нормально.
3.93. На основании измерения диаметров n = 9 поршневых колец найдены
выборочная средняя и S = 23 мк. Определить вероятность того, что истинное значение
дисперсии генеральной совокупности будет находится в интервале (0,9S2; 1,1S2).
Предполагается, что ошибка измерения распределена нормально.
3.94. На основании измерения диаметров n = 10 поршневых колец найдены
выборочная средняя и S = 26 мк. Определить вероятность того, что абсолютная
величина ошибки определения среднего квадратического отклонения не превысит
1,5 мк. Предполагается, что ошибка измерения распределена нормально.
18
3.95. На основании измерения диаметров n = 11 поршневых колец найдены
выборочная средняя и S = 29 мк. Определить с надежностью 0,95 верхнюю границу
доверительного интервала для дисперсии 2 . Предполагается, что ошибка измерения
распределена нормально.
3.96. По данным контрольных испытаний n = 5 ламп были получены оценки x 300
ч. и S = 20 ч. Считая, что срок службы ламп распределен нормально, определить
вероятность того, что истинное значение дисперсии генеральной совокупности будет
находится в интервале (0,97S2; 1,03S2).
3.97. По данным контрольных испытаний n = 7 ламп были получены оценки x 330
ч. и S = 23 ч. Считая, что срок службы ламп распределен нормально, определить
вероятность того, что абсолютная величина ошибки определения среднего
квадратического отклонения не превысит 4 ч.
3.98. По данным контрольных испытаний n = 9 ламп были получены оценки x 360
ч. и S = 26 ч. Считая, что срок службы ламп распределен нормально, определить с
надежностью 0,98 верхнюю границу доверительного интервала для дисперсии 2 .
3.99. По данным контрольных испытаний n = 11 ламп были получены оценки x 390
ч. и S = 29 ч. Считая, что срок службы ламп распределен нормально, определить
вероятность того, что абсолютная величина ошибки определения среднего
квадратического отклонения не превысит 10% от S.
3.100. Из 100 отобранных деталей m = 40 оказалось второго сорта. В предположении о
биномиальном распределении определить доверительную вероятность того, что
точность оценки вероятности появления детали второго сорта будет равна 0,04.
3.101. Из 100 отобранных деталей m = 50 оказалось второго сорта. В предположении о
биномиальном распределении определить доверительную вероятность того, что
точность оценки вероятности появления детали второго сорта будет равна 0,05.
3.102. Из 100 отобранных деталей m = 60 оказалось второго сорта. В предположении о
биномиальном распределении определить доверительную вероятность того, что
точность оценки вероятности появления детали второго сорта будет равна 0,06.
3.103. Из 400 клубней картофеля, поступивших на контроль, вес m = 100 превысил 50
г. В предположении о биномиальном распределении определить с надежностью
0,98 верхнюю границу доверительного интервала для вероятности того, что вес
клубня превысит 50 г.
3.104. Из 400 клубней картофеля, поступивших на контроль, вес m = 200 превысил 50
г. В предположении о биномиальном распределении определить с надежностью 0,9
верхнюю границу доверительного интервала для вероятности того, что вес клубня
превысит 50 г.
3.105. Из 400 клубней картофеля, поступивших на контроль, вес m = 300 превысил 50
г. В предположении о биномиальном распределении определить с надежностью
0,95 верхнюю границу доверительного интервала для вероятности того, что вес
клубня превысит 50 г.
19
3.106. На основании n = 81 опытов установлено, что в среднем для нарезания резьбы
требуется x 20 сек., а S = 4 сек. Определить с надежностью 0,9 верхнюю границу
доверительного интервала для оценки генеральной средней времени нарезания резьбы.
3.107. На основании n = 100 опытов установлено, что в среднем для нарезания резьбы
требуется x 30 сек., а S = 5 сек. Определить с надежностью 0,95 верхнюю границу
доверительного интервала для оценки генеральной средней времени нарезания резьбы.
3.108. На основании n = 121 опытов установлено, что в среднем для нарезания резьбы
требуется x 40 сек., а S = 6 сек. Определить с надежностью 0,98 верхнюю границу
доверительного интервала для оценки генеральной средней времени нарезания резьбы.
3.109. По результатам n = 36 измерений длины корпусов было получено x 200 мм. и
S = 3 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (199; 201).
3.110. По результатам n = 49 измерений длины корпусов было получено x 300 мм. и
S = 6 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (298; 302).
3.111. По результатам n = 64 измерений длины корпусов было получено x 400 мм. и
S = 9 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (397; 403).
3.112. Стрелок из 200 выстрелов попал в цель m = 86 раз. Определить с надежностью
0,95 верхнюю границу доверительного интервала для вероятности попадания в цель
одним выстрелом. Предполагается, что число попаданий в цель имеет биномиальное
распределение.
3.113. Стрелок из 200 выстрелов попал в цель m = 96 раз. Определить с надежностью
0,98 верхнюю границу доверительного интервала для вероятности попадания в цель
одним выстрелом. Предполагается, что число попаданий в цель имеет биномиальное
распределение.
3.114. Стрелок из 200 выстрелов попал в цель m = 106 раз. Определить с надежностью
0,9 верхнюю границу доверительного интервала для вероятности попадания в цель
одним выстрелом. Предполагается, что число попаданий в цель имеет биномиальное
распределение.
3.115. Из 250 поступивших на сортировку шариков для подшипников m = 50 попало в
первую группу. В предположении о биномиальном распределении определить
доверительную вероятность того, что вероятность попадания шарика в первую группу
будет находиться в интервале (0,15; 0,25).
3.116. Из 250 поступивших на сортировку шариков для подшипников m = 60 попало в
первую группу. В предположении о биномиальном распределении определить
доверительную вероятность того, что вероятность попадания шарика в первую группу
будет находиться в интервале (0,15; 0,25).
3.117. Из 250 поступивших на сортировку шариков для подшипников m = 70 попало в
первую группу. В предположении о биномиальном распределении определить
20
доверительную вероятность того, что вероятность попадания шарика в первую группу
будет находиться в интервале (0,15; 0,25).
3.118. По результатам n = 64 измерений длины деталей было получено x 30 мм. и S =
5 мм. Определить с надежностью 0,98 верхнюю границу доверительного интервала
для оценки генеральной средней.
3.119. По результатам n = 70 измерений длины деталей было получено x 40 мм. и S =
6 мм. Определить с надежностью 0,9 верхнюю границу доверительного интервала
для оценки генеральной средней.
3.120. По результатам n = 76 измерений длины деталей было получено x 50 мм. и S =
7 мм. Определить с надежностью 0,85 верхнюю границу доверительного интервала
для оценки генеральной средней.
3.121. По результатам n = 50 измерений диаметров валиков было получено x 150 мм.
и S = 4,1 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (149; 151).
3.122. По результатам n = 60 измерений диаметров валиков было получено x 150 мм.
и S = 4,1 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (149; 151).
3.123. По результатам n = 70 измерений диаметров валиков было получено x 150 мм.
и S = 6,1 мм. Определить вероятность того, что генеральная средняя будет находиться
внутри интервала (149; 151).
3.124. По результатам n = 50 опытов установлено, что в среднем для сборки
трансформатора требуется x 100 сек. и S = 8 сек. В предположении о нормальном
распределении определить с надежностью 0,9 верхнюю границу доверительного
интервала для оценки неизвестного параметра генеральной совокупности.
3.125. По результатам n = 50 опытов установлено, что в среднем для сборки
трансформатора требуется x 100 сек. и S = 10 сек. В предположении о нормальном
распределении определить с надежностью 0,99 верхнюю границу доверительного
интервала для оценки неизвестного параметра генеральной совокупности.
3.126. По результатам n = 50 опытов установлено, что в среднем для сборки
трансформатора требуется x 100 сек. и S = 12 сек. В предположении о нормальном
распределении определить с надежностью 0,85 верхнюю границу доверительного
интервала для оценки неизвестного параметра генеральной совокупности.
3.127. По результатам n = 50 опытов установлено, что в среднем для сборки
трансформатора требуется x 100 сек. и S = 16 сек. В предположении о нормальном
распределении определить с надежностью 0,92 верхнюю границу доверительного
интервала для оценки неизвестного параметра генеральной совокупности.
3.128. По результатам измерения диаметра n = 50 корпусов электродвигателей
получено x 100 мм. и S = 1,6 мм. В предположении о нормальном распределении
найти вероятность того, что среднее квадратическое отклонение будет находиться
внутри интервала (1,5; 1,7).
21
3.129. По результатам измерения диаметра n = 50 корпусов электродвигателей
получено x 100 мм. и S = 3,6 мм. В предположении о нормальном распределении
найти вероятность того, что среднее квадратическое отклонение будет находиться
внутри интервала (3,5; 3,7).
3.130. По результатам измерения диаметра n = 50 корпусов электродвигателей
получено x 100 мм. и S = 5,6 мм. В предположении о нормальном распределении
найти вероятность того, что среднее квадратическое отклонение будет находиться
внутри интервала (5,5; 5,7).
3.131. По результатам измерения диаметра n = 50 корпусов электродвигателей
получено x 100 мм. и S = 7,6 мм. В предположении о нормальном распределении
найти вероятность того, что среднее квадратическое отклонение будет находиться
внутри интервала (7,5; 7,7).
3.132. Случайно отобранная партия из 8 приборов была подвергнута испытаниям на
срок безотказной работы. Из них 4 прибора проработало без отказа свыше 200 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,8 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 200 часов.
3.133. Случайно отобранная партия из 4 приборов была подвергнута испытаниям на
срок безотказной работы. Из них 2 прибора проработало без отказа свыше 200 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,9 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 200 часов.
3.134. Случайно отобранная партия из 6 приборов была подвергнута испытаниям на
срок безотказной работы. Из них 3 прибора проработало без отказа свыше 200 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,99 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 200 часов.
3.135. Случайно отобранная партия из 10 приборов была подвергнута испытаниям на
срок безотказной работы. Из них 5 приборов проработало без отказа свыше 200 часов.
В предположении о биномиальном законе распределения определить с надежностью
0,95 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 200 часов.
3.136. Из случайно отобранных 6 приборов, подвергнутых испытаниям на срок
безотказной работы, 3 прибора проработало без отказа свыше 300 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,95 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 300 часов.
3.137. Из случайно отобранных 8 приборов, подвергнутых испытаниям на срок
безотказной работы, 4 прибора проработало без отказа свыше 300 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,9 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 300 часов.
22
3.138. Из случайно отобранных 4 приборов, подвергнутых испытаниям на срок
безотказной работы, 2 прибора проработало без отказа свыше 300 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,7 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 300 часов.
3.139. Из случайно отобранных 10 приборов, подвергнутых испытаниям на срок
безотказной работы, 5 приборов проработало без отказа свыше 300 часов. В
предположении о биномиальном законе распределения определить с надежностью
0,85 верхнюю границу вероятности того, что один случайно отобранный прибор
проработает свыше 300 часов.
3.140. По результатам n = 64 опытов установлено, что в среднем для сборки вентеля
требуется x 30 сек. и S = 5 сек. В предположении о нормальном распределении
определить с надежностью 0,95 верхнюю границу доверительного интервала для
оценки неизвестного параметра генеральной совокупности.
3.141. По результатам n = 81 опытов установлено, что в среднем для сборки вентеля
требуется x 30 сек. и S = 6 сек. В предположении о нормальном распределении
определить с надежностью 0,9 верхнюю границу доверительного интервала для
оценки неизвестного параметра генеральной совокупности.
3.142. По результатам n = 100 опытов установлено, что в среднем для сборки вентеля
требуется x 30 сек. и S = 7 сек. В предположении о нормальном распределении
определить с надежностью 0,98 верхнюю границу доверительного интервала для
оценки неизвестного параметра генеральной совокупности.
3.143. На основании выборочных наблюдений за производительностью труда n = 32
рабочих вычислено x 400 м/час и S = 10 м/час. В предположении о нормальном
распределении найти вероятность того, что среднее квадратическое отклонение
будет находиться внутри интервала (9; 11).
3.144. На основании выборочных наблюдений за производительностью труда n = 37
рабочих вычислено x 400 м/час и S = 12 м/час. В предположении о нормальном
распределении найти вероятность того, что среднее квадратическое отклонение
будет находиться внутри интервала (11; 13).
3.145. На основании выборочных наблюдений за производительностью труда n = 42
рабочих вычислено x 400 м/час и S = 14 м/час. В предположении о нормальном
распределении найти вероятность того, что среднее квадратическое отклонение
будет находиться внутри интервала (13; 15).
3.146. На основании выборочных наблюдений за производительностью труда n = 47
рабочих вычислено x 400 м/час и S = 16 м/час. В предположении о нормальном
распределении найти вероятность того, что среднее квадратическое отклонение
будет находиться внутри интервала (15; 17).
23
4. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
4.2. Задачи.
4.1. С помощью критерия Пирсона на уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения на основании следующих данных, приняв
i=0:
mi
3+i
15+i
11+i
7+i
4+i
T
i
4+i
9+2i
15+2i
9
3
m
4.2.
Решить задачу 4.1. при i=1 и 0,01.
4.3.
Решить задачу 4.1. при i=2 и 0,025.
4.4.
Решить задачу 4.1. при i=3 и 0,025.
4.5. С помощью критерия Пирсона на уровне значимости 0,05 проверить
гипотезу о биномиальном законе распределения на основании следующих данных,
приняв i=0:
mi
80+15i
20(5+i)
15+10i
5(1+i)
T
i
97+20i
70+15i
25+12i
8+3i
m
4.6.
Решить задачу 4.5. при i=1 и 0,02.
4.7.
Решить задачу 4.5. при i=2 и 0,001.
4.8.
Решить задачу 4.5. при i=3 и 0,005.
4.9. С помощью критерия Пирсона на уровне значимости 0,01 проверить
гипотезу о законе распределения Пуассона на основании следующих данных, приняв
i=0:
mi
10(7+i)
25(4+i)
27+12i
3(1+i)
m iT
88+12i
72+30i
30+8i
10
4.10. Решить задачу 4.9. при i=1 и 0,02.
4.11. Решить задачу 4.9. при i=2 и 0,025.
4.12. Решить задачу 4.9. при i=3 и 0,05.
4.13. С помощью критерия Пирсона на уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения на основании следующих данных, приняв
i=0:
mi
2+i
14+4i
16+3i
7+2i
4
m iT
4+i
12+3i
15+3i
24
9+2i
3+i
4.14. Решить задачу 4.13. при i=1 и 0,01.
4.15. Решить задачу 4.13. при i=2 и 0,001.
4.16. Решить задачу 4.13. при i=3 и 0,02.
4.17. С помощью критерия Пирсона на уровне значимости 0,025 проверить
гипотезу о нормальном законе распределения на основании следующих данных, приняв
i=0:
mi
5+i
10+3i
20+2i
25+3i
14+i
3
m iT
6+2i
14+3i
28+i
18+2i
8+2i
3
4.18. Решить задачу 4.17. при i=1 и 0,05.
4.19. Решить задачу 4.17. при i=2 и 0,01.
4.20. Решить задачу 4.17. при i=3 и 0,01.
4.21. С помощью критерия Пирсона на уровне значимости 0,05 проверить
гипотезу о законе распределения Пуассона на основании следующих данных, приняв
i=0:
mi
115+15i
60+15i
20+15i
5(1+i)
m iT
112+25i
65+15i
19+8i
4+2i
4.22. Решить задачу 4.21. при i=1 и 0,025.
4.23. Решить задачу 4.21. при i=2 и 0,01.
4.24. Решить задачу 4.21. при i=3 и 0,005.
4.25. С помощью критерия Пирсона на уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения на основании следующих данных, приняв
i=0:
mi
3+i
10+2i
15+3i
14+2i
6+i
2+i
m iT
3+2i
6+i
17+2i
16+3i
5+2i
3
4.26. Решить задачу 4.25. при i=1 и 0,01.
4.27. Решить задачу 4.25. при i=2 и 0,02.
4.28. Решить задачу 4.25. при i=3 и 0,005.
4.29. По результатам n = 4 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 60С.
25
Проверить на уровне значимости 0,05
альтернативной гипотезы H 1 : 2600С.
гипотезу
H 0 : 2500С
против
4.30. По результатам n = 6 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 70С.
Проверить на уровне значимости 0,02 гипотезу H 0 : 2500С против
альтернативной гипотезы H 1 : 2600С.
4.31. По результатам n = 8 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 80С.
Проверить на уровне значимости 0,01 гипотезу H 0 : 2500С против
альтернативной гипотезы H 1 : 2600С.
4.32. По результатам n = 10 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 90С.
Проверить на уровне значимости 0,08 гипотезу H 0 : 2500С против
альтернативной гипотезы H 1 : 2600С.
4.33. По результатам n = 4 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 60С.
Вычислить мощность критерия при проверке на уровне значимости 0,05 гипотезы
H 0 : 2500С против альтернативной гипотезы H 1 : 2600С.
4.34. По результатам n = 6 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 70С.
Вычислить мощность критерия при проверке на уровне значимости 0,02 гипотезы
H 0 : 2500С против альтернативной гипотезы H 1 : 2600С.
4.35. По результатам n = 8 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 80С.
Вычислить мощность критерия при проверке на уровне значимости 0,01 гипотезы
H 0 : 2500С против альтернативной гипотезы H 1 : 2600С.
4.36. По результатам n = 10 измерений температуры в печи найдено x 2540С.
Предполагается, что ошибка измерения есть нормальная случайная величина с 90С.
Вычислить мощность критерия при проверке на уровне значимости 0,08 гипотезы
H 0 : 2500С против альтернативной гипотезы H 1 : 2600С.
4.37. На контрольных испытаниях n = 16 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 20 ч. Проверить на уровне значимости
0,1 гипотезу H 0 : 300 ч. против альтернативной гипотезы H1 : 290 ч.
4.38. На контрольных испытаниях n = 14 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 22 ч. Проверить на уровне значимости
0,05 гипотезу H 0 : 300 ч. против альтернативной гипотезы H1 : 290 ч.
26
4.39. На контрольных испытаниях n = 12 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 24 ч. Проверить на уровне значимости
0,01 гипотезу H 0 : 300 ч. против альтернативной гипотезы H1 : 290 ч.
4.40. На контрольных испытаниях n = 10 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 26 ч. Проверить на уровне значимости
0,025 гипотезу H 0 : 300 ч. против альтернативной гипотезы H1 : 290 ч.
4.41. На контрольных испытаниях n = 14 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 22 ч. Проверить на уровне значимости
0,02 гипотезу H 0 : 285 ч. против альтернативной гипотезы H1 : 285 ч.
4.42. На контрольных испытаниях n = 12 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 24 ч. Проверить на уровне значимости
0,15 гипотезу H 0 : 287 ч. против альтернативной гипотезы H1 : 287 ч.
4.43. На контрольных испытаниях n = 16 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 20 ч. Проверить на уровне значимости
0,08 гипотезу H 0 : 295 ч. против альтернативной гипотезы H1 : 295 ч.
4.44. На контрольных испытаниях n = 16 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 20 ч. Вычислить мощность критерия
при проверке на уровне значимости 0,1 гипотезы H 0 : 300 ч. против
альтернативной гипотезы H 1 : 290 ч.
4.45. На контрольных испытаниях n = 14 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 22 ч. Вычислить мощность критерия
при проверке на уровне значимости 0,05 гипотезы H 0 : 300 ч. против
альтернативной гипотезы H 1 : 290 ч.
4.46. На контрольных испытаниях n = 12 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 24 ч. Вычислить мощность критерия
при проверке на уровне значимости 0,01 гипотезы H 0 : 300 ч. против
альтернативной гипотезы H 1 : 290 ч.
4.47. На контрольных испытаниях n = 10 ламп было определено x 291 ч. Считая, что
срок службы ламп распределен нормально с 26 ч. Вычислить мощность критерия
при проверке на уровне значимости 0,01 гипотезы H 0 : 300 ч. против
альтернативной гипотезы H 1 : 290 ч.
4.48. На основании n = 5 измерений найдено, что средняя высота сальниковой камеры
x 51 мм., а S 1,2 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,01 гипотезу H 0 : 50 мм. против конкурирующей гипотезы
H 1 : 53 мм.
27
4.49. На основании n = 7 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 1,7 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,05 гипотезу H 0 : 50 мм. против конкурирующей гипотезы
H 1 : 53 мм.
4.50. На основании n = 9 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 2,2 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,1 гипотезу H 0 : 50 мм. против конкурирующей гипотезы
H 1 : 53 мм.
4.51. На основании n = 11 измерений найдено, что средняя высота сальниковой
камеры x 51 мм., а S 2,7 мм. В предположении о нормальном распределении
проверить на уровне значимости 0,01 гипотезу H 0 : 50 мм. против
конкурирующей гипотезы H 1 : 53 мм.
4.52. На основании n = 5 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 1,2 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,01 гипотезу H 0 : 49,5 мм. против конкурирующей
гипотезы H 1 : 49,5 мм.
4.53. На основании n = 7 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 1,7 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,05 гипотезу H 0 : 49 мм. против конкурирующей гипотезы
H 1 : 49 мм.
4.54. На основании n = 9 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 2,2 мм. В предположении о нормальном распределении проверить на
уровне значимости 0,02 гипотезу H 0 : 52 мм. против конкурирующей гипотезы
H 1 : 52 мм.
4.55. На основании n = 5 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 1,2 мм. В предположении о нормальном распределении вычислить
мощность критерия при проверке на уровне значимости 0,01 гипотезы H 0 : 50
мм. против конкурирующей гипотезы H 1 : 53 мм.
4.56. На основании n = 7 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 1,7 мм. В предположении о нормальном распределении вычислить
мощность критерия при проверке на уровне значимости 0,05 гипотезы H 0 : 50
мм. против конкурирующей гипотезы H 1 : 53 мм.
4.57. На основании n = 9 измерений найдено, что средняя высота сальниковой камеры
x 51 мм, а S 2,2 мм. В предположении о нормальном распределении вычислить
мощность критерия при проверке на уровне значимости 0,1 гипотезы H 0 : 50
мм. против конкурирующей гипотезы H 1 : 53 мм.
4.58. На основании n = 11 измерений найдено, что средняя высота сальниковой
камеры x 51 мм., а S 2,7 мм. В предположении о нормальном распределении
28
вычислить мощность критерия при проверке на уровне значимости 0,01 гипотезы
H 0 : 50 мм. против конкурирующей гипотезы H 1 : 53 мм.
4.59. На основании контроля n = 10 деталей найдено, что x 104 мм., а S 5 мм. В
предположении о нормальном распределении проверить на уровне значимости 0,01
гипотезу H 0 : 110 мм. против конкурирующей гипотезы H 1 : 100 мм.
4.60. На основании контроля n = 12 деталей найдено, что x 104 мм., а S 6 мм. В
предположении о нормальном распределении проверить на уровне значимости 0,05
гипотезу H 0 : 110 мм. против конкурирующей гипотезы H 1 : 100 мм.
4.61. На основании контроля n = 14 деталей найдено, что x 104 мм., а S 7 мм. В
предположении о нормальном распределении проверить на уровне значимости 0,1
гипотезу H 0 : 110 мм. против конкурирующей гипотезы H 1 : 100 мм.
4.62. На основании контроля n = 16 деталей найдено, что x 104 мм., а S 8 мм. В
предположении о нормальном распределении проверить на уровне значимости
0,005 гипотезу H 0 : 110 мм. против конкурирующей гипотезы H1 : 100 мм.
4.63. На основании контроля n = 10 деталей найдено, что x 104 мм., а S 5 мм. В
предположении о нормальном распределении вычислить мощность критерия при
проверке на уровне значимости 0,01 гипотезы H 0 : 110 мм. против
конкурирующей гипотезы H 1 : 100 мм.
4.64. На основании контроля n = 12 деталей найдено, что x 104 мм., а S 6 мм. В
предположении о нормальном распределении вычислить мощность критерия при
проверке на уровне значимости 0,05 гипотезы H 0 : 110 мм. против
конкурирующей гипотезы H 1 : 100 мм.
4.65. На основании контроля n = 14 деталей найдено, что x 104 мм., а S 7 мм. В
предположении о нормальном распределении вычислить мощность критерия при
проверке на уровне значимости 0,1 гипотезы H 0 : 110 мм. против
конкурирующей гипотезы H 1 : 100 мм.
4.66. На основании контроля n = 16 деталей найдено, что x 104 мм., а S 8 мм. В
предположении о нормальном распределении вычислить мощность критерия при
проверке на уровне значимости 0,005 гипотезы H 0 : 110 мм. против
конкурирующей гипотезы H 1 : 100 мм.
4.67. На основании контроля n = 6 измерений найдено, что x 70 мм., а S 1,5мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
уровне значимости 0,01 гипотезу H 0 : 2 3,25 мм2. против конкурирующей
гипотезы H 1 : 2 1,25 мм2.
4.68. На основании контроля n = 9 измерений найдено, что x 70 мм., а S 2 мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
29
уровне значимости 0,05 гипотезу H 0 : 2 5 мм2. против конкурирующей гипотезы
H 1 : 2 3 мм2.
4.69. На основании контроля n = 12 измерений найдено, что x 70 мм., а S 2,5мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
уровне значимости 0,1 гипотезу H 0 : 2 7,25 мм2. против конкурирующей
гипотезы H 1 : 2 5,25 мм2.
4.70. На основании контроля n = 15 измерений найдено, что x 70 мм., а S 3 мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
уровне значимости 0,02 гипотезу H 0 : 2 10 мм2. против конкурирующей
гипотезы H 1 : 2 8 мм2..
4.71. На основании контроля n = 9 измерений найдено, что x 70 мм., а S 2 мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
уровне значимости 0,1 гипотезу H 0 : 2 5 мм2. против конкурирующей гипотезы
H 1 : 2 5 мм2.
4.72. На основании контроля n = 12 измерений найдено, что x 70 мм., а S 2,5мм.
Допустив, что ошибка изготовления есть нормальная случайная величина проверить на
уровне значимости 0,05 гипотезу H 0 : 2 7,25 мм2. против конкурирующей
гипотезы H 1 : 2 7,25 мм2.
4.73. На основании контроля n = 6 измерений найдено, что x 70 мм., а S 1,5мм.
Допустив, что ошибка изготовления есть нормальная случайная величина вычислить
мощность критерия при проверке на уровне значимости 0,01 гипотезы
H 0 : 2 3,25 мм2. против конкурирующей гипотезы H 1 : 2 1,25 мм2.
4.74. На основании контроля n = 9 измерений найдено, что x 70 мм., а S 2 мм.
Допустив, что ошибка изготовления есть нормальная случайная величина вычислить
мощность критерия при проверке на уровне значимости 0,05 гипотезы H 0 : 2 5
мм2 против конкурирующей гипотезы H 1 : 2 3 мм2.
4.75. На основании контроля n = 12 измерений найдено, что x 70 мм., а S 2,5мм.
Допустив, что ошибка изготовления есть нормальная случайная величина вычислить
мощность критерия при проверке на уровне значимости 0,1 гипотезы H 0 : 2 7,25
мм2 против конкурирующей гипотезы H 1 : 2 5,25 мм2.
4.76. На основании контроля n = 15 измерений найдено, что x 70 мм., а S 3 мм.
Допустив, что ошибка изготовления есть нормальная случайная величина вычислить
мощность критерия при проверке на уровне значимости 0,02 гипотезы H 0 : 2 10
мм2 против конкурирующей гипотезы H 1 : 2 8 мм2.
4.77. По результатам n = 7 независимых измерений найдено, что x 82,48 мм., а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
30
проверить на уровне значимости 0,05 гипотезу
H 0 : 2 0,01 мм2 против
конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.78. По результатам n = 10 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
проверить на уровне значимости 0,01 гипотезу H 0 : 2 0,01 мм2 против
конкурирующей гипотезы H 1 : 2 0,005 мм2. ответе записать разность между
фактическим и табличным значениями выборочной характеристики.
4.79. По результатам n = 13 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
проверить на уровне значимости 0,02 гипотезу H 0 : 2 0,01 мм2 против
конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.80. По результатам n = 16 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
проверить на уровне значимости 0,1 гипотезу H 0 : 2 0,01 мм2 против
конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.81. По результатам n = 7 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
вычислить мощность критерия при проверке на уровне значимости 0,05 гипотезы
H 0 : 2 0,01 мм2 против конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.82. По результатам n = 10 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
вычислить мощность критерия при проверке на уровне значимости 0,01 гипотезы
H 0 : 2 0,01 мм2 против конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.83. По результатам n = 13 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
вычислить мощность критерия при проверке на уровне значимости 0,02 гипотезы
H 0 : 2 0,01 мм2 против конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.84. По результатам n = 16 независимых измерений найдено, что x 82,48 мм, а
S 0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение
вычислить мощность критерия при проверке на уровне значимости 0,1 гипотезы
H 0 : 2 0,01 мм2 против конкурирующей гипотезы H 1 : 2 0,005 мм2.
4.85. Из продукции двух автоматических линий взяты соответственно выборки
n1 12 и n2 8 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 4 мм2 и 22 9
мм2. Требуется проверить на уровне значимости 0,05 гипотезу H 0 : 1 2 против
H1 : 1 2 .
31
4.86. Из продукции двух автоматических линий взяты соответственно выборки
n1 14 и n2 10 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 5 мм2 и
22 10 мм2. Требуется проверить на уровне значимости 0,015 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.87. Из продукции двух автоматических линий взяты соответственно выборки
n1 16 и n2 12 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 6 мм2 и
22 11 мм2. Требуется проверить на уровне значимости 0,025 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.88. Из продукции двух автоматических линий взяты соответственно выборки
n1 18 и n2 14 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 7 мм2 и
22 12 мм2. Требуется проверить на уровне значимости 0,085 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.89. Из продукции двух автоматических линий взяты соответственно выборки
n1 16 и n2 12 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 6 мм2 и
22 11 мм2. Требуется проверить на уровне значимости 0,05 гипотезу H 0 : 1 2
против H1 : 1 2 .
4.90. Из продукции двух автоматических линий взяты соответственно выборки
n1 12 и n2 8 деталей. По результатам выборочных наблюдений найдены x1 180
мм. и x2 186 мм. Предварительным анализом установлено, что погрешность
изготовления есть нормальные случайные величины с дисперсиями 12 4 мм2 и 22 9
мм2. Требуется проверить на уровне значимости 0,01 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.91. Из двух партий взяты выборки объемом n1 8 и n2 14 деталей. По результатам
выборочных наблюдений найдены x1 252 мм, S 1 2 мм и x2 258 мм, S 2 3 мм.
Предполагая, что погрешность изготовления есть нормальная случайная величина,
проверить на уровне значимости 0,02 гипотезу H 0 : 1 2 против H1 : 1 2 .
4.92. Из двух партий взяты выборки объемом n1 10 и n2 15 деталей. По
результатам выборочных наблюдений найдены x1 254 мм, S 1 3 мм и x2 259 мм,
S 2 4 мм. Предполагая, что погрешность изготовления есть нормальная случайная
32
величина, проверить на уровне значимости 0,01 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.93. Из двух партий взяты выборки объемом n1 12 и n2 16 деталей. По
результатам выборочных наблюдений найдены x1 256 мм, S 1 4 мм и x2 260 мм,
S 2 5 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,05 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.94. Из двух партий взяты выборки объемом n1 14 и n2 17 деталей. По
результатам выборочных наблюдений найдены x1 258 мм, S 1 5 мм и x2 261 мм,
S 2 6 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,001 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.95. Из двух партий взяты выборки объемом n1 16 и n2 18 деталей. По
результатам выборочных наблюдений найдены x1 260 мм, S 1 6 мм и x2 262 мм,
S 2 7 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,01 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.96. Из двух партий взяты выборки объемом n1 8 и n2 14 деталей. По результатам
выборочных наблюдений найдены x1 252 мм. и x2 258 мм. Предварительным
анализом установлено, что средние квадратические отклонения генеральных
совокупностей равны 1 2 мм и 2 3 мм. в предположении о нормальном
распределении проверить на уровне значимости 0,03 гипотезу H 0 : 1 2 против
H1 : 1 2 .
4.97. Из двух партий взяты выборки объемом n1 10 и n2 15 деталей. По
результатам выборочных наблюдений найдены x1 254 мм. и x2 259 мм.
Предварительным анализом установлено, что средние квадратические отклонения
генеральных совокупностей равны 1 3 мм и 2 5 мм. в предположении о
нормальном распределении проверить на уровне значимости 0,02 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.98. Из двух партий взяты выборки объемом n1 12 и n2 16 деталей. По
результатам выборочных наблюдений найдены x1 256 мм. и x2 260 мм.
Предварительным анализом установлено, что средние квадратические отклонения
генеральных совокупностей равны 1 4 мм и 2 7 мм. в предположении о
нормальном распределении проверить на уровне значимости 0,05 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.99. Из двух партий взяты выборки объемом n1 14 и n2 17 деталей. По
результатам выборочных наблюдений найдены x1 258 мм. и x2 261 мм.
33
Предварительным анализом установлено, что средние квадратические отклонения
генеральных совокупностей равны 1 5 мм и 2 9 мм. в предположении о
нормальном распределении проверить на уровне значимости 0,01 гипотезу
H 0 : 1 2 против H1 : 1 2 .
4.100. Из двух партий взяты выборки объемом n1 8 и n2 14 деталей. По результатам
выборочных наблюдений найдены x1 252 мм, S 1 2 мм и x2 258 мм, S 2 3 мм.
Предполагая, что погрешность изготовления есть нормальная случайная величина,
проверить на уровне значимости 0,05 гипотезу о равенстве дисперсий двух
генеральных совокупностей H 0 : 12 22 .
4.101. Из двух партий взяты выборки объемом n1 10 и n2 15 деталей. По
результатам выборочных наблюдений найдены x1 254 мм, S 1 3 мм и x2 259 мм,
S 2 4 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,05 гипотезу о равенстве дисперсий
двух генеральных совокупностей H 0 : 12 22 .
4.102. Из двух партий взяты выборки объемом n1 12 и n2 16 деталей. По
результатам выборочных наблюдений найдены x1 256 мм, S 1 4 мм и x2 260 мм,
S 2 5 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,01 гипотезу о равенстве дисперсий
двух генеральных совокупностей H 0 : 12 22 .
4.103. Из двух партий взяты выборки объемом n1 14 и n2 17 деталей. По
результатам выборочных наблюдений найдены x1 258 мм, S 1 5 мм и x2 261 мм,
S 2 6 мм. Предполагая, что погрешность изготовления есть нормальная случайная
величина, проверить на уровне значимости 0,001 гипотезу о равенстве дисперсий
двух генеральных совокупностей H 0 : 12 22 .
4.104. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 51, 49, 52 и 48 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,01
гипотезу о равенстве дисперсий двух генеральных совокупностей.
4.105. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 50, 48, 52 и 46 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,05
гипотезу о равенстве дисперсий двух генеральных совокупностей.
4.106. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 49, 47, 52 и 44 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,01
гипотезу о равенстве дисперсий двух генеральных совокупностей.
4.107. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 48, 46, 52 и 42 кг. В
34
предположении о нормальном распределении проверить на уровне значимости
0,001 гипотезу о равенстве дисперсий двух генеральных совокупностей.
4.108. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 51, 49, 52 и 48 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,02
гипотезу о равенстве двух генеральных средних H 0 : 1 2 против конкурирующей
гипотезы H1 : 1 2 . Предполагается, что 1 2 .
4.109. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 50, 48, 52 и 46 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,05
гипотезу о равенстве двух генеральных средних H 0 : 1 2 против конкурирующей
гипотезы H1 : 1 2 . Предполагается, что 1 2 .
4.110. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 49, 47, 52 и 44 кг. В
предположении о нормальном распределении проверить на уровне значимости 0,01
гипотезу о равенстве двух генеральных средних H 0 : 1 2 против конкурирующей
гипотезы H1 : 1 2 . Предполагается, что 1 2 .
4.111. Выборочное обследование показало, что на изготовление одного изделия первая
бригада затрачивала 40, 47, 43, 44 и 46 кг сырья, а вторая – 48, 46, 52 и 42 кг. В
предположении о нормальном распределении проверить на уровне значимости
0,001 гипотезу о равенстве двух генеральных средних H 0 : 1 2 против
конкурирующей гипотезы H1 : 1 2 . Предполагается, что 1 2 .
4.112. Из продукции первой смены случайным образом отобрано n1 150 деталей, а из
второй - n2 100 деталей. Из отобранных деталей дефектными оказались m1 15 и
m2 14. проверить на уровне значимости 0,05 гипотезу о равенстве вероятностей
появления дефектного изделия, т.е. H 0 : p1 p2 .
4.113. Из продукции первой смены случайным образом отобрано n1 150 деталей, а из
второй - n2 100 деталей. Из отобранных деталей дефектными оказались m1 19 и
m2 19. проверить на уровне значимости 0,01 гипотезу о равенстве вероятностей
появления дефектного изделия, т.е. H 0 : p1 p2 .
4.114. Из продукции первой смены случайным образом отобрано n1 150 деталей, а из
второй - n2 100 деталей. Из отобранных деталей дефектными оказались m1 23 и
m2 24. проверить на уровне значимости 0,02 гипотезу о равенстве вероятностей
появления дефектного изделия, т.е. H 0 : p1 p2 .
4.115. Из продукции первой смены случайным образом отобрано n1 150 деталей, а из
второй - n2 100 деталей. Из отобранных деталей дефектными оказались m1 27 и
m2 29. проверить на уровне значимости 0,005 гипотезу о равенстве вероятностей
появления дефектного изделия, т.е. H 0 : p1 p2 .
35
4.116. Из 200 задач первого типа, предложенных для решения, студенты решили
m1 132, а из n2 250 задач второго типа студенты решили m2 120 задач. Проверить
на уровне значимости 0,02 гипотезу о том, что вероятность решения задачи не
зависит от того, к какому типу она относится, т.е H 0 : p1 p2 .
4.117. Из 200 задач первого типа, предложенных для решения, студенты решили
m1 142, а из n2 250 задач второго типа студенты решили m2 125 задач. Проверить
на уровне значимости 0,01 гипотезу о том, что вероятность решения задачи не
зависит от того, к какому типу она относится, т.е H 0 : p1 p2 .
4.118. Из 200 задач первого типа, предложенных для решения, студенты решили
m1 152, а из n2 250 задач второго типа студенты решили m2 130 задач. Проверить
на уровне значимости 0,05 гипотезу о том, что вероятность решения задачи не
зависит от того, к какому типу она относится, т.е H 0 : p1 p2 .
4.119. Из 200 задач первого типа, предложенных для решения, студенты решили
m1 162, а из n2 250 задач второго типа студенты решили m2 135 задач. Проверить
на уровне значимости 0,01 гипотезу о том, что вероятность решения задачи не
зависит от того, к какому типу она относится, т.е H 0 : p1 p2 .
36
Варианты индивидуальных контрольных заданий по
статистическому оцениванию
Номер
варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
1
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.10.
1.12.
1.14.
1.15.
1.17.
1.18.
1.21.
1.22.
1.23.
1.24.
1.26.
1.28.
1.29.
1.30.
1.31.
1.32.
1.33.
1.36.
1.37.
1.39.
1.41.
1.42.
1.7.
1.29.
1.31.
1.12.
2
2.1.
2.5.
2.7.
2.23.
2.20.
2.12.
2.29.
2.38.
2.44.
2.18.
2.25.
2.32.
2.40.
2.48.
2.2.
2.6.
2.8.
2.41.
2.21.
2.13.
2.30.
2.27.
2.45.
2.19.
2.42.
2.34.
2.3.
2.22.
2.6.
2.40.
2.1.
2.20.
Номера задач
3
4
5
3.16. 3.40. 3.71.
3.19. 3.44. 3.74.
3.22. 3.48. 3.78.
3.27. 3.52. 3.82.
3.30. 3.55. 3.89.
3.34. 3.59. 3.93.
3.37. 3.63. 3.97.
3.17. 3.67. 3.89.
3.20. 3.41. 3.72.
3.23. 3.45. 3.75.
3.28. 3.49. 3.79.
3.31. 3.53. 3.83.
3.35. 3.56. 3.90.
3.38. 3.60. 3.94.
3.24. 3.64. 3.98.
3.16. 3.68. 3.86.
3.19. 3.42. 3.76.
3.22. 3.46. 3.80.
3.27. 3.50. 3.91.
3.30. 3.57. 3.95.
3.34. 3.61. 3.99.
3.37. 3.65. 3.87.
3.17. 3.69. 3.71.
3.20. 3.40. 3.74.
3.23. 3.44. 3.78.
3.28. 3.48. 3.82.
3.31. 3.52. 3.89.
3.35. 3.55. 3.93.
3.16. 3.49. 3.74.
3.24. 3.40. 3.98.
3.19. 3.53. 3.71.
3.27. 3.55. 3.83.
37
6
3.100.
3.103.
3.112.
3.115.
3.106.
3.109.
3.118.
3.121.
3.101.
3.104.
3.113.
3.116.
3.107.
3.110.
3.119.
3.122.
3.102.
3.105.
3.114.
3.117.
3.108.
3.111.
3.120.
3.123.
3.100.
3.103.
3.112.
3.115.
3.106.
3.103.
3.121.
3.118.
7
3.124.
3.128.
3.140.
3.143.
3.125.
3.129.
3.141.
3.144.
3.126.
3.130.
3.142.
3.145.
3.127.
3.131.
3.146.
3.124.
3.128.
3.140.
3.143.
3.125.
3.129.
3.141.
3.144.
3.126.
3.130.
3.142.
3.145.
3.127.
3.131.
3.146.
3.124.
3.127.
Варианты индивидуальных контрольных заданий по
статистической проверке гипотез
Номер
варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
1
4.29.
4.30.
4.31.
4.32.
4.37.
4.38.
4.39.
4.40.
4.41.
4.42.
4.43.
4.48.
4.49.
4.50.
4.51.
4.52.
4.53.
4.54.
4.59.
4.60.
4.61.
4.62.
4.29.
4.30.
4.31.
4.32.
4.37.
4.38.
4.49.
4.50.
4.51.
4.52.
2
4.55.
4.56.
4.57.
4.58.
4.63.
4.64.
4.65.
4.66.
4.56.
4.57.
4.58.
4.33.
4.34.
4.35.
4.36.
4.44.
4.45.
4.46.
4.47.
4.33.
4.34.
4.35.
4.55.
4.56.
4.57.
4.68.
4.63.
4.64.
4.36.
4.44.
4.45.
4.46.
Номера задач
3
4
5
4.67. 4.84. 4.85.
4.68. 4.83. 4.86.
4.69. 4.82. 4.87.
4.70. 4.81. 4.88.
4.71. 4.77. 4.89.
4.72. 4.76. 4.90.
4.73. 4.75. 4.96.
4.77. 4.74. 4.97.
4.78. 4.75. 4.98.
4.79. 4.76. 4.99.
4.80. 4.77. 4.85.
4.100. 4.81. 4.86.
4.101. 4.82. 4.87.
4.102. 4.83. 4.88.
4.103. 4.84. 4.89.
4.104. 4.74. 4.90.
4.105. 4.75. 4.96.
4.106. 4.76. 4.97.
4.107. 4.77. 4.98.
4.67. 4.81. 4.99.
4.68. 4.82. 4.85.
4.69. 4.83. 4.86.
4.70. 4.84. 4.87.
4.71. 4.75. 4.88.
4.72. 4.76. 4.89.
4.73. 4.77. 4.90.
4.77. 4.81. 4.96.
4.78. 4.82. 4.97.
4.79. 4.83. 4.98.
4.80. 4.74. 4.99.
4.100. 4.75. 4.85.
4.101. 4.76. 4.86.
38
6
4.91.
4.92.
4.93.
4.94.
4.95.
4.108.
4.109.
4.110.
4.111.
4.91.
4.92.
4.93.
4.94.
4.95.
4.108.
4.109.
4.110.
4.111.
4.91.
4.92.
4.93.
4.94.
4.95.
4.108.
4.109.
4.110.
4.111.
4.91.
4.92.
4.93.
4.94.
4.95.
7
4.112.
4.113.
4.114.
4.115.
4.116.
4.117.
4.118.
4.119.
4.112.
4.113.
4.114.
4.115.
4.116.
4.117.
4.118.
4.119.
4.112.
4.113.
4.114.
4.115.
4.116.
4.117.
4.118.
4.119.
4.112.
4.113.
4.114.
4.115.
4.116.
4.117.
4.118.
4.119.
8
4.2.
4.6.
4.10.
4.14.
4.18.
4.22.
4.26.
4.3.
4.7.
4.11.
4.15.
4.19.
4.23.
4.27.
4.4.
4.8.
4.12.
4.16.
4.20.
4.24.
4.28.
4.2.
4.6.
4.10.
4.14.
4.18.
4.22.
4.26.
4.5.
4.9.
4.17.
4.25.
МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Методические указания к использованию некоторых таблиц
2
2 t x2
(t )
dx
e
0
2
В таблице 1 протабулирована функция:
f(t) - плотность нормированной нормально распределенной случайной величины T
N(0,1)
Вероятность попадания случайной величины Т в интервал от t1 до t2
вычисляется по формуле: P(t T t ) 1 [(t ) (t )] , где Ф(t) обладает
1
2
2
2
1
следующими свойствами: Ф(-t) = - Ф(t); Ф( ) = 1; Ф(3) = 0,9973.
Пример:
1
1
P(1,36 T 2,15) [(2.15) (1.36)] [0.9684 0.8262] 0.8973
2
2
В таблице 2 протабулирована вероятность выхода за пределы интервала от -t до
+t случайной величины, имеющей распределение Стьюдента (t - распределение) с
числом степеней свободы :
St (t; ) P( T t )
f (t; ) - плотность распределения Стьюдента с числом степеней свободы .
f(t;
f(t)
Ф(t)
-t
0
t
-t
Т
39
0
t
Т
Вероятность попадания случайной величины T в интервал от t1 до t2
вычисляется по формуле:
1
P(t1 T t2 ) [St (t1) St (t2 )]
2
.
Функция St(t) обладает следующими свойствами: St(-t) = 2 - St(t); St ( ) = 0; St (- )
= 2; St (0) = 1.
Пример: при = 10 определить
1
1
P(1,36 T 2,15) [St (1,36) St (2,15)] [2 St (1,36)
2
2
1
1
St (2,15)] [2 St (1,372) St (2,228)] [2 0,2 0,05] 0,875
2
2
Чтобы не прибегать к интерполяции, в строке, соответствующей =10, мы взяли
ближайшие к заданным значениям 1,36 и 2,15.
Каждая строка таблицы отвечает t-распределению, с соответствующим числом
степеней свободы .
В таблице 3 протабулирована вероятность того, что наблюдаемое значение
случайной величины 2 , имеющей распределение Пирсона (хи-квадрат распределение)
с числом степеней свободы , превысит табличное значение 2 табл.
2
f (Х ;
2
;
Рi (Х табл
Х2
Х2табл
На рис. 3 представлен график функции f(Х2табл) - плотности
распределения с числом степеней свободы .
2
f ( табл; y) - плотность 2 - распределения с числом степеней свободы .
Вероятность попадания случайной величины 2 в интервал от 12 до 22
вычисляется по формуле
0
P(12 2 22 ) P( 2 12 ) P( 2 22 ) Pi (12 ) Pi ( 22 )
2 -
.
) обладает следующими свойствами:
Функция Pi (
Pi (0) = 1; Pi ( ) = 0.
2
табл
Пример: при =10 определить
P(2,5 2 19,0) Pi (2,5) Pi (19,0) Pi (2,558) Pi (18,307)
0,99 0,05 0,94
Чтобы не прибегать к интерполяции в строке таблицы, соответствующей =10,
мы взяли ближайшие к заданным значениям 2,5 и 19,0.
Каждая строка таблицы отвечает 2 - распределению с соответствующим
числом степеней свободы .
40
В таблице 4 для случайной величины F, имеющей закон распределения ФишераСнедекора (F-распределение) с числами степеней свободы числителя 1 и знаменателя
2 , протабулированы три табличных значения, соответствующие трем вероятностям
(уровням значимости): P( F Fтабл ) = 0,05; 0,01 и 0,001.
Пример: Уровню значимости α = 0,01 и числам степеней свободы числителя 1 =5 и
знаменателя 2 =7 соответствует Fтабл=7,46.
Статистика F строится таким образом, чтобы наблюдаемое значение было не меньше
единицы.
41
Таблица 1
Нормальный закон распределения
Целые и десятичные доли
0
t
0,0
0,0000
0,1
0797
0,2
1585
0,3
2358
0,4
3108
0,5
3829
0,6
4515
0,7
5161
0,8
5763
0,9
6319
1,0
0,6827
1,1
7287
1,2
7699
1,3
8064
1,4
8385
1,5
8664
1,6
8904
1,7
9109
1,8
9281
1,9
9426
1
2
0,0080
0876
1663
2434
3182
3899
4581
5223
5821
6372
0,6875
7330
7737
8098
8415
8690
8926
9127
9297
9439
0,0160
0955
1741
2510
3255
3969
4647
5285
5878
6424
0,6923
7373
7775
8132
8444
8715
8948
9146
9312
9451
З н а ч е н и я ф у н к ц и и Ф(t) = P (|T| tтабл)
Сотые доли t
3
4
5
6
0,0239
1034
1819
2586
3328
4039
4713
5346
5935
6476
0,6970
7415
7813
8165
8473
8740
8969
9164
9327
9464
0,0319
1113
1897
2661
3401
4108
4778
5407
5991
6528
0,7017
7457
7850
8198
8501
8764
8990
9181
9342
9476
42
0,0399
1192
1974
2737
3473
4177
4843
5467
6047
6579
0,7063
7499
7887
8230
8529
8789
9011
9199
9357
9488
0,0478
1271
2051
2812
3545
4245
4907
5527
6102
6629
0,7109
7540
7923
8262
8557
8812
9031
9216
9371
9500
7
8
9
0,0558
1350
2128
2886
3616
4313
4971
5587
6157
6679
0,7154
7580
7959
8293
8584
8836
9051
9233
9385
9512
0,0638
1428
2205
2960
3688
4381
5035
5646
6211
6729
0,7199
7620
7994
8324
8611
8859
9070
9249
9399
9523
0,0717
1507
2282
3035
3759
4448
5098
5705
6265
6778
0,7243
7660
8029
8355
8638
8882
9090
9265
9412
9534
Окончание табл. 1
Целые и
десятичные
0
доли t
2,0
0,9545
2,1
9643
2,2
9722
2,3
9786
2,4
9836
2,5
9876
2,6
9907
2,7
9931
2,8
9949
2,9
9963
3,0
0,9973
3,1
9981
3,2
9986
3,3
9990
3,4
9993
3,5
9995
3,6
9997
3,7
9998
3,8
9999
3,9
9999
4,0
0,999936
4,5
0,999994
5,0
0,99999994
Сотые доли t
1
2
3
4
5
6
7
8
9
0,9556
9651
9729
9791
9841
9879
9910
9933
9951
9964
0,9974
9981
9987
9991
9994
9996
9997
9998
9999
9999
9999
-
0,9566
9660
9736
9797
9845
9883
9912
9935
9952
9965
0,9975
9982
9987
9991
9994
9996
9997
9998
9999
9999
9999
-
0,9576
9668
9743
9802
9849
9886
9915
9937
9953
9966
0,9976
9983
9988
9991
9994
9996
9997
9998
9999
9999
9999
-
0,9586
9676
9749
9807
9853
9889
9917
9939
9955
9967
0,9976
9983
9988
9992
9994
9996
9997
9998
9999
9999
9999
-
0,9596
9684
9756
9812
9857
9892
9920
9940
9956
9968
0,9977
9984
9988
9992
9994
9996
9997
9998
9999
9999
9999
-
0,9606
9692
9762
9817
9861
9895
9922
9942
9958
9969
0,9978
9984
9989
9992
9995
9996
9997
9998
9999
9999
9999
-
0,9616
9700
9768
9822
9865
9898
9924
9944
9959
9970
0,9979
9985
9989
9992
9995
9996
9998
9998
9999
9999
9999
-
0,9625
9707
9774
9827
9869
9901
9926
9946
9960
9971
0,9979
9985
9990
9993
9995
9997
9998
9998
9999
9999
9999
-
0,9634
9715
9780
9832
9872
9904
9928
9947
9961
9972
0,9980
9986
9990
9993
9995
9997
9998
9998
9999
9999
9999
-
43
Таблица 2
Р а с п р е д е л е н и е С т ь ю д е н т а (t-распределение)
В е р о я т н о с т ь St (t) = P (|T| > tтабл)
0,5
0,4
0,3
0,2
0,1
1,000
1,376
1,963
3,078
6,314
0,816
1,061
1,386
1,886
2,920
0,765
0,978
1,250
1,638
2,353
0,741
0,941
1,190
1,533
2,132
0,727
0,920
1,156
1,476
2,015
1
2
3
4
5
0,9
0,158
0,142
0,137
0,134
0,132
0,8
0,325
0,289
0,277
0,271
0,267
0,7
0,510
0,445
0,424
0,414
0,408
0,6
0,727
0,617
0,584
0,569
0,559
6
7
8
9
10
0,131
0,130
0,130
0,129
0,129
0,265
0,263
0,262
0,261
0,260
0,404
0,402
0,399
0,398
0,327
0,553
0,549
0,546
0,543
0,542
0,718
0,711
0,706
0,703
0,700
0,906
0,896
0,889
0,883
0,879
1,134
1,119
1,108
1,100
1,093
1,440
1,415
1,397
1,383
1,372
1,943
1,895
1,860
1,833
1,812
2,447
2,365
2,306
2,262
2,228
3,143
2,998
2,896
2,821
2,764
3,707
3,499
3,355
3,250
3,169
5,959
5,405
5,041
4,781
4,583
11
12
13
14
15
0,129
0,128
0,128
0,128
0,128
0,260
0,259
0,259
0,258
0,258
0,396
0,395
0,394
0,393
0,393
0,540
0,539
0,538
0,537
0,536
0,697
0,695
0,694
0,692
0,691
0,876
0,873
0,870
0,868
0,866
1,088
1,083
1,079
1,076
1,074
1,363
1,356
1,350
1,345
1,341
1,796
1,782
1,771
1,761
1,753
2,201
2,179
2,160
2,145
2,131
2,718
2,681
2,650
2,624
2,602
3,106
3,055
3,012
2,977
2,947
4,437
4,318
4,221
4,140
4,073
16
17
18
19
20
0,128
0,128
0,127
0,127
0,127
0,258
0,257
0,257
0,257
0,257
0,392
0,392
0,392
0,391
0,391
0,535
0,534
0,534
0,533
0,533
0,690
0,689
0,688
0,688
0,687
0,865
0,863
0,862
0,861
0,860
1,071
1,069
1,067
1,066
1,064
1,337
1,333
1,330
1,328
1,325
1,746
1,740
1,734
1,729
1,725
2,120
2,110
1,101
2,093
2,086
2,583
2,567
2,552
2,539
2,528
2,921
2,898
2,878
2,861
2,845
4,015
3,965
3,922
3,833
3,850
44
0,05
0,02
0,01
0,001
12,706 31,821 63,657 636,619
4,303 6,965 9,925 31,598
3,182 4,541 5,841 12,941
2,776 3,747 4,604
8,610
2,571 3,365 4,043
6,859
Окончание табл. 2
В е р о я т н о с т ь St (t) = P (|T| > tтабл)
21
22
23
24
25
0,9
0,127
0,127
0,127
0,127
0,127
0,8
0,257
0,256
0,256
0,256
0,256
0,7
0,391
0,390
0,390
0,390
0,390
0,6
0,532
0,532
0,532
0,531
0,531
0,5
0,686
0,686
0,685
0,685
0,684
0,4
0,859
0,858
0,868
0,857
0,856
0,3
1,063
1,061
1,060
1,059
1,058
0,2
1,323
1,321
1,319
1,318
1,316
0,1
1,721
1,717
1,714
1,711
1,708
0,05
2,080
2,074
2,069
2,064
2,060
0,02
2,518
2,508
2,500
2,402
2,485
0,01
2,831
2,819
2,807
2,797
2,787
0,001
3,819
3,792
3,767
3,745
3,725
26
27
28
29
30
0,127
0,127
0,127
0,127
0,127
0,256
0,256
0,256
0,256
0,256
0,390
0,389
0,389
0,389
0,389
0,531
0,531
0,530
0,530
0,530
0,684
0,684
0,683
0,683
0,683
0,856
0,855
0,855
0,854
0,854
1,058
1,057
1,056
1,055
1,055
1,315
1,314
1,313
1,311
1,310
1,706
1,703
1,701
1,699
1,697
2,056
2,052
2,048
2,045
2,042
2,479
2,473
2,467
2,462
2,457
2,779
2,771
2,763
2,756
2,750
3,707
3,690
3,674
3,659
3,646
40
60
120
0,126
0,126
0,126
0,126
0,255
0,254
0,254
0,253
0,388
0,387
0,386
0,385
0,529
0,527
0,526
0,524
0,681
0,679
0,677
0,674
0,851
0,848
0,845
0,842
1,050
1,046
1,041
1,036
1,303
1,296
1,289
1,282
1,684
1,671
1,658
1,645
2,021
2,000
1,980
1,960
2,423
2,390
2,358
2,326
2,704
2,660
2,617
2,576
3,551
3,460
3,373
3,291
45
Таблица 3
Р а с п р е д е л е н и е П и р с о н а (2-распределение)
Значения 2табл для вероятностей Р (2 > 2табл)
Вероятность
0,975
0,95
0,03982
0,00393
0,0506
0,103
0,216
0,352
0,484
0,711
0,831
1,145
1
2
3
4
5
0,999
0,05157
0,00200
0,0243
0,0908
0,210
0,995
0,04393
0,0100
0,0717
0,207
0,412
0,99
0,03157
0,0201
0,115
0,297
0,554
0,98
0,03628
0,0404
0,185
0,429
0,752
0,90
0,0158
0,211
0,584
1,064
1,610
0,80
0,0642
0,446
1,005
1,649
2,343
0,75
0,102
0,575
1,213
1,923
2,675
0,70
0,148
0,713
1,424
2,195
3,000
0,50
0,455
1,386
2,366
3,357
4,351
6
7
8
9
10
0,381
0,598
0,857
1,152
1,479
0,676
0,989
1,344
1,735
2,156
0,872
1,239
1,646
2,088
2,558
1,134
1,564
2,032
2,532
3,059
1,237
1,690
2,180
2,700
3,247
1,635
2,167
2,733
3,325
3,240
2,204
2,833
3,490
4,168
4,865
3,070
3,822
4,594
5,380
6,179
3,455
4,255
5,071
5,899
6,737
3,828
4,671
5,527
6,393
7,267
5,348
6,346
7,344
8,343
9,342
11
12
13
14
15
1,834
2,214
2,617
3,041
3,483
2,603
3,074
3,565
4,075
4,601
3,053
3,571
4,107
4,660
5,229
3,609
4,178
4,765
5,368
5,985
3,816
4,404
5,009
5,629
6,262
4,575
5,226
5,892
6,571
7,261
5,578
6,304
7,042
7,790
8,547
6,989
7,807
8,634
9,467
10,307
7,584
8,438
9,299
10,165
11,036
8,148
9,034
9,926
10,821
11,721
10,341
11,340
12,340
13,339
14,339
16
17
18
19
20
3,942
4,416
4,905
5,407
5,921
5,142
5,697
6,265
6,844
7,434
5,812
6,408
7,015
7,633
8,260
6,614
7,255
7,906
8,567
9,237
6,908
7,564
8,231
8,907
9,591
7,962
8,672
9,390
10,117
10,871
9,312
10,085
10,865
11,651
12,443
11,152
12,002
12,857
13,716
14,578
11,912
12,892
13,675
14,562
15,452
12,624
13,531
14,440
15,352
16,266
15,338
16,338
17,338
18,338
19,337
21
22
23
24
25
6,447
6,983
7,529
8,035
8,649
8,034
8,643
9,260
9,886
10,520
8,897
9,542
10,196
10,856
11,524
9,915
10,600
11,293
11,992
12,697
10,283
10,982
11,688
12,401
13,120
11,591
12,338
13,091
13,848
14,611
13,240
14,041
14,848
15,659
16,173
15,445
16,314
17,187
18,062
18,940
16,344
17,240
18,137
19,037
19,939
17,182
18,101
19,021
19,943
20,887
20,337
21,337
22,337
23,337
24,337
26
27
28
29
30
9,222
9,803
10,391
10,986
11,588
11,160
11,808
12,461
13,121
13,787
12,198
12,879
13,565
14,256
14,953
13,409
14,125
14,847
15,574
16,306
13,844
14,573
15,308
16,047
16,791
15,379
16,151
16,928
17,708
18,493
17,292
18,114
18,937
19,768
20,599
19,820
20,703
21,588
22,475
23,364
20,843
21,749
22,657
23,567
24,478
21,792
22,719
23,617
24,577
25,508
25,336
26,136
27,336
28,336
29,336
46
Окончание табл. 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,30
1,074
2,408
3,665
4,878
6,064
7,231
8,383
9,524
10,656
11,781
12,899
14,011
15,119
16,222
17,322
18,418
19,511
20,601
21,689
22,775
23,858
24,939
26,018
27,096
28,172
29,246
30,319
31,391
32,461
33,530
0,25
1,323
2,773
4,108
5,385
6,626
7,841
9,037
10,219
11,389
12,549
13,701
14,845
15,984
17,117
18,245
19,369
20,489
21,605
22,718
23,828
24,935
26,039
27,141
28,241
29,339
30,434
31,528
32,620
33,711
34,800
0,20
1,642
3,219
4,642
5,989
7,289
8,558
9,803
11,030
12,242
13,412
14,631
15,812
16,985
18,151
19,311
20,465
21,615
22,760
23,900
25,038
26,171
27,301
28,429
29,553
30,675
31,795
32,912
34,027
35,139
36,250
0,10
2,706
4,605
6,251
7,779
9,236
10,645
12,017
13,362
14,684
15,987
17,275
18,549
19,812
21,064
22,307
23,542
24,769
25,989
27,204
28,412
29,615
30,813
32,007
33,196
34,382
35,563
36,741
37,916
39,087
40,256
Вероятность
0,05
0,025
3,841
5,024
5,991
7,378
7,815
9,348
9,488
11,143
11,070
12,839
12,592
14,449
14,067
16,013
15,507
17,535
16,919
19,023
18,307
20,483
19,675
21,920
21,026
23,337
22,362
24,736
23,685
26,119
24,996
27,488
26,296
28,845
27,587
30,191
28,869
31,526
30,144
32,852
31,410
34,170
32,671
35,479
33,924
36,781
35,172
38,076
36,415
39,364
37,652
40,046
38,885
41,923
40,113
43,194
41,337
44,461
42,557
45,722
43,773
46,979
47
0,02
5,412
7,824
9,837
11,668
13,388
15,033
16,622
18,168
19,679
21,161
22,618
24,054
25,472
26,873
28,259
29,633
30,995
32,346
33,687
35,020
36,343
37,659
38,968
40,270
41,566
42,856
44,140
45,419
46,693
47,962
0,01
6,635
9,210
11,345
13,277
15,086
16,812
18,475
20,090
21,666
23,209
24,725
26,217
27,688
29,141
30,578
32,000
33,409
34,805
36,191
37,566
38,932
40,289
41,638
42,980
44,314
45,642
46,963
48,278
49,588
50,892
0,005
7,879
10,597
12,838
14,860
16,750
18,548
20,278
21,955
23,589
25,188
26,757
28,300
29,819
31,319
32,801
34,267
35,718
37,156
38,582
39,997
41,401
42,796
44,181
45,558
46,928
48,290
49,645
50,993
52,336
53,672
0,001
10,827
13,815
16,268
18,465
20,517
22,457
24,322
26,125
27,877
29,588
31,264
32,909
34,528
36,123
37,697
39,252
40,790
42,312
43,820
45,315
46,797
48,268
49,728
51,170
52,620
54,052
55,476
56,893
58,302
59,703
Таблица 4
Р а с п р е д е л е н и е Ф и ш е р а - С н е д е к о р а (F-распределение)
Значения Fтабл, удовлетворяющие условию P (F > Fтабл). Первое значение соответствует вероятности 0,05,
второе - вероятности 0,01 и третье - вероятности 0,001, где 1 - число
степеней свободы числителя, а 2 - число степеней свободы знаменателя.
1
1
2
3
4
5
6
8
12
24
t
1
161,4
4052
406523
199,5
4999
500016
215,7
5403
536700
224,6
5625
562527
230,2
5764
576449
234,0
5859
585953
238,9
5981
598149
243,9
6106
610598
249,0
6234
623432
253,3
6366
636535
12,71
63,66
636,2
2
18,51
98,49
998,46
19,00
99,01
999,00
19,16
00,17
999,20
19,25
99,25
999,20
19,30
99,30
999,20
19,33
99,33
999,20
19,37
99,36
999,40
19,41
99,42
999,60
19,45
99,46
999,40
19,50
99,50
999,40
4,30
9,92
31,00
3
10,13
34,12
67,47
9,55
30,81
148,51
9,28
29,46
141,10
9,12
28,71
137,10
9,01
28,24
134,60
8,94
27,91
132,90
8,84
27,49
130,60
8,74
27,05
128,30
8,64
26,60
125,90
8,53
26,12
123,50
3,18
5,84
12,94
4
7,71
21,20
74,13
6,94
18,00
61,24
6,59
16,69
56,18
6,39
15,98
53,43
6,26
15,52
51,71
6,16
15,21
50,52
6,04
14,80
49,00
5,91
14,37
47,41
5,77
13,93
45,77
5,63
13,46
44,05
2,78
4,60
8,61
5
6,61
16,26
47,04
5,79
13,27
36,61
5,41
12,06
33,20
5,19
11,39
31,09
5,05
10,97
20,75
4,95
10,67
28,83
4,82
10,27
27,64
4,68
9,89
26,42
4,53
9,47
25,14
4,36
9,02
23,78
2,57
4,03
6,86
6
5,99
13,74
35,51
5,14
10,92
26,99
4,76
9,78
23,70
4,53
9,15
21,90
4,39
8,75
20,81
4,28
8,47
20,03
4,15
8,10
19,03
4,00
7,72
17,99
3,84
7,31
16,89
3,67
6,88
15,75
2,45
3,71
5,96
7
5,59
12,25
29,22
4,74
9,55
21,69
4,35
8,45
18,77
4,12
7,85
17,19
3,97
7,46
16,21
3,87
7,19
15,52
3,73
6,84
14,63
3,57
6,47
13,71
3,41
6,07
12,73
3,23
5,65
11,70
2,36
3,50
5,40
2
48
Продолжение табл. 4
1
2
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
8
12
24
t
5,32
11,26
25,42
5,12
10,56
22,86
4,96
10,04
21,04
4,84
9,65
19,69
4,75
9,33
18,64
4,67
9,07
17,81
4,60
8,86
17,14
4,45
8,68
16,59
4,41
8,53
16,12
4,46
8,65
18,49
4,26
8,02
16,39
4,10
7,56
14,91
3,98
7,20
13,81
3,88
6,93
12,98
3,80
6,70
12,31
3,74
6,51
11,78
3,68
6,36
11,34
3,63
6,23
10,97
4,07
7,59
15,83
3,86
6,99
13,90
3,71
6,55
12,55
3,59
6,22
11,56
3,49
5,95
10,81
3,41
5,74
10,21
3,34
5,56
9,73
3,29
5,42
9,34
3,24
5,29
9,01
3,84
7,10
14,39
3,63
6,42
12,56
3,48
5,99
11,28
3,36
5,67
10,35
3,26
5,41
9,63
3,18
5,20
9,07
3,11
5,03
8,62
3,06
4,89
8,25
3,01
4,77
7,94
3,69
6,63
13,49
3,48
6,06
11,71
3,33
5,64
10,48
3,20
5,32
9,58
3,11
5,06
8,89
3,02
4,86
8,35
2,96
4,69
7,92
2,90
4,56
7,57
2,85
4,44
7,27
3,58
6,37
12,86
3,37
5,80
11,13
3,22
5,39
9,92
3,09
5,07
9,05
3,00
4,82
8,38
2,92
4,62
7,86
2,85
4,46
7,44
2,79
4,32
7,09
2,74
4,20
6,80
3,44
6,03
12,04
3,23
5,47
10,37
3,07
5,06
9,20
2,95
4,74
8,35
2,85
4,50
7,71
2,77
4,30
7,21
2,70
4,14
6,80
2,64
4,00
6,47
2,59
3,89
6,20
3,28
5,67
11,19
3,07
5,11
9,57
2,91
4,71
8,45
2,79
4,40
7,62
2,69
4,16
7,00
2,60
3,96
6,52
2,53
3,80
6,13
2,48
3,67
5,81
2,42
3,55
5,55
3,12
5,28
10,30
2,90
4,73
8,72
2,74
4,33
7,64
2,61
4,02
6,85
2,50
3,78
6,25
2,42
3,59
5,78
2,35
3,43
5,41
2,29
3,29
5,10
2,24
3,18
4,85
2,99
4,86
9,35
2,71
4,31
7,81
2,54
3,91
6,77
2,40
3,60
6,00
2,30
3,36
5,42
2,21
3,16
4,97
2,13
3,00
4,60
2,07
2,87
4,31
2,01
2,75
4,06
2,31
3,36
5,04
2,26
3,25
4,78
2,23
3,17
4,59
2,20
3,11
4,49
2,18
3,06
4,32
2,16
3,01
4,12
2,14
2,98
4,14
2,13
2,95
4,07
2,12
2,92
4,02
49
1
2
3
4
5
6
8
12
Продолжение табл. 4
24
t
4,45
8,40
15,72
4,41
8,28
15,38
3,59
6,11
10,66
3,55
6,01
10,39
3,20
5,18
8,73
3,16
5,09
8,49
2,96
4,67
7,68
2,93
4,58
7,46
2,81
4,34
7,02
2,77
4,25
6,81
2,70
4,10
6,56
2,66
4,01
6,35
2,55
3,79
5,96
2,51
3,71
5,76
2,38
3,45
5,32
2,34
3,37
5,13
2,19
3,08
4,63
2,15
3,01
4,45
1,96
2,65
3,85
1,92
2,57
3,67
2,11
2,90
3,96
2,10
2,88
3,92
19
4,38
8,18
15,08
3,52
5,93
10,16
3,13
5,01
8,28
2,90
4,50
7,26
2,74
4,17
6,61
2,63
3,94
6,18
2,48
3,63
5,59
2,31
3,30
4,97
2,11
2,92
4,29
1,88
2,49
3,52
2,09
2,86
3,88
20
4,35
8,10
14,82
3,49
5,85
9,95
3,10
4,94
8,10
2,87
4,43
7,10
2,71
4,10
6,46
2,60
3,87
6,02
2,45
3,56
5,44
2,28
3,23
4,82
2,08
2,86
4,15
1,84
2,42
3,38
2,09
2,84
3,85
21
4,32
8,02
14,62
3,47
5,78
9,77
3,07
4,87
7,94
2,84
4,37
6,95
2,68
4,04
6,32
2,57
3,81
5,88
2,42
3,51
5,31
2,25
3,17
4,70
2,05
2,80
4,03
1,82
2,36
3,26
2,08
2,83
3,82
22
4,30
7,94
14,38
3,44
5,72
9,61
3,05
4,82
7,80
2,82
4,31
6,81
2,66
3,99
6,19
2,55
3,75
5,76
2,40
3,45
5,19
2,23
3,12
4,58
2,03
2,75
3,92
1,78
2,30
3,15
2,07
2,82
3,79
23
4,28
7,88
14,19
3,42
5,66
9,46
3,03
4,76
7,67
2,80
4,26
6,70
2,64
3,94
6,08
2,53
3,71
5,56
2,38
3,41
5,09
2,20
3,07
4,48
2,00
2,70
3,82
1,76
2,26
3,05
2,07
2,81
3,77
24
4,26
7,82
14,03
3,40
5,61
9,34
3,01
4,72
7,55
2,78
4,22
6,59
2,62
3,90
5,98
2,51
3,67
5,55
2,36
3,36
4,99
2,18
3,03
4,39
1,98
2,66
3,74
1,73
2,21
2,97
2,06
2,80
3,75
1
2
17
18
50
1
2
25
26
27
28
29
30
60
1
2
3
4
5
6
8
12
24
4,24
7,77
13,88
4,22
7,72
13,74
4,21
7,68
13,61
4,19
7,64
13,50
4,18
7,60
13,39
4,17
7,56
13,29
4,00
7,08
11,97
3,84
6,64
10,83
3,38
5,57
9,22
3,37
5,53
9,12
3,35
5,49
9,02
3,34
5,54
8,93
3,33
5,42
8,85
3,32
5,39
8,77
3,15
4,98
7,76
2,99
4,60
6,91
2,99
4,68
7,45
2,98
4,64
7,36
2,96
4,60
7,27
2,95
4,57
7,18
2,93
4,54
7,12
2,92
4,51
7,05
2,76
4,13
6,17
2,60
3,78
5,42
2,76
4,18
6,49
2,74
4,14
6,41
2,73
4,11
6,33
2,71
4,07
6,25
2,70
4,04
6,19
2,69
4,02
6,12
2,52
3,65
5,31
2,37
3,32
4,62
2,60
3,86
5,89
2,59
3,82
5,80
2,57
3,78
5,73
2,56
3,75
5,66
2,54
3,73
5,59
2,53
3,70
5,53
2,37
3,34
4,76
2,21
3,02
4,10
2,49
3,63
5,46
2,47
3,59
5,38
2,46
3,56
5,31
2,44
3,53
5,24
2,43
3,50
5,18
2,42
3,47
5,12
2,25
3,12
4,37
2,09
2,80
3,74
2,34
3,32
4,91
2,32
3,29
4,83
2,30
3,26
4,76
2,29
3,23
4,69
2,28
3,20
4,65
2,27
3,17
4,58
2,10
2,82
3,87
1,94
2,51
3,27
2,16
2,99
4,31
2,15
2,96
4,24
2,13
2,93
4,17
2,12
2,90
4,11
2,10
2,87
4,05
2,09
2,84
4,00
1,92
2,50
3,31
1,75
2,18
2,74
1,96
2,62
3,66
1,95
2,58
3,59
1,93
2,55
3,52
1,91
2,52
3,46
1,90
2,49
3,41
1,89
2,47
3,36
1,70
2,12
2,76
1,52
1,79
2,13
51
Окончание табл. 4
t
1,71
2,17
2,89
1,69
2,13
2,82
1,67
2,10
2,76
1,65
2,06
2,70
1,64
2,03
2,64
1,62
2,01
2,59
1,39
1,60
1,90
1,03
1,04
1,05
2,06
2,79
3,72
2,06
2,78
3,71
2,05
2,77
3,69
2,05
2,76
3,67
2,05
2,76
3,66
2,04
2,75
3,64
2,00
2,66
3,36
1,96
2,58
3,29
Таблица 5
Таблица Фишера-Иейтса
Значения rкр, найденные для уровня значимости и чисел
степеней свободы = n - 2 в случае парной корреляции
и = n - l - 2, где l - число исключенных величин в случае
частной корреляции
1
2
3
4
5
Двусторонние границы
0,05
0,02
0,01
0,001
0,997
1,000
1,000 1,000
0,950
0,980
0,990 0,999
0,878
0,934
0,959 0,991
0,811
0,882
0,917 0,974
0,754
0,833
0,875 0,951
16
17
18
19
20
Двусторонние границы
0,05
0,02
0,01
0,001
0,468
0,543
0,590
0,708
0,456
0,529
0,575
0,693
0,444
0,516
0,561
0,679
0,433
0,503
0,549
0,665
0,423
0,492
0,537
0,652
6
7
8
9
10
0,707
0,666
0,632
0,602
0,576
0,789
0,750
0,715
0,685
0,658
0,834
0,798
0,765
0,735
0,708
0,925
0,898
0,872
0,847
0,823
25
30
35
40
45
0,381
0,349
0,325
0,304
0,288
0,445
0,409
0,381
0,358
0,338
0,487
0,449
0,418
0,393
0,372
0,597
0,554
0,519
0,490
0,465
11
12
13
14
15
0,553
0,532
0,514
0,497
0,482
0,634
0,612
0,592
0,574
0,558
0,684
0,661
0,641
0,623
0,606
0,801
0,780
0,760
0,742
0,725
50
60
70
80
90
100
0,273
0,250
0,232
0,217
0,205
0,195
0,322
0,295
0,274
0,257
0,242
0,230
0,354
0,325
0,302
0,283
0,267
0,254
0,443
0,408
0,380
0,338
0,338
0,321
0,025
0,01
0,005 0,0005
Односторонние границы
52
0,025
0,01
0,005
0,0005
Односторонние границы
Таблица 6
Т а б л и ц а Z-п р е о б р а з о в а н и я Ф и ш е р а
Z=
r
0,0
1
2
3
4
5
6
7
8
9
0,99
0
0,0000
0,1003
0,2027
0,3095
0,4236
0,5493
0,6932
0,8673
1,0986
1,4722
2,6466
1
0,0101
0,1104
0,2132
0,3205
0,4356
0,5627
0,7089
0,8872
1,1270
1,5275
996
2
0,0200
0,1206
0,2237
0,3316
0,4477
0,5764
0,7250
0,9077
1,1568
1,5890
2,7587
3
0,0300
0,1308
0,2342
0,3428
0,4599
0,5901
0,7414
0,9287
1,1881
1,6584
2,8257
1
2
{ ln (1 + r) - ln (1 - r)}
4
0,0400
0,1409
0,2448
0,3541
0,4722
0,6042
0,7582
0,9505
1,2212
1,7381
2,9031
5
0,0501
0,1511
0,2554
0,3654
0,4847
0,6184
0,7753
0,9730
1,2562
1,8318
2,9945
6
0,0601
0,1614
0,2661
0,3767
0,4973
0,6328
0,7928
0,9962
1,2933
1,9459
3,1063
7
0,0701
0,1717
0,2769
0,3884
0,5101
0,6475
0,8107
1,0203
1,3331
2,0923
3,2504
8
0,0802
0,1820
0,2877
0,4001
0,5230
0,6625
0,8291
1,0454
1,3758
2,2976
3,4534
9
0,0902
0,1923
0,2986
0,4118
0,5361
0,6777
0,8480
1,0714
1,4219
2,6467
3,8002
53
Таблица 7
Значение плотности f (t )
1
2
e
t2
2
значение для нормированного
нормального закона распределения f(t) = f(t)
Целые и десятые доли t
0,0
0,1
0,2
0
0,3989
3970
3910
1
0,3989
3965
3902
2
0,3989
3961
3894
3
0,3988
3956
3885
Сотые
4
0,3986
3951
3876
0,3
3814
3802
3790
3778
3765
0,4
0,5
3683
3525
3668
3503
3653
3485
3637
3467
0,6
0,7
3332
3123
3312
3101
3292
3079
0,8
0,9
2897
2661
2874
2631
1,0
1,1
0,2420
2179
1,2
1,3
доли t
5
0,3984
3945
3867
6
0,3982
3939
3857
7
0,3980
3932
3847
8
0,3977
3925
3836
9
0,3973
3918
3825
3752
3739
3726
3712
3697
3621
3448
3605
3429
3589
3410
3572
3391
3555
3372
3538
3352
3271
3-56
3251
3034
3230
3011
3209
2989
3187
2966
3166
2943
3144
2920
2850
2613
2827
2589
2803
2565
2780
2541
2756
2516
2732
2492
2709
2468
2685
2444
0,2396
2155
0,2371
2131
0,2347
2107
0,2323
2083
0,2299
2059
0,2275
2036
0,2251
3012
0,2227
1989
0,2203
1965
1942
1714
1919
1691
1895
1669
1872
1647
1849
1626
1826
1604
1804
1582
1781
1561
1758
1539
1736
1518
1,4
1,5
1497
1295
1476
1276
1456
1257
1435
1238
1415
1219
1394
1200
1374
1182
1354
1163
1334
1145
1315
1127
1,6
1,7
1109
0940
1092
0925
1074
0909
1057
0893
1040
0878
1023
0863
1006
0848
0989
0833
0973
0818
0957
0804
1,8
1,9
0790
0656
0775
0644
0762
0632
0748
0620
0734
0608
0721
0596
0707
0584
0694
0573
0681
0562
0669
0551
54
Окончание табл. 7
Целые и
десятые доли
t
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
Сотые доли t
0
1
2
3
4
5
6
7
8
9
0,0540
0440
0355
0283
0224
0175
0136
0104
0079
0060
0,0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
0,0001
0,0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
0,0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
0,0001
0,0519
0422
0339
0270
0213
0167
0129
0099
0075
0056
0,0042
0031
0022
0016
0012
0008
0006
0004
0003
0002
0,0001
0,0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
0,0040
0030
0022
0016
0011
0008
0005
0004
0003
0002
0,0001
0,0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
0,0039
0029
0021
0015
0011
0008
0005
0004
0003
0002
0,0001
0,0488
0396
0317
0252
0198
0154
0119
0091
0069
0051
0,0038
0028
0020
0015
0010
0007
0005
0004
0002
0002
0,0001
0,478
0387
0310
0246
0194
0151
0116
0088
0067
0050
0,0037
0027
0020
0014
0010
0007
0005
0003
0002
0002
0,0001
0,0568
0379
0303
0241
0189
0147
0113
0086
0065
0048
0,0036
0026
0019
0014
0010
0007
0005
0003
0002
0002
0,0001
0,0459
0371
0297
0235
0184
0143
0110
0084
0063
0047
0,0035
0025
0018
0013
0009
0007
0005
0003
0002
0001
0,0001
0,0449
0363
0290
0229
0180
0139
0107
0081
0061
0046
0,0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
0,0001
55
Таблица 8
Значение функции Пуассона Р( Х m)
e
m!
m
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0
1
2
3
0,9048
0,0905
0,0045
0,0002
0,8187
0,1637
0,0164
0,0011
0,7408
0,2223
0,0333
0,0033
0,6703
0,2681
0,0536
0,0072
0,6065
0,3033
0,0758
0,0126
0,5488
0,3293
0,0988
0,0198
0,4966
0,3476
0,1216
0,0284
0,4493
0,3595
0,1438
0,0383
0,4066
0,3659
0,1547
0,0494
0,3679
0,3679
0,1839
0,0613
4
5
6
7
0,0000
0,0000
0,0000
0,0000
0,0001
0,0000
0,0000
0,0000
0,0003
0,0000
0,0000
0,0000
0,0007
0,0001
0,0000
0,0000
0,0016
0,0002
0,0000
0,0000
0,0030
0,0003
0,0000
0,0000
0,0050
0,0007
0,0001
0,0000
0,0077
0,0012
0,0002
0,0000
0,0111
0,0020
0,0003
0,0000
0,0153
0,0031
0,0005
0,0001
m
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
0
1
2
3
0,1353
0,2707
0.2707
0,1805
0,0498
0,1494
0,2240
0,2240
0,0183
0,0733
0,1465
0,1954
0,0067
0,0337
0,0842
0,1404
0,0025
0,0149
0,0446
0,892
0,0009
0,0064
0,0223
0,0521
0,0003
0,0027
0,0107
-,0286
0,0001
0,0011
0,0050
0,0150
0,0001
0,0005
0,0023
0,0076
4
5
6
7
0,0902
0,0361
0,0120
0,0034
0,1681
0,1008
0,0504
0,0216
0,1954
0,1563
0,1042
0,0595
0,1755
0,1755
0,1462
0,1045
0,1339
0,1606
0,1606
0,1377
0,0912
0,1277
0,1490
0,1490
0,0572
0,0916
0,1221
0,1396
0,0337
0,0607
0,0911
0,1171
0,0189
0,0378
0,0631
0,0901
8
9
10
11
0,0009
0,0002
0,0000
0,0000
0,0081
0,0027
0,0008
0,0002
0,0298
0,0132
0,0053
0,0019
0,0653
0,363
0,0181
0,0082
0,1033
0,0689
0,0413
0,0225
0,1304
0,1014
0,0710
0,0452
0,1396
0,1241
0,0993
0,0722
0,1318
0,1318
0,1186
0,970
0,1126
0,1251
0,1251
0,1137
12
13
14
15
0,0000
0,0000
0,0000
0,0000
0,0001
0,0000
0,0000
0,0000
0,0006
0,0002
0,0001
0,0000
0,0034
0,0013
0,0005
0,0002
0,0113
0,0052
0,0022
0,0009
0,0264
0,0142
0,0071
0,0033
0,0481
0,0296
0,0169
0,0090
0,728
0,0504
0,0324
0,0194
0,0948
0,0729
0,0521
0,0347
16
17
18
19
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0003
0,0001
0,0000
0,0000
0,0015
0,0006
0,0002
0,0001
0,0045
0,0021
0,0009
0,0004
0,0109
0,0058
0,0029
0,0014
0,0217
0,0128
0,0071
0,0037
m
56
Таблица 9
G - распределение
Пяти- и однопроцентное пределы для отношения G наибольшей выборочной дисперсии
к сумме L выборочных дисперсий, полученных из L независимых выборок объемом n.
Первое значение соответствует уровню значимости = 0,05, а второе - = 0,01
1
2
3
4
5
6
7
8
9
10
16
36
144
2
0,998
0,999
0,975
0,995
0,939
0,979
0,906
0,959
0,877
0,937
0,853
0,917
0,838
0,809
0,816
0,882
0,801
0,867
0,788
0,854
0,734
0,795
0,660
0,700
0,518
0,606
0,500
0,500
3
0,967
0,993
0,871
0,942
0,798
0,883
0,746
0,834
0,707
0,903
0,677
0,761
0,653
0,734
0,633
0,711
0,617
0,691
0,603
0,674
0,547
0,606
0,475
0,515
0,403
0,423
0,333
0,333
4
0,906
0,968
0,768
0,864
0,684
0,781
0,629
0,721
0,590
0,676
0,560
0,641
0,537
0,613
0,518
0,590
0,502
0,570
0,488
0,554
0,437
0,488
0,372
0,406
0,309
0,325
0,250
0,250
5
0,841
0,928
0,684
0,789
0,598
0,696
0,544
0,633
0,507
0,588
0,478
0,553
0,456
0,526
0,439
0,504
0,424
0,485
0,412
0,470
0,365
0,409
0,307
0,335
0,251
0,254
0,200
0,200
6
0,781
0,883
0,616
0,722
0,532
0,626
0,480
0,564
0,445
0,520
0,418
0,487
0,398
0,461
0,382
0,440
0,368
0,423
0,357
0,408
0,314
0,353
0,261
0,286
0,212
0,223
0,167
0,167
7
0,727
0,838
0,561
0,664
0,480
0,569
0,431
0,508
0,397
0,466
0,373
0,435
0,354
0,411
0,338
0,391
0,326
0,375
0,315
0,362
0,276
0,311
0,228
0,249
0,183
0,193
0,143
0,143
0,680
0,795
0,516
8
0,438
0,521
0,391
0,463
0,360
0,423
0,336
0,393
0,319
0,370
0,304
0,352
0,293
0,337
0,283
0,325
0,246
0,278
0,202
0,221
0,162
0,170
0,15
0,125
9
0,639
0,754
0,478
0,573
0,403
0,481
0,358
0,425
0,329
0,387
0,307
0,359
0,290
0,338
0,277
0,321
0,266
0,307
0,257
0,295
0,223
0,251
0,182
0,199
0,145
0,152
0,111
0,111
n-1
L
57