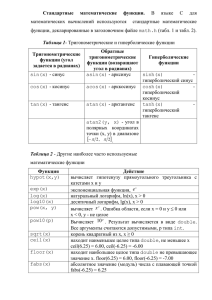
Практикум

Практикум
I. Решение простейших задач:
1. Разработать метод min(a,b) для нахождения минимального из двух чисел. Вычислить с
помощью него значение выражения z=min(3x,2y)+min(x-y,x+y).
Пример.
using System;
namespace Hello
{
class Program
{
static double min(double a, double b)
{
return (a < b) ? a : b;
}
static void Main(string[] args)
{
Console.Write("x=");
double x = double.Parse(Console.ReadLine());
Console.Write("y=");
double y = double.Parse(Console.ReadLine());
double z = min(3 * x, 2 * y) + min(x - y, x + y);
Console.WriteLine("z=" + z);
}
}
}
2.
3.
4.
5.
6.
7.
8.
9.
Разработать метод min(a,b) для нахождения минимального из двух чисел. Вычислить с
помощью него минимальное значение из четырех чисел x, y, z, v.
Разработать метод max(a,b) для нахождения максимального из двух чисел. Вычислить с
помощью него значение выражения z=max(x,2y-x)+max(5x+3y,y).
Разработать метод f(x), который вычисляет значение по следующей формуле: f(x)=x3-sin
x. Определить, в какой из точек а или b, функция принимает наибольшее значение.
Разработать метод f(x), который вычисляет значение по следующей формуле:
f(x)=cos(2x)+sin(x-3). Определить, в какой из точек а или b, функция принимает
наименьшее значение.
Разработать метод f(x), который возвращает младшую цифру натурального числа x.
Вычислить с помощью него значение выражения z=f(a)+f(b).
Разработать метод f(x), который возвращает вторую справа цифру натурального числа x.
Вычислить с помощью него значение выражения z=f(a)+f(b)-f(c).
Разработать метод f(n), который для заданного натурального числа n находит значение
6 +6
13 + 13
21 + 21
+
+
n + n . Вычислить с помощью него значение выражения
.
2
2
2
Разработать метод f(n, x), которая для заданного натурального числа n и вещественного х
находит значение выражения
xn
n . Вычислить с помощью данного метода значение
x2 x4 x6
выражения
.
+
+
2
4
6
10. Разработать метод f(x), который нечетное число заменяет на 0, а четное число уменьшает
в два раза. Продемонстрировать работу данного метода на примере.
1
11. Разработать метод f(x), который число, кратное 5, уменьшает в 5 раз, а остальные числа
увеличивает на 1. Продемонстрировать работу данного метода на примере.
12. Разработать метод f(x), который в двузначном числе меняет цифры местами, а остальные
числа оставляет без изменения. Продемонстрировать работу данного метода на примере.
13. Разработать метод f(x), который в трехзначном числе меняет местами первую с
последней цифрой, а остальные числа оставляет без изменения. Продемонстрировать
работу данного метода на примере.
14. Разработать метод f(a, b), который по катетам a и
b вычисляет гипотенузу. С помощью данного метода
найти периметр фигуры ABCD по заданным сторонам
AB, AC и DC.
15. Разработать метод f(x, y, z), который по длинам сторон
треугольника x, y, z вычисляет его площадь. С помощью
данного метода по заданным вещественным числам a, b,
c, d, e, f, g найти площадь пятиугольника, изображенного
на рисунке.
16. Разработать метод f(x1, y1, x2, y2), который вычисляет длину отрезка по координатам
вершин (x1, y1) и (x2, y2), и метод d(a, b, c), который вычисляет периметр треугольника по
длинам сторон a, b, c. С помощью данных методов найти периметр треугольника,
заданного координатами своих вершин.
17. Разработать метод f(x1, y1, x2, y2), который вычисляет длину отрезка по координатам
вершин (x1, y1) и (x2, y2), и метод max(a, b), который вычисляет максимальное из чисел a,
b. С помощью данных методов определить, какая из трех точек на плоскости наиболее
удалена от начала координат.
18. Разработать метод f(x1, y1, x2, y2), который вычисляет длину отрезка по координатам
вершин (x1, y1) и (x2, y2), и метод min(a, b), который вычисляет минимальное из чисел a,
b. С помощью данных методов найти две из трех заданных точек на плоскости,
расстояние между которыми минимально.
19. Разработать метод f(x1, y1, x2, y2), который вычисляет длину отрезка по координатам
вершин (x1, y1) и (x2, y2), и метод t(a, b, c), который проверяет, существует ли
треугольник с длинами сторон a, b, c. С помощью данных методов проверить, можно ли
построить треугольник по трем заданным точкам на плоскости.
20. Разработать метод f(x1, y1, x2, y2), который вычисляет длину отрезка по координатам
вершин (x1, y1) и (x2, y2), и метод t(a, b, c), который проверяет, существует ли
треугольник с длинами сторон a, b, c. С помощью данных методов проверить, сколько
различных треугольников можно построить по четырем заданным точкам на плоскости.
II. Постройте таблицу значений функции y=f(x) для х[a, b] с шагом h.
Замечание. Для решения задачи использовать вспомогательный метод.
1

( 0.1 + x)2 , если x  0.9;

1. y = 0.2x + 0.1, если0  х < 0.9;
 x 2 + 0.2, если x < 0


Пример:
using System;
namespace Hello
{
class Program
{
2
static double f (double x)
{
double y;
if (x >= 0.9) y = 1 / Math.Pow(1 + x, 2);
else if (x >= 0) y = 0.2 * x + 0.1;
else y = x * x + 0.2;
return y;
}
static void Main(string[] args)
{
Console.Write("a=");
double a = double.Parse(Console.ReadLine());
Console.Write("b=");
double b = double.Parse(Console.ReadLine());
Console.Write("h=");
double h = double.Parse(Console.ReadLine());
for (double i = a; i <= b; i += h)
Console.WriteLine("f({0:f2})={1:f4}", i, f(i));
}
}
}
sin (x), если х  3;

 x2 1
2. y  
, если 3  x  9;
2
 x 5
 2
2
 x  1  x  5, если x  9.
0 , если х  a;
 x-a

, если x  a;
3. y  
x

a

1, если x  a.
 x 3  0.1, если х  0.1;

4. y  0.2 x  0.1, если 0.1  x  0.2;
 3
 x  0.1, если x  0.2.
a  b, если x 2  5 x  0;

5. y  a  b, если 0  (x 2  5 x)  10;
ab, если x 2  5 x  10.

 x 2 , если x 2  2 x  1  2;

 1
6. y   2 , если 2  x 2  2 x  1  3;
 x 1
0, если x 2  2 x  1  3.
 4 , если x  0;

7. y  x 2  3 x  4, если 0  x  1;
2, если х  1.

 x 2  1, если х  1;

8. y  2 x  1, если 1  x  2;
 5
 x  1, если х  2.






3


 x 2  1 2 , если x  1;

 1
9. y  
, если x  1;
2


1

x

0, если х  1.

 x 2 , если (x  2 )  1;

 1
10. y  
, если 1  (x  2 )  10;
x  2
x  2, если (x  2 )  10;
 x 2  5, если x  5;

11. y  0 , если 5  x  20;
1, если x  20.

0, если x  0;

12. y   x 2  1, если x  0 и x  1;
1, если x  1.


1, если x  1 или x  1;

 -1
13. y  
, если х  0 и x  1;
1

x

 1
1  x , если х  0 и х  1.
1, если (x-1 )  1;

15. y  0, если (x-1 )  1;
- 1, если (x-1 )  1.

0.2 x 2  x  0.1, если x  0;
 2
 x
, если x  0 и x  0.1;
14. y  
 x  0. 1
0, если x  0.1.

a  bx, если x  93;

17. y  b - ac, если 93  х  120;
abx, если х  120.

 x 2  0.3, если y  3;

18. y  0, если 3  х  5;
 x 2  1, если х  5.

 5 x 2  5 , если x  2;


x
19. y  
, если 2  х  10;
2
5
x

5

0, если х  10.



sin x , если x  2 ;

π

20. y  cosx , если  x  π;
2

0, если х  π.


 x, если x  0;

16. y  0 , если -1  x  0;
 x 2 , если x  -1.

III. Перегрузите метод f из предыдущего раздела так, чтобы его сигнатура (заголовок)
соответствовала виду static void f (double x, out double y). Продемонстрируйте работу
перегруженных методов.
4