Примеры решения задач Изучить масштабы – численный
реклама
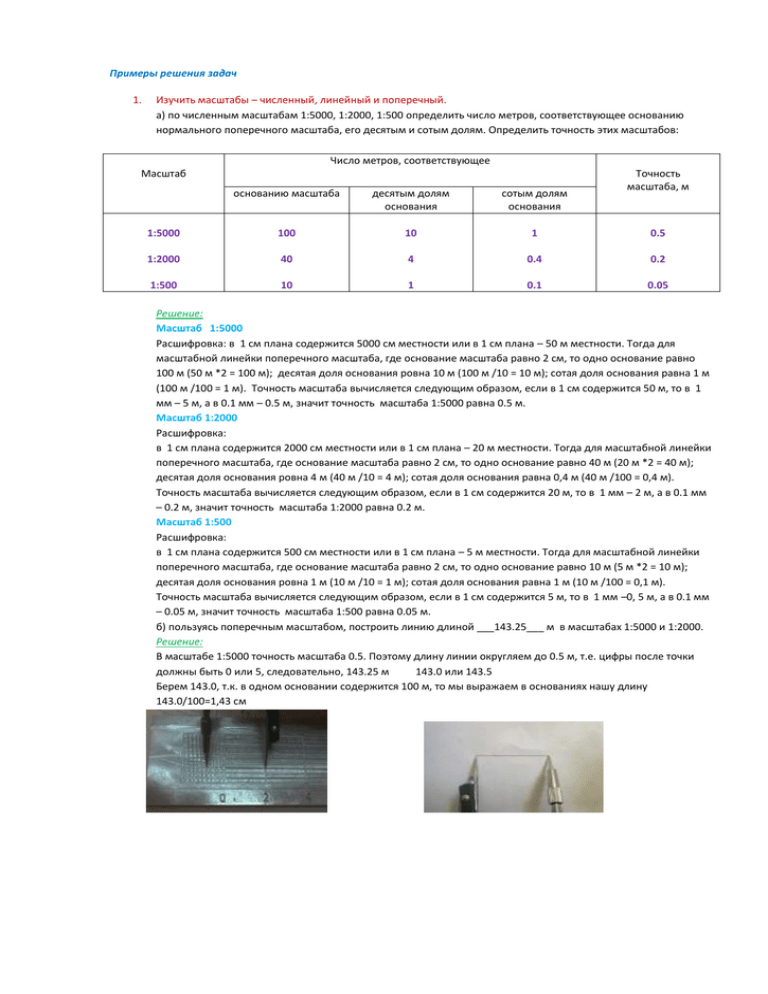
Примеры решения задач 1. Изучить масштабы – численный, линейный и поперечный. а) по численным масштабам 1:5000, 1:2000, 1:500 определить число метров, соответствующее основанию нормального поперечного масштаба, его десятым и сотым долям. Определить точность этих масштабов: Число метров, соответствующее Масштаб Точность масштаба, м основанию масштаба десятым долям основания сотым долям основания 1:5000 100 10 1 0.5 1:2000 40 4 0.4 0.2 1:500 10 1 0.1 0.05 Решение: Масштаб 1:5000 Расшифровка: в 1 см плана содержится 5000 см местности или в 1 см плана – 50 м местности. Тогда для масштабной линейки поперечного масштаба, где основание масштаба равно 2 см, то одно основание равно 100 м (50 м *2 = 100 м); десятая доля основания ровна 10 м (100 м /10 = 10 м); сотая доля основания равна 1 м (100 м /100 = 1 м). Точность масштаба вычисляется следующим образом, если в 1 см содержится 50 м, то в 1 мм – 5 м, а в 0.1 мм – 0.5 м, значит точность масштаба 1:5000 равна 0.5 м. Масштаб 1:2000 Расшифровка: в 1 см плана содержится 2000 см местности или в 1 см плана – 20 м местности. Тогда для масштабной линейки поперечного масштаба, где основание масштаба равно 2 см, то одно основание равно 40 м (20 м *2 = 40 м); десятая доля основания ровна 4 м (40 м /10 = 4 м); сотая доля основания равна 0,4 м (40 м /100 = 0,4 м). Точность масштаба вычисляется следующим образом, если в 1 см содержится 20 м, то в 1 мм – 2 м, а в 0.1 мм – 0.2 м, значит точность масштаба 1:2000 равна 0.2 м. Масштаб 1:500 Расшифровка: в 1 см плана содержится 500 см местности или в 1 см плана – 5 м местности. Тогда для масштабной линейки поперечного масштаба, где основание масштаба равно 2 см, то одно основание равно 10 м (5 м *2 = 10 м); десятая доля основания ровна 1 м (10 м /10 = 1 м); сотая доля основания равна 1 м (10 м /100 = 0,1 м). Точность масштаба вычисляется следующим образом, если в 1 см содержится 5 м, то в 1 мм –0, 5 м, а в 0.1 мм – 0.05 м, значит точность масштаба 1:500 равна 0.05 м. б) пользуясь поперечным масштабом, построить линию длиной ___143.25___ м в масштабах 1:5000 и 1:2000. Решение: В масштабе 1:5000 точность масштаба 0.5. Поэтому длину линии округляем до 0.5 м, т.е. цифры после точки должны быть 0 или 5, следовательно, 143.25 м 143.0 или 143.5 Берем 143.0, т.к. в одном основании содержится 100 м, то мы выражаем в основаниях нашу длину 143.0/100=1,43 см Решение: В масштабе 1:2000 точность масштаба 0.2. Поэтому длину линии округляем до 0.2 м, т.е. цифры после точки должны быть 0;2;4;6;8 (т.е. цифра кратная 2), следовательно, 143.25 м 143.0 или 143.2 Берем 143.0, т.к. в одном основании содержится 40 м, то мы выражаем в основаниях нашу длину 143.0/40=3,575 см. Строится точно так же, как в предыдущем примере. 2. 3. Изучить условные знаки и научиться читать топографические планы. По топографическому плану масштаба 1:2000: а) определить прямоугольные координаты двух точек с точностью масштаба: Наименование точки Прямоугольные координаты Х Р А 149.3 (79.4 – 66.4) е ш В 146.2 (79.2 – 66.2) е Р Решение: Y 79444.0 66458.0 79356.0 66324.0 Пользуясь координатной сеткой, циркулем и поперечным масштабом, по топографическому плану можно определить прямоугольные координаты точки А, находящейся в квадрате 79.4 – 66.4. Необходимо помнить, что абсциссы возрастают к северу, а ординаты - к востоку. Сначала записывают в метрах абсциссу Хюжной линии сетки нижней (южной) линии квадрата, в котором находятся точка А, т.е. Хюжной линии сетки =79400,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = 1,12 также в метрах с точностью масштаба. Δх = 1,12*40=44,8 м (40 основание масштаба 1:2000). Полученную величину Δх=44,8 м прибавляют к абсциссе нижней (южной) линии квадрата Хюжной линии сетки =79400,0 м и находят абсциссу точки А: ХА = 79400,0 + 44,8 = 79444,8 м. Округляем до точности масштаба, т.е. значение после запятой должны быть кратны 2. Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата Узападной линии сетки =66400,0 м прибавляют длину отрезка Δy =1,44, равную 57,6 м, и получают: YА = 66400,0 + 57,6 = 66457,6 м. Аналогично находят точку В. б) определить длину, прямой и обратный дирекционные углы, прямой и обратный румбы линии: Р Наименование линии Длина линии, м Прямой дирекционный угол Обратный дирекционный угол Прямой румб Обратный румб А-В 166.8 230° 50° ЮЗ: 50° СВ: 50° Решение: Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба. На линейке поперечного масштаба а=4,17 см (4 – основания, 10 – десятых долей, 7 – сотых долей). Данное расстояние 4,17*40=166,8 м (40 – основание масштаба 1:2000). Измеряем прямой дирекционный угол в точке А. Проводим линию параллельную осевому меридиану (х линии сетки) = 230° Проводим линию АВ, как показано на рисунке: в) определить отметки двух точек, лежащих между горизонталями с точностью 0,1 м и уклон линии между горизонталями с точностью 0,001: Наименование точки Отметка первой горизонтали Отметка второй горизонтали Заложение, м Расстояние от первой горизонтали до точки, м Отметка точки, м Уклон C 145 146 12,4 9,2 145,5 0,081 D 155 156 20,4 8,4 145,4 0,049 Решение: Преподаватель нанесет на план точки С и D, например: Смотрим к точкам ближайшие горизонтали: для точки С =145, для точки D=156 и измеряем ближайшие расстояния. Точка С: Отметка точки С на нижней горизонтали H1 = 145 м, отметка точки С на верхней горизонтали H 2 = 146 м (т.е. высота сечения рельефа h = 1 м), заложение d = 0,31*40=12,4 м (40 – основание масштаба 1:2000), расстояние от младшей горизонтали до точки С равно с = 0,23*40=9,2 м. Тогда (с требуемой точностью до 0,1 м) вычисляем отметку Н С точки С по формуле Н С H1 c 9,2 h 145 1 145,5 м. d 12,4 Точка D: Отметка точки D на нижней горизонтали H1 = 155 м, отметка точки D на верхней горизонтали H2 = 156 м (т.е. высота сечения рельефа h = 1 м), заложение d = 0,51*40=20,4 м (40 – основание масштаба 1:2000), расстояние от младшей горизонтали до точки D равно с = 0,21*40=8,4 м . Тогда (с требуемой точностью до 0,1 м) вычисляем отметку Н С точки D по формуле НС c 8,4 H1 h 145 1 145,4 м. d 20,4 Уклон линии местности считается по формуле: u tgν h d Для точки С: 𝑢= 1 12,4 = 0,081 Для точки D: 𝑢= 1 = 0,049 20,4 Задачи для самостоятельного решения 1. Изучить масштабы – численный, линейный и поперечный. а) по численным масштабам 1:5000, 1:2000, 1:500определить число метров, соответствующее основанию нормального поперечного масштаба, его десятым и сотым долям. Определить точность этих масштабов: Число метров, соответствующее Масштаб основанию масштаба десятым долям основания сотым долям основания Точность масштаба, м 1:2000 1:5000 1:200 б) пользуясь поперечным масштабом, построить линию длиной _132,53_ м в масштабах 1:5000 и 1:2000. 2. Изучить условные знаки и научиться читать топографические планы. 3.По топографическому плану масштаба 1:2000: а) определить прямоугольные координаты двух точек с точностью масштаба: Наименование точки Прямоугольные координаты Х Y А 148.7 (79.4 – 66.2) В 149.3 (79.4 – 66.4) б ) б) определить длину, прямой и обратный дирекционные углы, прямой и обратный румбы линии: Наименование линии Длина линии, м Прямой дирекционный угол Обратный дирекционный угол Прямой румб Обратный румб А-В в) определить отметки двух точек, лежащих между горизонталями с точностью 0,1 м и уклон линии между горизонталями с точностью 0,001: Наименование точки C D Отметка первой горизонтали Отметка второй горизонтали Заложение, м Расстояние от первой горизонтали до точки, м Отметка точки, м Уклон
