7131 МНК
реклама
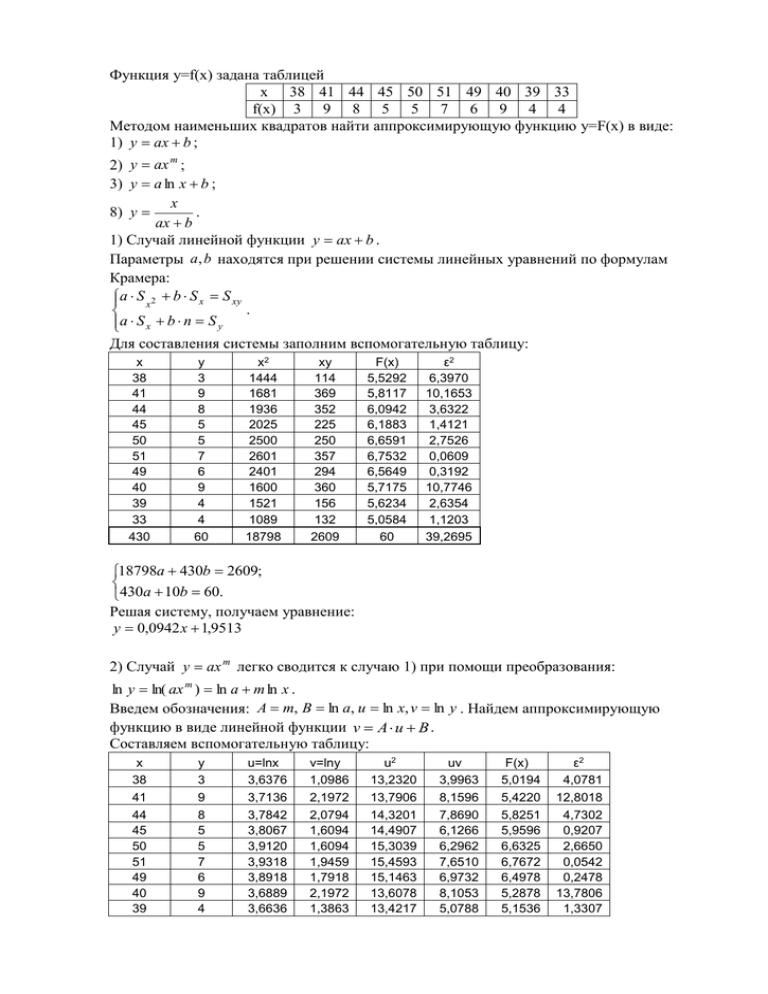
Функция y=f(x) задана таблицей x 38 41 44 45 50 51 49 40 39 33 f(x) 3 9 8 5 5 7 6 9 4 4 Методом наименьших квадратов найти аппроксимирующую функцию y=F(x) в виде: 1) y ax b ; 2) y ax m ; 3) y a ln x b ; x 8) y . ax b 1) Случай линейной функции y ax b . Параметры a, b находятся при решении системы линейных уравнений по формулам Крамера: a S x 2 b S x S xy . a S x b n S y Для составления системы заполним вспомогательную таблицу: x 38 41 44 45 50 51 49 40 39 33 430 y 3 9 8 5 5 7 6 9 4 4 60 x2 1444 1681 1936 2025 2500 2601 2401 1600 1521 1089 18798 xy 114 369 352 225 250 357 294 360 156 132 2609 F(x) 5,5292 5,8117 6,0942 6,1883 6,6591 6,7532 6,5649 5,7175 5,6234 5,0584 60 ε2 6,3970 10,1653 3,6322 1,4121 2,7526 0,0609 0,3192 10,7746 2,6354 1,1203 39,2695 18798a 430b 2609; 430a 10b 60. Решая систему, получаем уравнение: y 0,0942 x 1,9513 2) Случай y ax m легко сводится к случаю 1) при помощи преобразования: ln y ln( ax m ) ln a m ln x . Введем обозначения: A m, B ln a, u ln x, v ln y . Найдем аппроксимирующую функцию в виде линейной функции v A u B . Составляем вспомогательную таблицу: x 38 41 44 45 50 51 49 40 39 y 3 9 8 5 5 7 6 9 4 u=lnx 3,6376 3,7136 3,7842 3,8067 3,9120 3,9318 3,8918 3,6889 3,6636 v=lny 1,0986 2,1972 2,0794 1,6094 1,6094 1,9459 1,7918 2,1972 1,3863 u2 13,2320 13,7906 14,3201 14,4907 15,3039 15,4593 15,1463 13,6078 13,4217 uv 3,9963 8,1596 7,8690 6,1266 6,2962 7,6510 6,9732 8,1053 5,0788 F(x) 5,0194 5,4220 5,8251 5,9596 6,6325 6,7672 6,4978 5,2878 5,1536 ε2 4,0781 12,8018 4,7302 0,9207 2,6650 0,0542 0,2478 13,7806 1,3307 33 430 4 60 3,4965 37,5266 1,3863 17,3016 12,2256 140,9979 4,8472 65,1030 4,3495 56,9144 0,1222 40,7313 А S u 2 В S u S uv А 140,9979 В 37,5266 65,1030 Составляем систему: → А 37,5266 В 10 17,3016 А Su В n Sv В результате решения системы получаем параметры A=1,0154, B=-2,0803. Искомые параметры a, m находятся по формулам: a e B 0,1249, m A 1,0154. F ( x) 0,1249 x1.0154 . 3) Случай y a ln x b легко сводится к случаю 1) при помощи замены u ln x . Найдем аппроксимирующую функцию в виде линейной функции y a u b . Составляем вспомогательную таблицу: x 38 41 44 45 50 51 49 40 39 33 430 u 3,6376 3,7136 3,7842 3,8067 3,9120 3,9318 3,8918 3,6889 3,6636 3,4965 37,5266 y 3 9 8 5 5 7 6 9 4 4 60 u2 13,2320 13,7906 14,3201 14,4907 15,3039 15,4593 15,1463 13,6078 13,4217 12,2256 140,9979 uy 10,91276 33,42215 30,27352 19,03331 19,56012 27,52278 23,35092 33,19992 14,65425 13,98603 225,9157 F(x) 5,497611 5,829342 6,137636 6,235746 6,695717 6,782169 6,607518 5,721542 5,611012 4,881706 60 ε2 6,238061 10,05307 3,468398 1,527068 2,875457 0,04745 0,369079 10,74829 2,59536 0,777405 38,69964 140,9979a 37,5266b 225,9157; Получаем систему: 37,5266a 10b 60. В результате решения системы получаем параметры a 4,37; b 10,38 . F ( x) 4,37 ln x 10,38. x 1 ax b 4) Случай y сводится к случаю 1) при помощи преобразования или ax b y x 1 b a. y x 1 1 Введем обозначения: u , v . Найдем аппроксимирующую функцию в виде x y линейной функции v b u a . Составляем вспомогательную таблицу: x 38 41 44 45 50 51 49 40 39 u 0,0263 0,0244 0,0227 0,0222 0,0200 0,0196 0,0204 0,0250 0,0256 y 3 9 8 5 5 7 6 9 4 v 0,3333 0,1111 0,1250 0,2000 0,2000 0,1429 0,1667 0,1111 0,2500 u2 0,0007 0,0006 0,0005 0,0005 0,0004 0,0004 0,0004 0,0006 0,0007 uv 0,0088 0,0027 0,0028 0,0044 0,0040 0,0028 0,0034 0,0028 0,0064 F(x) 4,6372 5,0937 5,5670 5,7286 6,5678 6,7421 6,3958 4,9397 4,7875 ε2 2,6804 15,2593 5,9196 0,5309 2,4581 0,0665 0,1566 16,4861 0,6202 33 430 0,0303 0,2366 4 60 0,2500 1,8901 0,0009 0,0057 0,0076 0,0457 3,9113 54,3708 0,0079 44,1856 0,0057b 0,2366a 0,0457; 0,2366b 10a 60. 10,0369 -0,0485 В результате решения системы получаем параметры a 0,0485, b 10,0369 . x . F ( x) 0,0485 x 10,0369 Вывод: сравнивая значения суммы квадратов отклонений ε2 видно, что наилучшее приближение МНК даёт логарифмическая функция F ( x) 4,37 ln x 10,38.


