математика 11 кл.

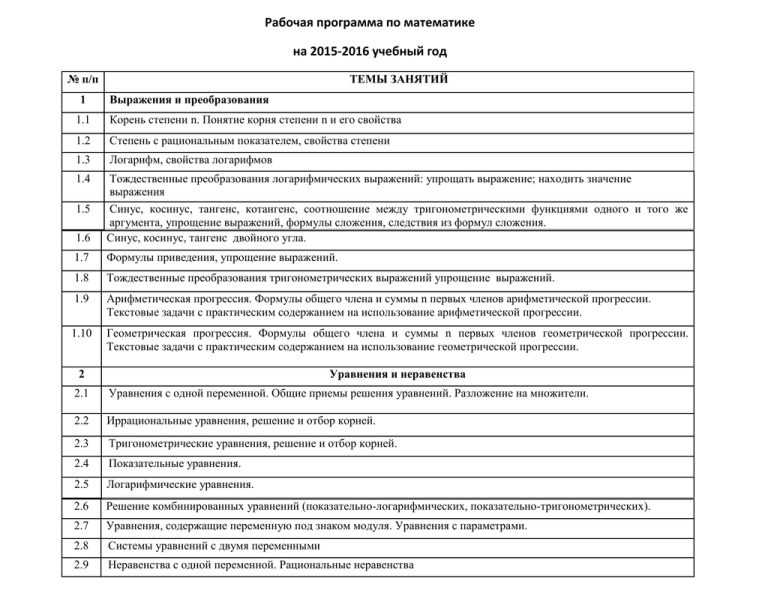
Рабочая программа по математике
на 2015-2016 учебный год
№ п/п
1
ТЕМЫ ЗАНЯТИЙ
Выражения и преобразования
1.1
Корень степени n. Понятие корня степени n и его свойства
1.2
Степень с рациональным показателем, свойства степени
1.3
Логарифм, свойства логарифмов
1.4
1.6
Тождественные преобразования логарифмических выражений: упрощать выражение; находить значение
выражения
Синус, косинус, тангенс, котангенс, соотношение между тригонометрическими функциями одного и того же
аргумента, упрощение выражений, формулы сложения, следствия из формул сложения.
Синус, косинус, тангенс двойного угла.
1.7
Формулы приведения, упрощение выражений.
1.8
Тождественные преобразования тригонометрических выражений упрощение выражений.
1.9
Арифметическая прогрессия. Формулы общего члена и суммы n первых членов арифметической прогрессии.
Текстовые задачи с практическим содержанием на использование арифметической прогрессии.
1.10
Геометрическая прогрессия. Формулы общего члена и суммы n первых членов геометрической прогрессии.
Текстовые задачи с практическим содержанием на использование геометрической прогрессии.
2
Уравнения и неравенства
1.5
2.1
Уравнения с одной переменной. Общие приемы решения уравнений. Разложение на множители.
2.2
Иррациональные уравнения, решение и отбор корней.
2.3
Тригонометрические уравнения, решение и отбор корней.
2.4
Показательные уравнения.
2.5
Логарифмические уравнения.
2.6
Решение комбинированных уравнений (показательно-логарифмических, показательно-тригонометрических).
2.7
Уравнения, содержащие переменную под знаком модуля. Уравнения с параметрами.
2.8
Системы уравнений с двумя переменными
2.9
Неравенства с одной переменной. Рациональные неравенства
2.10
Показательные неравенства.
2.11
Логарифмические неравенства.
2.12
Использование графиков при решении неравенства.
2.13
Неравенства, содержащие переменную под знаком модуля.
2.14
Неравенства с параметром: решать, находить
решения по заданному условию
2.15
Решение комбинированных неравенств: решать, находить решения по заданному условию
2.16
Системы неравенств. Совокупность неравенств. Доказательство неравенств.
Функции
3
3.1
Числовые функции и их свойства. Область определения функции.
3.2
Тригонометрическая функция.
3.3
Показательная функция.
3.4
Логарифмической функция.
3.5
Корень четной степени.
3.6
Экстремумы функции
3.7
Наибольшее (наименьшее) значение функции:
3.8
Производная функции. Геометрический смысл производной: находить угловой коэффициент касательной, тангенс
угла наклона касательной, угол наклона касательной. Физический смысл производной. Таблица производных
Промежутки монотонности.
Построение графиков функций
Решение текстовых задач на нахождение наибольшего (наименьшего) значения величины с помощью производной
3.9
3.10
3.11
4
4.1
4.2
Числа и вычисления
Проценты. Пропорции. Решение текстовых задач
Задачи на движение. Задачи на работу. Задачи на сложные проценты. Задачи на десятичную форму записи числа.
Задачи на концентрацию смеси и сплава.
5
Геометрические фигуры и их свойства. Измерение геометрических величин
5.1
Признаки равенства и подобия треугольников. Решение треугольников (Сумма углов треугольника. Неравенство
треугольника. Теорема Пифагора. Теорема синусов и теорема косинусов). Площадь треугольника. Применять
указанные элементы содержания при решении задач
Многоугольники. Применять указанные элементы содержания при решении задач
Параллелограмм, его виды. Площадь параллелограмма
Трапеция. Средняя линия трапеции. Площадь трапеции
Окружность. Применять указанные элементы содержания при решении задач
Касательная к окружности и ее свойства. Центральный и вписанный углы. Длина окружности. Площадь круга
5.2
Многогранники. Проводить доказательные рассуждения и вычислять значения геометрических величин. Призма.
Пирамида Шар и сфера
6
Элементы комбинаторики, статистики, теории вероятностей
Примечание: программа составлена в соответствии с кодификатором контрольно-измерительных материалов
единого государственного экзамена 2015 г.