Рабочая тетрадь "Индексы"
реклама

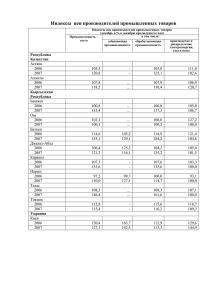
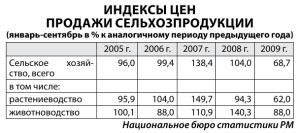
Рабочая тетрадь по предмету «Статистика» «Индексы» Санкт-Петербург 2014 Индекс – относительный показатель, характеризующий изменение сложного экономического явления во времени, пространстве, или по сравнению с эталоном (например, планируемым или нормативным уровнем). Обозначение q Индексируемая величина количество (объем) какого-либо товара цена единицы товара p pq товарооборот (стоимость продукции) себестоимость единицы продукции трудоемкость единицы продукции (затраты рабочего времени на выпуск единицы продукции) Общие затраты времени на выпуск продукции z t T=tq 𝒘 = 𝟏⁄𝒕 количество продукции, вырабатываемое в единицу времени ( телефонов в час ) индивидуальный индекс 𝑖𝑝 , 𝑖𝑞 , 𝑖𝑧 , 𝑖𝑞𝑝 сводный (общий) индекс 𝐼𝑝 , 𝐼𝑞 , 𝐼𝑧 , 𝐼𝑞 1⁄ i I 0 1 символ показателя текущего (отчетного) периода 0 символ показателя предшествующего (базового) периода ∑𝒏 𝑰𝒑𝟏⁄ = ∑𝒊=𝟏 𝒏 𝟎 𝒑𝒊𝟏 𝒒𝒊𝟏 𝒊=𝟏 𝒑𝒊𝟎 𝒒𝒊𝟏 с базовым (0) - индекс цен (p) текущего периода (1) по сравнению Индивидуальные индексы Цены: 𝑖𝑝 = 𝑝1 𝑝0 Физического объема реализации (количества реализованной продукции): 𝑖𝑞 = 𝑞1 𝑞0 Товарооборота: 𝑖𝑝𝑞 = 𝑝1 𝑞1 𝑝0 𝑞0 Связь индивидуальных индексов: 𝑖𝑝𝑞 =𝑖𝑝 𝑖𝑞 Себестоимости: 𝑖𝑧 = 𝑧1 𝑧0 Пример 1. Пусть в текущем периоде продали 𝑞1 = 480 кг. яблок по цене 𝑝1 = 55 руб. за 1 кг., а в базисном периоде продали 𝑞0 = 400 кг. яблок по цене 𝑝0 = 50 руб. за 1 кг. Определите индивидуальный индекс товарооборота, который отражает изменение объема реализации товара в стоимостном выражении. Сделайте вывод. ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ 3 Пример 2. Цена товара А в текущем периоде составляла 30 рублей, а в базисном – 25 рублей. Определить индивидуальный индекс цены. ___________________________________________________________________ ___________________________________________________________________ Пример 3 В I квартале предприятие продало 1200 шт. изделия А по цене 120 руб. за штуку, а во II – 1300 шт. по цене 125 руб. Рассчитать индивидуальные индексы цены, физ. Объема, товарооборота. Показать связь индексов. Что больше повлияло на изменение товарооборота? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ Сводные (агрегатные) индексы Дает характеристику изменения показателя по разнородной совокупности по сравнению с некоторым заданным уровнем. ∑ 𝑥1 𝑓 𝐼𝑥 = ∑ 𝑥0 𝑓 - общая формула агрегатного индекса Где 𝑥1 и 𝑥0 - значения индексируемой величины, соот-но в отчетном и базисном периоде; 𝑓 – вес, или соизмеритель – значения этого показателя должны быть взяты на уровне одного и того же периода – отчетного, или базисного, с тем, чтобы индекс показал изменение только индексируемой величины. Индексы качественных показателей (физ. Объема выпуска, затрат, стоимости) строятся с весами (f) отчетного (1) периода. 𝐼𝑥 = ∑ 𝑥1 𝑓1 ∑ 𝑥0 𝑓1 Индексы количественных показателей (цен, себестоимости, затрат времени) строятся с весами (f) базового (0) периода. 𝐼𝑥 = ∑ 𝑥1 𝑓0 ∑ 𝑥0 𝑓0 ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ 5 Пример 3. Данные о реализации сыров в розничной торговой сети города приведены в таблице ниже: Сорт сыра А Б 1 полугодие Цена за 1 Продано, т кг, руб (𝑞0 ) (𝑝0 ) 80 2,6 72 1,3 2 полугодие Цена за 1 кг, руб (𝑝1 ) Продано, т (𝑞1 ) 83 2,9 76 1,2 В 94 3,8 95 44 Рассчитайте сводные индексы цен, физического объема реализации и товарооборота. Абсолютное изменение товарооборота: всего, в том числе за счет изменения цен и изменения количества проданных товаров. ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ 1 полугодие 2 полугодие Сорт сыра Цена за Прода Цена за 1 кг, руб но, кг 1 кг, (𝑝0 ) (𝑞0 ) руб (𝑝1 ) Прода но, кг (𝑞1 ) А 80 2600 83 2900 Б 72 1300 76 1200 В 94 3800 95 4400 𝒑𝟎 𝒒𝟎 𝒑𝟏 𝒒𝟏 𝒑 𝟎 𝒒𝟏 𝑰𝒑 𝑰𝒒 𝑰𝒑𝒒 Итого: ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ 7 Пример 4. Имеются следующие данные о реализации овощей на рынках города: Август 𝒑𝟏 𝒒𝟏 Изменение цены в августе по сравнению с 𝒑 июлем, % ( 𝟏 ∙ Товарооборот, тыс.руб Товар Июль 𝒑𝟎 𝒒𝟎 𝒑𝟎 Картофель 25 36 𝟏𝟎𝟎%-100%) -9,3 Морковь 12 15 -5,5 Капуста 9 14 -6,7 Рассчитайте сводные индексы цен, физического объема реализации и товарооборота. Абсолютное изменение товарооборота: всего, в том числе за счет изменения цен и изменения количества проданных товаров. Товарооборот , тыс.руб Товар Индивидуаль Товарооборот Изменение ный индекс за август в цены в цен на товары ценах июля, августе по сравнению с 𝒑 𝒑𝟏 𝒒𝟏 июлем, % ( 𝟏 ∙ 𝒊𝒑=𝒑𝟏 𝒑𝟎 𝒒𝟏 𝒑𝟎 = 𝒑𝟎 𝒊𝒑 𝟏𝟎𝟎%-100%) Июль 𝒑 𝟎 𝒒𝟎 Август 𝒑 𝟏 𝒒𝟏 Картофель 25 36 -9,3 Морковь 12 15 -5,5 Капуста 9 14 -6,7 Итого 46 65 ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ Пример 5 Дата торгов 15.11.2013 Эмитент 17.11.2013 Кол-во Рын. Рын. прод. стоимость, стоимость, акций, тыс. руб. руб. шт. 20.11.2013 Кол-во прод. акций, тыс. шт. Рын. стоимост ь, руб. Кол-во прод. акций, тыс. шт. №1 24,3 600 28,1 700 31,5 900 №2 36,2 712 19,7 1234 27.4 1069 №3 38,2 1000 34,5 1285 32,8 880 №4 11220 450 13500 300 14100 200 исходя из приведенных данных, рассчитайте динамику фондового индекса с применением формул: • индекса Пааше; • индекса Лайсперса; • индекса Фишера, сравните полученные результаты и объясните характер различий в полученных ответах. ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ 9 Средние индексы Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. где: i – индивидуальные (индексируемой величины); Средний арифметический индекс физического объема индексы показателя Средний арифметический индекс цен Ласпейреса Средний гармонический индекс объема изучаемого Пааше Средний гармонический индекс цен f и M – веса индекса. Общие индексы могут быть исчислены не только как агрегатные, но и как средние из индивидуальных или групповых. Например, если имеются данные об изменении цен на конкретные товары, то, естественно, из таких индивидуальных индексов могут быть рассчитаны общие (сводные) индексы как средние величины, причем взвешенные Построение цепных и базисных индексов. Индексы с переменной базой сравнения (цепные) получают путем сопоставления индексируемого показателя каждого последующего периода с показателем предшествующего ему периода. Индексы с постоянной базой сравнения (базисные) рассчитывают путем сравнения индексируемого показателя каждого периода с соответствующим показателем одного периода, принятого за базу сравнения. Цепные и базисные агрегатные индексы могут быть исчислены с постоянными и переменными весами. ∑ 𝑥𝑖𝑡 𝑓 • Базисный 𝐼𝑥𝑡⁄ = ∑ 𝑥𝑖0 𝑓 0 ∑ 𝑥𝑖𝑡 𝑓𝑖𝑡 • Веса постоянные 𝐼𝑥𝑡⁄ = ∑ 0 ∑ 𝑝𝑖1 𝑞𝑖1 𝐼𝑝1⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖1 𝑥𝑖0 𝑓𝑖𝑡 ∑ 𝑝𝑖2 𝑞𝑖2 ,𝐼𝑝2⁄ = ∑ 𝑝𝑖0 𝑞𝑖2 0 ∑ 𝑝𝑖3 𝑞𝑖3 ,𝐼𝑝3⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖3 ∑ 𝑝𝑖𝑡 𝑞𝑖𝑡 ,…,𝐼𝑝𝑡⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖𝑡 ∑ 𝑥𝑖𝑡 𝑓𝑖𝑡 • Веса переменные 𝐼𝑥𝑡⁄ = ∑ 0 ∑ 𝑝𝑖1 𝑞𝑖1 𝐼𝑝1⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖0 𝑥𝑖0 𝑓𝑖0 ∑ 𝑝𝑖2 𝑞𝑖2 ,𝐼𝑝2⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖0 ∑ 𝑝𝑖3 𝑞𝑖3 ,𝐼𝑝3⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖0 ∑ 𝑝𝑖𝑡 𝑞𝑖𝑡 ,…,𝐼𝑝𝑡⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖0 ∑ 𝑥𝑖𝑡 𝑓 • Цепной 𝐼𝑥𝑡⁄ 𝑡−1 =∑ 𝑥𝑖,𝑡−1 𝑓 ∑ 𝑥𝑖𝑡 𝑓𝑖0 • Веса постоянные 𝐼𝑥𝑡⁄ 𝑡−1 ∑ 𝑝𝑖1 𝑞𝑖1 𝐼𝑝1⁄ = ∑ 0 𝑝𝑖0 𝑞𝑖0 =∑ ∑ 𝑝𝑖2 𝑞𝑖2 ,𝐼𝑝2⁄ = ∑ 1 𝑝𝑖1 𝑞𝑖0 𝑡−1 ∑ 𝑝𝑖1 𝑞𝑖1 0 𝑝𝑖0 𝑞𝑖1 =∑ 2 𝑝𝑖2 𝑞𝑖0 ∑ 𝑝𝑖𝑡 𝑞𝑖𝑡 ,…,𝐼𝑝𝑡⁄ 𝑡−1 =∑ 𝑝𝑖,𝑡−1 𝑞𝑖0 𝑥𝑖,𝑡−1𝑓𝑖𝑡 ∑ 𝑝𝑖2 𝑞𝑖2 ,𝐼𝑝2⁄ = ∑ 1 ∑ 𝑝𝑖3 𝑞𝑖3 ,𝐼𝑝3⁄ = ∑ ∑ 𝑥𝑖𝑡 𝑓𝑖𝑡 • Веса переменные 𝐼𝑥𝑡⁄ 𝐼𝑝1⁄ = ∑ 𝑥𝑖,𝑡−1 𝑓𝑖0 𝑝𝑖1 𝑞𝑖2 ∑ 𝑝𝑖3 𝑞𝑖3 ,𝐼𝑝3⁄ = ∑ 2 𝑝𝑖2 𝑞𝑖3 ,…,𝐼𝑝𝑡⁄ 𝑡−1 ∑ 𝑝𝑖𝑡 𝑞𝑖𝑡 =∑ 𝑝𝑖,𝑡−1 𝑞𝑖𝑡 11 Пример 6 Товар Продано, шт. Январь Февраль Март Цена за единицу товара, тыс. руб. Январь Февраль Март Косметика 𝒒𝟏 200 𝒒𝟐 210 𝒒𝟑 250 𝒑𝟏 2,0 𝒑𝟐 1,75 𝒑𝟑 1,5 Хоз. товары 300 325 350 0,4 0,35 0,3 • Рассчитайте общие цепные индексы цен с переменными весами, (Изменение цен в феврале по сравнению с январем и в марте по сравнению с февралем.) • Рассчитайте общие цепные индексы физического объема проданных товаров с постоянными весами. (Изменение объема продаж в феврале по сравнению с январем и в марте по сравнению с февралем.) ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ __________________________________________________________________