А.К. ФЕДОСЕЕВ

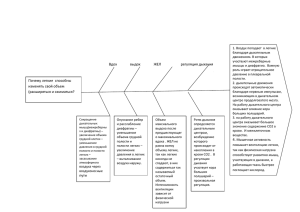
А.К. ФЕДОСЕЕВ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАЗВИТИЯ КАРСТОВЫХ
ПРОЦЕССОВ
В процессе развития карста после образования полости, вследствие
выщелачивания растворимых пород происходит ее рост в латеральном
направлении до некоторого предельного размера, при достижении которого
кровля обрушается и полость заполняется разрушенными вышележащими
(пластичными и сыпучими) породами.
Математическая модель, претендующая на достоверное прогнозирование
формирования карстовых провалов, должна учитывать самые важные, с точки
зрения конечной цели, особенности этапов развития карста.
Для оценки степени воздействия карста на здания и сооружения на данном
этапе исследования нет необходимости в подробном изучении физических
процессов, приводящих к образованию карстовой полости. Достаточно
определить ее начальные размеры и форму, которые не внесут ощутимой
погрешности на конечных стадиях решения задачи.
С учетом анализа, проведенного в [1,2], для начального состояния
растущей карстовой полости подходит расчетная схема, с латеральным размером
полости, выбираемым из условий устойчивости ее кровли. Начальную высоту
полости для геологических условий территории Кунгура можно оценить по
данным работы [3], в которой по результатам изучения Кунгурской пещеры
показано, что отношение горизонтального размера подземной полости к
вертикальному изменяется преимущественно в интервале от 3 до 5.
Очевидно, что при выбранном подходе конечная конфигурация полости
будет существенно отличаться от той геометрической формы, которая
использовалась для нахождения критических размеров полости на предыдущих
этапах работы. Это может привести к существенному отличию напряженнодеформированного состояния (НДС) в породах, перекрывающих карстовую
полость, и как следствие, повлияет на ее критический латеральный размер.
Для определения напряженно-деформированного состояния пород в
окрестности карстовой полости использовалась модель идеальной упругопластичности.
Условием локализации пластических деформаций в области сжатия в
карстующихся породах являлось выполнение равенства:
 max   *  ( р   )[2 р  2  р ( р   c )   c ]
а в области растяжения –
1   р ,
,
(1)
(2)
где  max   1   3  2 – максимальное касательное напряжение,    1   3  2 –
нормальное напряжение,  c – предел прочности на сжатие,  р – предел
прочности на растяжение,  1 ,  3 – главные напряжения, определяемые по
результатам математического моделирования.
Численное решение задачи осуществлялось методом конечных элементов
(МКЭ). Для учета пластического характера деформирования пород использовался
метод секущей матрицы [4].
В качестве условия обрушения пород в окрестности карстовой полости
принимался выход зоны действия растягивающих напряжений [2] или
пластических деформаций на обнажение. Критерием же потери устойчивости
всей потолочины карстовой полости (динамического обрушения) считалось
распространение рассмотренных критериев на всю мощность потолочины.
98
С учетом сказанного для определения критического размера и формы
карстовой полости решалась последовательность задач о напряженнодеформированном состоянии горных пород в окрестности растущей карстовой
полости, учитывающих обрушение пород кровли. Полученная на предыдущем
этапе форма кровли полости становилась начальной на последующем. Если
область
растягивающих
напряжений
и
пластических
деформаций
распространялась на всю потолочину, итерационный процесс завершался.
На каждой итерации отслеживался объем обрушенных из кровли пород.
Несмотря на то, что влияние обрушенных пород на изменение НДС в явном виде
не учитывалось, в случае выполнения неравенства Vпол  k обрVобр (где Vпол –
текущий объем полости, Vобр – объем обрушившихся из кровли пород, k обр –
аналог коэффициента разуплотнения, который, помимо самого разуплотнения,
может учитывать вымывание из полости обрушенных пород), итерационный
процесс останавливался, а полость считалась заполненной.
По результатам математического моделирования выделяется три сценария
обрушения карстовой полости: обрушение в краевой части, высыпание пород в
центральной части и полное обрушение кровли полости.
б)
а)
r
r
Vb
в)
сульфаты
сульфаты
Va
г)
сульфаты
сульфаты
h
- обрушенные породы
- породы, обрушающиеся в краевой части
- породы, перешедшие в пластическое состояние
- обрушающиеся породы надсульфатной толщи
Рис. 1. Обрушение краевой части карстовой полости: достижение полостью
критического размера (а), высыпание пород, перешедших в пластическое
состояние в краевой части (б, в), выход провала на земную поверхность (г)
Необходимым условием реализации того или иного сценария является
«геометрическая» возможность обрушения породы. Так, условием образования
99
карстового провала над краевой частью полости (рис. 1) будет выполнение
неравенства:
Va  Vb  k разVa
(3)
h
 0,
r
где h – высота полости, образующейся на верхней границе сульфатных
отложений, Va – объем высыпающейся в краевой части породы, Vb – объем
полости в краевой части, k раз – коэффициент разуплотнения обрушающейся
породы, r – максимальная ширина области пластических деформаций.
Результаты численных экспериментов показали, что глубина залегания
сульфатов практически не влияет на величину h .
В случае выполнения критерия (3) ширина образующегося карстового
провала (которая, как следует из рис. 1, совпадает с латеральным размером зоны
пластических деформаций) для различных геологических условий определяется
по графикам на рис. 2. Совпадение этих графиков для различных глубин
залегания сульфатов и их выход с ростом мощности карстующихся отложений на
асимптоту объясняет полученный выше вывод об инвариантности h .
r, м
6
Глубина
залегания сульфатов:
10 м
15 м
20 м
25 м
5
4
3
2
0
5
10
15
20
25
mг - hпр , м
Рис. 2. Зависимость максимальной ширины области пластических деформаций
(ширины карстового провала) в краевой части полости от мощности гипсовой
потолочины для различных глубин залегания карстующихся пород
Критерии реализации других сценариев записываются аналогично и дают
подобные же зависимости, что позволяет сделать вывод о независимости их
реализация от глубины залегания карстующихся отложений.
Таким образом, построена модель карстовой полости, учитывающая
изменение ее формы в процессе роста. Модель описывает пластический характер
деформирования карстообразующих пород и обрушение кровли карстовой
100
полости. Введенная модель, помимо определения зависимости предельного
латерального размера карстовой полости от глубины ее начального
формирования, позволила вычленить три возможных сценария образования
карстовых провалов, охватив, таким образом, весь спектр их продольных
размеров. Определенные в первом приближении необходимые «геометрические»
критерии возможности того или иного сценария, позволяют предположить, что их
реализация практически не зависит от глубины залегания карстующихся
отложений. Единообразие полученных критических форм карстовых полостей
позволяет определить начальные условия для проведения в дальнейшем
моделирования образования карстовых провалов методами механики сыпучих
сред. Многовариантные расчеты показали, что для получения более точных
оценок карстоопасности, в дальнейшем необходимо учитывать влияние
обрушившихся из кровли полости пород на изменение НДС в окрестности
полости в процессе ее роста.
СПИСОК ЛИТЕРАТУРЫ
1. Девятков С.Ю. Схема ранжирования карстовых деформаций // Стратегия и
процессы освоения георесурсов: материалы ежегод. науч. сес. ГИ УрО РАН по
результатам НИР в 2005 г. – Пермь, 2006. – С. 116-118.
2. Федосеев А.К. Математическое моделирование устойчивости карстовой
полости // Стратегия и процессы освоения георесурсов: материалы ежегод. науч.
сес. ГИ УрО РАН по результатам НИР в 2007 г. – Пермь, 2008. – С. 102-104.
3. Дорофеев Е.П. Соотношение размеров провальных впадин и карстовых
полостей в сульфатных породах // Вопросы карстоведения. вып. II. – Пермь. 1970.
4. Фадеев А.Б. Метод конечных элементов в геомеханике / А.Б. Фадеев. – М.:
Недра, 1987. – 221 с.
101