конспект открытого урокаx

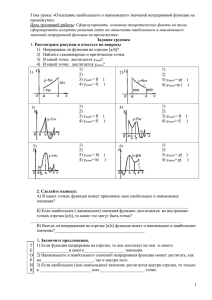
Урок математики в 11 классе
Тема: Наибольшее и наименьшее значение функции на отрезке.
Дидактические цели:
Обучающая:
изучить понятие наибольшего и наименьшего значения функции на отрезке;
познакомиться с алгоритмом вычисления наибольшего и наименьшего значения функции на отрезке;
научить применять изученный алгоритм при решении упражнений;
продолжить работу по формированию умения проводить исследование непрерывной функции y=f(x) на монотонность и экстремумы.
Развивающая:
содействовать развитию у школьников умений использовать научные методы познания (наблюдение, анализ, синтез, сравнение, гипотеза);
создать условия для развития у школьников умений решать задачи, поставленные на уроке.
Воспитывающая:
обеспечить развитие у школьников умения ставить цель и планировать свою деятельность;
содействовать развитию у детей умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
воспитывать чувство уважения между учащимися для максимального раскрытия их способностей.
Учащиеся должны:
усвоить алгоритм вычисления наибольшего и наименьшего значения функции на отрезке;
научиться находить наибольшее и наименьшее значения заданных функций на отрезке;
применять полученные знания при решении упражнений В14 ЕГЭ
Тип урока: комбинированный
Оборудование: доска, карточки, презентация.
этапы
Задания, выполнение которых
приведет к достижению
планируемых результатов
Деятельность учащихся
Организационный момент
Деятельность учителя
Учитель предлагает начать урок
(слайд №1)
Проверка домашнего задания
Объявление темы и цели урока
Целеполагание
Тестовые задания (№9,10,11.12,13)
Из тренировочной работы
Учащиеся называют варианты
ответов.
Учащиеся открывают тетради и
записывают тему урока в тетрадь
Девиз урока
Учитель на доске заносит в таблицу
правильные ответы учащихся в виде
плюса, чтобы наглядно убедиться в
результате выполненной работы.
Если варианты ответов различны,
то учитель предлагает желающим
поделиться своим решением с
остальными.
Учитель объявляет тему урока
(слайд № 2)
- Моя цель ,к которой я буду
стремиться на уроке-это добыть
Учащиеся пытаются поставить цели
и задачи, к которым они будут
стремиться
Повторение теории
1.достаточный признак возрастания
(убывания) функции.
(слайд №3)
2. Какие точки называются
критическими точками функции?
3. Необходимое условие
экстремума функции?
4. Признак максимума (минимума )
Функции.
(Слайд № 4)
Учащиеся называют правила
теоремы, признаки
ваши знания, полученные большим
года назад из укромных уголков
вашей памяти и активизировать их
на работу по повторению темы
«Наименьшее и наибольшее
значение функции»
-И вопрос к вам: « А вам зачем это
нужно?»
-Такие задания есть на ЕГЭ , это
последнее задание в части В-В14
-Еще в 2008 году задания такого
характера были в части С. На
сегодняшний день эти задания
переведены в обязательную часть.
-Разные функции встречаются в этом
задании: функции, выраженные
многочленом, тригонометрические
функции, с экспонентой , с
натуральным логарифмом. Сегодня
на уроке мы научимся находить
наибольшее и наименьшее
значение функции, выраженной
многочленом.
-Для этого нам необходимо
повторить некие постулаты, на
которые мы будем опираться .
Объяснение нового материала
-Вспомним теорему Вейерштрасса
(слайд №16)
Учащиеся под руководством учителя
анализируют, устанавливают
закономерности
-Любая непрерывная функция на
отрезке принимает наибольшее и
наименьшее значение
- Давайте рассмотрим различные
варианты поведения непрерывной
на отрезке функции и попытаемся
определить, в каких точках она
достигает своего наибольшего и
наименьшего значений
(слайд №20)
Анализ всех рассмотренных случаев,
установление закономерности
нахождения наибольшего и
наименьшего значения функции на
отрезке.
-Она на всем отрезке возрастает или
убывает
-наибольшее и наименьшее
значение функция принимает в
точках экстремума.
-Что можно сказать о монотонности
функции на отрезке ( а; в)
Вывод: Если функция на всем
промежутке возрастает (убывает) то
наибольшего или наименьшего
значения она достигает на концах
этого отрезка
-Давайте проанализируем функцию,
имеющую лишь единственную
критическую точку
-В какой точке функция принимает
свое наибольшее ( наименьшее)
значение.
Вывод: Если функция имеет одну
единственную критическую точку и
она является точкой минимума или
максимума, то в этой точке функция
принимает наибольшее или
наименьшее значение.
-А если функция на отрезке имеет
несколько точек экстремума?
Вывод: То своего наибольшего или
наименьшего значения она
достигает либо на концах этого
отрезка, либо в критических точках,
лежащих на данном отрезке.
Составление алгоритма нахождения
наибольшего и наименьшего
значения функции.
-Все это в принципе, легко,
посмотрел на график-вот тебе
наибольшее значение, вот тебе
наименьшее значение. Но дело все
в том, что на экзамене нет графика
функции под рукой. И строить его
нет смысла. Для этого существует
другой способ нахождения
наибольшего и наименьшего
значения функции, и мы с вами
постараемся его составить.
Пример: х𝟒 -2х𝟐 +4 Найти
наибольшее и наименьшее
значение функции на отрезке /о;3/
Учащиеся вместе с учителем
составляют алгоритм
(Слайд № 21)
Учитель объясняет решение у
доски
Закрепление изученного
1.Решение упражнения у доски с
комментированием.
2. Самостоятельная работа по
вариантам.
Пример: х𝟑 -3х𝟐 +3х+2 Найти
наибольшее и наименьшее
значение функции на отрезке /-2;2/
Ответ:нб-4, нм-3
(слайд № 28)
Учащиеся выполняют задание у
доски
Учитель контролирует
Учащиеся самостоятельно решают
задание по вариантам.
Учитель контролирует.
-учащиеся самостоятельно сверяют
полученные ответы с правильными
ответами на доске.
3. Проверка самостоятельной
работы (ответы на доске)
Рефлексия
Учащиеся высказывают свое мнение
Определение домашнего задания
Дома прорешать все задания из
сборника В14, где функция
представлена многочленом.
Записывают домашнее задание
-Каковы ваши главные результаты?
-Что вы поняли? Чему научились?
-Какие чувства испытывали во время
урока?
-Пережили ли чувства радости,
успеха?