Тема 8: Теория выбора в условиях неопределенности Лекция 3
реклама
Тема 8: Теория выбора в условиях неопределенности
Лекция 3.
!
Заметим, что величины денежного эквивалента лотереи и премии за риск зависят от
первоначального богатства индивида!
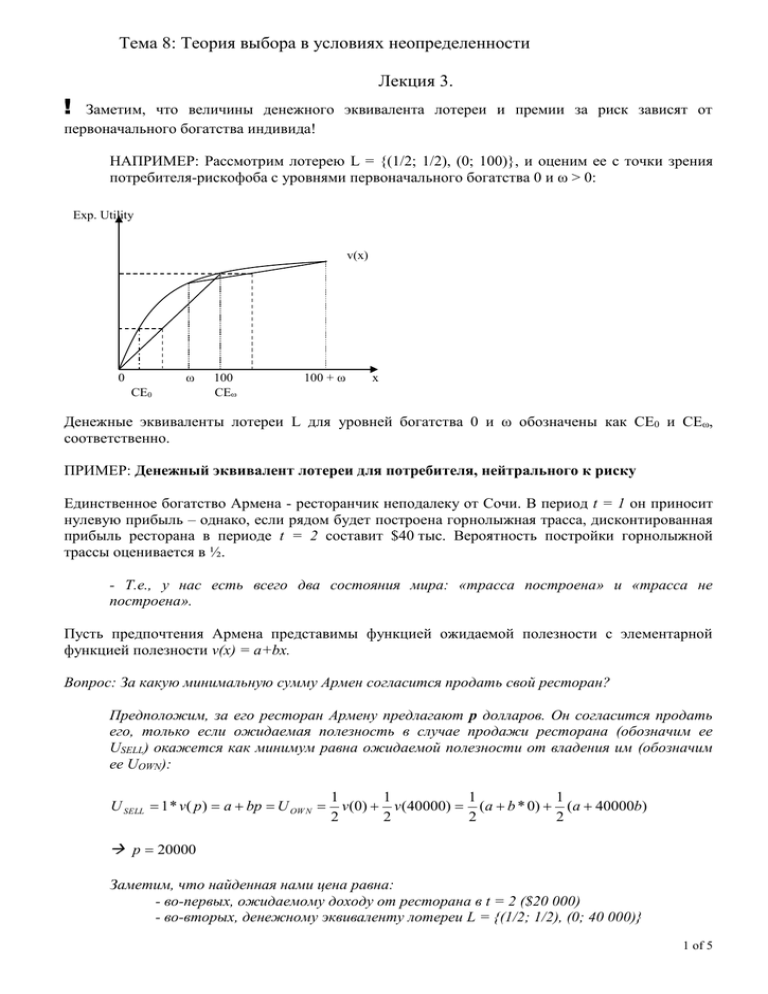
НАПРИМЕР: Рассмотрим лотерею L = {(1/2; 1/2), (0; 100)}, и оценим ее с точки зрения
потребителя-рискофоба с уровнями первоначального богатства 0 и ω > 0:
Exp. Utility
v(x)
Денежный эквивалент лотереи
Будем называть денежным эквивалентом лотереи
Примеры
ω
0
CE0
100
CE
100 + ω
x
Денежные эквиваленты лотереи L для уровней богатства 0 и ω обозначены как CE0 и CEω,
соответственно.
ПРИМЕР: Денежный эквивалент лотереи для потребителя, нейтрального к риску
Единственное богатство Армена - ресторанчик неподалеку от Сочи. В период t = 1 он приносит
нулевую прибыль – однако, если рядом будет построена горнолыжная трасса, дисконтированная
прибыль ресторана в периоде t = 2 составит $40 тыс. Вероятность постройки горнолыжной
трассы оценивается в ½.
- Т.е., у нас есть всего два состояния мира: «трасса построена» и «трасса не
построена».
Пусть предпочтения Армена представимы функцией ожидаемой полезности с элементарной
функцией полезности v(x) = a+bx.
Вопрос: За какую минимальную сумму Армен согласится продать свой ресторан?
Предположим, за его ресторан Армену предлагают p долларов. Он согласится продать
его, только если ожидаемая полезность в случае продажи ресторана (обозначим ее
USELL) окажется как минимум равна ожидаемой полезности от владения им (обозначим
ее UOWN):
U SELL 1 * v( p) a bp U OW N
1
1
1
1
v(0) v(40000) (a b * 0) (a 40000b)
2
2
2
2
p 20000
Заметим, что найденная нами цена равна:
- во-первых, ожидаемому доходу от ресторана в t = 2 ($20 000)
- во-вторых, денежному эквиваленту лотереи L = {(1/2; 1/2), (0; 40 000)}
1 of 5
Примеры использования функции ожидаемой полезности:
ПРИМЕР 1: модель спроса на страховку
- индивид-рискофоб, предпочтения описываются функцией ожидаемой полезности
- первоначальное богатство индивида составляет w
- с вероятностью p (0; 1) происходит несчастный случай
- если он происходит, индивид несет потери L (0; w)
- Страховая компания предлагает индивиду застраховать ущерб:
- стоимость страховки: γ за каждую единицу покрытия (то есть, заплатив γx долларов,
индивид, в случае наступления ущерба, получит возмещение x долларов).
? На какую сумму индивид застрахует свой ущерб?
Индивид стремится выбрать размер покрытия x так, чтобы максимизировать свою ожидаемую
полезность:
max pv( w L x x) (1 p)v( w x)
x
Поскольку индивид – рискофоб, v(.) – строго вогнутая функция. Функция ожидаемой полезности,
таким образом, тоже оказывается строго вогнутой.
Условия Куна-Таккера:
pv' ( w L x x)(1 ) (1 p )v' ( w x) 0, x 0
pv' ( w L x x)(1 ) (1 p )v' ( w x) 0, x 0
При каких условиях индивид будет покупать положительный объем страховки?
В общем случае мы не можем сделать конкретных выводов: ответ зависит от параметров
p, γ и свойств функции v(.), и задача распадается на множество частных случаев.
Рассмотрим один из наиболее важных случаев: случай актуарно справедливой
страховки.
Актуарно справедливая страховка: схема страховки, при которой цена единицы страхового
покрытия равна вероятности наступления страхового случая: γ = p. В этом случае страховая
компания, не имеющая иных издержек, кроме страховых выплат, имела бы нулевую прибыль
при любом объеме продаваемой страховки: (γx – px = 0).
В случае γ = p условия Куна-Таккера принимают следующий вид (заменим γ на p):
pv' ( w L x px)(1 p ) (1 p )v' ( w px) p 0, x 0
p (1 p )v' ( w L x px) v' ( w px) 0, x 0
v' ( w L x px) v' ( w px) 0, x 0
v' ( w L x px) v' ( w px), x 0
pv' ( w L)(1 p ) (1 p )v' ( w) p 0, x 0
p (1 p )v' ( w L) v' ( w) 0, x 0
v' ( w L) v' ( w) 0, x 0
(1)
(2)
Условие (2) выполняться не может, т.к. w – L < w, а v(.) – монотонно возрастающая функция.
Следовательно, x > 0.
Условие (1) выполняется при w L x px w px
xL
ВЫВОД: Если страховка актуарно справедлива, рискофоб застрахует свой ущерб
полностью.
2 of 5
Контингентные блага
Теория ожидаемой полезности – очень удобная конструкция; до тех пор, пока полезность
некоторого потребительского набора (вектора) пропорциональна полезности денег, расходуемых
на покупку этого набора (скалярной величине).
Однако, мы можем описать потребительский выбор в условиях неопределенности и иначе –
пользуясь стандартной концепцией предпочтений, но переопределив само понятие блага.
- Пусть S – мн-во состояний мира (s = 1…S)
- ps – объективная вероятность состояния мира s
Будем называть контингентным благом xis право на получение x единиц i-того физического
блага в состоянии мира s.
Ради упрощения предположим, что физическое благо у нас всего одно – деньги, или
богатство.
! Заметим, что при описании выбора с помощью модели контингентных благ первоначальный
запас также будет привязан к состоянию мира: количество физического блага w, которым мы
первоначально располагаем, превратится в набор контингентных благ (w1, …, wS).
Предпочтения потребителя на множестве наборов контингентных благ мы будем описывать с
помощью обобщенной функции ожидаемой полезности, где элементарная функция полезности
v(.) может зависеть от состояния мира.
Вернемся к ПРИМЕРУ 1 (модели спроса на страховку) и опишем его в терминах
контингентных благ:
- физическое благо: богатство индивида
- состояния мира: {несчастный случай происходит; несчастный случай не происходит} (для
краткости обозначим их как L (loss) и NL (no loss)
контингентные блага: богатство при наступлении несчастного случая (XL); богатство в
отсутствие несчастного случая (XNL)
За первоначальное богатство мы примем богатство индивида, не прибегающего к страховке.
В состоянии мира NL оно составит wNL = w, в состоянии мира L – wL = w – L.
Выведем уравнение бюджетной линии в терминах контингентных благ:
Как и прежде, обозначим объем приобретаемой индивидом страховки за x. Тогда богатство
индивида в состояниях мира L и NL описывается следующей системой уравнений:
X L w L x x
X NL w x
Это и есть уравнение бюджетной линии – правда, оно записано параметрически; и XL, и XNL
выражены через переменную x. Чтобы получить уравнение бюджетной линии в более удобном и
привычном виде, выразим x, например, из второго уравнения системы и подставим в первое.
После некоторых преобразований, мы получим:
3 of 5
XL
1
X NL w L
1
w
Теперь рассмотрим функцию полезности индивида в терминах контингентных благ.
Мы предположили, что предпочтения индивида описываются обобщенной функцией ожидаемой
полезности: Сделаем еще две упрощающих предпосылки:
- пусть v(.) не зависит от состояния мира.
- пусть страховка актуарно справедлива: γ = p.
Отсюда, функция полезности: U(XL, XNL) = pv(XL) + (1 – p)v(XNL) = γv(XL) + (1 – γ)v(XNL)
Запишем задачу потребителя в терминах контингентных благ:
max v( X L ) (1 )v( X NL )
s.t.
XL
1
X NL w L
1
w
ЗАМЕТИМ, что по изначальному предположению, наш индивид – рискофоб, т.е. v(.) строго
вогнута, и значит, U(.) также строго вогнута по каждому аргументу.
Значит, решение может быть найдено методом Лагранжа, причем решение будет единственным:
1
1
L v( X L ) (1 )v( X NL ) w L
w XL
X NL
F.O.C. (для внутренних решений):
dv( X L )
0
L' XL dX
dv( X NL )
dv( X L ) 1
L
L' XNL (1 )
0
dX NL
dX L
dv( X NL )
1
0
L' XNL (1 )
dX NL
L' w L 1 w X 1 X 0
L
NL
1
1
w XL
X NL 0
L' w L
dv( X NL ) dv( X L )
dv( X NL ) dv( X L )
0
(1)
dX
dX
dX L
dX L
NL
NL
w L 1 w X 1 X 0 w L 1 w X 1 X 0 (2)
L
NL
L
NL
! Заметим, что, поскольку v(.) предполагается строго вогнутой, уравнение (1) может выполняться
~
только при XNL = XL = X .
Подставив это в уравнение (2), получим оптимальные значения XNL и XL:
w L
1
1 1
~ 1 ~
~
w X
X 0 X w L
w 1
w L
XL* = XNL* = w – γL – при справедливой страховке рискофоб страхует свой ущерб полностью!
4 of 5
ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ:
XNL
XL = XNL, “certainty line”
U pv( X L ) (1 p)v( X NL )
w
w
tg
1
w – γL
XL
0
w–L
w – γL
α
1
X NL w L
1
w
XL
ЗАМЕЧАНИЕ 1: Пунктирная линия «XL = XNL» или «certainty line» - множество наборов, в
которых потребление не зависит от состояния мира.
ЗАМЕЧАНИЕ 2: Бюджетная линия нарисована с учетом двух не оговоренных заранее, но
довольно естественных ограничений:
- (1): X NL wNL w - если несчастного случая не наступает, ваше богатство при любом
объеме страховки не может быть больше первоначального (ведь невозможно купить
отрицательный объем страхового покрытия?)
- (2): X L w L - нельзя застраховать ущерб на сумму, превышающую этот ущерб
ЗАМЕЧАНИЕ 3: Поскольку U(.) строго вогнута по обеим переменным, ее линии уровня (кривые
безразличия) будут строго выпуклыми.
5 of 5









