Методическая разработка Решение уравнений С
реклама
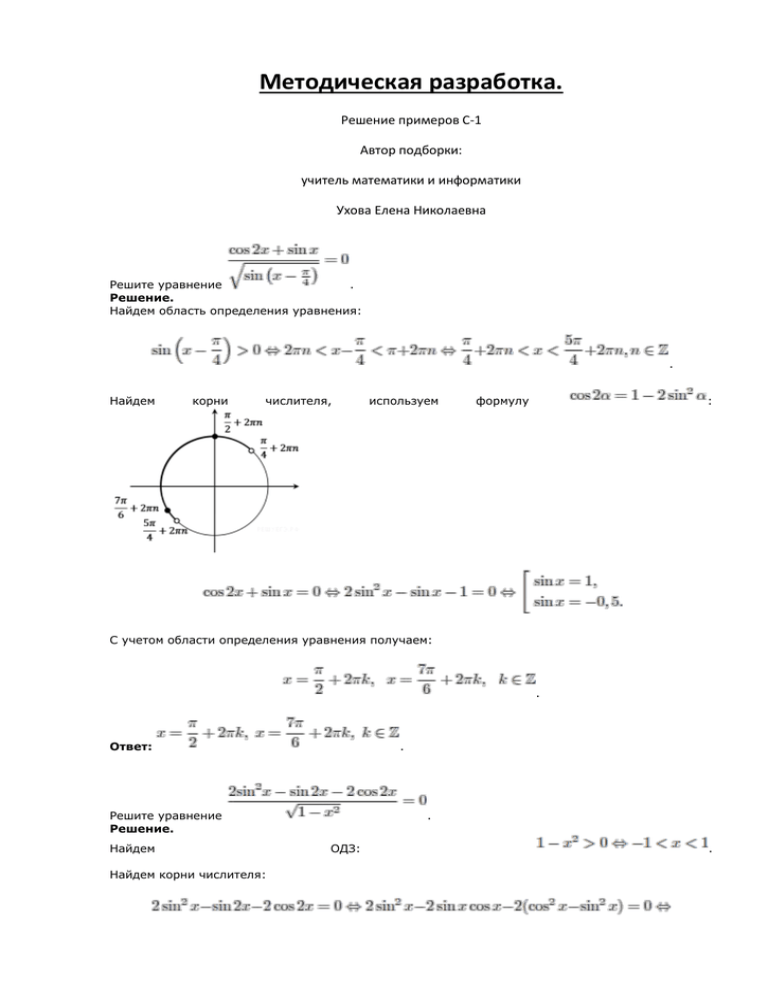
Методическая разработка. Решение примеров С-1 Автор подборки: учитель математики и информатики Ухова Елена Николаевна Решите уравнение . Решение. Найдем область определения уравнения: . Найдем корни числителя, используем формулу : С учетом области определения уравнения получаем: . Ответ: . Решите уравнение Решение. Найдем Найдем корни числителя: . ОДЗ: . Отметим корни на тригонометрической окружности: С учетом ОДЗ Ответ: (см. рис.) получаем: . Решите систему уравнений Решение. Из второго уравнения получаем: или Если , то из первого уравнения то . Уравнение не имеет решений. Если , и из первого уравнения получаем: Ответ: Решите уравнение Решение. . . . . Ответ: . Решите уравнение . Решение. Произведение двух выражений равно нулю, если хотя бы одно из них равно нулю, а другое при этом не теряет смысла: Поскольку , то . Поэтому . Ответ: Решите уравнение Решение. Имеем: Ответ: . . Решите уравнение . Решение. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а другой при этом не теряет смысла. Поэтому данное уравнение равносильно совокупности: Из уравнения получаем ). Решением уравнения либо (что противоречит условию соответствуют две точки единичной окружности, одна из которых лежит в первой четверти (и значит, для нее неравенство выполняется), а другая — в четвертой четверти (для нее неравенство решение уравнения дается формулой ). Теперь осталось выписать решение простейшего тригонометрического уравнения ответ. Ответ: не выполняется, и ; , т. е. , и записать . Решите уравнение . Решение. Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю и не теряет смысла. Поэтому данное уравнение равносильно системе: Решив уравнение . системы как Если квадратное , относительно то Следовательно, и . Если учетом неравенства , находим условие , то . В этом случае с , нужно оставить только ту, для которой . Это точка четвертой четверти, и решение уравнении имеет вид . Решите уравнение Решение. выполняется. системы получаем, что из двух точек единичной окружности, соответствующих решениям уравнения Ответ: либо ; . . Решим уравнение : откуда . Из найденный решений условию (*) удовлетворяет только и . Ответ: , . Решите уравнение Решение. . Решим уравнение : откуда . Из найденных решений условию (*) удовлетворяют только и . Ответ: . Решите систему уравнений Решение. Из неравенства получаем . 1 случай. Пусть второго или уравнения . Если , то получаем 2 случай. Пусть теперь ; если , . Тогда , то откуда или . , и поэтому из первого уравнения получаем: . Учтем, что . Тогда условию удовлетворяет только получаем: . Из . Из всех решений уравнения . При этом и, из второго уравнения . Из всех решений этого уравнения интервалу только . Ответ: этому Значит, принадлежит , . . Решите уравнение Решение. Уравнение равносильно системе . Из неравенства получаем, что . В уравнении сделаем замену и решим уравнение , или . Равенствам и на тригонометрической окружности соответствует четыре точки. Две из них, находящиеся в верхней полуплоскости, не удовлетворяют условию . Получаем решения: . Ответ: , Решите уравнение Решение. Уравнение равносильно системе . . и Решим уравнение: . Тогда или учитывая, что . Последнее уравнение не имеет решений, а из первого, , получаем: Ответ: . . Решите уравнение Решение. Уравнение равносильно системе Уравнение системы приводится . Уравнение к виду , откуда или не имеет решений. Учитывая, что котангенс должен быть отрицательным, Ответ: . получаем: . Решите уравнение Решение. Уравнение равносильно системе . . Уравнение системы приводится к виду Уравнение не имеет , откуда решений. Учитывая, или что . , получаем: . Ответ: . Решите уравнение Решение. Если . , то решений нет. Если , откуда решений. Учитывая, что , то . Если или . Уравнение , из уравнения , то не имеет получаем: . Ответ: ; . Решите уравнение Решение. Левая часть Если . уравнения , то имеет смысл при . , откуда . Если , то , откуда или Уравнение получаем: . не имеет решений. Учитывая, что , из уравнения . Ответ: , Решите уравнение Решение. Левая часть . . уравнения имеет смысл при . Если , то . . Учитывая, что Если , , из уравнения то , откуда получаем: . Ответ: , Дано а) . уравнение Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку Решение. Используем формулу приведения и синуса двойного угла: Тогда или , откуда или б) С помощью единичной окружности отберём корни на отрезке Находим: Ответ: а) б) . Решите уравнение . Укажите его корни, принадлежащие отрезку Решение. Сделаем замену , получим квадратное уравнение являются числа и Уравнение находим искомые корни: корнями которого не имеет решений, а из уравнения или Найдем корни, принадлежащие отрезку , . Решим неравенства: или Соответствующие найденным значениям параметров корни: Ответ: и ; . . Заданному отрезку принадлежат корни и . Решите уравнение Укажите корни, принадлежащие отрезку Решение. Сделаем замену и которого являются числа находим: и получим квадратное Уравнение уравнение не имеет решений, а из уравнения или Найдем корни, принадлежащие отрезку корнями . . , . Отрезку Ответ: принадлежат . только Отрезку корни принадлежат корни: и и . . Дано а) уравнение Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку Решение. а) По формуле приведения и формуле Тогда косинуса двойного или угла: Откуда или б) С помощью единичной окружности отберём корни на отрезке (см. Это числа и рис.). Ответ: а) б) а) Решите уравнение . б) Укажите корни этого уравнения, принадлежащие промежутку Решение. а) Преобразуем уравнение: . Если , то из уравнения следует корней уравнения , что невозможно. Значит, на множестве . Разделим обе части уравнения на : . б) Составим двойное неравенство: , откуда . Следовательно, . Поэтому на данном отрезке получаем единственный корень О т в е т : а) а) ; б) . . Решите уравнение . б) Укажите корни этого уравнения, принадлежащие промежутку Решение. а) Преобразуем уравнение: . . б) Найдем корни, лежащие на заданном отрезке. Составим двойное неравенство: , откуда . Следовательно, или О т в е т : а) , тогда искомые корни ; б) Дано и . Решите Б) Укажите корни уравнения, принадлежащие отрезку Решение. а) Преобразуем уравнение: или . . уравнение А) Получаем: и откуда или уравнение. . б) С помощью числовой окружности отберем Ответ: а) а) корни на отрезке б) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку Решение. а) Разложим левую часть на множители: Уравнение , не имеет корней. Имеем Если , то разделим обе его части на , это невозможно. Это однородное уравнение первой степени, . Получаем: б) Отрезку принадлежат корни О т в е т : а) где а) Решите , б) и (см. рис.) и уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку Решение. а) Преобразуем уравнение и разложим левую часть на множители: Уравнение не имеет корней. Уравнение является однородным тригонометрическим уравнением первой степени. Разделим обе части уравнения на . Получаем: б) Отрезку принадлежит только корень О т в е т : а) , А)Решите , б) уравнение Б) Укажите корни уравнения, принадлежащие отрезку Решение. А) Преобразуем уравнение: Значит, В или первом Первая Б) Отрезку случае во серия Отметим где втором решений решения принадлежат корни входит на и случае где во тригонометрической вторую. окружности. Ответ: А) Б) А) Решите уравнение Б) Укажите корни уравнения, принадлежащие отрезку Решение. А) Преобразуем Первая уравнение, где серия получаем В первом случае решений Значит, или во втором случае входит во Б) Отметим решения на тригонометрической окружности. Отрезку где вторую. принадлежат корни и О т в е т : А) Б) Дано А) уравнение Решите уравнение. Б) Укажите корни уравнения, принадлежащие отрезку Решение. А) Преобразуем уравнение: Получаем: или Отсюда или Б) С помощью числовой окружности отберем корни на отрезке Это числа Ответ: A) Б) Дано уравнение а) . Решите данное уравнение. б) Укажите корни данного уравнения, принадлежащие промежутку Решение. Сведем уравнение к квадратному относительно тангенса: . . Отсюда или . Если . Из , то найденных ; если решений промежутку , то принадлежат числа . О т в е т : а) Дано а) ; б) . уравнение Решите . уравнение. данное б) Укажите корни данного уравнения, принадлежащие промежутку . Решение. . Отсюда или . Если , то . Если . Из найденных решений промежутку и принадлежат числа . О т в е т : а) а) , то ; б) Решите . уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . Решим уравнение: Отберём корни, принадлежащие отрезку . Это числа (см. рис.): . Ответ: A) Б) . ; а) ; . Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . Решим уравнение: Отберём корни, принадлежащие отрезку . Это числа (см. рис.): . Ответ: A) . Б) а) . Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку . . Решение. а) Запишем уравнение в виде Значит, или , откуда , или , , откуда , б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа: Ответ: а) , а) б) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . а) Запишем уравнение в виде . Значит, или , откуда , , или , откуда . б) С помощью числовой окружности отберём корни, принадлежащие отрезку . Получим числа: Ответ: а) , ; а) ; б) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . а) Запишем уравнение в виде Значит, , откуда или . б) С помощью числовой окружности отберём корни, принадлежащие отрезку . Получим . Ответ: а) а) числа: , ; ; б) Решите ; ; ; . уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку . Решение. а) Запишем уравнение в виде Значит, или , откуда , , или или , откуда , . б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку . Получим Ответ: а) а) числа: , Решите ; , , и , ; б) . , и уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде . Значит, или — уравнение не имеет корней, или , , откуда . б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку . Получим Ответ: а) , а) ; б) Решите число . уравнение . . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . а) Запишем уравнение в виде Значит, или , откуда , или или , откуда , б) С помощью числовой окружности отберем корни, принадлежащие отрезку числа: Ответ: а) , , б) Получим а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . а) Запишем уравнение в виде Значит, , откуда . б) С помощью числовой окружности отберём корни, принадлежащие отрезку . Получим . числа: Ответ: а) а) ; ; б) Решите ; ; ; . уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде . Значит, или — уравнение не имеет корней, или или , откуда , . б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку . Получим . число Ответ: а) , а) , ; б) Решите . уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. . а) Запишем уравнение в виде: Значит, или , откуда , , или , откуда , . б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку . Ответ: а) а) Находим , ; Решите , числа ; б) . уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку . . Решение. а) Запишем уравнение в виде: Значит, или , откуда , , или , откуда , . б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа: Ответ: а) а) , ; , Решите ; б) . уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Из данного уравнения получаем: . Значит, или , откуда , или , откуда или б) С помощью числовой окружности отберём корни, принадлежащие отрезку . Получим числа: . Ответ: а) , а) ; , Решите ; б) . уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Из данного уравнения получаем: . Значит, или , откуда , или , откуда б) С помощью числовой окружности отберём корни, принадлежащие отрезку , получим . Ответ: а) а) числа , ; Решите , ; б) . уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде . Значит, или , откуда , , или , откуда , . б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку . Получим Ответ: а) числа: , а) ; Решите , , ; б) , и . и уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. a) Запишем уравнение в виде: . Значит . б) С помощью числовой окружности отберём корни, принадлежащие отрезку Находим числа: Ответ: б) а) . . . . а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде: В результате получим: Значит . б) окружности. Отрезку принадлежат корни Ответ: А) Б) , и , и Отметим решения на тригонометрической