Введение в системы счисления
реклама

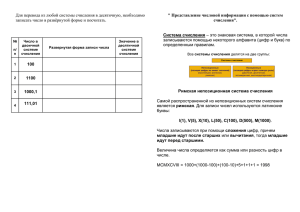
Введение в системы счисления 1. 2. 3. 4. Понятие системы счисления (СС) Непозиционные СС Позиционные СС Пример 10-ой СС Для обмена информацией между людьми используются естественные языки (русский, английский, немецкий и т. д.). В естественных языках для построения слов используются символы, которые отличаются друг от друга написанием. Из символов по некоторым правилам строятся слова и предложения, понятные для человека. Для представления числовой информации (о количестве объектов) то же используются специальные языки, которые описывают символы (в данном случае, цифры) и правила построения чисел из цифр (символов), определяющие порядок записи цифр в числе и операции над числами, то есть правил сложения, вычитания, умножения и т. п. Эти специальные языки называются системами счисления. Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит. Системы счисления (СС) Позиционные СС Непозиционные СС В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), C (100), D (500), M (1000). Значение цифры не зависит от ее положения в числе. Например, в числе ХХХ (30) цифра Х встречается трижды и в каждом случае обозначает одну и ту же величину – число 10, три числа по 10 в сумме дают 30. Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: МСМХСVIII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1 + 1. Число 15 в римской системе – XV = 10 + 5 А число 8 можно представить как: VIII = 5 + 1 + 1 + 1 В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание. Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа. За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m, где ai — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских цифр, и основание, равное 10. Двоичная – две цифры и основание 2. Восьмеричная – восемь цифр и основание 8. Шестнадцатеричная – шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16. Система счисления Десятичная Двоичная Восьмеричная Шестнадцатеричная Основание 10 2 8 16 Алфавит цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А (10), В (11), С (12), D (13), E (14), F (15) Пример записи чисел в 10-ой СС Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления. Рассмотрим в качестве примера десятичное число 555. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. В десятичной системе цифра, находящаяся в крайней справа позиции (разряде), обозначает количество единиц, цифра смещенная на одну позицию влево – количество десятков, еще левее – сотен, затем тысяч и так далее. Число в десятичной позиционной системе счисления записывается в виде суммы числового ряда степеней основания (10), в качестве коэффициентов выступают цифры данного числа. Запись числа 555 в десятичной системе будет выглядеть следующим образом 555 10 = 5 * 102 + 5 * 101 + 5 * 100. Для записи десятичных дробей используются отрицательные значения степеней основания. Например: 555,5510 = 5 * 102 + 5 * 101 + 5 * 100 + 5 *10-1 + 5 *10-2 Индекс 10 у чисел (55510 и 555,5510) обозначает основание системы счисления в которой записано число, в данном примере, это десятичная СС. Десятичная 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Соответствие чисел в различных системах счисления Шестнадцатеричная Восьмеричная 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 10 9 11 А 12 В 13 С 14 D 15 E 16 F 17 Двоичная 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111