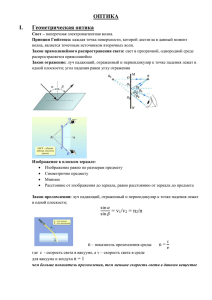
Закон преломления света

Главные этапы в развитии теории света
Первые представления о природе света возникли у древних греков и
египтян, которые в дальнейшем, по мере изобретения и усовершенствования
различных оптических приборов и инструментов развивались и трансформировались.
В конце XVII века на основе многовекового опыта и развития представлений о свете возникли две теории света – корпускулярная (теория истечения) И.Ньютона и волновая теория Х.Гюйгенса.
Согласно первой из них, свет представляет собой поток частиц (корпускул) испускаемых светящимися телами и летящими по прямолинейным траекториям. Движение этих частиц подчинено законам механики.
Согласно волновой теории свет представляет собой упругую волну, распространяющуюся в особой среде – эфире. Эфир заполняет все мировое пространство, пронизывает все тела. Используя сформулированный им принцип
(принцип Гюйгенса) Х.Гюйгенс объяснил все основные законы распространения света.
В течение всего XVIII века корпускулярная теория света занимала господствующее положение в науке (научный авторитет Ньютона), однако острая
борьба между этой и волной теориями света не прекращалась.
В начале XIX века благодаря трудам Т.Юнга и О.Френеля стала складываться последовательно развиваемая система волновой оптики. Несмотря на
признание волновой теории, она обладала целым рядом недостатков. Многие
оптические явления можно было объяснить только в том случае, если световые
волны считать поперечными. Но тогда эфир должен обладать свойствами твердого тела. Более того, оказалось, что скорость света в различных средах различна. Поэтому эфир должен обладать в разных средах различными свойствами.
Накопление экспериментальных данных о связи оптических, электрических и магнитных явлений позволило Д.Максвеллу в 70-х годах XIX века выдвинуть электромагнитную теорию света. В рамках этой теории не удавалось
c
объяснить явление дисперсии света. Согласно этой теории n      . Это
v
соотношение связывает электрические, магнитные и оптические постоянные
вещества. Но, по Максвеллу  и  суть величины постоянные, и, следовательно, показатель преломления вещества не должен зависеть от длины световой
волны, что противоречит опыту. В конце 19 века Лоренц разработал электронную теорию, в рамках которой удалось не только объяснить явление дисперсии
света, но и испускание, и поглощение света.
Несмотря на очевидные успехи теорий Максвелла и Лоренца, они были
несколько противоречивы и, при их применении на практике встречался ряд
трудностей. В частности, эти теории не могли объяснить законов теплового излучения, фотоэффекта, а также многих вопросов взаимодействия света с веществом.
Основные затруднения этих теорий были устранены в квантовой теории, основы которой были заложены М.Планком. А.Эйнштейн в 1905 году создал квантовую теорию света, согласно которой распространение света про-
исходит в виде потока световых квантов - фотонов, энергия которых пропорциональна частоте излучения.
Квантовые представления прекрасно объясняют законы излучения и поглощения света, но в то же время явления интерференции и дифракции света
могут быть объяснены только в рамках волновой теории.
Таким образом, все многообразие изученных свойств и законов распространения света, его взаимодействия с веществом показывает, что свет имеет
сложную природу и обладает корпускулярно-волновым дуализмом.
1.4. Геометрическая оптика
1.1.4. Законы распространения света.
Свет распространяется согласно законам волновой теории. Используя эти
законы, мы можем решать задачи о распространении света, как в однородной
среде, так и через любую оптическую систему. Однако в очень большом круге
вопросов, имеющих важное практическое значение, решение может быть получено гораздо более простым путем с помощью представлений геометрической
оптики. Геометрическая оптика оперирует понятием светового луча, подчиняющегося известным законам преломления и отражения. Понятие светового луча может быть получено из рассмотрения реального светового пучка, из которого при помощи диафрагмы с отверстием мы выделяем узкий пучок света. Чем
меньше диаметр этого отверстия, тем уже выделяемый пучок, и в пределе, переходя к отверстиям сколь угодном малым, мы можем надеяться получить световой луч как геометрическую линию. Однако подобный процесс выделения
сколь угодно узкого пучка невозможен вследствие явления дифракции.
Таким образом, следует иметь в виду, что световой луч есть абстрактное
математическое понятие, а не физический образ. Под световым лучом мы будем понимать линию, направление которой определяет направление распространения световой энергии.
Основные законы распространения света были установлены задолго до
установления природы света. К ним относятся: закон прямолинейного распространения света, законы отражения и преломления света, закон независимости световых пучков.
Закон прямолинейного распространения света – в однородной среде
свет распространяется прямолинейно. ДоказаS
тельством этого закона служит образование тени с
резкими границами от непрозрачных предметов при
освещении их источниками света малых размеров
(рис.1). Закон прямолинейного распространения
Рис. 1. Образование тени за света может считаться прочно установленным на
непрозрачным предметом.
опыте. Он имеет весьма глубокий смысл, ибо само
понятие о прямой линии, по-видимому, возникло из оптических наблюдений.
Закон независимости световых пучков –
2
эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.
Закон отражения света –
отраженный луч лежит в одной плоскости с
падающим лучом и перпендикуляром, проведенном
 
к границе раздела двух сред в точке падения луча.
Угол падения  равен углу отражения  (рис. 2).
Закон преломления света –
луч падающий, луч преломленный и перпендиРис. 2. Отражение света
куляр, проведенный к границе раздела сред в точке
падения луча, лежат в одной плоскости. Отношение синуса угла падения к
синусу угла преломления есть величина постоянная для двух данных сред:
sin 
1.1
 n 21 ,
sin i
где n 21 - относительный показатель преломления второй среды относительно
первой (рис. 3).
Относительный показатель преломления двух сред равен отношению их
абсолютных показателей преломления
n
1.2
n 21  2 .
n1
Абсолютный показатель преломления показывает во сколько раз скорость
света в среде меньше чем в вакууме, т.е.
c
n ,
v
с – скорость света в вакууме, v - скорость света в данной среде.
Учитывая 1.2 закон преломления можно записать в виде:
sin  n 2
1.3
 .
sin i n1
Из симметрии этого выражения вытекает обратимость световых пучков.
Если обратить преломленный луч, заставив его падать на границу раздела под
углом i , то преломленный луч в первой среде будет распространяться вдоль
падающего луча.
Из закона преломления
следует, что при распростране
нии света из оптически менее

плотной среды в более плотную
sin 
1
 n 2  n1  , отношение
sin i
б)
i
а)
и, следовательно, угол падения
i
 больше угла преломления i
(рис. 3а).
Рис. 3. Преломление света: а) при переходе из
оптически менее плотной среды в более плотЕсли же луч света перехоную; б) при переходе из более плотной среды в
дит из оптически более плотной
менее плотную.
3
sin 
 1 и, следовательно,
sin i
  i (рис. 3б). С увеличением угла падения увеличивается и угол преломления, и при некотором значении угла падения  0 угол преломления окажется
равным 90 . Одновременно с этим интенсивность преломленного луча уменьшается, а интенсивность отраженного луча увеличивается и при угле падения
равном  0 интенсивность преломленного луча становится равной нулю, а интенсивность отраженного луча равна интенсивности падающего луча. Поэтому
это явление получило название полного отражения. Угол падения  0 получил
название предельного угла полного отражения. При углах падения больших
 0 весь падающий свет отражается в первую среду. Из закона преломления
света 1.3 можно получить, если учесть, что i  90 и n 2  1 ,
1
1.4
sin 0  .
n
Явление полного отражения нашло широкое практическое применение в
призмах полного отражения (рис.
4). Такие призмы широко применяются в оптических приборах –
биноклях, перископах, телескопах,
а также в рефрактометрах, позволяющих определять показатель
Рис. 4. Ход лучей в призме полного отражения.
преломления вещества.
Явление полного отражения в настоящее время используется в так называемых световодах, которые широко применяются в различных отраслях науки и
техники. Световод представляют собой кварцевую нить, окруженную стеклянным волокном, показатель преломления которого меньше, чем у нити. Свет,
падающий на торец световода, претерпевает на границе раздела нить - волокно
полное отражение и может распространяться только по нити.
среды в менее плотную
 n 2  n1  ,
то отношение
2.1.4. Преломление света на сферической поверхности.
Рассмотрим преломление света на сферической поверхности. Пусть две
прозрачные среды с показателями преломления n1 и n 2 разделены сферической поверхностью радиуса R (рис. 5).
Для построения изображения точки проведем луч, идущий вдоль главной
оптической оси и луч, идущий под малым углом к оптической оси. Будем рассматривать только лучи, составляющие с оптической осью столь малые углы,
что для них синусы и тангенсы можно заменять самими углами, а косинусы
считать равными единице.
4
A
i


S

h

O
R
-d
C
f
S1
Рис. 5. Преломление света на сферической поверхности.
Рассмотрим луч SA, исходящий из точки S, падающий на границу раздела
сред в точке А и пересекающий после преломления главную оптическую ось в
точке S1 . При соблюдении указанного правила знаков закон преломления света
можно записать в виде:
sin() n 2
1.5
 .
sin(i) n1
Заменив синусы углов самими углами, будем иметь:
n 2  i  n1   .
1.6
Из треугольников SСA и S1СA будем иметь      и i     . Подставляя в 1.6, получим:
n1      n 2      .
1.7
Из треугольников SАO, S1AO, AOC с учетом малости углов можно найти
h
h
h
1.8
 ,  ,  .
d
R
f
Подставляя эти значения в 1.7, после преобразования получим:
n 2 n1 n 2  n1
.
1.9
 
f
d
R
Формула 1.9 позволяет определить положение изображения точки, зная
положение точки и радиус кривизны поверхности.
3.1.4. Тонкие линзы. Формула тонкой линзы.
Случай преломления света на одной сферической поверхности сравнительно редок. Большинство реальных систем содержит, по крайней мере, две
преломляющих поверхности или больше двух.
Система сферических поверхностей называется центрированной, если
центры всех поверхностей лежат на одной прямой, которая называется главной
оптической осью.
На практике большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничива5
ющих какой-либо прозрачный хорошо преломляющий материал от окружающего воздуха. Такая система получила название линзы.
Линза называется тонкой, если ее
вершины можно считать совпадающими,
т.е. если толщина линзы мала по сравнению с радиусами кривизны ограничиваюО1
S
О О 2 S
C
щих поверхностей (рис. 6). В дальнейших
расчетах мы будем считать, что точки О 1 и
О 2 сливаются в одну точку О. Все расстоРис. 6. Преломление света в линзе.
яния будем отсчитывать от этой точки.
Точка О получила название оптического центра линзы.
Преломление на первой сферической поверхности создало бы без второй
преломляющей поверхности в сплошном стекле с показателем преломления n 2 ,
изображение на расстоянии OC  a от оптического центра, так что,
n1 n 2 n1  n 2
.
1.10


d a
R1
Для второй сферической поверхности точка С является мнимым источником света. Построение изображения этой точки на второй преломляющей поверхности дает точку S на расстоянии f  OS от оптического центра, так что
n
n n  n1
.
1.11
 2 1 2
a
f
R2
Суммируя выражения 1.10 и 1.11 получим:
 1
1 
1 1
n1      n 2  n 1  

1.12

R
R
d f 
 1
2 
n
Вводя относительный показатель преломления n 21  2 , окончательно
n1
получим общую формулу линзы:
 1
1 1
1 
   n 21  1 

1.13

d f
 R1 R 2 
Общая формула линзы пригодна для любой линзы при произвольном положении источника света. Нужно только принять во внимание знаки d, f, R.
Расстояние от предмета до линзы d считаем положительным для действительного источника (на линзу падает расходящийся пучок лучей). Для мнимого источника это расстояние считается отрицательным (на линзу падает сходящийся
пучок лучей). Расстояние от линзы до изображения f считается положительным
для действительного изображения источника света и отрицательным - для мнимого изображения. Для выпуклой поверхности радиус кривизны считается положительным, для вогнутой поверхности – отрицательным.
6
Если светящаяся точка, лежащая на главной оптической оси, удаляется от
линзы, то изображение ее перемещается. Положение изображения, когда источник удален в бесконечность, носит название фокуса линзы. Другими словами, это есть точка, в которой пересекаются лучи (или их продолжения) падаю-
F
F
а)
б)
Рис. 7. Ход лучей параллельных главной оптической оси.
а) собирающая линза; б) рассеивающая линза.
щие на линзу параллельно главной оптической оси (рис. 7). Расстояние от линзы до фокуса называется фокусным расстоянием F. Для определения фокусного расстояния линзы мы имеем:
 1
1
1 
  n 21  1 

при d  
1.14

F
 R1 R 2 
Из выражения 1.14 следует, что фокусное расстояние линзы зависит
только от относительного показателя преломления материала линзы и радиусов
кривизны ограничивающих поверхностей.
Вводя фокусное расстояние линзы F выражение 1.14, может быть записано в виде:
1 1 1
1.15
 
d f F
1
Величина D  называется оптической силой линзы. Единица измерения
F
1
м  диоптрия.
Линзы с положительной оптической силой называются собирающими, а с
отрицательной – рассеивающими.
Построение изображения предмета в линзах осуществляется с помощью
следующих лучей:
- луча, проходящего через оптический центр линзы и не меняющего
своего направления распространения;
- луча, идущего параллельно главной оптической оси; после преломления в линзе луч (или его продолжение) проходят через фокус;
- луча (или его продолжения), идущего через фокус линзы; после преломления в линзе он идет параллельно главной оптической оси.
7
Для примера на рисунке 8 приведено построение изображения в собираB
B
D
F
А
A
C
O
F
O
C
D
б)
a)
Рис. 8. Построение изображения в линзах.
а) собирающая линза; б) рассеивающая линза.
ющей и рассеивающей линзах.
Отношение линейных размеров изображения и предмета называется линейным увеличением.
H f
1.16
Г  .
h d
4.1.4. Аберрации линз.
В оптике существует понятие об идеальной оптической системе. Принято
считать, что такая система удовлетворяет следующим трем условиям:
- гомоцентрический пучок лучей (т.е. испускаемый точечным источником
света), пройдя через оптическую систему, остается гомоцентрическим, все его
лучи сходятся в одной точке – дают одно точечное изображение);
- изображение предмета по форме остается подобным самому предмету;
- изображение плоскости, перпендикулярной к оптической оси, остается
также перпендикулярно к ней.
Реальные оптические системы и линзы дают изображение с нарушением
гомоцентричности и законов подобия: точка, прямая, плоскость изображаются
в виде пятна, кривой, искаженной плоскости. Изображение искажается, кроме
того, за счет явлений дисперсии и дифракции. Дефекты оптических систем и
линз называют аберрациями.
Сферическая аберрация.
Сферическая аберрация – явление нарушения гомоцентричности лучей,
прошедших через оптическую систему без нарушения симметрии этих лучей.
Пусть, например, пучок лучей параллельных оптической оси падает на линзу
(рис. 9; лучи 1,2,3,4,5.). Согласно условиям идеальной оптической системы лучи такого пучка должны, после преломления в линзе, сойтись в ее фокусе. В
действительности в фокусе сойдутся лишь параксиальные лучи (луч 1 на рис.
9). Лучи падающие ближе к краям линзы (2, 3, 4 и 5) будут иметь большие углы
преломления, чем лучи в центральной зоне линзы. Вследствие этого они схо8
дятся в точках, не совпадающих с фокусом. Следовательно, параллельные лучи,
не дают точечного изображения, т.е. нарушается гомоцентричность пучка лучей.
dr
5
4
r
3
2
1
F
r2

r
r1
Рис. 9. Ход лучей в линзе от источника света,
удаленного в бесконечность.
Мерой сферической аберрации являются: продольная и поперечная сферическая аберрации.
Поперечная сферическая аберрация  - радиус пятна изображения точечного источника света при данной диафрагме, на экране установленном в фокусе
линзы.
Продольная сферическая аберрация – разность расстояний от линзы до
точки схождения крайних лучей при данной диафрагме и фокусным расстоянием dr  r2  F .
Собирающие линзы имеют отрицательную продольную аберрацию, а
рассеивающие – положительную. Поэтому, комбинируя собирающие и рассеивающие линзы можно значительно уменьшить сферическую аберрацию.
Нетрудно видеть, что диафрагмирование, ограничивая ширину светового
пучка, ослабляет сферическую аберрацию.
Одновременно с этим изменяется глубина резкости изображения
r  r1  r2 , где r1 - расстояние до задней точки размытия изображения, а r2 - расстояние до передней точки.
Кома.
Кома – явление аналогичное сферической аберрации для точечного источника света лежащего на некотором расстоянии от оптической оси линзы
(рис. 10). На экране Э, установленном в фокальной плоскости линзы, точка А
изображается в виде пятна эллиптической формы, имеющей неравномерную
9
яркость. Размер пятна увеличивается с увеличением расстояния SS . Это объясняется тем, что от такого источника лучи пересекаются в точке A  лежащей
вне плоскости экрана (рис. 10).
A
S
Э
Астигматизм.
S
А
Рис. 10. Ход лучей в линзе для источника лежащего на некотором расстоянии от оптической
оси.
Астигматизм – аберрация, возникающая из-за неравенства кривизны
поверхностей линзы в различных
плоскостях. Причиной этого может
быть неточность изготовления поверхности линзы или падение на линзу косых лучей от источника не лежащего
на оптической оси линзы.
Рассмотрим случай явления астигматизма при косом падении лучей на
линзу (рис. 11). Лучи от источника S, лежащего вне оптической оси линзы, падают S
на нее под некоторым углом.
Для лучей идущих в горизонтальной плоскости и лучей,
идущих
в
вертикальной
r2
плоскости кривизна поверхности линзы различна. В реr1
зультате точки схождения
лучей падающих в горизонРис. 11. Ход лучей в линзе (сплошная линия лежатальной плоскости не совпащие в вертикальной плоскости, пунктирная линия – в
дут с точкой схождения лугоризонтальной).
чей падающих в вертикальной плоскости.
При установке экрана в этих точках мы увидим изображение точки в виде
отрезка прямой либо вертикального, либо горизонтального. При установке
экрана между этими точками изображение имеет вид эллипса.
Количественно астигматизм характеризуется расстоянием между точками
схождения лучей, падающих в горизонтальной и вертикальной плоскостях. Оно
называется астигматической разностью линзы
dr  r1  r2 ,
где r1 - расстояние от линзы до экрана, при котором четко видны горизонтальные линии, а r2 - расстояние от линзы до экрана, при котором четко видны вертикальные линии.
Астигматизм хорошо наблюдается по изображению миллиметровой сетки, нанесенной на прозрачную пластинку, в косых лучах, проходящих через
пластинку и линзу.
10
Зависимость астигматической разности от угла падения лучей  показана на рисунке 12 в полярных коорди60
натах.
70
80
Астигматизм исправляется путем
подбора радиусов кривизны преломляющих поверхностей и их фокусных
расстояний.
90
Хроматическая аберрация.
Рис.12. Зависимость астигматической
разности от угла падения лучей.
Хроматическая аберрация вызывается дисперсией света проходящего
через линзу. Спектральное разложение света создает окраску изображения, особенно на краях изображения
предмета.
 1
1
1 
  n  1 

 содержит в
F
R
R
 1
2 
себе показатель преломления n. Как известно, показатель преломления различен для световых волн с различной длиной волны. В силу этого точки схождения лучей различного цвета не совпадают, и изображение приобретает размытый характер с цветовой окраской.
Так как разные сорта стекла обладают различной дисперсией, то комбинируя собирающие и рассевающие линзы, изготовленные из различных стекол
можно в значительной степени уменьшить хроматическую аберрацию.
Устранение аберраций возможно лишь путем подбора специально рассчитанных сложных оптических систем. Одновременное исправление всех
аберраций задача крайне сложная, а иногда даже неразрешимая. Поэтому
обычно полностью устраняют лишь те погрешности линз, которые в данном
конкретном случае особенно вредны.
Формула фокусного расстояния линзы
5.1.4. Оптические приборы.
Человеческий глаз по своему устройству является аналогом фотоаппарата. Роль объектива играет совокупность преломляющих сред, состоящая из водянистой влаги, хрусталика и стекловидного тела.
Наводка на различно удаленные предметы (аккомодация) достигается
путем мышечного усилия, изменяющего радиус кривизны (фокусное расстояние) хрусталика. Пределы расстояний, в которых возможна аккомодация, носят
название дальней и ближней точек аккомодации. Для нормального глаза дальняя точка, фиксируемая без усилия, лежит в бесконечности, а ближняя – на расстоянии 25 см от глаза (расстояние наилучшего зрения).
Строго говоря, это не очень совершенная система. В ней ясно выражены
и сферическая аберрация, и астигматизм, и значительная хроматическая абер11
рация. Однако эти недостатки очень мало чувствуются благодаря ряду особенностей глаза.
Сферическая аберрация мало заметна, так как освещенность в пятне рассеивания очень неравномерна и самая светлая, и самая важная для зрительного
ощущения часть пятна очень мала.
Астигматизм наклонных пучков почти незаметен, так как мы бессознательно изображение каждой точки переводит на ось глаза, проходящую через
самую выгодную часть сетчатки. Недостаток поля зрения компенсируется превосходной подвижностью глаза.
Хроматическая аберрация практически незаметна, так как глаз очень чувствителен лишь к сравнительно узкой части спектра.
Человеческий глаз способен раздельно воспринимать две точки только в
том случае, если угол, образованный прямыми, проходящими через эти точки и
оптический центр глаза (угол зрения) больше одной минуты. С уменьшением
расстояния от предмета до глаза угол зрения увеличивается. Однако существует
минимальное расстояние, на котором глаз способен отчетливо видеть предмет –
ближний предел аккомодации d 0 . Для среднего здорового глаза d 0  25 см . Таким образом, угол зрения человеческого глаза ограничен.
Вследствие характера структуры сетчатки, состоящей из отдельных элементов, глаз воспринимает как одну точку, две точки объекта, если они
настолько близки, что обе изображаются на одном элементе сетчатки (колбочке). Таким образом, участок предмета, изображение которого лежит на одном
элементе сетчатки, воспринимается как точка и никакое распознавание деталей
в пределах этого участка невозможно. Величина этого участка определяется углом зрения. Для нормального глаза этот угол зрения составляет 1 .
При рассматривании мелких предметов следует искусственно увеличивать угол зрения, что достигается применением оптических приборов – лупы и
микроскопа.
Собирающая линза с фокусным расстоянием меньше 10 см получила
название лупы.
F
F
б)
а)
Рис. 13. Ход лучей в лупе. а) предмет помещен в фокусе линзы;
б) предмет помещен на расстоянии меньше фокусного.
При работе лупа помещается вплотную к глазу, а предмет в ее фокусе или
на расстоянии немного меньше фокусного. При этом мнимое увеличенное
изображение предмета получается или в бесконечности (рис. 13.а), или на расстоянии наилучшего зрения (рис. 13 б). При обоих способах применения лупы
увеличение, ею даваемое, практически одно и то же и равно
12
d0
,
1.17
F
где d 0 - расстояние наилучшего зрения, F – фокусное расстояние лупы. Как следует из формулы 1.17, увеличение лупы зависит от фокусного расстояния линзы, но оно в свою очередь зависит от радиусов кривизны поверхности. Поэтому
линза с малым фокусным расстоянием имеет небольшие размеры и пользоваться такой лупой неудобно. Обычно применяемые лупы дают увеличение от 2,5
до 25.
Для получения больших увеличений применяют микроскоп, представляющий собой комбинацию двух оптических систем – объектива и окуляра, - разделенных значительным расстоянием. Ход лучей в микроскопе показан на рисунке 14.
Предмет АВ помещается между фокусом и двойным фокусом объектива,
который дает действительное увеличенное изображение предмета MN . Это
изображение, в свою очередь, является предметом по отношению к окуляру,
который располагается так, что изображение предмета MN оказывается между
фокусом и линзой. При этом мнимое изображение предмета, даваемое окуляром CD , получается на расстоянии наилучшего зрения от глаза наблюдателя.
Г
C
N
B
А
M
D
Рис. 14. Ход лучей в микроскопе. AB – предмет; MN- изображение, даваемое объективом; CD – изображение предмета в окуляре.
Линейное увеличение микроскопа равно произведению увеличений окуляра и объектива Г  Гоб  Гок .
Обычно увеличение микроскопа связывают с фокусными расстояниями
окуляра и объектива, расстоянием наилучшего зрения и длиной тубуса L, приблизительно равной расстоянию между задним фокусом объектива и передним
фокусом окуляра. Для простоты рассуждений можно считать, что
f
L
f
d
f1  L, d1  F1 и d 2  F2
и значит Г1 об   1  , Г 2 ок   2  0 .
d1 F1
d 2 F2
Тогда
Ld
1.18
Г 0 .
FF
1 2
13
Увеличение микроскопа не может быть сколь угодно большим, и его значение не превышает 2000. Это связано с ограниченной разрешающей способностью микроскопа, обусловленной дифракционными явлениями, так как изображение предмета есть результат дифракции и интерференции света, рассеянного
предметом.
Это интересно. Из полученного выражения следует, что увеличение микроскопа
можно сделать сколь угодно большим, если уменьшить фокусные расстояния окуляра и объектива. Однако многочисленные попытки осуществить это на практике не привели к успеху.
Тогда владелец оптической мастерской Карл Цейс пригласил молодого физика, выпускника
университета Аббе. Аббе прежде всего попытался разобраться с теорией вопроса и показал,
что волновая природа света накладывает ограничения на увеличение микроскопа.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Задачи к зачету
Линза, расположенная между предметом и экраном дает, дает на экране увеличенное изображение предмета. Когда линзу передвинули на 40 см ближе к
экрану, на нем появилось четкое уменьшенное изображение предмета.
Определить фокусное расстояние линзы, если расстояние между предметом
и экраном равно 80 см.
Каково наименьшее возможно расстояние между предметом и его действительным изображением, создаваемым собирающей линзой с фокусным расстоянием 12 см?
Доказать, что оптическая сила системы сложенных вместе тонких линз равна алгебраической сумме оптических сил каждой из этих линз.
У линзы находящейся в воздухе фокусное расстояние равно 5 см, а погруженной в раствор сахара 35 см. Определить показатель преломления раствора сахара.
Определить оптическую силу выпукло-вогнутой линзы с радиусами кривизны 1 м и 40 см, изготовленной из стекла с показателем преломления 1,5.
Определить радиусы кривизны выпукло-вогнутой линзы, если известно, что
один из них в три раза больше другого, а оптическая сила линза равна
8 дптр.
Два плоских зеркала образуют двугранный угол   179 . На расстоянии
 10 см от линии соприкосновения зеркал и на одинаковом расстоянии от
каждого зеркала находится точечный источник света. Определить расстояние между мнимыми изображениями источника в зеркалах.
Пучок параллельных лучей падает на толстую стеклянную пластинку под
углом 60 , и, преломляясь, переходит в стекло. Ширина пучка в воздухе
равна 10 см. Определить ширину пучка в стекле, если показатель преломления стекла равен 1,5.
Луч света переходит из среды с показателем преломления n 1 в среду с показателем n 2 . Показать, что если отраженный и преломленный лучи взаимно
n
перпендикулярны, то выполняется условие tg  2 , где  - угол падения
n1
луча.
14
10. Отношение радиусов кривизны поверхностей линзы равно 2. Определить
радиус кривизны выпуклой поверхности линзы, если оптическая сила линзы
равна 10 дптр.
11. Определить радиус кривизны выпуклой поверхности линзы, если при отношении радиусов кривизны поверхностей линзы, равном 3, ее оптическая сила равна – 8 дптр.
12. Линза изготовлена из стекла, показатель преломления которого для красных
лучей 1,50, а для фиолетовых 1,52. Радиусы кривизны поверхностей линзы
одинаковы и равны 1 м. Определить разность фокусных расстояний линзы
для красных и фиолетовых лучей.
13. Фокусное расстояние собирающей линзы в воздухе равно 10 см. Определить чему оно будет равно в воде, если показатель преломления стекла равен
1,5, а воды 1,33.
14. Человек без очков читает книгу, располагая ее на расстоянии 12,5 см от глаза. Какой оптической силы очки ему надо носить?
2.2. Интерференция света
1.2.4. Интерференция света. Условия образования интерференционного
максимума и минимума.
Для описания световой волны можно воспользоваться уравнением гармонических колебаний x  Acos  t  0  , где под x понимают напряженность
электрического E или магнитного H полей волны. И тогда интерференцию
света можно объяснить рассматривая сложение колебаний.
Ранее мы показали, что при сложении двух гармонических колебаний одного периода происходящих по одному направлению x1  A1 cos  t  1  и
x 2  A2 cos  t  2  , получается вновь гармоническое колебание того же периода x  Acos  t   , амплитуда А которого определяется из соотношения
A 2  A12  A 22  2A1A 2 cos  2  1 
2.1
Из данного выражения следует, что квадрат амплитуды результирующего
колебания не равняется сумме квадратов амплитуд складываемых колебаний,
т.е. интенсивность результирующего колебания не равна сумме интенсивностей
складываемых колебаний. Так как интенсивность волны I A2 , то можно написать
2.2
I  I1  I2  2 I1  I2 cos  2  1  .
Отсюда следует, что в тех точках пространства где cos  2  1   0
I  I1  I 2 , а там где cos  2  1   0 I  I1  I 2 . В частности, при I1  I 2 будем
иметь I  4I1 при  2  1   0 и I  0 при  2  1    .
Следовательно, при наложении двух колебаний происходит пространственное перераспределение энергии колебаний, в результате чего в одних точ15
ках возникают максимумы, а в других минимумы колебаний. Это явление и
называют интерференцией света.
Однако нужно иметь в виду тот факт, что полученный результат будет
иметь место только в том случае, если разность фаз складываемых колебаний
 2  1  не меняется с течением времени. Такие волны называются когерентными.
Этому условию удовлетворяют так называемые монохроматические волны – не ограниченные в пространстве и во времени волны одной строго определенной частоты и постоянной амплитуды.
Если же разность фаз складываемых колебаний беспорядочно меняется
во времени, то интенсивность результирующего колебания будет равна сумме
интенсивностей складываемых колебаний, так как в этом случае среднее значе

ние разности фаз  2  1   и, следовательно, cos  0 и I  I1  I 2 . Колеба2
2
ния в этом случае называются не когерентными. Поэтому мы не наблюдаем интерференции света от двух независимых источников света (например, от двух
электрических лампочек).
Объяснить это можно следующим образом. Процесс излучения света
атомом конечен и длится очень короткое время ( 108 c ). Через некоторое время
атом может снова возбудиться и начать испускать световые волны, но уже с
другой начальной фазой. В двух независимых источниках света атомы излучают свет независимо друг от друга и в результате этого волны, излучаемые ими,
не будут являться когерентными.
Поэтому для наблюдения интерференции света применяют метод разделения волны излучаемой одним источником, на две части, которые после прохождения различных оптических путей накладываются друг на друга.
Пусть в точке О, где происходит разделение, волна описывается уравнением x  Acos( t) . До точки М, в которой наблюдается интерференция, первая волна в среде с показателем преломления n 1 проходит расстояние S1 и она
 S 
 n S 
будет описываться уравнением x1  A cos   t  1   A cos   t  1 1  . Вторая
v1 
c 


волна в среде с показателем преломления n 2 проходит расстояние S2 и описы S 
 nS 
вается уравнением x 2  A cos   t  2   A cos   t  2 2  . Здесь мы учли, что
v2 
c 


c
c

v1 
и v2 
Следовательно, разность фаз  2  1    n 2S2  n1S1  . Обоc
n1
n2
значим n  S  L и будем называть эту величину оптическим ходом волны. Учи 2
тывая, что
, где  - длина световой волны в вакууме, получим

c 
2
 2  1     , где    L2  L1  оптическая разность хода волн.

16
Если  2  1   2m   , то cos  2  1   1 и в этой точке будет наблюдаться максимум интерференции. Подставляя это условие в найденное значение
разности фаз складываемых колебаний, получим условие наблюдения интерференционного максимума

2  
2.3
 2  m    m    2m  .

2
Максимум интерференции наблюдается в том случае, если оптическая
разность хода волн равна четному числу полуволн или целому числу длин волн.
Если же  2  1     2m   , то

2  
2.4
  2m   
    2m  1 

2
- условие наблюдения интерференционного минимума.
2.2.4. Методы наблюдения интерференции света
1. Метод Юнга. Источником света служит ярко освещенное отверстие
(щель) S, от которой свет падает на две узкие равноудаленные щели S1 и S2 .
Таким образом, световая волна разделяется на две. Интерференция света наблюдается на экране, там, где
световые волны накладываются друг на друга. На
S1
экране наблюдаются темные и светлые полосы. УбеS
диться в том, что мы имеем дело с интерференцией света можно очень
S2
просто.
Если
S
1
одно из отверстий закрыть, то
Рис. 15. Метод Юнга
интерференциS1
онная картина
исчезает.
2. Зеркала и бипризма Френеля.
Свет от источника падает расходящим- S
2
Э
2
ся пучком на два плоских зеркала 1 и 2
расположенных под углом мало отлиРис.16 Бизеркала Френеля
чающимся от 180 . Световые лучи, отраженные от зеркал, можно считать выходящими из мнимых точечных источников
S1
S1 и S2 , являющихся мнимыми изображениями источника S в зеркалах. Поэтому эти
S
источники когерентны и испускаемые ими
волны при наложении будут давать интерференционную картину.
S2
Бипризма Френеля состоит из двух
Рис. 17 Бипризма Френеля
одинаковых,
сложенных
основаниями
призм с малым преломляющим углом. За
17
счет преломления света за бипризмой распространяются лучи, как бы исходящие из двух мнимых источников S1 и S2 , являющихся когерентными. Поэтому
на экране мы будем наблюдать интерференционную картину.
3. Зеркало Ллойда. В опыте, предложенном Ллойдом, интерферируют лучи, исходящие
S
непосредственно от источника света S и отраженные от зеркала. Лучи, отраженные от зеркала, как бы исходят из мнимого точечного источS1
ника света S1 , когерентного S . Для наблюдения
интерференции необходимо, чтобы лучи падали
Рис.18 Зеркало Ллойда
на зеркало под очень большим углом (близким к
90 ).
Особенность интерференционной картины, наблюдаемой в этом случае,
заключается в том, что центральная полоса получается не светлой, а темной.
Это указывает на то, что при отражении света от оптически более плотной среды происходит потеря полуволны (другими словами фаза колебания меняется
на  ).
Следует отметить, что были разработаны и другие способы наблюдения
интерференции света (билинза Бийе, схема В.П. Линника и другие).
3.2.4. Расчет интерференционной картины от двух источников.
Расчет интерференционной картины для всех рассмотренных выше способов можно провести следующим образом. Пусть два когерентных источника
света S1 и S2 расположены на расстоянии d друг от друга, а интерференционная картина наблюдается на экране, удаленном на расстояние L от источников,
причем выполняется условие d  L . Очевидно, что в точке О будет максимум,
так как в эту точку волны приходят в одинаковой фазе (разность фаз равна нулю) и поэтому начало координат поместим в эту точку.
Интенсивность колебания в
x точке М, имеющей координату х,
зависит от разности хода волн
S1
  S2  S1 .
Из
рисунка
L1
2
L2
d

2
2
S1  L   x  
и
2

d
O
2
d

2
2
S2  L   x   . Вычитая из вто2

S2
рого равенства первое, найдем, что
L
S22  S12  2dx .
Учитывая,
что
Рис.19. К расчету интерференции от двух исS22  S12   S2  S1  S2  S1  ,
но
точников.
S2  S1   , а S2  S1  2L окончательно получим
18
dx
.
2.5
L
Подставляя найденное значение разности хода волн, в условие интерференционного максимума 2.3 получим, что максимумы колебаний будут наблюдаться в точках, координаты которых определяются выражением
d  xm
mL
.
2.6
 m    xm 
L
d
Расстояние между соседними максимума (или минимумами) называется
шириной интерференционной полосы x .
L
.
2.7
x  x m1  x m 
d
При этом как видно из 2.7 ширина интерференционной полосы x не зависит от m , и остается величиной постоянной при заданных значениях L, d,  .
Согласно полученному выражению x обратно пропорционально d . Поэтому
для видимого света   107 м  четкая интерференционная картина наблюдает
ся только при выполнении условия d  L .
Из полученных выражений следует, что интерференционная картина
представляет собой чередование светлых и темных полос, параллельных друг
другу. Главный максимум  m  0  расположен в точке О, а симметрично ему
располагаются максимумы первого  m  1 , второго  m  2  и т.д. порядков.
Данная картина наблюдается в случае монохроматического света. Если
же щель осветить белым светом, то максимумы различных цветов будут смещены относительно друг друга  x m   и на экране мы будем наблюдать радужные полосы.
4.2.4. Интерференция света в тонких пленках.
Весьма распространенным случаем интерференции является интерференция световых лучей, отраженных от двух поверхностей прозрачной пластины
(масляные пятна на воде, мыльные пузыри, оксидные пленки и т.д.).
1
2
C
Пусть на плоскопараллельную

пластинку в точке О падает луч света
(рис. 20). В этой точке он разделится на
O
B
два - отраженный и преломленный.
Преломленный луч после отражения в
d
точке А и преломления в точка В снова
i
выходит в воздух. Лучи 1 и 2 отраженные от верхней и нижней поверхности
A
пластинки, когерентны между собой.
Если на их пути поставить собираюРис. 20 Интерференция света в тонкой
пленке
щую линзу, то они сойдутся в некоторой точке фокальной плоскости линзы
19
и дадут интерференционную картину, которая определяется оптической разностью хода между этими лучами.
Оптическая разность хода лучей (как видно из рисунка 20)

2.8
  n  OA  AB  OC  ,
2

где n - показатель преломления пленки, а слагаемое  обусловлено потерей
2
полуволны при отражении света от оптически более плотной среды. Если показатель преломления среды n 0  n , то потеря полуволны происходит в точке О и
берется знак    , в противном случае потеря полуволны происходит в точке А
и берется знак    .
sin 
Учитывая закон преломления света
 n легко показать, что
sin i

2.9
  2d n 2  sin 2   ,
2
где d - толщина пленки,  - угол падения луча.
Из полученного выражения следует,
что при заданных  и n , интерференционная картина зависит от d и  .
1. Полосы равного наклона. При
постоянной толщине пленки разность хода
волн зависит от угла падения лучей на
пленку. Интерференционная картина, возникающая в результате интерференции луРис.21 Полосы равного наклона
чей, падающих на пленку под различными
углами, получила название полос равного
наклона. Полосы равного наклона локализованы в бесконечности и поэтому для
их наблюдения используют собирающую линзу, а экран располагают в ее фокальной плоскости. Если оптическая ось линзы перпендикулярна плоскости
пластины, то линии равного наклона будут иметь вид концентрических окружностей с центром в фокусе линзы.
2. Полосы равной толщины. Рассмотрим отражение света от прозрачной пластины, поверхности которой не параллельны между собой (тонкий
клин). В этом случае также появятся два луча, отраженные от верхней и нижней
поверхности клина, но эти лучи не будут параллельными, а пересекаются в
точке В, вблизи поверхности клина. Поэтому говорят, что полосы равной толщины локализованы на поверхности клина. При малых значениях угла клина
оптическую разность хода волн можно найти по той же формуле 2.9. Если на
пути лучей поставить собирающую линзу, то они будут интерферировать.
Лучи, падающие в другую точку клина под тем же самым углом, будут
собираться линзой в другой точке. Оптическая разность хода волн будет определяться уже другой толщиной пленки. Таким образом, на экране возникает си20
стема интерференционных полос. Каждая из полос возникает за счет отражения
света от мест пластинки, имеющих одинаковую толщину и поэтому называется
полосой равной толщины.
Кольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона, наблюдающиеся при отражении света от тонкого воздушного клина, образованного
плоско параллельной стеклянной плаR
стиной и соприкасающейся с ней
плоско выпуклой линзой с большим
радиусом кривизны. При нормальном
падении света луч отражается от
rm
d верхней и нижней поверхности клина
и при наложении этих лучей образуется интерференционная картина,
Рис. 22 Кольца Ньютона
имеющая вид концентрических колец.
В отраженном свете оптическая разность хода волн будет определяться
толщиной воздушного клина в месте отражения луча d и потерей полуволны
при отражении от нижней границы клина (показатель преломления стекла
больше показателя преломления воздуха), т.е.

2.10
  2d  .
2
2
Из рисунка следует, что R 2   R  d   rm2 . Пренебрегая величиной вто2r
рого порядка малости d 2 можно получить, что d  m и тогда
R
r

2.11
 m  .
R 2
Подставляя в условие интерференционного минимума 2.4, найдем радиус
темных колец Ньютона
rm 

2.12
   2m  1   rm  m  R   .
R 2
2
Из полученного выражения 2.12 следует, что rm зависит от длины волны
 и поэтому при освещении линзы белым светом наблюдается система радужных колец.
Зная радиус кривизны линзы, и измеряя радиус колец Ньютона на опыте
можно определить длину световой волны.
5.2.4. Применение интерференции. Интерферометры.
1. Просветление оптики. При падении света на любую прозрачную поверхность часть света отражается, что приводит к образованию бликов, а также
ухудшает качество изображения, даваемое оптической системой.
21
Для устранения указанных недостатков осуществляют так называемое
просветление оптики. Для этого на поверхность линзы
наносится тонкая прозрачная пленка с показателем
n0
преломления меньшим, чем у линзы. При отражении
света от верхней и нижней поверхности пленки обраn1
зуются два когерентных луча, интенсивности которых
n2
будут одинаковыми, если показатель преломления
пленки удовлетворяет условию n1  n 2 . Так как
Рис.23. Просветлеn 0  n1  n 2 , то потеря полуволны происходит в обеих
ние оптики
точках отражения и оптическая разность хода волн будет определяться выражением   2d  n1 . Толщину пленки подбирают таким
образом, чтобы отраженные лучи давали интерференционный минимум и тогда

 2m  1   .
2dn1   2m  1 
 d
2
4  n1
На практике обычно принимают m  0 , и тогда для минимальной толщины пленки получается значение

.
2.13
dm 
4n1
Так как белый свет имеет сложный
состав и погасить все длины волн невозможно, то делается это для наиболее
восприимчивой глазом части спектра.
Поэтому просветленная оптика в отраженном свете кажется голубой.
Интерферометры. Широкое при1
2 менение явление интерференции нашло
в очень точных измерительных приборах
получивших название интерферометров.
Все они основаны на одном и том же
принципе и различаются лишь конструкS
тивно. Рассмотрим один из них – интерРис. 24. Интерферометр Майкельсона
ферометр Майкельсона.
Свет от источника света S падает
на полупрозрачную пластинку и разделяется на два луча – отраженный 1 и преломленный 2. После отражения от зеркал лучи накладываются и дают интерференционную картину. Для компенсации дополнительной разности хода волн на
пути луча 2 ставится вторая такая пластинка.
Лучи 1 и 2 когерентны и поэтому будут давать интерференционную картину, вид которой зависит от разности хода волн. При перемещении одного из


зеркал на очень малое расстояние  порядка  разность хода лучей изменяется
4


на
и произойдет смена освещенности зрительного поля (на месте максимума
2
22
появляется минимум и наоборот). Таким образом, появляется возможность использовать интерферометр для измерения очень малых (вплоть до 109 м ) длин
отрезков.
Применяя интерферометр, Майкельсон в 1892 году произвел сравнение
международного эталона метра с длиной стандартной световой волны. Данный
метод позволил значительно увеличить точность измерения эталона.
Задачи к зачету
15. В опыте Юнга расстояние между щелями равно 0,8 мм. На каком расстоянии от щелей надо поместить экран, чтобы ширина интерференционной полосы была равна 2 мм?
16. На мыльную пленку  n  1,3 , находящуюся в воздухе, нормально падает
пучок белого света. При какой наименьшей толщине пленки отраженный
свет с длиной волны 0,55 мкм будет максимально ослаблен в результате интерференции?
17. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны 500 нм. Отраженный свет максимально
усилен вследствие интерференции. Определить минимальную толщину
пленки, если показатель преломления равен 1,4.
18. Радиус четвертого темного кольца Ньютона в отраженном свете равен 2 мм.
Определить радиус кривизны линзы, если длина волны 500 нм.
19. На тонкий стеклянный клин падает нормально пучок лучей с длиной волны
500 нм. Расстояние между соседними темными полосами в отраженном свете равно 0,5 мм. Определить угол между поверхностями клина, если показатель преломления стекла 1,5.
20. На тонкую мыльную пленку с показателем преломления 1,33 под углом 30
падает свет с длиной волны 0,6 мкм. Определить угол между поверхностями
пленки, если расстояние между интерференционными полосами в отраженном свете равно 4 мм.
21. В опыте с зеркалами Френеля расстояние между мнимыми изображениями
источника света равно 0,5 мм, а расстояние от них до экрана равно 3 м. В
желтом свете ширина интерференционных полос равна 6 мм. Определить
длину волны желтого цвета.
22. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона в
отраженном свете равно 9 мм. Радиус кривизны линзы 15 м. Определить
длину волны света, падающего на установку.
23. На каком расстоянии от центрального максимума находится третья темная
полоса в опыте Юнга, если расстояние между щелями равно 1,5 мм, расстояние до экрана равно 3 м? Щели освещаются красным светом с длиной волны 0,7 мкм.
24. На поверхность линзы с показателем преломления 1,5 нанесена тонкая
пленка с показателем преломления 1,2. При какой наименьшей толщине
пленки произойдет максимальное усиление отраженных лучей с длиной
волны
0,4 мкм?
23
25. В опыте Юнга расстояние между щелями равно 1 мм, а расстояние от щелей
до экрана равно 3 м. Определить положение первой светлой полосы, если
щели осветить светом с длиной волны 0,5 мкм.
26. На стеклянный клин с показателем преломления 1,5 нормально падает монохроматический свет. Угол клина 4 . Определить длину световой волны,
если расстояние между двумя соседними интерференционными максимума в
отраженном свете равно 0,2 мм
27. На линзу с показателем преломления 1,58 нормально падает монохроматический свет с длиной волны 0,55 мкм. На линзу наносится тонкая пленка с
показателем преломления 1,26. При какой минимальной толщине пленки отраженные лучи будут иметь наименьшую яркость?
28. Расстояние от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной 1 см укладывается 10 темных интерференционных полос. Длина волны 0,7 мкм.
3.4. Дифракция света
1.3.4. Принцип Гюйгенса.
Дифракцией называется явление огибания волнами препятствий, встречающихся на их пути. В более общем смысле
под дифракцией понимается любое отклонение
от законов геометрической оптики при распространении волн. Следует иметь в виду, что дифракция наблюдается в том случае, если размеры препятствия (или отверстия) сравнимы с
Рис. 25. Принцип Гюйгенса
длиной волны. Например, при распространении
волн на поверхности воды за большим препятствием образуется область
геометрической тени, а малое препятствие волны огибают.
Для объяснения процесса распространения волн Гюйгенс сформулировал
принцип,
согласно которому каждая точка среды, до которой доходит возмущение, становится источником вторичных волн, а геометрическая огибающая этих вторичных волн дает положение волнового фронта в последующий момент времени.
Из рисунка 25 видно, что при падении плоской волны на отверстие волновой фронт после отверстия плоский только в средней части, а по краям происходит его загибание, т.е. волна проникает в область геометрической тени.
Явление дифракции характерно именно для волновых процессов. Поэтому, если свет является волновым процессом, то для него должна наблюдаться
дифракция, т.е. световая волна должна проникать в область геометрической тени. Однако, опыт говорит о том, что за непрозрачным предметом образуется
четкая геометрическая тень. Теория Гюйгенса не смогла ответить на этот вопрос.
24
Принцип Гюйгенса является чисто геометрическим, т.е. позволяет определить направление распространения световой энергии. В то же время он ничего не говорит об интенсивности волн, распространяющихся в различных
направлениях. Френель дополнил принцип Гюйгенса физическим содержанием,
добавив в него идею об интерференции вторичных волн, создаваемых фиктивными источниками. Согласно принципу Гюйгенса – Френеля, световая волна,
возбуждаемая каким-либо источником, может быть представлена как результат
суперпозиции вторичных волн, излучаемых фиктивными источниками.
2.3.4. Метод зон Френеля. Закон прямолинейного распространения света.
Первой задачей, которую должен был решить Френель, являлась задача о
прямолинейном распространении света. Френель решил эту задачу, рассмотрев
взаимную интерференцию вторичных волн и применив прием, получивший
название метода зон Френеля.
Найдем амплитуду световой волны, распространяющейся от точечного
источника света S в произвольной точке М. Согласно принци
bm
пу Гюйгенса – Френеля заменим
2
действие источника действием
воображаемых источников, расS
M
положенных на вспомогательa
b
ной поверхности, являющейся
волновым фронтом (в данном
случае, сферой). Разобьем волРис. 26. Образование зон Френеля
новую поверхность на кольцевые зоны так, чтобы расстояния

от краев зон до точки М отличилась бы на
(рис. 26). Так как колебания от со2

седних зон проходят до точки М расстояния, отличающиеся на , то в эту точ2
ку они приходят в противофазах и при наложении будут взаимно ослаблять
друг друга. Поэтому амплитуда результирующего колебания будет определяться следующим образом
A  A1  A 2  A3  ...........  A m .
3.1
Можно показать, что подобное разбиение выделяет зоны одинаковой
площади. Согласно предположению Френеля действие отдельной зоны в точке
М будет тем меньше, чем больше угол  . Кроме того, интенсивность излучения
в направлении точки М уменьшается с увеличением расстояния от зоны до этой
точки. Учитывая оба этих фактора можно получить, что
A1  A 2  A3  ...........  A m .
Общее число зон огромно и поэтому в качестве допустимого приближения можно считать, что амплитуда колебания A m от некоторой m  ой зоны
Френеля равна среднему арифметическому от амплитуд примыкающих зон, т.е.
25
A m1  A m1
.
3.2
2
Учитывая 3.2 мы можем выражение 3.1 преобразовать к виду
A A
A  A
A 
A
3.3
A  1   1  A 2  3    3  A 4  5   .......  m .
2  2
2   2
2 
2
Выражения, стоящие в скобках, равны нулю и пренебрегая слагаемым
Am 
Am
(ввиду его малости) можно получить
2
A
3.4
A 1
2
Таким образом, амплитуда волны со
bm
здаваемой в произвольной точке М сфериrm
a
2
ческой волновой поверхностью равна половине амплитуды, создаваемой одной ценhm
тральной зоной Френеля.
Определим радиус зоны Френеля. Из
рисунка 27 видно, что
2
Рис. 27. К расчету радиуса зоны
2

2

2
Френеля
a   a  h m    b  m    b  h m  . Рас2

крывая скобки и пренебрегая членами второго порядка малости можно полуmb
2
чить h m 
. И тогда r  a 2   a  h m  . Подставляя найденное значение
2a  b
h m , получим окончательно
mba 
.
3.5
2(a  b)
При a  b  0,1 м, получим, что радиус первой зоны будет равен 0,16 мм.
Следовательно, распространение света от источника S к точке М происходит
так, будто световой поток распространяется внутри
очень узкого канала, т.е. прямолинейно.
Правомерность деления волнового фронта на
зоны Френеля была подтверждена экспериментально, с помощью зонной пластинки (рис. 28).
Зонная пластинка представляет собой систему чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу распоРис. 28. Зонная пластинка.
ложения зон Френеля, т.е. с радиусами, определяемыми по формуле 3.5 для данных a, b,  . Если поместить данную пластинку на
расстоянии а от источника света, то в точке, удаленной от пластинки на расстояние равное b зонная пластинка будет создавать интенсивность волны больше,
чем в отсутствии пластинки. Это объясняется тем, что колебания всех зон приходят в точку М в одной фазе и при наложении взаимно усиливают друг друга.
3.3.4. Дифракция Френеля на круглом отверстии и диске.
r
26
Пусть сферическая волна, распространяющаяся от точечного источника
света, встречает на своем пути препятствие с круглым отверстием. Дифракционную картину будем наблюдать на экране, параллельном плоскости отверстия.
Вид дифракционной картины зависит от числа зон Френеля укладывающихся в
отверстии. Если это число четное, то в центре картины будет минимум (темное
пятно), а при нечетном числе зон – максимум (светлое пятно). Это объясняется
тем, что колебания исходящие из соседних зон взаимно ослабляют друг друга,
так как они приходят в эту точку в противофазах.
Если на пути сферической волны поместить непрозрачный диск, то он
будет закрывать первые m зон и поэтому, амплитуда колебаний в центре дифракционной картины будет равна половине амплитуды первой открытой зоны
Френеля, т.е.
A
A  m1 ,
2
т.е. в центре картины всегда будет наблюдаться максимум колебания
(светлое пятно).
Это интересно. В 1818 году при обсуждении мемуара Френеля Пуассон резко заметил, что в центре дифракционной картины от непрозрачного экрана должно быть светлое
пятно, что абсурдно. Однако опыты, специально поставленные Араго, подтвердили выводы
Френеля. Светлое пятнышко в центре геометрической тени, отбрасываемой шариками малого радиуса, наблюдали Маральди (1723 г.) и еще раньше Делиль (1715 г.), но тогда на эти
опытные факты не обратили внимание.
4.3.4. Дифракция Фраунгофера (дифракция в параллельных лучах).
Большое практическое значение имеет дифракция в параллельных лучах.
Она наблюдается в том случае, если источник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию. Чтобы реально осуществить данный вид дифракции достаточно источник света поместить в фокусе собирающей линзы, а дифракционную картину наблюдать в фокальной
плоскости второй собирающей линзы, установленной за препятствием.
В качестве примера рассмотрим дифракцию Фраунгофера на бесконечной
щели (для этого достаточно, чтобы длина
щели была во много раз больше ее ширины).
  a  sin 
Пусть плоская монохроматическая

волна падает нормально на щель шириной
« a ». Оптическая разность хода лучей идущих от краев
щели в произвольном
направлении будет очевидно равна
3.6
  a  sin  .
Разобьем щель на зоны Френеля,
B
имеющие вид полос, параллельных ребру
Рис. 29. Дифракция света на одной щещели. Ширина зоны выбирается так, чтобы
ли.
разность хода лучей от краев соседних зон
27
была равна
N
2
, т.е.


. Тогда на ширине щели будет укладываться число зон равное
2
2a  sin 
.
3.7

Амплитуды колебаний вторичных волн в плоскости щели будут одинаковы, так как выбранные зоны Френеля имеют одинаковую площадь и одинаково
наклонены к направлению наблюдения.
Из полученного выражения 3.7 следует, что число зон Френеля, укладывающихся на ширине щели, зависит от угла  , а от числа зон, в свою очередь,
зависит результат интерференции вторичных волн. Очевидно, что при четном
числе зон Френеля амплитуда результирующего колебания будет равна нулю,
так как колебания от соседних зон будут гасить друг друга, и в данном направлении будет наблюдаться дифракционный минимум. Таким образом, условие
дифракционного минимума будет иметь вид
3.8
a  sin   m .
При нечетном числе зон

3.9
a  sin    2m  1  .
2
будет наблюдаться дифракционный максимум, соответствующий действию

одной зоны Френеля. Из выражения sin  
следует, что расстояние от цен2a
тра картины до первого минимума будет тем больше, чем меньше а.
Таким образом, с уменьшением ширины щели центральная полоса
расширяется. Наоборот, при увеличении ширины щели минимумы приближаются к центру картины, так что центральный максимум становится резче. Если
a  , то на экране мы получим резкое изображение щели.
Положение дифракционных максимумов и минимумов зависит также от
длины волны  и, рассмотренный вид дифракционная картина будет иметь
только в случае монохроматического
излучения. При освещении щели белым светом будет наблюдаться совокупность соответствующих картин для
  ds in 

разных цветов (сдвинутых относительно друг друга). Центральный максимум будет общим для всех картин, поэтому центральный максимум имеет
вид белой полоски.
N
C
Рис. 30. Дифракция света на двух щелях.
28
5.3.4. Дифракционная решетка
Рассматривая дифракцию от одной щели, мы установили, что положение
максимумов и минимумов зависит от угла  и совершенно не зависит от положения самой щели. Поэтому перемещение щели параллельно самой себе не изменяет дифракционной картины. Следовательно, если от одной щели мы перейдем к двум (или многим), то дифракционные картины создаваемые каждой
щелью будут одинаковыми. Очевидно, что в тех направлениях, в которых ни
одна из щелей не распространяет свет, он не будет распространяться и при двух
щелях, т.е. положение главных минимумов будет определяться выражением 3.8
a  sin   m   .
Следует иметь в виду, что кроме интерференции лучей идущих от одной
щели в данном случае имеет место интерференция лучей, распространяющихся
от различных щелей. Если ширина щели равна «а», а ширина непрозрачного
участка « b », то величину d  a  b называют периодом (постоянной) дифракционной решетки. Тогда разность хода лучей идущих от двух соседних щелей,
будут для данного направления  одинаковы и равны
3.10
  d  sin 
и тогда в направлениях, удовлетворяющих условию
3.11
d  sin   m  
будут наблюдаться главные максимумы, а дополнительные минимумы наблюдаются в направлениях удовлетворяющих условию

3.12
d  sin     2m  1 .
2
Таким образом, полная дифракционная картина для двух щелей определяется
следующими условиями
a  sin   m   - главные минимумы,
d  sin   m   - главные максимумы,

- дополниd  sin     2m  1
2
тельные минимумы.
На рисунке 31 показано распределение интенсивности света в дифракциРис. 31. Дифракционная картина
онной картине получаемой от двух щеот двух щелей
лей. Можно показать, что при N щелях
между двумя главными максимума будет
располагаться ( N  1 ) дополнительных минимума, разделенных вторичными
максимумами, создающими весьма слабый фон. Чем больше щелей, тем больше
энергии проходит через дифракционную решетку, тем больше минимумов образуется между главными максимума, тем более интенсивными и более острыми будут сами максимумы.
29
При освещении решетки белым светом все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого расположен ближе к
центру дифракционной картины, красный – наружу.
Это свойство дифракционной решетки широко используется для исследования спектрального состава света.
6.3.4. Разрешающая способность оптических приборов.
Вследствие явления дифракции на оправе оптической системы изображение любой светящейся точки представляет собой дифракционную картину, в
центре которой находится светлое пятно, окруженное чередующимися темными и светлыми полосами. Если мы наблюдаем две точки, то их дифракционные
картины накладываются друг на друга. Как показал Релей, эти точки будут разрешимы (мы их воспринимаем раздельно), если максимум от одной картины
накладывается на минимум другой. При этом глубина провала составляет
0,8I m , что достаточно для разрешения этих точек.
Можно показать, что точки разрешимы, если угловое расстояние между
ними удовлетворяет условию
S1
S2

3.13
d  1,22 .
D
Разрешающей способностью оптиd
ческой системы называется величина
1
D
,
3.14
R

d 1,22  
т.е. зависит от диаметра оптической системы и длины волны света. Для
увеличения разрешающей способности
надо либо увеличивать диаметр оптической системы, либо уменьшать длину
волны.
Рис. 31. К разрешающей способности
объектива
Задачи к зачету
29. На дифракционную решетку нормально падает белый свет. На какую длину
волны в спектре третьего порядка накладывается красная линия    670 нм 
в спектре второго порядка?
30. Какова постоянная дифракционной решетки, если максимум первого порядка для света с длиной волны 546 нм наблюдается под углом 19 ?
31. Найти наибольший порядок максимума для света с длиной волны 589 нм,
если постоянная дифракционной решетки равна 2 мкм.
32. На узкую щель шириной 0,05 мм падает нормально свет с длиной волны 694
нм. Под каким углом будет наблюдаться второй дифракционный максимум?
30
33. Посередине между источником света и экраном находится диафрагма с
круглым отверстием. Определить радиус отверстия, при котором центр дифракционной картины является наиболее темным, если расстояние между
источником и экраном равно 1 м, а длина волны 500 нм.
34. Точечный источник света с длиной волны 0,5 мкм расположен на расстоянии 1 м от круглого отверстия радиусом 1 мм. На каком расстоянии от отверстия находится экран, если открыты только первые три зоны Френеля?
35. На диафрагму с круглым отверстием радиусом 1,4 мм падает плоская волна
   0,7 мкм  . На каком минимальном расстоянии от отверстия должен
находиться экран, чтобы в центре дифракционной картины наблюдалось
наиболее темное пятно?
36. На диафрагму с круглым отверстием радиусом 1,4 мм падает плоская волна
   0,7 мкм  . На каком минимальном расстоянии от отверстия должен
находиться экран, чтобы в центре дифракционной картины наблюдалось
наиболее светлое пятно?
37. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен
на угол 14 . На какой угол отклонен максимум третьего порядка?
38. При освещении дифракционной решетки белым светом спектры второго и
третьего порядка частично перекрывают друг друга. На какую длину волны
в спектре второго порядка накладывается фиолетовая    0,4 мкм  спектра
третьего порядка?
39. На дифракционную решетку содержащую 500 штрихов на 1 мм, нормально
падает белый свет   ф  0,4 мкм,  к  0,78 мкм  . Определить ширину спектра первого порядка на экране удаленном на 3 м от решетки.
40. Определить число штрихов на 1 мм дифракционной решетки, если углу в
30 соответствует максимум четвертого порядка для света с длиной волны
0,5 мкм.
41. На щель шириной 0,1 мм нормально падает свет с длиной волны 0,6 мкм.
Экран, на котором наблюдается дифракционная картина, расположен на расстоянии 1 м от нее. Определить расстояние между первыми дифракционными максимума, расположенными по обе стороны от центрального максимума.
42. На щель шириной 0,1 мм нормально падает свет с длиной волны 0,6 мкм.
Экран, на котором наблюдается дифракционная картина, расположен на расстоянии 1 м от нее. Определить расстояние между первыми дифракционными максимума, расположенными по обе стороны от центрального максимума.
31
4.4. Поляризация света.
1.4.4. Естественный и поляризованный свет
Свет представляет собой поперечные электромагнитные волны, в которых векторы Е и H
E
колеблются во взаимно перпендикулярных
направлениях и перпендикулярны вектору скоv
рости распространения волны v (рис. 33). Поэтому для полного описания состояния поляризации светового пучка достаточно знать поведеH
ние одного из этих векторов. Чаще всего расРис. 33. Электромагнитная
суждения ведутся относительно вектора Е (свеволна
товой вектор). Это связано с тем, что взаимодействие света с веществом обусловлено именно
электрической составляющей электромагнитной волны. Плоскость, в которой
колеблется световой вектор, называется плоскостью поляризации.
Световая волна, излучаемая источником, представляет собой излучение огромного числа атомов, каждый из которых излучает свет независимо от других атомов. Поэтому в
световой волне присутствуют колеа)
б)
в)
бания всевозможных направлений.
Рис. 34. а) Естественный, б) частично поляри- Свет со всевозможными и равноверозованный, в) плоско поляризованный свет
ятными направлениями колебаний
светового вектора получил название естественного света.
Свет, в котором колебания светового вектора, каким либо образом упорядочены (в результате внешнего воздействия) называется поляризованным.
Если колебания светового вектора происходят в одной плоскости, то такой свет называется плоско поляризованным.
За меру поляризации света принимается величина называемая степенью
поляризации
I I
4.1
P  max min ,
Imax  Imin
где I max , I min - интенсивность колебания в двух взаимно перпендикулярных направлениях. В частности для естественного света Р = 0, так как
I max  I min , а для плоско поляризованного света Р = 1, так как I min  0 .
Естественный свет можно преобразовать в плоско поляризованный, используя для этого так называемые поляризаторы, пропускающие колебания
только одного направления, например, кристаллы турмалина.
Рассмотрим следующий опыт. Если на пути светового луча поставить
пластинку, определенным образом вырезанную из кристалла турмалина, то при
вращении пластинки вокруг направления распространения луча, мы не заметим
32
ни каких изменений в интенсивности луча, прошедшего через пластинку. Таким образом, световая волна, падающая на турмаI
лин от обычного источника, не обнаруживает
II
асимметрии по отношению к направлению распространения. Иначе будет обстоять дело, если на
пути луча, вышедшего из первой пластинки установить вторую такую же пластинку (рис. 35). В заРис. 35. К закону Малюса.
висимости от того, как ориентированы эти пластинки интенсивность света, вышедшего из второй пластинки, меняется от максимальной (пластинки параллельны) до нуля (полное гашение) (пластинки взаимно перпендикулярны). Малюс на опыте установил, что интенсивность света,
прошедшего вторую пластинку изменяется по закону
4.2
I  I0  cos 2  ,
где I0 - интенсивность света, падающего на вторую пластинку.
Результаты этого опыта можно объяснить следующим образом. Первая
пластинка, пропуская свет только одного направления, преобразует естественный свет в плоско поляризованный и поэтому называется поляризатором.
Вторая пластинка служит для определения степени поляризации света и называется анализатором. Если оптические оси поляризатора и анализатора параллельны, то свет проходит через анализатор без изменения. Если оптическая ось
анализатора перпендикулярна оптической оси поляризатора, то анализатор не
пропускает колебаний и интенсивность света, проходящего через вторую пластинку, будет равна нулю.
Если естественный свет с интенсивностью I ест пропустить через две пластинки, то интенсивность света, вышедшего из первой пластинки и падающего
1
на вторую пластинку будет I0   Iест , и тогда закон Малюса будет иметь вид
2
1
4.3
I   Iест  cos 2  .
2
2.4.4. Поляризация света при отражении и преломлении света.
При падении света на границу раздела двух диэлектриков наблюдается
явление отражения и преломления света. Если на пути отраженного и преломленного лучей поместить анализатор, то можно убедиться в том, что эти лучи
частично поляризованы. При этом в отраженном луче преобладают колебания
перпендикулярные плоскости падения луча, в преломленном луче – колебания
параллельные плоскости падения луча. Степень поляризации лучей зависит от
угла падения луча. Как показал Брюстер, при угле падения удовлетворяющем
условию
tg  n 21
отраженный луч полностью поляризован, а преломленный луч, максимально
поляризован. При этом отраженный и преломленный лучи взаимно перпендикулярны.
33
3.4.4. Двойное лучепреломление
а)
б)
Рис. 36. Ход лучей в кристалле исландского шпата.
Явление двойного лучепреломления было обнаружено Бартолином на кристаллах исландского шпата. Кристаллы турмалина встречаются в естественном состоянии в виде довольно больших и оптически чистых образцов
и, поэтому до настоящего времени исландский
шпат является наилучшим материалом для изготовления оптических приборов, использую-
щих поляризацию света.
Если на толстый кристалл исландского шпата направить луч света, то из
кристалла выйдут два пространственно разделенных луча, даже в том случае,
если угол падения равен нулю (рис. 36). Один из этих лучей является продолжением падающего и поэтому получил название обыкновенного, а второй отклоняется, и поэтому получил название необыкновенного. При вращении кристалла вокруг направления падающего луча, то один из преломленных лучей
(обыкновенный) будет неподвижным, а второй (необыкновенный) будет вращаться вокруг первого. Различие в отклонении обоих лучей показывает, что
они обладают различными показателями преломления. При исследовании явления двойного лучепреломления было установлено, что обыкновенный луч имеет один и тот же показатель преломления для всех направлений, а показатель
преломления необыкновенного луча зависит от направления в кристалле.
Если исследовать оба луча с помощью анализатора, то можно обнаружить, что оба луча поляризованы, и притом во взаимно перпендикулярных
направлениях.
4.4.4. Поляризационные призмы и поляроиды.
Поляризованный свет получил широкое практическое применение. Задача получения плоско поляризованного света состоит в пространственном разделении обыкновенного и необыкновенного лучей. Практически эта задача решается двумя способами:
- поляризационные призмы;
- поляроиды.
Призма Николя (рис. 37) представляет собой
Рис. 37. Призма Николя кристалл исландского шпата, разрезанный по малой
диагонали и склеенный канадским бальзамом. Показатель преломления канадского бальзама (1,550) лежит между значениями показателя преломления обыкновенного (1,658) и необыкновенного (1,486) лучей.
При соответствующем подборе угла падения обыкновенный луч испытывает
полное отражение на слое канадского бальзама и поглощается зачерненной поверхностью призмы. Необыкновенный луч не испытывает полного отражения и
выходит из призмы.
34
Многие кристаллы обладают свойством дихроизма, т.е. различного поглощения обыкновенного и необыкновенного лучей. На явлении дихроизма
были изобретены поляроиды. Если на тонкую прозрачную пленку нанести кристаллы герапатита, то уже при толщине слоя кристаллов 0,1 мм обыкновенный
луч полностью поглощается, а интенсивность необыкновенного луча не изменяется.
5.4.4. Искусственная оптическая анизотропия
Двойное лучепреломление наблюдается в естественных анизотропных
средах. Существуют, однако, и различные способы получения искусственной
оптической анизотропии.
Как показывает опыт, оптически изотропные среды становятся оптически
анизотропными под действием различных факторов, например,
- механическое напряжение - n 0  n n  k ;
- электрического поля (эффект Керра) - n 0  n n  kE 2 ;
- магнитного поля - n 0  n n  kH2 .
Наибольший интерес представП
А

ляет случай возникновения оптической анизотропии под действием
электрического поля или эффект Кер
ра. Ячейка Керра (кювета заполненРис. 38. К эффекту Керра
ная жидкостью и два электрода) помещается между двумя скрещенными николями и поэтому свет через систему
не проходит (рис. 38). Если же на электроды подать напряжение, то жидкость
становится анизотропной и, свет будет проходить через систему. При изменении напряжения на электродах будет изменяться и интенсивность света, проходящего через систему. Эффект Керра – оптическая анизотропия вещества под
действием электрического поля объясняется различной поляризуемостью молекул жидкости по различным направлениям. Это явление практически безинерционно, т.е. переход из одного состояния в другое происходит за время порядка
1010 с (практически мгновенно). Поэтому ячейка Керра служит идеальным световым затвором и широко применяется в исследовании быстропеременных
процессов (фото и киносъемка, запись и воспроизведение звука, оптиковолоконная связь и др.).
6.4.4. Вращение плоскости поляризации.

Рис. 39. Вращение плоскости поляризации.
35
Некоторые вещества в твердом и жидком состоянии обладают способностью вращать плоскость поляризации света. Такие
вещества получили название оптически активных веществ.
Мы уже указывали на то, что свет не проходит через скрещенные николи
и поле зрения будет темным. Если же между анализатором и поляризатором
поместить кювету с оптически активным веществом, то поле зрения просветляется. Чтобы снова его сделать темным, анализатор надо повернуть на некоторый угол  (рис.39). Угол  и есть тот угол, на который поворачивает плоскость поляризации оптически активное вещество.
Опыт показывает, что для твердых тел угол поворота плоскости поляризации определяется по формуле
4.4
   ,
где
- расстояние, проходимое светом в среде,  - удельное вращение, т.е.
угол на который поворачивается плоскость поляризации на пути в 1 метр. Для
растворов
4.5
  C ,
где С – концентрация оптически активного вещества.
Это явление широко применяется для определения концентрации вещества (например, сахара в крови человека).
Задачи к зачету
43. Пучок света, идущий в воздухе, падает на поверхность жидкости под углом
54 . Определить угол преломления лучей, если отраженный луч полностью
поляризован.
44. Пучок естественного света падает на стекло с показателем преломления
равном 1,73. Определить, при каком угле преломления отраженный от стекла пучок света будет полностью поляризован.
45. Естественный свет проходит через поляризатор и анализатор, поставленные
так, что угол между их главными плоскостями равен  . Как анализатор, так
и поляризатор поглощают и отражают по 8% падающего на них света. Оказалось, что интенсивность света, вышедшего из анализатора равна 9% интенсивности естественного света, падающего на поляризатор. Найти угол  .
46. Угол  между плоскостями пропускания николей равен 45 . Во сколько
раз уменьшится интенсивность света, выходящего из анализатора, если этот
угол увеличить до 60 ?
47. Определить во сколько раз ослабится интенсивность света, прошедшего два
николя, расположенные так, что угол между их главными плоскостями равен
60 , а в каждом николе теряется 8% интенсивности падающего света.
48. Угол между главными плоскостями двух николей равен 60 . Естественный
свет, проходя такую систему, ослабляется в 16 раз. Пренебрегая потерей
света при отражении, определить коэффициент поглощения света в николях.
49. Пластинка кварца толщиной 2мм помещена между двумя скрещенными николями. Пренебрегая потерями света в николях, определить, во сколько раз
уменьшится интенсивность света, прошедшего эту систему? Удельное вращение кварца 15 град мм .
50. Плоско поляризованный свет, прошедший через поляроид, оказывается
полностью погашенным. Если же на пути света поместить кварцевую пла36
стинку, то интенсивность света, прошедшего через поляроид, уменьшается в
3 раза. Определить минимальную толщину кварцевой пластинки.
51. Пластинка кварца толщиной 2 мм поворачивает плоскость поляризации света на угол 53 . Какой толщины пластинку надо взять, чтобы повернуть
плоскость поляризации на угол 180 ?
52. Раствор глюкозы с концентрацией 280 кг м3 содержащийся в стеклянной
трубке, поворачивает плоскость поляризации света на угол 32 . Определить
концентрацию глюкозы в другом растворе, налитом в трубку такой же длины, если он поворачивает плоскость поляризации на угол 24 .
53. При прохождении света через трубку длиной 20 см, содержащую десяти
процентный раствор сахара, плоскость поляризации поворачивается на угол
13,3 . В другом растворе сахара, налитом в трубку длиной 15 см плоскость
поляризации поворачивается на угол 5,2 . Определить концентрацию второго раствора.
54. Определить угол полной поляризации для стекла, показатель преломления
которого равен 1,57.
55. Предельный угол полного отражения для некоторого вещества равен 45 .
Чему равен для этого вещества угол полной поляризации?
56. Доказать, что при падении света на границу раздела двух прозрачных сред
под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.
5.4. Элементы теории относительности.
1.5.4. Скорость света и ее опытное определение.
Задача определения скорости света принадлежит к числу важнейших
проблем оптики и физики вообще.
Решение этой задачи имело принципиальное и практическое значение.
Установление того факта, что скорость распространения света конечна, и измерение этой скорости сделали более конкретными и ясными трудности, стоящие
перед различными оптическими теориями.
Сравнительное измерение скорости света в пустоте и различных средах
послужило в свое время в качестве экспериментального сравнения волновой и
корпускулярной теорий света.
Сравнение скорости света в пустоте с константой «с» (скоростью распространения электромагнитных волн) в электромагнитной теории Максвелла,
сыграло важную роль в обосновании электромагнитной теории света.
Наконец, вопрос о влиянии движения системы на скорость распространения света и вся обширная совокупность связанных с ним экспериментальных и
теоретических проблем привели к пересмотру наших представлений о пространстве и времени – специальной теории относительности – одного из самых
значительных обобщений теоретической физики, имеющего исключительное
значение для развития физики.
37
Основная трудность, с которой сталкивается экспериментатор при определении скорости света, связана с огромным значением этой величины. Поэтому первое определение скорости света предпринятое Г.Галилеем не принесло
успеха.
Идея Галилея заключалась в следующем. Пусть на некотором расстоянии
L находятся два наблюдателя с фонарями с открывающимися крышками.
Пусть первый наблюдатель открывает фонарь и включает часы. Второй наблюдатель после прихода света мгновенно открывает крышку своего фонаря и пер2L
вый наблюдатель, увидев свет, останавливает часы. И тогда v 
. Однако,
t
экспериментально осуществить эту идею не удалось.
Первым удачным опытом по определению скорости света, давшим
надежную цифру, близкую к современному значению, было определение датского астронома Ремера в 1676 году. Метод Ремера основан на астрономических наблюдениях за спутником Юпитера ИО. Ремер наблюдал, что промежуток времени между двумя последовательными затмениями спутника оказываются несколько большими, когда Земля удаляется от Юпитера и несколько
меньшими, когда Земля приближается к Юпитеру. Ремер объяснил это тем, что
свету требуется дополнительное время на прохождение расстояния между
Юпитером и Землей. При удалении Земли это время надо прибавлять к истинному периоду обращения, а при приближении вычитать. В ходе своих наблюдений Ремер получил значение скорости света равное 225000 км с .
В 1849 году Физо реализовал идею Г.Галилея в которой автоматически
регистрировался момент пуска и возвращения сигнала, осуществляемый путем
регулярного прерывания светового потока (метод прерываний).
Свет от источника света проходит между зубьями колеса отражается от
зеркала расположенного на расстоянии L от колеса и попадает в глаз наблюдателя. Если колесо вращается, и при том с такой угловой скоростью, что на место просвета станет зуб, то наблюдатель света видеть не будет (первое затмение). Если ширина зуба и просвета одинаковы, то при удвоенной скорости вращения наблюдатель будет наблюдать максимум интенсивности света. При
утроенной скорости вращения будет наблюдаться второе затмение, так как на
место прорези станет следующий зуб и так далее.
Главная трудность состоит в точном определении момента затмения.
Точность значительно повышается при увеличении базы и наблюдении затмений высокого порядка. В 1902 году Перротен на базе в 46 км наблюдал затмения 32 порядка и получил для скорости света значение 299780  50 км с .
В начале 19 века Араго предложил метод вращающегося зеркала, который был реализован Физо в 1849 году.
Майкельсон усовершенствовал метод вращающегося зеркала. Применение метода вращающегося зеркала позволило значительно сократить базу, что
дало возможность определения скорости света в среде.
38
2.5.4. Принцип относительности Галилея и законы электродинамики
Физические законы, в том числе, и законы механики, имеют определенный смысл лишь тогда, когда точно определимы реальные условия протекания
рассматриваемых явлений и, следовательно, указана система отсчета, к которой
они отнесены.
Мы уже указывали, что законы движения формулируются одинаково
только в инерциальных системах отсчета. Это видно из того факта, что в основdv
ной закон динамики (второй закон Ньютона) F  m 
входит ускорение тела,
dt
а не его скорость. Таким образом, добавление любой постоянной скорости, т.е.
переход от одной системы отсчета к другой, не отражается на формулировке
второго закона Ньютона. Необходимость определить систему отсчета, для которой сформулированы законы механики, заставила Ньютона ввести понятие
абсолютного пространства как такой исходной системы. Однако все системы
отсчета, движущиеся равномерно и прямолинейно относительно этого пространства, допускают такую же формулировку законов механики и являются с
точки зрения механики эквивалентными друг другу.
Таким образом, наблюдения над механическими процессами не позволяют обнаружить движение одной инерциальной системы относительно другой –
принцип относительности в механике (принцип относительности Галилея).
При переходе от одной инерциальной системы отсчета к другой ускорение тела остается постоянным, но координаты и скорость тела изменяются. Для
установления связи между ними служат формулы преобразования. В классической механике это преобразования Галилея.
Пусть система K  движется относительно системы K с постоянной скоростью v0 , направленной вдоль оси X . Тогда преобразования Галилея будут
иметь вид
x  x  v 0  t
x  x  v 0  t
y  y
y  y
z  z
z  z
t  t
t  t
Инвариантность уравнений механики по отношению к этим преобразованиям и есть математическое выражение принципа относительности
Подобным образом строится и электродинамика. Опираясь на опыт, формулируются основные законы электродинамики (уравнения Максвелла), выбирается система отсчета, и указываются формулы преобразований, позволяющие
переходить от одной системы отсчета к другой.
Что касается формул преобразования, то преобразования Галилея считались вполне очевидными и были перенесены в новую теорию. Система отсчета
– особая среда – мировой эфир, так как для распространения волн требуется
определенная среда. Основной вопрос: Как движение тел влияет на мировой
эфир? И еще один вопрос – уравнения Максвелла не инвариантны относительно преобразований Галилея, а это означает, что механический принцип относи39
тельности нельзя распространить на электромагнитные (в частности, оптические) явления.
Из создавшейся ситуации можно было выйти несколькими путями. Рассмотрим наиболее известные.
1. Герц переносит механический принцип относительности в электродинамику и, используя преобразования Галилея, изменяет уравнения электродинамики так, чтобы они были инвариантными относительно этих преобразований. Это означает, что эфир полностью увлекается движущимися телами. Однако выводы Герца противоречили целому ряду опытных фактов.
2. Лоренц считал, что уравнения Максвелла справедливы, а принцип относительности неверен. Эфир неподвижен. Иными словами это означает признание существования абсолютной системы отсчета – мирового эфира и признание того факта, что можно обнаружить движение одной системы отсчета относительно эфира (подобно тому, как мы определяем движение автомобиля по
движению воздуха за окном). Экспериментальная проверка была осуществлена
Майкельсоном.
Рассмотрим механический пример. Пусть моторная лодка проходит расстояние между двумя точками туда и обратно, двигаясь по течению реки и обS
S
2Sv
ратно, затрачивая на это время t1 
. Если же лодка будет

 2
v  u v  u v  u2
двигаться в направлении перпендикулярном течению, то на прохождение этого
2S
же расстояния туда и обратно она затратит время t 2 
. Легко показать,
v2  u 2
t
1
 1 . Другими словами, время, затрачиваемое лодкой на движечто 1 
t2
u2
1 2
v
ние во взаимно перпендикулярных направлениях, будет различным.
Используя эту идею и изобретенный им прибор (интерферометр) Майкельсон попытался обнаружить эфирный ветер, связанный с тем, что Земля
движется относительно Солнца, со
скоростью порядка 30км с . Интерферометр можно расположить так, что бы
луч 1 распространялся вдоль скорости
движения Земли. Тогда луч 2 будет
распространяться в направлении перпендикулярном движению Земли (рис.
1
2 40). На прохождение одинакового расстояния они затратят разное время и
между ними установится определенная
разность фаз, что приведет к возникновению интерференционной картины.
S
Если теперь прибор медленно поверРис. 40. Интерферометр Майкельсона
нуть на 90 , то лучи меняются местами
и интерференционная картина должна
40
измениться (сместиться). Однако опыт показал, что никакого смещения интерференционных полос не происходит. В последних опытах Майкельсона чувствительность метода была доведена до такого предела, что можно было обнаружить движение Земли со скоростью 1 км с . Из опыта Майкельсона следовало, что скорость распространения света не зависит от скорости движения источника или приемника света.
Отрицательный результат опыта Майкельсона имел для развития физики
принципиальное значение и требовал объяснения.
2.5.4. Преобразования Лоренца.
Многочисленные попытки объяснить отрицательный результат опыта
Майкельсона в рамках классической физики не принесли успеха.
Кардинальный выход из создавшегося положения был предложен
А.Эйнштейном в 1905 году.
Эйнштейн предложил постулировать два положения. В первом из них механический принцип относительности распространяется на явления природы –
никакими опытами нельзя обнаружить движение одной инерциальной системы относительно другой – принцип относительности Эйнштейна.
Во втором постулируется (коль не можем доказать) опытный факт
постоянства скорости света – скорость света в вакууме не зависит от скорости движения источника и приемника света и является предельной скоростью передачи информации.
Эти постулаты находятся в кажущемся противоречии друг с другом. Рассмотрим следующий мысленный эксперимент. Пусть система К движется относительно системы К со скоростью u направленной вдоль оси x . В момент
времени t  0 эти системы совпадают и в этот момент в начале координат происходит вспышка света и сферическая световая волна начинает распространяться в пространстве. Согласно первому постулату скорость света в обеих системах отсчета одинакова ( c  const ). Согласно второму постулату вид световой
волны должен быть одинаков как в первой системе отсчета, так и во второй.
Другими словами в момент времени t световая волна должна быть представлена сферой с радиусом c  t , имеющей центр как в точке О, так и в точке O , что
явно не может иметь места, так как к этому времени точки О и O разойдутся
на некоторое расстояние равное u  t .
Причина указанного противоречия, по мнению Эйнштейна, лежит не в
противоречии между постулатами, а в допущении, что положение волны относится к одному и тому моменту времени. Это допущение заключено в преобразованиях Галилея, т.е. t1  t 2 . Однако справедливость преобразований Галилея
не доказана.
Рассуждения, в которых играет роль время, покоятся, как показал Эйнштейн, на представлении об одновременности: момент времени устанавливается по показаниям эталонных часов одновременными с этим моментом.
Установление одновременности имеет ясный смысл только в том случае,
когда идет речь об одновременности событий происходящих в одной точке.
41
События одновременны, если они совпадают друг с другом. Однако такой метод совпадений не применим для пространственно разделенных событий.
Снабдив различные точки часами, мы можем по методу совпадений определять время событий только в каждой из этих точек. Но чтобы сопоставить эти
события нужно согласовать ход часов в различных точках, т.е. синхронизировать часы. Можно было согласовать ход всех часов в одной точке и после этого
разнести их по различным точкам. Но мы не знаем, как повлияет перенос на их
ход. Поэтому необходимо разнести все часы, а затем синхронизировать их ход с
помощью некоторого сигнала. В классических преобразованиях считается что
скорость распространения сигнала бесконечна, чего нет на самом деле.
Анализ явлений в инерциальных системах отсчета, проведенный
А.Эйнштейном, показал, что преобразования Галилея несовместимы с ними и,
следовательно, должны быть заменены преобразованиями, удовлетворяющими
этим постулатам.
Рассмотрим две системы отсчета К и К .
y y
Пусть в начальный момент времени эти системы
совпадают и из начала отсчета (точка О) излучается импульс света в направлении оси Х. Согласx
A
но второму постулату Эйнштейна скорость света
x
O O
одинакова в обеих системах отсчета и равна «с».
Рис. 41. К преобразованиям
Поэтому, если в системе К за время t сигнал
Лоренца
дойдет до точки А, пройдя расстояние x  c  t , то
в системе K  координата светового импульса будет x  c  t , т.е. x  x . Отсюда следует, что t  t , т.е. время течет по разному
в различных системах отсчета.
Привычность преобразований Галилея, которыми в физике и механике
пользовались в течение нескольких столетий, привела к тому, что эти преобразования казались вполне естественными и свободными от каких-либо допущений. В действительности, эти преобразования покоятся на допущении о том,
что время течет одинаково во всех инерциальных системах отсчета. Если бы
это было так, то постулаты А.Эйнштейна оказались бы в противоречии друг с
другом.
Заслуга А.Эйнштейна состояла в том, что он показал совместимость этих
постулатов, если отказаться от преобразований Галилея и заменит их другими,
полученными путем математической обработки этих постулатов.
x  vt
x  vt
x 
x
1  2
1  2
y  y
y  y
,
5.1
z  z
z 
vx
v  x
t 2
t  2
c
c
t 
t
2
1 
1  2
42
v
.
c
Эти преобразования получили название преобразований Лоренца.
Нужно иметь в виду, что преобразования Лоренца не отрицают преобразований
v2
Галилея. В предельном случае v  c и   2  0 преобразования Лоренца пеc
реходят в классические преобразования (принцип соответствия).
Из преобразований Лоренца следует, что при v  c координата Х и
время t теряют физический смысл (становятся мнимыми). Это согласуется со
вторым постулатом Эйнштейна о том, что движение со скоростью большей
скорости света в пустоте невозможно.
где  
Интересно отметить тот факт, что формулы полученные Эйнштейном совпадают с
формулами, ранее указанными Лоренцем. Лоренц в своих исследованиях по электродинамике движущихся сред обратил внимание на то, что вычисления упрощаются и в ряде случаев
формулы приобретают инвариантный характер, если при переходе от одной инерциальной
системы отсчета к другой вместо переменной t ввести переменную t  t 
v
x которую он
c2
называет местным временем (в отличие от универсального времени t ). Поэтому эти формулы и называют преобразования Лоренца.
Однако для Лоренца уравнения преобразования были лишь вспомогательными формулами, облегчающими вычисления и не имеющими физического содержания. Сам Лоренц
признавался: Теория Эйнштейна электромагнитных явлений в движущихся средах приобрела
простоту, которой я не мог достигнуть. Главной причиной моей неудачи была моя приверженность к идее, что только переменная t может считаться истинным временем и что мое
местное время t  должно рассматриваться не более чем вспомогательная математическая величина.
3.5.4. Следствия из преобразований Лоренца.
Из преобразований Лоренца вытекает ряд следствий.
1. Относительность одновременности.
Пусть в системе К в точках с координатами x 1 и x 2 происходят два события в моменты времени t1 и t 2 . В системе K  им соответствуют координаты x1
и x2 , моменты времени t1 и t2 .
Если события происходят в одной точке  x1  x 2  и являются одновременными  t1  t 2  , то в соответствии с преобразованиями Лоренца x1  x2 и
t1  t2 , т.е. эти события будут одновременными и системе K  .
Если же эти события в системе К пространственно разделены (x1  x 2 ) ,
но одновременны ( t1  t 2 ), то в системе K  им будут соответствовать моменты
v
v
t1  2 x1
t2  2 x2
c
c
времени t1 
и t2 
, и это означает, что t1  t2 . Другими сло2
2
1 
1 
вами одновременность пространственно разделенных событий относительна.
43
2. Относительность промежутков времени.
Пусть в некоторой точке системы К, происходит событие, длительность
которого   t 2  t1 . Длительность этого же события в системе K  будет равна
v
v
t2  2 x
t1  2 x
c
c
  t2  t1 . Но согласно преобразованиям Лоренца t2 
, t1 
и
2
1 
1  2
тогда
t t

.
5.2
  2 1 
1  2
1  2
Из полученного выражения следует, что длительность события наименьшая в системе отсчета, относительно которой, оно покоится. Другими словами
часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.
3. Относительность длин отрезков.
Пусть стержень, покоящийся относительно системы K  имеет длину


 x 2  x1 . Со0  x 2  x1 . Тогда длина этого стержня в системе K будет равна
x  vt x1  vt
гласно преобразованиям Лоренца 0  x2  x1  2
.


2
2
2
1 
1 
1 
Отсюда
5.3
 0 1  2 ,
т.е. длина стержня, измеренная в системе относительно которой он движется, оказывается меньше длины покоящегося стержня.
4. Релятивистский закон сложения скоростей.
Относительность промежутков времени и длин отрезков ведет к радикальному пересмотру всей кинематики. Прежде всего, это касается классического закона сложения скоростей, так как согласно второму постулату Эйнштейна движение со скоростью большей скорости света в вакууме невозможно.
Если в системе K движение в каждый момент времени t задается координатами  x, y,z  , то в системе K  в моменты времени t  координатами
(x, y, z) , то
dx
dx
ux 
ux 
dt
dt
v .
  2 x
t
x  vt
c
x
t
2
1 
1  2
44
Дифференцируя
два последних равенства можно найти, что
v
  2 dx
dt
dx  vdt
c
dx 
dt 
и тогда после несложных математических пре2
2
1 
1 
образований получим
dx
v
dx  vdt
u  v

dt
ux 

 x
.
5.4
v
v dx
v  ux
dt  2 dx 1  2
1 2
c
c dt
c
Мы получили закон сложения скоростей в релятивисткой механике. Очевидно, что при v  c он переходит в классический закон сложения скоростей.
Из полученного выражения следует, что u x  c даже в том случае, если
cc
ux  v  c , u x 
 c.
11
5. Интервал между событиями.
Все сказанное выше говорит о том, что теория относительности представляет собой стройную систему, которая не только устраняет кажущиеся противоречия между отдельными экспериментальными фактами, но и приводит к
пересмотру наших представлений о пространстве и времени.
В классической механике (механике Ньютона) абсолютное пространство
и абсолютное время никак не связаны между собой. Относительный характер
промежутков времени и длин отрезков означает, лишь относительность отдельных компонент некоторой реальной величины, которая как целое имеет вполне
определенный реальный физический смысл, не зависящий от выбора системы
отсчета, т.е. являющейся инвариантной по отношению к преобразованиям Лоренца. По мнению Эйнштейна в четырехмерном пространстве, в котором каждое событие характеризуется четырьмя координатами  x, y,z, t  , такой величиной является интервал между событиями
s  c2 t 2 
,
5.5
  y 2  y1    z 2  z1  .
Можно показать, что при переходе от одной системы отсчета к другой
интервал между событиями не изменяется.
где

 x 2  x1 
2
2
2
2
4.5.4. Зависимость массы от скорости. Взаимосвязь массы и энергии.
dp
инвариантный относительно преобразоваdt
ний Галилея становится не инвариантным относительно преобразований Лоренца. Эйнштейн показал, что второй закон Ньютона будет инвариантен относительно преобразований Лоренца, если импульс тела будет определяться по
формуле
Второй закон Ньютона F 
45
m0 v
p  mv 
.
5.6
1 
Это говорит о том, что масса тела зависит от скорости движения
m0
.
5.7
m
1  2
Преобразование этого выражения приводит нас к следующему выводу
 2 

m0
v2 
m
 m 0 1    m 0 1  2  .
2
2
1 

 2c 
2
Это выражение можно записать в виде
m0 v2
mc  m 0c 
.
5.8
2
Мы получили выражение фундаментального закона природы - взаимосвязи массы и энергии - E  m  c2 . E0  m0c2 - энергия покоя. И тогда E  E 0  T .
Преобразование выражения 5.7 приводит нас еще к одному выводу:
2
 mc 
2 2
2
m c 

2 2
0
1  2
E 2  E 22  E 02
E 02
 E 
1  2
2
 E 2  E 02  E 22
m2  c4  v2
Так как E  
 m2  v2  c2  p2  c2 . Тогда
2
c
2
E  E02  p2  c2  E 2  p2  c2  E02 .
Мы получили закон сохранения энергии-импульса.
2 2
5.9
6.4. Тепловое излучение.
1.6.4. Тепловое излучение и его характеристики
Свечение тел, обусловленное нагреванием, называется тепловым излучением. Оно совершается за счет энергии теплового движения атомов и молекул
вещества и свойственно всем телам при температуре выше O K .
Тепловое излучение имеет непрерывный спектр частот, положение максимума которого зависит от температуры тела. Чем выше температура тела, тем
меньше длина волны, на которую приходится максимум излучения.
Тепловое излучение – практически единственный вид излучения, который может быть равновесным. Поместим нагретое тело в изолированную полость, ограниченную идеально отражающей оболочкой. В результате непрерывного обмена энергией между телом и излучением, наступит равновесие, т.е.
тело в единицу времени будет излучать столько энергии, сколько и поглощать и
его температура меняться не будет. При нарушении равновесия в ту или иную
сторону тело будет либо излучать больше (теряет энергию и охлаждается), либо
46
поглощать больше (нагреваться) до тех пор, пока снова не установится равновесие.
Для характеристики любого излучения (в том числе и теплового) вводятся следующие физические величины.
Поток излучения  - величина равная отношению энергии излучения
W ко времени t в течении которого это излучение произошло
W
Дж
6.1

    Вт .
t
с
Излучательность (энергетическая светимость) R - величина равная
отношению потока излучения к площади излучающей поверхности
 W
Вт
6.2
R 
R   2 .
S S t
м
Спектральная плотность излучательности – мощность излучения в интервале частот единичной ширины

dR
R  ,T 
 R   R  ,T  d .
6.3
d
0
Поглощательная способность – какая доля энергии падающей на тело,
поглощается единицей площади поверхности в единицу времени в интервале
частот равном единице
dWпогл
A  ,T 
.
6.4
dWпад
Тело способное полностью поглощать падающее на него излучение при любой температуре
получило название абсолютно черного тела, таким образом, для абсолютно черного тела A,T  1 .
Абсолютно черных тел в природе не существует. Реальной моделью абсолютно черного тела
Рис. 42. Модель абсоможет быть замкнутая полость с малым отверстилютно черного тела
ем, внутренняя поверхность которой зачернена
(Луммер и Вин – 1895 год). Луч света, попавший в
эту полость, многократно отражается от стенок, за счет чего интенсивно поглощается и интенсивность луча, выходящего из отверстия практически равна
нулю (вспомните темные окна домов в яркий летний день). Исследование законов теплового излучения сыграло огромную роль в развитии физики на рубеже 19-20 веков.
2.6.4. Закон Кирхгофа. Универсальная функция Кирхгофа.
В 1809 году Прево сформулировал правило – если два тела поглощают
разное количество теплоты, то и излучение энергии должно быть различным,
т.е. тело, поглощающее больше энергии должно и излучать больше. Другими
словами поглощательная способность тела пропорциональна его излучательной
способности.
47
1859 году Кирхгоф придал правилу Прево вид строго математического
закона, играющего фундаментальную роль во всех вопросах теплового излучения.
Опираясь на второе начало термодинамики и, анализируя условия равновесного излучения в изолированной системе тел, Кирхгоф установил, что отношение спектральной плотности излучательности к спектральной плотности
поглощательной способности не зависит от природы тела и является для всех
тел универсальной функцией частоты и температуры, т.е.
R  ,T
6.5
 r ,T .
A ,T
Для абсолютно черного тела A,T  1 и, следовательно, R ,T  r,T - универсальная функция Кирхгофа есть ничто иное, как спектральная плотность излучательности абсолютно черного тела.
Закон Кирхгофа описывает только тепловое излучение, являясь настолько
характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое не подчиняется закону Кирхгофа,
не является тепловым.
3.6.4. Законы Стефана – Больцмана и смещения Вина.
Закон Кирхгофа ставит в центре внимания теории теплового излучения
универсальную функцию Кирхгофа и поэтому нахождение ее явной зависимости от частоты и температуры являлось важнейшей задачей.
Решение этой задачи было найдено не сразу. В начале был установлен
теоретически и экспериментально подтвержден закон, определяющий суммарное излучение абсолютно черного тела, т.е. его энергетическую светимость R
закон Стефана - Больцмана. Опираясь на законы термодинамики и идею о существовании давления излучения, пропорционального его плотности, Стефан и
Больцман показали, что энергетическая светимость абсолютно черного тела
пропорциональна четвертой степени абсолютной температуры, т.е.
R  T 4 ,
6.6
Вт
где   5,67  108 2 4 - постоянная Стефана – Больцмана. Эксперименм К
тальные исследования Луммера и Вина (1895 г.) и Луммера и Прингсгейма
(1897 г.) подтвердили этот вывод.
Вин, опираясь на законы термодинамики и электродинамики, показал, что
максимум функции r ,T приходится на длину волны, определяемую из закона
b
6.7
 ,
T
где b  2,9 103 м  К - постоянная Вина, а закон получил название закона
смещения Вина.
48
Кроме того, Вин показал, что в максимуме спектральная плотность излучательности абсолютно черного тела пропорциональна пятой степени абсолютной температуры.
4.6.4. Формулы Релея – Джинса, Вина и Планка
Если теоретически осуществить черное тело как совокупность бесконечного числа гармонических осцилляторов, каждый из которых дает отдельную
монохроматическую линию, а все вместе сплошное излучение, то, пользуясь
законами, управляющими поведением таких осцилляторов, можно прийти к законам теплового излучения абсолютно черного тела.
Идя по этому пути, Релей и Джинс получили для универсальной функции
Кирхгофа выражение
2   2
6.8
r ,T 
kT
c2
формула Релея – Джинса.
Как показал опыт, это выражение хорошо согласуется с опытными данными только в области малых частот и резко расходится с ними в области высоких частот. Кроме того, попытка получить закон Стефана – Больцмана на основе этой формулы приводит к абсурдному результату. В самом деле,

R   r ,T  d
6.9
0
и, следовательно, по Релею – Джинсу

2   2
R
k  T  d   .
6.10
c2
0
В то время как по закону Стефана – Больцмана энергетическая светимость абсолютно черного тела имеет конечное значение R    T 4 . Этот вывод
получил название «ультрафиолетовой катастрофы».
В 1896 году Вин для универсальной функции Кирхгофа получил выражение


T
r ,T      e .
6.11
Эта формула хорошо согласуется с опытом в области высоких частот и
резко расходится в области низких.
Таким образом, в рамках классической физики получить выражение для
универсальной функции Кирхгофа не удалось.
М.Планк, анализируя положение, пришел к выводу о том, что причина
неудач лежит в неправильности приложения законов классической физики к
атомным осцилляторам. По классическим законам энергия осциллятора может
принимать любые значения, так как энергия пропорциональна квадрату амплитуды колебания. В соответствии с этим осциллятор может излучать любое количество энергии. По мнению М.Планка эти законы не применимы к атомным
осцилляторам.
3
49
Планк предположил, что атомный осциллятор может иметь энергию пропорциональную частоте колебаний, т.е. E  h , где h - постоянная Планка. В
соответствии с этим и излучение энергии может происходить только порциями,
пропорциональными h . Учитывая новые законы, Планк для универсальной
функции Кирхгофа получил выражение
2   2 h
r ,T 
.
6.12
h
c2
e kT  1
В декабре 1900 года на заседании немецкого физического общества Курльбаум и
Прингсгейм докладывали о новых измерениях спектральной плотности излучательности абсолютно черного тела и посетовали на то, что ни одна из существующих теорий не может
дать правильный результат. Тогда Планк предложил провести расчеты по выведенной им
формуле. Полученное выражение дает полное совпадение с самыми тщательными экспериментальными данными и, следовательно, является полным решением задачи, поставленной
Кирхгофом.
Найдя эту формулу, Планк, чтобы объяснить ее должен был приписать физический
смысл двум константам, которые в ней появились. Для первой константы это было легко. Но
что касается второй, которую Планк назвал «элементарным квантом действия», то это «…
либо фиктивная величина, и тогда весь вывод закона излучения был в принципе ложным и
представлял собой всего лишь пустую игру в формулы, лишенную смысла, либо же вывод
закона излучения опирается на некую физическую реальность, и тогда квант действия должен приобрести фундаментальное значение в физике и означает собой нечто совершенно новое и неслыханное, что должно произвести переворот в нашем физическом мышлении, основывавшемся со времен Лейбница и Ньютона, открывшим дифференциальное исчисление, на
гипотезе непрерывности всех причинных соотношений.»
При низких частотах h  kT и поэтому e
h
kT
1
h 
и формула Планка
k T
переходит в формулу Релея – Джинса.
Легко убедиться в том, что, используя формулу Планка можно получить и
другие законы теплового излучения. При этом оказывается, что постоянные
Стефана – Больцмана и Вина можно выразить через постоянные c,k,h
2 5 k 4
h c

, b
2 3
15c h
4,965  k
и сравнив теоретические и практические значения можно было делать вывод о
справедливости данной теории. Расчеты показали полное совпадение практических и теоретических значений  и b . По известным значениям  и b можно
было найти значение постоянной Планка h .
Это интересно. С математической точки зрения, задача, поставленная Планком, была

достаточно простой. Необходимо было интеграл R 
2   2
0 c2 k  T  d   из расходяще-
гося сделать сходящимся. Иначе обстояло дело с физическим смыслом введенной величины.
4.6.4. Оптическая пирометрия.
Законы теплового излучения используют для определения температуры
раскаленных самосветящихся тел. Методы измерения высоких температур, ис50
пользующие законы теплового излучения, получили название оптической пирометрии. В зависимости от того, какой закон используется для определения
температуры, различают радиационную, цветовую и яркостную температуры.
1. Радиационная температура. В этом случае регистрируется энергетическая светимость тела и по закону Стефана – Больцмана вычисляется темпераR
тура тела T  4 . Радиационная температура Т всегда меньше истинной тем
пературы Ti , так как любое реальное тело является серым телом и для него закон Стефана – Больцмана имеет вид R      T4 , где  - коэффициент серости
R
T
 4 , т.е. Ti  T .
   1 . Тогда Ti  4


2. Цветовая температура. Для серых тел применим закон смещения Вина и поэтому, определяя длину волны, на которую приходится максимум спектральной плотности излучательности тела (цвет излучении) можно по закону
смещения Вина определить температуру тела. Цветовая температура равна истинной температуре тела.
Интересно, что хорошие кузнецы по цвету раскаленной заготовки определяют температуру тела с точностью до 10C . Гремучая змея может определять температуру с точностью до 0,01К.
3. Яркостная температура – температура абсолютно черного тела, при
которой для определенной длины волны спектральная плотность излучательности абсолютно черного тела равна спектральной плотности излучательности
исследуемого тела.
В качестве яркостного пирометра используют пирометр с исчезающей
нитью. Накал нити подбирается таким образом, чтобы на фоне исследуемого
тела изображение нити исчезало. Используя проградуированный по абсолютно
черному телу микроамперметр, можно определить температуру нити. Так как
реальные тела не абсолютно черные, то яркостная температура ниже истинной
температуры.
Задачи к зачету
57. Определить во сколько раз необходимо уменьшить температуру абсолютно
черного тела, чтобы его энергетическая светимость уменьшилась в 16 раз?
кВт
58. Энергетическая светимость абсолютно черного тела 10 2 . Определить
м
длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела.
59. Как надо изменить температуру абсолютно черного тела, чтобы максимум
спектральной плотности излучательности переместился с красной границы
видимого спектра    0,78 мкм  на фиолетовую    0,4 мкм  .
60. Считая никель, абсолютно черным телом, определить мощность, необходимую для поддержания температуры расплавленного никеля 1453С неиз-
51
менной, если площадь его поверхности равна 0,5 см 2 . Потерями энергии
можно пренебречь.
61. Принимая Солнце за абсолютно черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует
длина волны 500 нм, определить температуру поверхности Солнца.
62. Мощность излучения абсолютно черного тела равна 10 кВт. Найти величину излучающей поверхности, если известно, что максимум спектральной
плотности излучения приходится на длину волны 0,7 мкм.
63. Определить как и во сколько раз изменится мощность излучения абсолютно
черного тела. Если длина волны, соответствующая максимуму его спектральной плотности излучения, сместилась с 720 нм до 400 нм.
64. Считая площадь поверхности человеческого тела равной 2 м 2 определить
количество энергии, теряемой человеком в течение суток. Принять температуру окружающей среды равной 20С .
65. Считая человека абсолютно черным телом, определить на какую длину волны приходится максимум спектральной плотности излучательности человека.
66. Мощность излучения шара радиусом 10 см равна 1 кВт. Найти температуру
шара, считая его серым телом с коэффициентом серости 0,25.
67. При какой температуре абсолютно черного тела максимум спектральной
плотности излучательности будет приходиться на длину волны 0,4 мкм?
68. Принимая коэффициент серости угля при температуре 600 К равным 0,8
определить количество энергии излучаемой с поверхности 5 см 2 за 10 мин.
69. Можно условно принять, что Земля излучает как серое тело, находящееся
при температуре 280 К. Определить коэффициент серости Земли, считая, что
кДж
ее энергетическая светимость равна 325 2 .
м ч
70. При увеличении температуры абсолютно черного тела в два раза длина волны, на которую приходится максимум спектральной плотности излучения,
уменьшилась на 400 нм. Определить начальную и конечную температуру
тела.
7.4. Квантовые свойства света.
1.7.4. Явление фотоэффекта и его законы.
Выдвигая идею о прерывистом характере излучения света, Планк считал,
что это лишь удобный математический прием, не имеющий конкретного физического содержания. Тем более что эта идея использовалась лишь для объяснения законов теплового излучения.
Большинство специалистов разделяло мнение Зоммерфельда «Я думаю,
что гипотезу квантов излучения, как и начальную гипотезу квантов энергии,
52
нужно рассматривать скорее как форму объяснения, а не как физическую реальность».
В 1887 году Г.Герц обнаружил, что проскакивание искр в разрядном промежутке значительно облегчается, если их осветить ультрафиолетовым светом
от ртутной лампы или электрической искры.
Систематические исследования Гальвакса, Столетова, Видемана и Эберта
показали, что в опыте Герца дело сводится к освобождению зарядов из электродов под действием света. Попадая в электрическое поле между электродами,
эти заряды ускоряются, ионизируют окружающий газ и вызывают разряд в газе.
Несколько позже было установлено, что под действием света освобождаются отрицательные заряды, а в 1898 году Ленард и Томсон определили удельный заряд частиц и показали, что светом освобождаются электроны.
В первых опытах по наблюдению фотоэффекта использовалось высокое
I
А
V
U
Рис. 44. а) Схема опыта Столетова по изучению фотоэффекта; б) вольт-амперная характеристика фотоэффекта.
напряжение. В 1888 году Столетов решил испытать получится ли подобное
действие при электричестве слабых потенциалов. Схема установки Столетова
приведена на рисунке 44а. Данная установки позволяет исследовать вольтамперную характеристику фотоэффекта – зависимость фототока от приложенного напряжения. Столетов на опыте получил зависимость, показанную на рисунке 44б. Из нее следует, что по мере увеличения напряжения сила тока увеличивается и при некотором значении напряжения достигает насыщения. Пологий характер вольт-амперной характеристики говорит о том, что электроны вылетают из металла с различными скоростями. Из вольт-амперной характеристики следует, что при U  0 сила тока не равна нулю, а это означает, что электроны, выбиваемые светом из катода обладают отличной от нуля кинетической
энергии и могут достигнуть анода в отсутствии электрического поля. Для того
чтобы сила тока стала равной нулю надо приложить некоторое задерживающее
53
напряжение U з . При U  U з ни один из электронов не может преодолеть заmv 2max
 eU з ,
держивающего напряжения, и, следовательно,
2
Таким образом, измеряя задерживающее напряжение, мы можем определить максимальную кинетическую энергию электрона. Наличие тока насыщения говорит о том, что все электроны, вырываемые с поверхности катода, достигают анода.
Путем изучения вольт-амперных характеристик разнообразных материалов при различных частотах падающего излучения были установлены основные
законы фотоэффекта.
1. Число электронов, вырываемых с поверхности металла, пропорционально освещенности катода.
2. Максимальная кинетическая энергия фотоэлектронов пропорциональна частоте падающего излучения.
3. Существует красная граница фотоэффекта, т.е. минимальная частота света, при которой свет любой интенсивности фотоэффекта не
вызывает.
Объяснить законы фотоэффекта на основе волной теории света было невозможно. В самом деле, под действием световой волны в металле возникают
вынужденные колебания электронов, амплитуда которых может быть достаточно большой, достаточной для того, чтобы электрон покинул металл. В этом
случае, энергия электрона должна зависеть от интенсивности света, так как с ее
увеличением электрону передавалась бы большая энергия. На данный вывод
противоречит второму закону фотоэффекта. В рамках волновой теории света
невозможно объяснить существование красной границы фотоэффекта, а также
тот факт, что явление фотоэффекта практически безинерционно.
2.7.4. Уравнение Эйнштейна для фотоэффекта. Фотон.
В 1905 году А.Эйнштейн, воспользовавшись идей Планка о прерывистом
характере излучения света, объяснил законы фотоэффекта. Но Эйнштейн пошел
дальше Планка. Согласно идее Эйнштейна, свет не только излучается отдельными порциями, но и поглощается так же отдельными порциями. Иначе говоря,
излученная порция энергии сохраняет свою индивидуальность до конца, т.е. до
поглощения. По мнению Эйнштейна, явления теплового излучения, фотолюминесценции, фотоэффекта и другие, связанные с возникновением и поглощением
света гораздо лучше объясняются предположением, что энергия распределяется
по пространству дискретно. Энергия пучка света, вышедшего из каждой точки
не распределяется непрерывно во все возрастающем объеме, а складывается из
конечного числа локализованных в пространстве неделимых квантов энергии
поглощаемых или возникающих только целиком.
Если это так, то на основе закона сохранения энергии можно написать
уравнение
54
mv 2
h  A вых 
,
7.1
2
которое полностью объясняет законы фотоэффекта. По мнению Эйнштейна, вся
энергия, приобретаемая электроном, переносится светом в виде порции h , величина которой зависит от частоты колебаний и поглощается целиком. Электрон не заимствует энергию у атома вещества катода, благодаря чему природа
mv 2
 eU з , то уравнение
вещества катода не играет ни какой роли. Так как
2
Эйнштейна можно записать в следующем виде
A  eU з
,
h  A вых  eU з  h  вых

и, следовательно, зная задерживающее напряжение можно рассчитать значение
постоянной Планка.
Планк решительно противился этой гипотезе Эйнштейна. В 1911 году он писал: « Когда думаешь о полном опытном подтверждении, которое получила электродинамика Максвелла при исследовании даже самых сложных явлений интерференции, когда думаешь о
необычайных трудностях, с которыми придется столкнуться всем теориям при объяснении
электрических и магнитных явлений, если они откажутся от этой электродинамики, инстинктивно испытываешь неприязнь ко всякой попытке поколебать ее фундамент. По этой причине мы и далее оставим в стороне гипотезу «световых квантов», тем более что эта гипотеза
находится в зародышевом состоянии.
Будем считать, что все явления, происходящие в пустоте, в точности соответствуют
уравнениям Максвелла и не имеют никакого отношения к константе h ».
Интересно, что, рекомендуя А.Эйнштейна для избрания действительным членом Берлинской академии наук, Планк в своей рекомендации просил не сильно ставить ему в вину
идею о прерывистом характере поглощения света.
В 1916 году Милликен усовершенствовав установку Столетова, экспериментально подтвердил справедливость уравнения Эйнштейна.
В 1928 году П.И.Лукирский применив метод сферического конденсатора
(все электроны достигают поверхности анода) с высокой точностью определил
задерживающее напряжение и рассчитал значение постоянной Планка, которое
совпало со значением, полученным ранее из законов теплового излучения.
Из уравнения Эйнштейна для фотоэффекта следует, что при h  A вых
свет любой интенсивности фотоэффекта вызывать не будет.
Идея о квантовом характере света требовала экспериментального подтверждения. Среди опытов, подтверждающих эту идея следует отметить опыты
Боде и Иоффе и Добронравова.
В опыте Боде тонкая пленка освещалась рентгеновскими лучами и сама
становилась источником рентгеновского излучения. Два счетчика расположенные по обе стороны пленки. Попадание рентгеновского излучения в счетчик
приводит к его срабатыванию и появлению отметки на бумажной ленте. Если
свет волна, то при регистрации волн, излучаемых пленкой счетчики должны
работать синхронно и отметки на ленте должны располагаться друг против друга. Если же излучение происходит порциями, то эта порция может полететь в ту
или иную сторону и показания счетчиков должны быть беспорядочны. Экспе55
риментальные данные говорили о том, что работа счетчиков совершенно хаотична и, следовательно, излучение носит прерывистый характер.
В опытах Иоффе и Добронравова мельчайшие пылинки висмута взвешивались в электрическом поле плоского конденсатора, нижняя пластина которого служила анодом рентгеновской трубки. Анод бомбардировался ускоренными
фотоэлектронами и излучал рентгеновское излучение. Интенсивность бомбардировки подбиралась таким образом, чтобы за 1 секунду излучалось бы 1000
рентгеновских квантов. Опыт говорит о том, что в среднем каждые 30 мин 1
пылинка висмута выходила из состояния равновесия, т.е. рентгеновский квант
вырывал из нее электрон.
Объяснить результаты этого опыта можно только на основе квантовых
представлений. Расчеты показывают, что в пылинку может попасть один из
1800000 квантов, т.е. в среднем в пылинку будет попадать один фотон за 30
мин, что и подтверждается экспериментальными данными.
3.7.4. Эффект Комптона и его объяснение на основе квантовых представлений.
Наиболее полно и ярко корпускулярные свойства света проявляются в
эффекте Комптона. Исследуя рассеяние монохроматического рентгеновского
излучения веществом, Комптон обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдаются и волны
с большей длиной волны. Опыты показали, что изменение длины волны
     не зависит от длины волны падающего излучения и природы рассеивающего вещества, а определяется только величиной угла рассеивания  ,

7.2
  2 с sin 2 ,
2
где c  2,426  1012 м – комптоновская длина волны,  - угол рассеивания.
Эффект Комптона – еще один пример явления, необъяснимого с точки
зрения волновой теории, но получающего очень простое объяснение с помощью теории фотонов, как это вскоре показали Комптон и Дебай.
Математическая теория этого явления, построенная на основе гипотезы
квантов и теории относительности, дает формулу, связывающую угол рассеяния фотона с его начальной и конечной частотой. Более того, когда Комптон
предложил свою теорию, ему еще не удалось на опыте обнаружить электроны
отдачи. Но спустя несколько месяцев Ч.Вильсон и В.Боте экспериментально
наблюдали электроны отдачи. Несколько позже другие исследователи подтвердили, что число электронов отдачи, их энергия и пространственное распределение находятся в полном соответствии с предсказаниями теории.
Объяснение эффекта Комптона было дано на основе квантовых представлений о природе света. Эффект Комптона – это результат упругого столкновения рентгеновских квантов со свободными электронами вещества (вот почему
он не зависит от природы вещества). В процессе этого столкновения квант света передает электрону часть своей энергии и импульса. Как мы знаем в процес56
се упругого взаимодействия выполняются законы сохранения импульса и энергии и, если мы запишем эти законы, то получим:
p0  p  pe
W0  h    W  h  
или
m0c2  h    mc 2  h  
2
2
.
h2
 h   h 

(mv)     

2

cos


c2
 c   c 
Решая совместно эти уравнения и учитывая зависимость массы электрона
от скорости можно получить
h
2h

 
sin 2 .
1  cos   
m 0c
m 0c
2
Полученное выражение есть не что иное, как полученная экспериментально формула Комптона. Таким образом, можно говорить о том, что свет обладает корпускулярными свойствами.
2
4.7.4. Фотон. Масса и импульс фотона. Давление света.
Тепловое излучение и явление фотоэффекта доказывают, что свет обладает корпускулярными свойствами. Массу и импульс фотона (основные характеристики частицы) можно найти следующим образом. Так как энергия фотона
E  h и E  mc2 , тогда
h
h
.
7.3
m 2 
c
c
Так как импульс частицы определяется выражением p  mv , то для фотона
h
h
7.4
p  mc 
c  .
c

Таким образом, для характеристики фотона мы можем ввести характеристики волны  и  , а также энергию E и импульс p – корпускулярные характеристики. Эти характеристики связаны между собой выражениями
h
7.5
E  h, p  .

Если фотоны обладают импульсом, то свет должен оказывать давление на
поверхность, на которую он падает. Величина этого давления определяется по
формуле
E
7.6
p  1    ,
c
где  - коэффициент отражения света, E - энергия света, падающего на
поверхность. Существование светового давления на твердые тела и газы было
доказано П.Н.Лебедевым.
57
Из выражения E  mc2 следует, что масса покоя фотона равна нулю. Это
означает, что фотон может существовать, только двигаясь со скоростью «с».
Задачи к зачету
71. Красная граница фотоэффекта для некоторого металла равна 400 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект.
72. Калий освещается светом с длиной волны 400 нм. Определить минимальное
задерживающее напряжение, при котором фототок прекращается. Работа
выхода электронов из калия равна 2,2 эВ.
73. Определить работу выхода электронов из вольфрама, если красная граница
фотоэффекта для него равна 275 нм.
74. Будет ли наблюдаться фотоэффект, если на поверхность серебра направить
излучение с длиной волны 300 нм? Работа выхода электронов из серебра
равна 4,7 эВ.
75. Красная граница фотоэффекта для металла равна 500 нм. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности излучением с длиной волны 400 нм.
76. Выбиваемые светом с длиной волны 400 нм из катода электроны полностью
задерживаются напряжением 1,2 В. Определить красную границу фотоэффекта.
77. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности цинка (работа выхода 4 эВ), излучением с длиной волны 247 нм.
78. Определить длину волны рентгеновского излучения, если при комптоновском рассеянии этого излучения под углом 60 длина волны рассеянного
излучения оказалась равной 57 пм.
79. Фотон с энергией 0,3 МэВ рассеялся под углом 180 на свободном электроне. Определить долю энергии фотона, приходящуюся на рассеянный фотон.
80. Фотон с энергией 0,4 МэВ рассеялся под углом 90 на свободном электроне. Определить энергию рассеянного фотона и кинетическую энергию
электрона отдачи.
81. Фотон с энергией 1,025 МэВ рассеялся на первоначально покоившемся
электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона стала равна 2,43 пм.
82. Фотон с энергией 0,25 МэВ рассеялся на свободном электроне на угол 120 .
Определить кинетическую энергию электрона отдачи.
83. Фотон с длиной волны 5 пм испытал рассеяние под углом 90 на первоначально покоящемся свободном электроне. Определить: изменение длины
волны фотона; энергию электрона отдачи; импульс электрона отдачи.
84. Угол рассеяния фотона 90 . Угол отдачи электрона 30 . Определить энергию падающего фотона.
58
8.4. Теория атома водорода.
1.8.4. Спектр атома водорода
Одним из важнейших вопросов в оптике был вопрос об излучении энергии атомом. И здесь мы, прежде всего, должны обратиться к области оптики
занимающейся изучением спектров. Детальное изучение спектров показало, что
атом излучает и поглощает одни и те же длины волн. Почему? Почему спектры
атомов являются линейчатыми? Почему все химические элементы имеют различные спектры?
Наиболее изученным оказался спектр атома водорода, самого простого
атома.
Бальмер подобрал эмпирическую формулу, описывающую все известные
к тому времени спектральные линии в видимой части спектра атома водорода
1
1 1 
 R  2  2  где n  3,4,5,..... , а R - постоянная Ридберга.

2 n 
В дальнейшем в спектре атома водорода были обнаружены еще несколько серий, описываемых формулами
1
1 1 
 R  2  2  , где n  2,3,4,.... Серия Лаймана – ультрафиолет

1 n 
1
1 1 
 R  2  2  , где n  4,5,6,...... Серия Пашена – инфракрасная

3 n 
1
1 1 
 R  2  2  , где n  5,6,7,.... Серия Брекета – инфракрасная и др.

4 n 
Все эти серии могут быть описаны одной формулой вида
1
1 
 1
 R 2  2 ,

m n 
где n имеет постоянное значение, а m принимает значения
n  1, n  2, n  3,....... .
Приведенные выше формулы были подобраны эмпирически и долгое
время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень высокой точностью.
2.8.4. Атом водорода по Бору.
После открытия Томсоном электрона стало ясно, что атом имеет сложное
строение.
Совокупность сведений об оптических явлениях, свидетельствует о том,
что излучение света обусловлено процессами, в которых принимают участие
электроны, входящие в состав атома.
59
Для объяснения линейчатого спектра атома, следовало предположить, что
электрон в атоме совершает гармонические колебания, которые и обуславливают монохроматическое излучение.
Опираясь на закон Кулона и законы движения гармонического осциллятора, Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненную положительным зарядом сферу, в которую
вкраплены электроны.
Модель Томсона не опиралась на эксперимент и поэтому важнейшим шагом можно считать попытки непосредственного опытного зондирования внутренних областей атома с целью установления пространственного распределения электрического заряда в атоме.
В 1903 году Нагаока предложил модель атома, о которой он писал: «Очевидно, что такая система будет приближенно реализована, если мы электроны
разместим по кольцу, а положительный заряд в центре. Такой атом не будет
противоречить результатам недавних опытов с катодными лучами, радиоактивностью и другими связанными с этим явлениями».
Наиболее успешная попытка зондирования атома была предпринята Резерфордом в 1907 -1913 годах. Пользуясь возможностью наблюдения отдельных  - частиц, Резерфорд исследовал, каким образом меняется направление
полета частиц при прохождении через слой какого-либо вещества.
При прохождении  - частицы через вещество происходит изменение
направления ее полета в результате взаимодействия с зарядами, входящими в
состав атома. При этом столкновение с электронами не может существенно повлиять на изменение направления движения, так как масса электрона почти в
8000 раз меньше массы  - частицы. Напротив, столкновение с положительно
заряженной частью атома может вызвать более или менее резкое изменение
направления движения  - частицы.
Опыт показал, что приблизительно одна из 5000 частиц испытывает отклонение на угол, больший 180 , т.е. поворачивает обратно. Для объяснения
этого факта приходится предположить, что довольно часто происходят столкновения, вызывающие сразу крутой поворот  - частицы.
Объясняя результаты опыта по рассеиванию  - частиц Резерфорд предложил планетарную модель атома, согласно которой в центре атома находится положительно заряженное ядро, в котором сосредоточена вся масса атома.
Вокруг ядра вращаются электроны. Так как атом в целом нейтрален, то суммарный заряд электронов равен заряду ядра.
Для простоты рассуждений предположим, что электрон в атоме водорода
движется по круговой орбите. В этом случае, второй закон Ньютона для электрона запишется в виде
m  v2
1 e2
1 e2
2
.
8.1

 mv 
r
40 r 2
40 r
Полученное выражение содержит две неизвестные величины r и v , а
из курса математики известно, что одно уравнение с двумя неизвестными имеет
множество решений. Следовательно, существует множество значений радиуса
60
и соответствующих ему значений скорости (а значит и энергии), удовлетворяющих этому уравнению. Иными слова, r, v и E могут меняться непрерывно и
при переходе с одной орбиты на другую, может испускаться любая порция
энергии. Чего на опыте не наблюдается.
Кроме того, планетарная модель атома оказалась электродинамически неустойчивой. Согласно законам электродинамики, движущаяся с ускорением заряженная частица должна излучать энергию и вследствие этого электрон должен терять энергию и приближаться к ядру. Как показали расчеты, за время порядка 108 с, электрон должен упасть на ядро и атом прекратить свое существование, что опять таки противоречит опыту. Итак, по законам классической физики атом должен быть неустойчив и в течение времени существования должен
излучать непрерывный спектр. Оба этих вывода стоят в резком противоречии с
опытом.
Таким образом, построение модели атома в рамках классической физики
оказалось невозможным.
В 1913 году Бор предпринял первую попытку построения квантовой модели атома, в которой он попытался объединить планетарную модель атома,
спектральные закономерности и гипотезу Планка. В основу своей теории он
положил два постулата.
1. Атомная система может находиться только в определенных стационарных состояниях. Каждому стационарному состоянию соответствует
определенное значение энергии E n . Находясь в стационарном состоянии,
атом не излучает энергии.
По Бору условие квантования имеет вид
8.2
mvr  n  .
Решая совместно два уравнения
mvr  n
1 e2
 m  v2
4 0 r
найдем, что r 
8.3
n
и для скорости движения электрона получаем следующее
mv
выражение
e2
.
8.4
v
4   0  n 
Радиус электронной орбиты будет определяться выражением
2
2 4   0 
.
8.5
rn  n 
m  e2
Для
первой
электронной
орбиты
получается
значение
2
40
a  r1 
 0,5  1010 м - Боровский радиус или размер атома. Это значение
2
me
хорошо согласуется с данными о размерах атома, полученными другими методами.
61
2. Излучение и поглощение энергии атомом происходит при переходе
системы из одного стационарного состояния в другое и при этом излучается (поглощается) квант энергии равный разности энергий стационарных
состояний h  E m  E n .
Зная скорость электрона и радиус электронной орбиты, мы можем определить полную энергию электрона в атоме водорода
1 e2 mv2
1 me4
8.6
En  

 2 2 2 .
40 r
2
n 8 0
И тогда согласно второму постулату Бора
me4  1
1 
1 
 1
8.7
h  E n  E m  2 2  2  2   R  2  2  ,
8 0  m n 
m
n


4
me
где R  2 2 - постоянная Ридберга. Тот факт, что расчетное значение посто8h 0
янной Ридберга совпадает с экспериментальными данными, полученными из
спектроскопических измерений, говорит о справедливости полученной Бором
формулы.
Теория Бора позволила объяснить возникновение серий в спектре атома
водорода. Так серия Бальмера возникает при переходе электрона из возбужденного состояния на второй энергетический уровень, а серия Лаймана на первый
уровень.
Спектр поглощения атома водорода, содержащий только серию Лаймана,
также объясняется теорией Бора. Так как свободные атомы находятся в основном состоянии (с наименьшим значением энергии), то при поглощении света
они могут переходить только из основного состояния в возбужденное.
Теория Бора стала крупным шагом в развитии квантовой теории. Однако
она была внутренне противоречивой, так как в ней была предпринята попытка
соединить классические законы и законы квантовой механики. Поэтому в рамках этой теории не удалось описать спектры более сложных атомов.
3.8.4. Рентгеновское излучение.
В 1895 году В.Рентгеном было открыто излучение, получившее название
рентгеновского. Оно представляет собой электромагнитное излучение с длиной волны порядка 108  1010 м . Источником рентгеновского излучения является рентгеновская трубка, в которой ускоренные до больших значений энергии
электроны, бомбардируют анод (металлическая мишень из тяжелых металлов),
испытывая на нем резкое торможение.
Исследование спектрального состава рентгеновского излучения показало,
что его спектр имеет сложную структуру. Он представляет собой наложение
сплошного спектра, ограниченного со стороны коротких волн некоторой границей  m и линейчатого спектра – совокупности отдельных очень резких линий, появляющихся на фоне сплошного спектра. Характер сплошного спектра
совершенно не зависит от материала анода, а определяется только энергией
62
электронов, бомбардирующих анод. Исследования показали, что оно испускается электронами в результате их торможения при столкновении с анодом и поэтому, сплошной рентгеновский спектр получил название тормозного спектра.
Наличие коротковолновой границы спектра подтверждает справедливость
квантовой теории. Предельная энергия рентгеновского кванта соответствует
тому случаю, когда вся кинетическая энергия электрона переходит в энергию
кванта, т.е.
mv2 hc
mv2
hc
.
8.8

,
 eU   m 
2
m
2
eU
Измеряя границу рентгеновского спектра  m по данной формуле можно
вычислить значение постоянной Планка h .
При увеличении кинетической энергии электронов (увеличение напряжения на электродах трубки) наряду со сплошным возникает линейчатый спектр,
зависящий от материала анода и называемый характеристическим спектром.
По сравнению с оптическими спектрами химических элементов (они самые разнообразные) рентгеновские спектры совершенно однотипны и состоят
из нескольких серий, обозначаемых K,L,M, N,O . Каждая серия состоит из нескольких линий. При переходе от легких
элементов к тяжелым структура спектра не
меняется, лишь весь спектр смещается в стоM
рону более коротких волн. Особенность этих
L
спектров состоит в том, что атомы каждого
L
элемента, независимо от того свободны они
или входят в состав химического соединения
K
обладают определенным характерным для
K
данного элемента линейчатым спектром.
Рис. 45. Образование характериИзучение структуры характеристичестического рентгеновского спектра
ских рентгеновских спектров приводит нас к
выводу о том, что их возникновение связано с процессами, происходящими во
внутренних заполненных электронных оболочках атомов, которые имею сходное строение.
Под действием кого-нибудь внешнего фактора электрон с оболочки К
может перейти на более высокую оболочку, а в К-оболочке возникает вакансия,
куда может перейти электрон с другой оболочки, излучая при этом рентгеновский квант.
Мозли установил, что частоту линий в характеристическом рентгеновском спектре можно определить по формуле, аналогичной сериальной формуле
для атома водорода
1 
 1
   Z    R  2  2  ,
8.9
m 
n
где Z - порядковый номер элемента в таблице Менделеева,  - постоянная экранирования.
63
4.8.4. Поглощение, спонтанное и вынужденное излучение. Лазеры.
Если атом находится в основном состоянии, то под действием внешнего
излучения может осуществить вынужденный переход в возбужденное состояние.
Находясь в возбужденном состоянии, атом может самопроизвольно
(спонтанно) без каких-либо внешних воздействий, перейти в основное состояние, отдавая избыточную энергию виде кванта электромагнитного излучения.
Процесс излучения света возбужденным атомом без каких-либо внешних воздействий получил название спонтанного излучения.
В 1916 году А.Эйнштейн для объяснения равновесного характера теплового излучения предположил, что кроме спонтанного, должен существовать и
качественно иной характер излучения. Если на атом, находящийся в возбужденном состоянии, действует внешнее излучение с частотой, удовлетворяющей
равенству h  E 2  E1 , то возникает вынужденный переход в основное состояние с излучением фотона той же энергии. Возникающее в таких переходах излучение получило название вынужденного излучения. В процесс вынужденного излучения вовлечены два фотона – первичный, вызывающий излучение, и
вторичный фотон, испущенный атомом. Существенно, что вторичный фотон не
отличается от первичного, являясь его точной копией.
В статистической физике известен принцип детального равновесия, согласно которому при термодинамическом равновесии каждому процессу в системе можно сопоставить обратный процесс, при этом скорость их протекания
будет одинаковой.
Применяя этот принцип и закон сохранения энергии для излучения и поглощения
энергии, в случае абсолютно черного тела А.Эйнштейн получил формулу Планка.
Испущенные фотоны, двигаясь в одном направлении и встречая на своем
пути другие возбужденные атомы, стимулируют дальнейшее вынужденное излучение, и число фотонов растет лавинообразно.
В 1918 году А.Эйнштейн указал на возможность усиления света с помощью вынужденного излучения. Для усиления падающего излучения необходимо, чтобы число актов вынужденного излучения превышало бы число актов поглощения. Для выполнения этого условия систему надо перевести в неравновесное состояние, при котором число атомов в возбужденном состоянии было
больше, чем их число в основном состоянии. Процесс создания неравновесного
состояния вещества называется накачкой.
Впервые на возможность получения сред, в которых может происходить
усиление света за счет вынужденного излучения, в 1940 году указал Фабрикант,
который вместе с сотрудниками в 1951 году изобрел способ усиления света за
счет вынужденного излучения.
Практически усиление света осуществляется в принципиально новых источниках света – лазерах. Идея качественно нового принципа усиления света
64
принадлежит Н.Г.Басову, А.М.Прохорову и Ч.Таунсу которые в 1964 году получили Нобелевскую премию по физике.
В основе работы лазера лежит так называемая трехуровневая схема (рис.
46). При накачке электроны из основного состояния пе2
реходят в возбужденное состояние 2. Из этого состоя3 ния без излучения энергии электроны переходят на метастабильный уровень 3. Самопроизвольный переход
3  1 запрещен правилами отбора и поэтому в этом со1
стоянии электрон может находиться в течение достаточно большого промежутка времени до 103 c  (сравРис. 46. Трехуровневая
схема лазера
ните с 108 c при спонтанном излучении).
Это приводит к тому, что происходит накопление электронов на этом
уровне. При достаточной мощности накачки на уровне 3 электронов будет гораздо больше, чем в основном состоянии.
Фотон с энергией h  E 3  E1 , случайно появившейся в среде, вызывает
множество актов вынужденного перехода 3  1, в результате чего зарождается
лавина фотонов. Но эти фотоны разлетаются в различных направлениях.
Чтобы выделить определенное направление, в котором испускаются фотоны, используют оптический резонатор. В простейшем случае им служат два
обращенных друг к другу зеркала на общей оптической оси. Для формирования
пучка одно из них делается полупрозрачным.
В первых моделях лазеров в качестве активной среды использовался цилиндрический столбик из рубина, торцевые поверхности которого тщательно
обрабатывались и серебрились.
Лазерное излучение обладает следующими свойствами:
- высокая когерентность;
- строгая монохроматичность;
- большая мощность излучения;
- малый угол расхождения.
Необычные свойства лазерного излучения находят широкое применение в
самых различных областях науки и техники.
9.4. Элементы квантовой механики.
1.9.4. Корпускулярно - волной дуализм.
На протяжении всей своей истории физика не раз оказывалась в ситуации, когда общепринятая теория не могла объяснить целого ряда явлений. Но
всегда находился выход – создавалась новая теория, более общая, способная
объяснить и старые, и новые факты.
Но в данном случае ситуация была несколько иная – новая теория квантов не представлялась более общей, чем волновая, в том смысле, что некоторые
явления объясняемые квантовой теорией невозможно объяснить с точки зрения
65
волновой теории и наоборот. Противоречие волна – частица казалось неразрешимым.
Экспериментально подтверждение корпускулярно-волнового дуализма
для света позволило Луи де Бройлю в 1924 году выдвинуть гипотезу об универсальном характере этого явления. Де Бройль утверждает, что не только свет, но
и другие частицы материи наряду с корпускулярными свойствами обладают
также и волновыми свойствами.
По де Бройлю любой микрообъект можно характеризовать энергией и
импульсом (корпускулярные свойства), а другой стороны – частотой и длиной
волны (волновые свойства). Количественные соотношения, связывающие эти
характеристики, такие же, как и у света, т.е.
h
9.1
E  h, p  .

Смелость гипотезы де Бройля состояло в том, что данные соотношения
постулировались не только для света, но и для других объектов микромира, в
том числе и для таких которые обладают массой покоя. Из гипотезы де Бройля
следует, что любой частице, обладающей импульсом « р » мы можем сопоставить волну, длина которой определяется выражением
h
9.2

p
и называется длиной волны де Бройля.
В 1927 году гипотеза де Бройля получила экспериментальное подтверждение. Джермер и Девисон на опыте наблюдали дифракцию электронов при
рассеивании на естественной дифракционной решетке, кристалле никеля. По
распределению максимумов и минимумов в дифракционной картине можно
было определить длину волны. Экспериментальные данные подтвердили гипотезу де – Бройля. Несколько позже дифракционные явления были обнаружены
у нейтронов, протонов и других микрочастиц.
Открытие волновых свойств у частиц привело к возникновению новых
методов исследования структуры вещества – электронной микроскопии,
нейтронографии и других методов.
Экспериментально подтверждение гипотезы де Бройля показало, что перед нами универсальное свойство материи.
Но тогда возникает вопрос, почему мы не наблюдаем волновых свойств у
человека? Расчет показывает, что для человека массой 60 кг, движущегося со
м
6,62 1034
скоростью 1 длина волны де – Бройля  D 
 1,1  1035 м. Обнарус
60 1
жить эту волну мы не можем, так как в природе периодических структур с таким периодом не существует.
Экспериментальное подтверждение гипотезы де Бройля коренным образом изменило наши представления о микрообъектах.
Всем микрообъектам присущи и волновые, и корпускулярные свойства,
но в то же время любую из частиц нельзя считать ни частей, ни волной в классическом понимании этого слова.
66
Это интересно. Опираясь на свою идею о волнах материи, де Бройль выводит формулу Планка E  h .
2.9.4. Соотношение неопределенностей Гейзенберга
Двойственная природа частиц вещества, вынуждающая описывать микрочастицы как с помощью корпускулярных, так и волновых представлений,
ставит вопрос о границах применимости понятий классической физики к объектам микромира.
В классической физике всякая частица движется по определенной траектории, так, что в любой момент времени точно определены ее координата и импульс.
Одно из основных отличий микрочастиц заключается в том, что она не
имеет траектории и неправомерно говорить о точном значении ее координаты и
импульса. В самом деле, понятие длины волны в данной точке не имеет смысла.
В 1927 году Гейзенберг, учитывая волновые свойства частиц и накладываемые этим ограничения, пришел к выводу о том, что объект микромира невозможно одновременно с одинаковой степенью точности охарактеризовать его
координатой и импульсом. По Гейзенбергу, неопределенности в значениях этих
величин удовлетворяют неравенству
x  p x  h 9.3
соотношение неопределенностей Гейзенберга.
Отсюда следует, что в случае если мы точно знаем положение частицы
( x  0 ), ее импульс совершенно не определен  p x    и наоборот.
Невозможность одновременно точно определить координату и импульс
частицы ни коим образом не связана с несовершенством методов измерения
или измерительных приборов. Она является результатом специфики микрообъектов, отражающей особенности их объективных свойств.
Так как в классической физике принимается, что измерение координаты и
импульса может быть произведено с любой точностью, то соотношение неопределенностей Гейзенберга является, таким образом, квантовым ограничением применимости законов классической механики к объектам микромира. Рассмотрим некоторые примеры. Преобразуем соотношение неопределенностей,
так как p x  m  v x , то
h
9.4
x  v x  .
m
Рассмотрим движение электрона в кинескопе телевизора. Пусть скорость
движения электрона 107 м с , определена с точность до 1%, т.е. v  105 м с .
6,62 1034
Тогда неопределенность координаты электрона x 
 7  108 м
31
5
9 10 10
значительно меньше толщины пучка электронов и ею можно пренебречь. Таким образом, при расчете кинескопа телевизора электроны можно считать
классическими частицами.
Рассмотрим движение электрона в атоме. Пусть неопределенность координаты электрона равна х  1010 м (электрон принадлежит атому). Тогда не67
6,62 1034
определенность скорости электрона v 
 7  106 м с . Расчет пока31
10
9 10 10
зывает, что в атоме электрон движется со скоростью 2  106 м с , другими словами, неопределенность определения скорости в 3 раза превышает само значение
скорости. Следовательно, электрон в атоме нельзя считать классической частицей.
Каким же образом для представления такой величины как электрон, могут быть использованы без противоречия две столь различные между собой модели – корпускулярная и волновая. Н. Бор показал, что из-за соотношения
неопреленностей эти модели никогда не могут войти в противоречие друг с
другом, потому что чем больше уточняется одна модель, тем более неопределенной становится вторая. Оба этих аспекта – волновой и корпускулярный – не
приходят в столкновение, потому что никогда не предстают одновременно. Чем
более четкими оказываются в каком-либо явлении корпускулярные свойства,
тем более незаметными и неясными оказываются его волновые свойства. Таким
образом, электрону присущи два аспекта, и он предстает то в одном из них, то в
другом, но никогда не предстает одновременно в обоих.
3.9.4. Волновая функция и ее статистический смысл.
Экспериментальное подтверждение гипотезы де Бройля поставило перед
специалистами новые проблемы. В частности необходимо было истолковать
физическую природу волн де Бройля.
Для выяснения природы волн де Бройля сравним дифракцию света и частиц. Согласно волновым представлениям о природе света интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны,
но с точки зрения корпускулярной теории – интенсивность картины определяется числом фотонов, попадающих в данную точку дифракционной картины.
Следовательно, число фотонов в данной точке определяется квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды
световой волны определяет вероятность попадания фотона в ту или иную точку
пространства.
Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков частиц. В одних направлениях
наблюдается большее количество частиц, в других меньшее. В максимуме дифракционной картины – наибольшее количество частиц и наибольшая интенсивность волн де Бройля. Таким образом, дифракционная картина для микрочастиц является отражением статистической (вероятностной) закономерности, согласно которой частицы попадают в те точки, где интенсивность волн де –
Бройля наибольшая.
Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой механики.
Волны де Бройля нельзя истолковывать как волны вероятности (вероятность не может быть отрицательной). Поэтому М.Борн предположил, что по
68
волновому закону меняется не сама вероятность, а некая величина названная
амплитудой вероятности   x, y,z, t  или пси – функцией, или волновой
функцией. Вероятность обнаружить частицу в той или иной точке пространства определяется квадратом волновой функции, т.е.
dW    x, y,z, t   dV .
2
9.5
4.9.4. Уравнение Шредингера.
Необходимость применения статистического метода привело к выводу о
том, что уравнение движения в квантовой механике, описывающее движение
микрочастиц во внешних силовых полях, должно быть уравнением, из которого
бы вытекали наблюдаемые на опыте волновые свойства частиц. Очевидно, что
это уравнение должно быть уравнением относительно волновой функции
  x, y,z, t  , так как именно она определяет вероятность обнаружения частицы в
объеме dV в данный момент времени. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением.
Следует отметить, что это уравнение не выводится, а постулируется (подобно второму закону Ньютона или уравнениям Максвелла). В 1926 году Шредингер нашел вид этого уравнения

,
9.6

  U  x, y,z, t     i  
2m
t
где  - волновая функция, U  x, y,z, t  - потенциальная энергия частицы.
Это уравнение называется общим уравнением Шредингера.
Для многих физических процессов, происходящих в микромире это уравнение можно упростить, исключив из него зависимость  от времени t . Это
возможно в том случае, если силовое поле стационарно, т.е. функция
U  x, y,z, t  не зависит явно от времени и имеет смысл потенциальной энергии
U  x, y,z  . В этом случае уравнение Шредингера будет иметь вид
2m
9.7
  2  E  U     0
и называется уравнением Шредингера для стационарных состояний. В это
уравнение в качестве параметра входит полная энергия частицы Е. В теории
дифференциальных уравнений доказывается, что это уравнение имеет решение
лишь при определенных значениях параметра Е, которые получили название
собственных значений энергии. Собственные значения энергии могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о
непрерывном спектре, во втором – о дискретном. В качестве примера рассмотрим движение свободной частицы.
При движении свободной частицы ее потенциальная энергия равна нулю и полная энергия совпадает с кинетической энергией. Для свободной частицы, движущейся вдоль оси Х, уравнение Шредингера будет иметь вид:
69
 2 2m

 E   0.
x 2
Прямой подстановкой можно убедиться в том, что частным решением
этого уравнения является функция
  Acos   t  kx  ,
 2
2mE
где A  const и k 2 
. Так как k  
и, учитывая, что длина волны
v 
p 2 2mE
2p p
h

де Бройля   , то будем иметь k 
 . Следовательно, 2  2
h
p
p  2mE - из полученного выражения следует, что зависимость энергии от
импульса оказывается обычной для нерелятивистской частицы и для ее энергии
k2  2
получается выражение E 
. Из этого выражения следует, что энергия
2m
свободной частицы может принимать произвольные значения.
5.9.4. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.
Пусть частица находится в одномерной прямоугольной потенциальной
яме бесконечной глубины шириной и имеет возможность двигаться вдоль
оси Х. Тогда потенциальная энергия частицы будет иметь значение
  , x  0

U  x   0, 0  x  .
9.8
  , x 

В данном одномерном случае уравнение Шредингера примет вид
d 2 2m
9.9

E  U    0 .
dx 2
По условию частица не может покинуть ямы и поэтому   0       0 ,
т.е. вероятность обнаружения частицы за пределами ямы равна нулю. В пределах ямы U  x   0 и поэтому уравнение Шредингера можно преобразовать к
виду
d 2 2mE
или

0
dx 2
d 2
9.10
 k 2  0 ,
2
dx
2mE
где k 2  2 .
Решение этого уравнения ищется в виде   x   Asin kx  Bcos kx . Из
условия   0   0 получим:
70
  x   Asin kx .
0  Asin kx  Bcos kx  B  0 и тогда
Условие     0 выполняется, если k  n   , где n  0,1,2,....... . Отсюда
для собственных значений энергии получаются значения
n 2  2  2
,
9.11
E
2m  2
т.е. энергия частицы находящейся в потенциальной яме не может принимать
произвольные значения, а квантуется.
Теперь мы можем получить волновую функцию частицы в потенциальной яме
n
9.12
  x   Asin(
 x) .
Из условия нормировки
 x
2
dx  1 можно получить, что A 
2
и,
следовательно, волновая функция частицы имеет вид
2  n 
9.13
x 
sin  x  .


n 2  2  2
Из выражения E 
следует, что энергетический интервал между
2m  2
двумя состояниями
2  2
E n 1  E n 
 2n  1 .
2m 
В качестве примера рассмотрим два случая. Свободные электроны в металле, ширина потенциальной ямы  0,01 м и тогда
10 1068
E 
2n  1  5 1035  2n  1 Дж ,
31
2 
2  9 10 10
т.е. энергетические уровни расположены столь густо, что можно говорить о
сплошном спектре.
Для электрона в атоме ширина потенциальной ямы имеет величину порядка 1010 м и тогда для Е получим значение
1067
E 
2n  1  5  1017  2n  1 Дж,
50 
1,8  10
Рис. 47. Графики собственных
функций плотности вероятности
обнаружения частицы
т.е. явно квантуется.
Квантово механическое решение задачи о движении частицы в потенциальной яме,
приводит к тому, что она не может иметь
2  2
энергию меньшую, чем E1 
.
2m 
Графики собственных функций, соответствующие различным значениям n , при71
ведены на рисунке. Слева изображена плотность вероятности обнаружения частицы в той или иной части ямы. Из рисунка следует, что в состоянии с n  2 ,
вероятность обнаружить частицу в центре ямы равна нулю, в то время как одинаково часто мы можем обнаружить частицу в одной и половинок ямы.
5.9.4. Гармонический осциллятор в квантовой механике.
Потенциальная энергия гармонического осциллятора определяется выраm  02  x 2
жением U 
. Эта зависимость имеет вид параболы, т.е. «потенциаль2
ная яма» в данном случае является параболической.
Гармонический осциллятор в классической механике описывается уравнением x  02  x  0 и, следовательно, его энергия может принимать любые
значения, те. Спектр является сплошным.
В квантовой механике осциллятор описывается уравнением Шредингера
 2 2m 
m  02  x 2 

E 
  0,
x 2
2


где Е – полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что это уравнение имеет решение только при собственных
1

значениях энергии E   n    0 . Из этого выражения следует, что энергия
2

квантового осциллятора квантуется, т.е. может принимать только дискретные
значения.
6.9.4. Атом водорода в квантовой механике.
Решение задачи об энергетических уровнях электрона в атоме водорода
сводится к решению задачи о движении электрона в кулоновском поле ядра.
Потенциальная энергия взаимодействия электрона с ядром определяется
выражением
e2
.
U
4   0  r
Следовательно, состояние электрона в атоме водорода описывается
функцией  , удовлетворяющей уравнению Шредингера в виде

2m 
e2
  2  E 
  0.
4




r
0


Мы уже указывали, что подобное дифференциальное уравнение имеет
решение только при определенных значениях параметра Е. Как показывают
расчеты
1 me4
En   2 2 2 .
n 8h 0
72
Легко заметить, что полученное решение совпадает со значением полученным Бором, но Бор вынужден был вводить дополнительные гипотезы, а в
квантовой механике это результат самой теории, вытекающий из решения
уравнения Шредингера.
Задачи к зачету
85. Электрон движется со скоростью 2  108 м с . Определить длину волны де
Бройля для электрона, учитывая зависимость массы от скорости.
86. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы
длина волны де Бройля была равна 0,1 нм?
87. Найти длину волны де Бройля протона, прошедшего ускоряющую разность
потенциалов 1 МВ.
88. Предполагая, что неопределенность координаты движущейся частицы равна
дебройлеровской длине волны, определить относительную неопределенр
ность
импульса частицы.
р
89. Электрон находится в потенциальной яме шириной в возбужденном состоянии  n  2  . Определить в каких точках интервала  0  x   плотность
вероятности нахождения частицы минимальна?
90. Электрон находится в потенциальной яме шириной в возбужденном состоянии  n  2  . Определить в каких точках интервала  0  x   плотность
вероятности нахождения частицы максимальна?
91. Электрон в одномерной потенциальной яме шириной
находится в возбужденном состоянии  n  2  . Определить вероятность обнаружения части3
5
цы в области
x .
8
8
92. Электрон в одномерной потенциальной яме шириной
находится в возбужденном состоянии  n  3 . Определить вероятность обнаружения части1
2
цы в области
.
x
3
3
10.4. Элементы физики атомного ядра.
1.10.4. Открытие нейтрона. Строение атомного ядра.
В 1920 году Э.Резерфорд в камере Вильсона наблюдал первую ядерную
реакцию
4
14
17
1
10.1
2 He  7 N  8 O  1 H
в результате которой образовывался протон.
В 1930 году В.Боде и Г. Беккер облучая ряд элементов обнаружили, что
при облучении бериллия  - частицами возникает излучение большой проникающей способности, но не оставляющей следов в камере Вильсона. Так как
большой проникающей способностью могут обладать только нейтральные ча73
стицы, то было высказано предположение о том, что это кванты электромагнитного излучения. Однако измерение энергии  - квантов проведенное Ирен и
Фредериком Жолио-Кюри показало, что они должны были обладать невероятной энергией, порядка 50 МэВ, вместо расчетных 7 Мэв.
В 1932 году Д.Чедвик вначале предположил, а затем и доказал, что при
бомбардировке бериллия образуются нейтральные частицы, которые он назвал
нейтронами. Таким образом, при бомбардировке бериллия протекает ядерная
реакция
9
4
12
1
10.2
4 Be  2 He  6 C  0 n .
По своим характеристикам (кроме электрического заряда) нейтрон подобен протону и поэтому для этих частиц используется общее название нуклон.
Открытие нейтрона позволило Д.И.Иваненко и Гейзенбергу высказать
гипотезу о строении атомного ядра. Так как заряд ядра равен Z ( Z - атомный
номер элемента), то в его состав должно входить Z протонов и число нейтронов равное N  A  Z (А – массовое число, число нуклонов в ядре).
Поскольку нейтроны не участвуют в электромагнитном взаимодействии,
а протоны отталкиваются друг от друга, то необходимо было ответить на вопрос о стабильности ядра.
В ядре между нуклонами действуют особые, специфические силы, называемые ядерными силами. Закон ядерных сил не установлен, но установлены
их основные свойства:
- ядерные силы являются силами притяжения;
- эти силы являются короткодействующими – радиус действия  1015 м ;
- ядерным силам свойственна зарядовая независимость (действуют между
протонами и нейтронами);
- им свойственно насыщение, т.е. каждая частица может взаимодействовать с определенным числом соседей;
- ядерные силы не являются центральными.
Сложный характер ядерных сил, трудность решения уравнений движения
нуклонов в ядре не позволяют разработать единую теорию атомного ядра. И
поэтому в настоящее время прибегают к рассмотрению приближенных моделей
ядра. Наиболее известны из них капельная и оболочечная.
1. Капельная модель (Я.И.Френкель, Н.Бор). Эта модель основана на
аналогии между поведением нуклонов в ядре и молекул в капельке жидкости.
Силы, действующие между молекулами в жидкости (силы поверхностного
натяжения) и ядерные силы обладают сходными свойствами (не являются центральными, для них характерно насыщение). Объем капли и ядра зависит от
числа частиц. Плотность капли жидкости и плотность ядра остаются величинами постоянными.
В рамках этой модели удалось получить полуэмпирическую формулу для
энергии связи ядра и объяснить механизм деления ядер.
2. Оболочечная модель. В данной модели нуклоны ядра располагаются
по оболочкам (подобно электронам в атоме) с дискретными значениями энергии. Устойчивость ядра зависит от степени заполнения оболочек. Ядра с полно74
стью заполненными оболочками наиболее устойчивы. Магические числа – 2, 8,
20, 28, 50, 82, 126. Ядра, содержащие это число протонов или нейтронов,
наиболее устойчивы ( 42 He, 168 O, 40
20 Ca ). В рамках этой модели удалось объяснить устойчивость ядер и периодичность их свойств.
2.10.4. Дефект масс. Энергия связи атомного ядра.
Между частицами в ядре действуют ядерные силы (притяжения) и поэтому для того чтобы разделить ядро на составляющие его частицы необходимо
затратить некоторую энергию. Эта энергия получила название энергии связи
ядра.
Другими словами можно сказать, что энергия связи ядра равна энергии
выделяющейся при образовании ядра из отдельных частиц.
Поскольку закон ядерных сил не установлен, то рассчитать энергию связи
атомного ядра невозможно.
В результате точных измерений масс нуклонов и атомных ядер было
установлено, масса ядра всегда меньше, чем суммарная масса частиц, из которых она состоит. Иначе говоря, наблюдается дефект масс
m   Z  m p   A  Z  m n   m я .
10.3
На эту величину уменьшается масса всех нуклонов входящих в ядро. В
соответствии с формулой А.Эйнштейна E  mc2 можно подсчитать энергию
связи ядра
10.4
E  m  c2 .
На практике гораздо чаще используют не энергию связи, а удельную
энергию связи, т.е. энергию, приходящуюся на один нуклон ядра. На рисунке
показана зависимость удельной энергии связи от числа частиц в ядре. Из него
следует, что наиболее устойчивыми являются элементы средней части таблицы
элементов Менделеева. Тяжелые и легкие ядра менее устойчивы и, следовательно, энергетически выгодными являются процессы деления тяжелых ядер и
слияние легких.
3.10.4. Радиоактивное излучение и его состав.
В 1896 году Беккерель обнаружил, что соли урана самопроизвольно испускают излучение неизвестной природы, которое действует на фотопластинку,
ионизирует воздух, проникает через металлическую пластинку и вызывает свечение некоторых веществ (например, платиносинеродистого бария). Исследования Пьера и Марии Кюри было установлено, что подобное излучение свойственно не только урану, но и торию, и актинию. Несколько позже ими были
открыты новые химические элементы радий и полоний. Явление это получило
название радиоактивности, а излучение радиоактивным излучением.
Исследования было установлено, радиоактивные свойства не изменяются
при различных внешних воздействиях, а, следовательно, они обусловлены
структурой атомного ядра.
75
В настоящее время под радиоактивностью понимается способность некоторых ядер самопроизвольно превращаться в другие ядра с испусканием различных видов излучения и элементарных частиц. Различают естественную радиоактивность (неустойчивы ядра элементов существующих в природе) и искусственную (ядер атомов, полученных путем ядерных реакций и в природе не
существующих). Искусственная радиоактивность была обнаружена Ирен и
Фредериком Жолио-Кюри при бомбардировке  - частицами различных элементов (Нобелевская премия по физике за 1935 год).
Радиоактивное излучение имеет сложный состав. В магнитном поле оно
распадается на три компонента:
-  - излучение – слабо отклоняется магнитным полем, имеет положительный заряд и малую проникающую способность. Прямыми опытами (Резерфорд) было установлено, что это двукратно ионизированные атомы гелия.
-  - излучение – сильно отклоняется магнитным полем, обладает отрицательным зарядом. По отклонению в магнитном и электрическом полях был
определен удельный заряд частиц, который совпал со значением удельного заряда для электрона. Таким образом, было установлено, что  - излучение представляет собой поток быстро движущихся электронов.
-  - излучение – не отклоняется магнитным полем. Представляет собой
электромагнитное излучение, длина воны которого меньше, чем у рентгеновских лучей.
Теория радиоактивного распада строится на предположении о том, что
распад является спонтанным процессом и подчиняющимся статистическим законам. Случайный характер этого процесса позволяет сделать вывод о том,
число ядер N , распадающихся за время t , пропорционально числу ядер, т.е.
10.5
N    N  t ,
где  - постоянная распада, основная характеристика данного ядра. Знак
минус говорит о том, что общее число ядер в процессе распада уменьшается.
Разделив переменные и интегрируя, получим
dN
10.6
 dt  ln N  t  C .
N
Учитывая, что в начальный момент времени  t  0  число радиоактивных
ядер равно N 0 , то C  N 0 и тогда закон радиоактивного распада будет иметь
вид
N  N0et .
10.7
Определим время, в течение которого распадается половина из имеющихся ядер
N0
ln 2
.
10.8
 N 0et  2  eT  T 
2

Период полураспада основная характеристика радиоактивного элемента и
может принимать самые различные значения ( 4,5 млрд лет для урана до десятых и сотых долей секунды и меньше).
Радиоактивный распад происходит в соответствии с так называемые правилами смещения:
76
A
A 4
4
 - распад.
Z X  Z2Y  2 He ;
 - распад. AZ X  ZA1Y  01 e ;
в процессе  - излучения ядро переходит из возбужденного состояния в
основное и поэтому оно не испытывает превращений.
4.10.4.  - распад. Нейтрино.
Как мы уже указывали в процессе  - распада из ядра выбрасывается
электрон. При разработке теории  - распада пришлось преодолеть целый ряд
трудностей.
Одно из первых состояло в том, что электроны, выбрасываемые из ядра,
имеют непрерывный спектр, начиная от нуля до некоторого максимального
значения. Но как ядра, имеющие определенную энергию до и после распада,
могут выбрасывать электроны с различными значениями энергии.
Н.Бор даже попытался обосновать нарушение закона сохранения энергии в процессе
радиоактивного распада.
Вторая трудность состояла в том, что необходимо было обосновать происхождение электронов, выбрасываемых из ядра. Предположение о том, что
электрон вылетает из атома, не состоятельно, ибо при этом должно возникать
оптическое излучение, что не подтверждается экспериментально.
Третья трудность состояла в том, что в процессе  - распада не сохраняется спин. В процессе  - распада число нуклонов в ядре не меняется и естественh
но не должен изменяться и спин ядра. Но электрон имеет спин
и при вылете
2
электрона спин ядра должен измениться на эту величину, что не наблюдается
на опыте.
В 1931 году, чтобы разрешить указанные трудности, Паули выдвинул гипотезу, согласно которой одновременно с выбросом электрона из ядра выбраh
сывается еще одна частица – не имеющая заряда со спином равным
и реак2
ция  - распада имеет вид
A
A
0
0
10.9
Z X  Z1Y  1 e  0  .
Эту частицу Паули предложить назвать нейтрино (нейтрончик). Выдвинутая гипотеза позволила разработать стройную теорию  - распада. Экспериментально нейтрино было обнаружено лишь 26 лет спустя (1956 г.) в потоках
частиц возникающих при работе атомного реактора.
Нейтрино не имеет электрического заряда и массы покоя поэтому слабо
взаимодействует с веществом. Ионизирующая способность нейтрино столь мала, что один акт ионизации воздуха может произойти на пути в 500 км. Нейтрино не участвует в сильном взаимодействии и поэтому абсолютно свободно может пройти через 106 земных шаров поставленных друг на друга.
Поэтому экспериментальное обнаружение нейтрино представляло собой
довольно сложную экспериментальную задачу. Неслучайно, что Паули в пись77
ме к Дираку писал о том, что сегодня я ввел частицу, которую никто и никогда
не обнаружит.
Так как число нуклонов в ядре не меняется, то ответ на вопрос о происхождении электрона может быть лишь один. В ядре один из нейтронов превращается в протон по схеме
1
1
0
0
10.10
o n  1 p  1 e  0  .
Данная реакция возможна, так как масса покоя нейтрона больше массы
покоя протона.
Но если превращение испытывает нейтрон в атоме (связанный нейтрон),
то должен наблюдаться и распад свободных нейтронов. В 1950 году в потоках
нейтронов, возникающих в ядерных реакторах, было обнаружен радиоактивный
распад нейтронов, что и подтвердило данную теорию. Изучение нейтрино, приходящих на Землю из космоса, позволяет судить о процессах протекающих в
космосе. Для этого строят так называемые нейтринные телескопы, которые, как
правило, располагают глубоко под Землей.
5.10.4. Ядерные реакции и их основные типы.
Процесс превращения атомных ядер при взаимодействии с элементарными частицами или друг с другом называется ядерной реакцией.
В любой ядерной реакции выполняются основные законы (закон сохранения заряда, массового числа, импульса).
Важную роль в объяснении механизма ядерных реакций имело предположение Бора о том, что большинство ядерных реакций происходит в две стадии
10.11
Xa CYb.
На первом этапе образуется промежуточное ядро, которое является радиоактивным и на втором этапе оно испытывает распад. Например, первая реакция, наблюдаемая Резерфордом, протекает по схеме
14
4
18
17
1
10.12
7 N  2 He  9 F  8 O  1 H .
Наиболее интересными с этой точки зрения оказались реакции с участием
нейтронов. Для того, чтобы заряженная частица проникла в ядро она должна
иметь весьма большую энергию, так как она испытывает кулоновское отталкивание. И поэтому необходимо дорогостоящие ускорители заряженных частиц.
Нейтрон не имеет электрического заряда и поэтому не участвует в электромагнитном взаимодействии и поэтому может свободно проникать в ядро.
Более того, оказалось, что наиболее эффективными оказываются именно медленные нейтроны, так как они могут относительно долго находиться вблизи ядра.
Ядерные реакции с участием нейтронов не только сыграли огромную
роль в развитии физики, но и привели к появлению новых источников энергии.
При облучении нейтронами урана было установлено, что в уране образуются элементы средней части таблицы элементов Менделеева – барий и лантан.
Трудами многих ученых (Ферми, Ганн, Штрассман, Мейтнер, Курчатов,
78
Петржак и др.) было доказано, что появление этих элементов связано с делением ядер урана под действием медленных нейтронов.
Замечательной особенностью данной реакции является тот факт, что в
процессе деления ядер урана выделяется несколько (2 – 3) нейтрона, которые в
свою очередь могут вызвать деление других ядер. Это связано с тем, что осколки, образующиеся при делении, оказываются пересыщенными нейтронами и
выбрасывают их.
Наличие нейтронов, образующихся в процессе деления, приводит к тому,
что реакция деления может поддерживать сама себя и поэтому называется цепной реакцией деления.
Протекание цепной реакции определяется коэффициентом размножения
нейтронов, который определяется как отношение числа нейтронов до деления к
числу нейтронов после деления.
На величину коэффициента размножения влияет ряд факторов:
- деление ядер урана, приводит к увеличению коэффициента размножения;
- захват нейтронов 238
92 U без деления:
- вылет нейтронов за пределы вещества, приводит к тому, что цепная реакция деления может возникнуть только в том случае, если масса урана превышает некоторую критическую массу;
- захват нейтронов продуктами деления.
При значениях k  1 реакция идет в управляемом режиме, при k  1 происходит взрыв.
Впервые управляемая цепная реакция была осуществлена в США в 1942
году (Э.Ферми), а в СССР в 1946 году (И.В.Курчатов).
При делении одного ядра урана выделяется энергия порядка 200 МэВ.
Поэтому управляемая цепная реакция используется для получения электроэнергии.
Любопытно, что еще в 1956 году Н.Бор предупреждал, что мир погибнет не от атомной войны, а от мирного применения атомной энергии.
В настоящее время особое внимание уделяется реакторам размножителям
(бридерам) в которых при сжигании 235
92 U вырабатывается вторичное топливо,
по следующей схеме. При поглощении быстрого нейтрона ядро 238
92 U испытывает превращение
238
1
239
10.13
92 U  0 n  92 U .
Ядро 239
92 U (не существующее в природе) испытывает  - распад по схеме
239
239
0
10.14
92 U  93 Np  1 e .
Ядро 239
93 Np также радиоактивно и распадается по схеме
239
239
0
10.15
93 Np  94 Pu  1 e .
239
94 Pu имеет сравнительно большой период полураспада (24000 лет) и
может делиться под действием медленных нейтронов. При сжигании 1 кг 235
92 U
можно получить до 1,5 кг плутония.
79
Неиссякаемым источником энергии может стать реакция синтеза атомных
ядер – термоядерные реакции. Поскольку ядра имеют положительный заряд, то
испытывают кулоновское отталкивание. Для того, чтобы два ядра сблизились
на расстояние на котором начинают действовать ядерные силы (1015 м ) они
должны двигаться с огромной скоростью, поэтому эти реакции могут идти
только при огромных температурах 107 K  и называются термоядерными реакциями. Примеры таких реакций
2
2
3
1
1 H  1 H  2 He  1 H  4 МэВ
2
1
H  31 H  24 He  01 n  17,6 МэВ .
10.16
Li  21 H  24 He  24 He  22,4 Мэв
Эти реакции обладают тем свойством, что в них энергия, выделяющаяся
на одну частицу гораздо больше, чем в реакции деления (3,5 Мэв против 0,9
Мэв при делении). Особенностью данных реакций является и отсутствие радиоактивных отходов, которые в огромных количествах образуются в атомных
реакторах.
В настоящее время термоядерные реакции могут осуществляться только в
неуправляемом режиме (водородная бомба).
6
3
80