1.11 С.Н. Карамбиров.

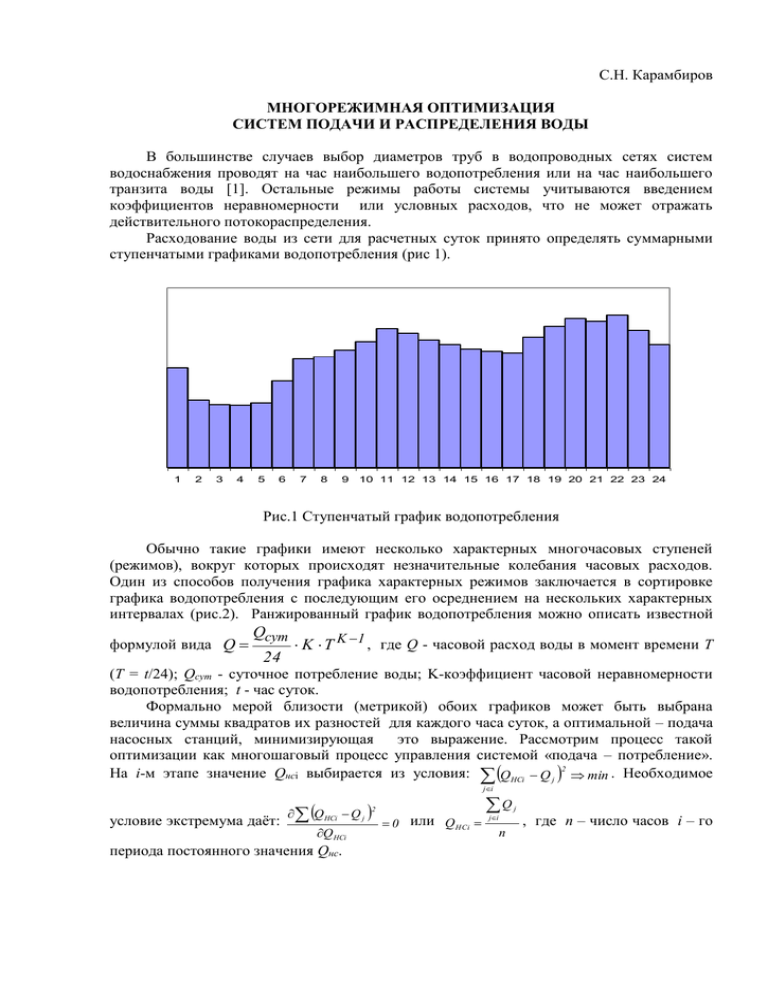
С.Н. Карамбиров
МНОГОРЕЖИМНАЯ ОПТИМИЗАЦИЯ
СИСТЕМ ПОДАЧИ И РАСПРЕДЕЛЕНИЯ ВОДЫ
В большинстве случаев выбор диаметров труб в водопроводных сетях систем
водоснабжения проводят на час наибольшего водопотребления или на час наибольшего
транзита воды [1]. Остальные режимы работы системы учитываются введением
коэффициентов неравномерности или условных расходов, что не может отражать
действительного потокораспределения.
Расходование воды из сети для расчетных суток принято определять суммарными
ступенчатыми графиками водопотребления (рис 1).
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Рис.1 Ступенчатый график водопотребления
Обычно такие графики имеют несколько характерных многочасовых ступеней
(режимов), вокруг которых происходят незначительные колебания часовых расходов.
Один из способов получения графика характерных режимов заключается в сортировке
графика водопотребления с последующим его осреднением на нескольких характерных
интервалах (рис.2). Ранжированный график водопотребления можно описать известной
формулой вида Q 
Qсут
24
 K  T K 1 , где Q - часовой расход воды в момент времени T
(T = t/24); Qcут - суточное потребление воды; K-коэффициент часовой неравномерности
водопотребления; t - час суток.
Формально мерой близости (метрикой) обоих графиков может быть выбрана
величина суммы квадратов их разностей для каждого часа суток, а оптимальной – подача
насосных станций, минимизирующая
это выражение. Рассмотрим процесс такой
оптимизации как многошаговый процесс управления системой «подача – потребление».
На i-м этапе значение Qнсi выбирается из условия:  QНCi  Q j 2  min . Необходимое
ji
условие экстремума даёт:
  Q НCi  Q j 
2
Q HCi
периода постоянного значения Qнс.
 0 или Q НCi 
Q
ji
n
j
, где n – число часов i – го
Рис.2. Упорядоченный график и характерные режимы
Таким образом, оптимальным значением Qнс на заданном отрезке является
усредненное на этом отрезке водопотребление. Легко показать, что это условие должно
выполняться для каждого шага, а процесс оптимизации сводится к выбору времени
переключения, где график водопотребления усредняется на некотором периоде. Задача
решается методом динамического программирования
[ Q( S ,U )  f k 1( S ' )],
f k ( S )  min
U
(1)
где S - состояние системы (ступень графика); U - управление (ширина интервала – час);
Q(S,U) - значение целевой функции (суммы квадратов разностей) при U-м варианте
управления на k-м шаге; S’ – состояние системы за k-1 ступеней до конца графика;
fk(S) - сумма квадратов разностей при оптимальном управлении за k ступеней до конца
графика для S-го варианта состояния. Расчет начинается с последней ступени. Для
обеспечения минимального объема регулирующих емкостей предусмотрена дальнейшая
оптимизация. График четырехступенчатого приближения неранжированного графика
водопотребления приведен на рис. 3.
Полученный график с меньшим числом ступеней является основой многорежимной
оптимизации.
Расчет базируется на методе линейного программирования [2] с
представлением каждого участка в виде телескопической трубы с рядом допустимых для
него стандартных диаметров подучастков (рис.4).
В работе предлагается выбирать параметры системы, обеспечивающие ее
оптимальное функционирование не для отдельно выбранного часа, а на всех характерных
режимах в целом с учетом величины требуемых подач и их продолжительности. В основу
расчета положен метод линейного программирования с представлением каждого участка в
виде телескопической трубы с рядом допустимых для него стандартных диаметров
подучастков (рис.4).
Рис.3. Приближение графика водопотребления
i
Xi1
Xi3
Xi2
li
Рис. 4. Телескопическая структура участков труб:
для i-го участка оптимизируются длины его подучастков xij
Очевидно, длина участка складывается из длин его подучастков, что задает первое
ограничение
ni
 X ij  li .
(2)
hij  Aij X ij ,
(3)
j 1
Потери напора на j-м подучастке
где Aij –потери напора на единицу длины трубопровода с расходом qi.
Гидравлические ограничения 2 закона Кирхгофа для кольца M, внешней увязки
напоров i-го и j-го водопитателей, а также ограничения обеспечения у потребителей
напоров не ниже требуемых, а у водопитателей - не выше допустимых, записываются для
каждого режима ti :
ni
ti
  Aij x ij   ;
(3)
i  M j 1
ni
( H вiti  Z вi )  ( H вjti  Z вj )    Aijti xij   ;
(4)
i1 j 1
H
ti

u
H
ti

вi
ni
  Atiij xij  Z вi  Z u  H требu ;
(5)
iI j 1
ti
H вi  H допi
(6)
где
ti
H вi  H допi - напоры (м), соответственно, у u-го узла и связанного с ним вi-го
водопитателя для режима ti; Zu, Zвi – аналогичные отметки, м; 1-путь (номера участков),
соединяющий узел u с водопитателем; Hтребu - требуемый напор u-го узла, м; Hдопiпредельный допустимый напор у вi-го водопитателя, м;  - точность увязки. Для
существующих участков (при реконструкции), соответствующий член суммы переносится
в правую часть ограничения.
Целевой функцией являются интегральные дисконтированные затраты на
строительство и эксплуатацию системы
Z
Tp
(
t 0
K t  C t ),
t
t
( 1 E ) ( 1 E )
(7)
где Кt – капиталовложения на t-м интервале времени; Ct - текущие затраты на t-м
интервале, за исключением капиталовложений;
E - норма дисконта (требуемая
инвестором норма доходности на единицу авансированного капитала);
Tp продолжительность расчетного периода. Величина интервала расчетного периода принята
равной 1 году.
Приводя затраты к началу строительства (t = 0) и считая продолжительность
строительства равной одному году, окончательно получим
1
1
(
1 E
1 E
Z  K 0  C 1(
1
1
1 E
Tp  1
)
 1 ),
(8)
n ni
где
K 0    cij xij , сij - стоимость единицы длины подучастка j-го диаметра, руб/м.
i 1 j 1
Стоимости насосных станций для рассматриваемых вариантов принимаются
постоянными. C1 - ежегодные эксплуатационные затраты (средние за расчетный период)
ni
Kв Q ti t перi e
H вiti ,
C 1   Pi  cij xij    вi
i 1
j 1
ti i 1 102 вi
n
(9)
где Pi- амортизационные отчисления для i-го участка; e - стоимость 1 квтч
электроэнергии, руб;
tперi - длительность периода ti в году, ч; вi – коэффициент
полезного действия насосных установок водопитателя вi; Kв- число насосных станций с
подачами Qtiвi (л/c) в период ti.
В экономический функционал, кроме затрат на строительство сетей, входят
суммарные затраты на электроэнергию по периодам. При этом, для насосных станций с
каждым режимом связана своя величина оптимального напора Htiвi, что на практике
сводится к изменению числа работающих насосов или к их регулированию.
Минимизация функционала Z с ограничениями (2)-(6) составляют задачу линейного
программирования. После ее решения оптимальные параметры становятся начальными,
проводится увязка сети для всех характерных режимов и расчет повторяется до их
совпадения. Аналогично учитываются сезонные и годовые колебания водопотребления.
На рисунке 5 показана многоэтапная сходимость процесса.
Рис.5. Типичная сходимость оптимизационного процесса
Выводы
Автором разработан метод приближения суточного графика водопотребления
ступенчатым графиком с меньшим числом ступеней и на его основе рассмотрена
многорежимная оптимизация, при которой ограничения формируются для каждого
режима водопотребления, а целевая функция обеспечивает минимум интегральных
дисконтированных затрат для всех режимов с учетом их продолжительности и процесса
управления.
Библиографический список
1. Абрамов Н.Н., Поспелова М.М., Сомов М.А. и др. Расчет водопроводных сетей:
Учебное пособие для вузов. М.: Стройиздат, 1983. 278 с.
2. Кикачейшвили Г.Е. Расчет оптимальных параметров систем подачи и распределения
воды. Тбилиси. Сабчота Сапартвело, 1980. 199 с.