L15-2

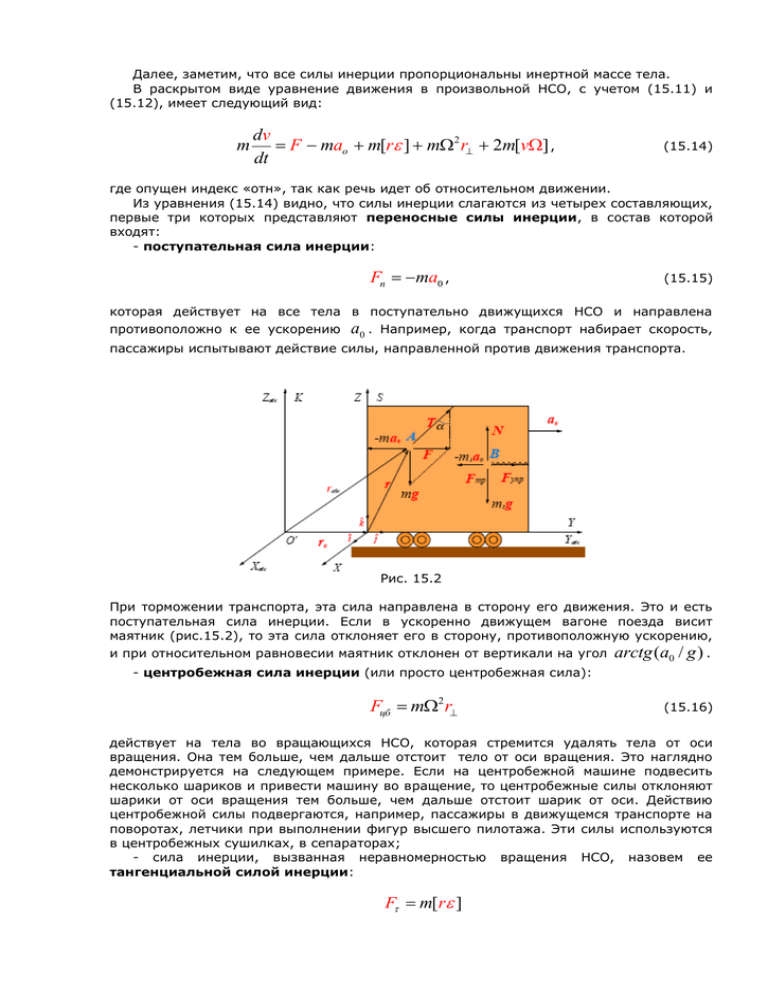
Далее, заметим, что все силы инерции пропорциональны инертной массе тела.
В раскрытом виде уравнение движения в произвольной НСО, с учетом (15.11) и
(15.12), имеет следующий вид:
m
dv
 F  mao  m[r ]  m2 r  2m[v] ,
dt
(15.14)
где опущен индекс «отн», так как речь идет об относительном движении.
Из уравнения (15.14) видно, что силы инерции слагаются из четырех составляющих,
первые три которых представляют переносные силы инерции, в состав которой
входят:
- поступательная сила инерции:
Fп  ma0 ,
(15.15)
которая действует на все тела в поступательно движущихся НСО и направлена
противоположно к ее ускорению
a0 .
Например, когда транспорт набирает скорость,
пассажиры испытывают действие силы, направленной против движения транспорта.
Рис. 15.2
При торможении транспорта, эта сила направлена в сторону его движения. Это и есть
поступательная сила инерции. Если в ускоренно движущем вагоне поезда висит
маятник (рис.15.2), то эта сила отклоняет его в сторону, противоположную ускорению,
и при относительном равновесии маятник отклонен от вертикали на угол
arctg (a0 / g ) .
- центробежная сила инерции (или просто центробежная сила):
Fцб  m2 r
(15.16)
действует на тела во вращающихся НСО, которая стремится удалять тела от оси
вращения. Она тем больше, чем дальше отстоит тело от оси вращения. Это наглядно
демонстрируется на следующем примере. Если на центробежной машине подвесить
несколько шариков и привести машину во вращение, то центробежные силы отклоняют
шарики от оси вращения тем больше, чем дальше отстоит шарик от оси. Действию
центробежной силы подвергаются, например, пассажиры в движущемся транспорте на
поворотах, летчики при выполнении фигур высшего пилотажа. Эти силы используются
в центробежных сушилках, в сепараторах;
- сила инерции, вызванная неравномерностью вращения НСО, назовем ее
тангенциальной силой инерции:
F  m[r ]
Четвертая – кориолисова сила инерции (или просто кориолисова сила)
Fkop  m[v]
(15.17)
которая действует перпендикулярно к относительной скорости тела, движущегося
во вращающейся СО, и поэтому искривляет его траекторию. Очевидно, эта сила
является гироскопической и не совершает работу. Если тело покоится во вращающейся
НСО, то на него Кориолисов сила не действует. Оно лишь подвергается действия
центробежной силы. Как тело начнет двигаться (в отличном от  направлении), оно
будет подвергаться еще и действия кориолисовой силы. Вот почему удержаться в
транспорте на поворотах легче в неподвижном положении, чем при движении.
Рис. 15.3
Действие силы Кориолиса можно демонстрировать на вращающемся вокруг
вертикальной оси диске, покрытой белой бумагой. Если погрузить шар в чернило, а
затем, положив на центр диска сообщить скорость v в горизонтальном направлении,
заметим, что хотя относительно лаборатории шар перемещается к краю диска
прямолинейно, на бумагу он оставляет кривой след (рис.15.3). Действительно, в СО,
связанной с лабораторией, на шар действуют силы тяжести и реакции опоры, которые
компенсируют друг друга, поэтому здесь движение прямолинейное. В СО, связанной с
диском, на движущий шар действует также кориолисова сила 2mvΩ, направленная
перпендикулярно скорости шара, в плоскости диска, которая и искривляет траекторию
шара относительно диска.
Система отсчета, связанная с Землей, как НСО.
Как известно, связанная с Солнцем СО (Гелиоцентрическая СО) является
инерциальной. Земля обращается вокруг Солнца с ускорением поступательного
а и совершает
  2 / 24  3600 рад / с вокруг
движения
суточное
своей
оси.
вращение
Так
что
с
угловой
связанная
с
скоростью
Землей
СО
(Геоцентрическая СО), является неинерциальной. Поместим начало координат в
центре Земли, а координатные оси жестко свяжем с Землей (рис.15.4).
Рис. 15.4
Так что в уравнении (15.14)
ао  а ,
a из-за практически равномерного вращения
Земли третий член в (15.14) равен нулю.
Ньютонов силу
F
представим в виде суммы трех сил:
F  F  F ,
где первая –
гравитационное притяжение Земли, второе - равнодействующая сил гравитационного
притяжения Солнца, Луны, планет и прочих небесных тел, третья – геометрическая
сумма всех остальных сил не гравитационного происхождения (сила сопротивления
воздуха, трения, натяжения нити, реакции опоры, электрических и магнитных полей и
прочие). Тогда уравнение (15.14) можно представить в виде:
ma  ( F  ma )  F  ( F  m2 r )  2m[v].
(15.18)
Воспользуемся обобщенным законом Галилея о том, что в малой области
гравитационного поля, независимо от их массы, все тела падают с одинаковым
ускорением. Это очевидным образом следует из того факта, что гравитационные силы,
как и силы инерции, строго пропорциональны массе тела. Так как размеры Земли очень
малы по сравнению с расстояниями Солнца, Луны и прочих небесных тел, то
создаваемое ими гравитационное поле в малой окрестности Земли можно считать
однородным. Поэтому в принятом приближении это поле частице А сообщает такое же
ускорение, что и центру Земли, т.е.
а .
Значит
F  ma ,
и первая скобка в правой
части уравнения (15.18) обращается в нуль. Итак, гравитационное действие всех
небесных тел, кроме Земли, полностью компенсируется поступательной силой инерции,
возникающей из-за ускорения, сообщаемой этими телами Земле. Именно этот факт (а
не малость!) является причиной того, что при рассмотрении движений тел околоземной
поверхности мы пренебрегаем действием Солнца, Луны и прочих небесных тел.
Рассмотрим теперь вторую скобку в (15.18). Учитывая, что гравитационное
притяжение Земли тоже пропорционально массе частицы А и выражается формулой
F  mg  ,
где
g -
ускорение свободного падения при отсутствии вращения Земли,
введем обозначение
F  m2 r  mg ,
где
g  g  2 r .
(15.19)
В окончательном виде уравнение относительного движения в Геоцентрической
системе отсчета будет
m
dv
 F  mg  2m[v].
dt
(15.20)
Рассмотрим сначала равновесие тела, лежащего на подставке, или подвешенного за
подвес. Так как при этом v =0, a =0, то из (15.20) находим F  mg . В первом случае
F
– реакция опоры
N , а во втором – натяжение нити T
рис. 15.5
(рис.15.5).
рис. 15.6
Введем определение: весом тела назовем приложенной к нему силе
что для P найдем
P  F . Так
P  mg .
Учитывая (15.19), видим, что вес тела состоит из двух слагаемых – гравитационного
притяжения Земли и центробежной силы инерции:
P  mg  m2 r .
(15.21)
Если тело подвешено на нити, то направление нити определяет направление силы
Р, следовательно и ускорения g. Оно называется направлением подвеса. Заметим,
что из-за центробежной силы это направление отличается от направления
если бы Земля была сферически симметричной. Действительно, при этом
g ,
g
даже
был бы
направлен к центру Земли, а направление отвеса на географической широте θ,
определяемое вектором g - отклоненной от направления к центру Земли на малый
угол (рис.15.6)
  sin    2 r / g  sin    2 R / g  cos sin  .
(15.22)
Этот угол обращается в нуль на полюсах и экваторе.
Реальная Земля (опять по причине вращения) слегка сплюснута вдоль оси
вращения, но и в этом случае формула (15.22) , хотя и приближенно, но является
достаточно точной. Проектируя векторы
g  и  2 r на направление вектора g , получим
g  g cos  2 r cos  g  2 R cos 2  ,
где
R -
радиус Земли. Точные измерения величины
983,2 см / с
2
вычислить и
на полюсе дают значение
978,0 см / с . Тогда по формуле (15.23) можно
  0 g  g  983,2 см / с2 , а на экваторе    / 2 
и на экваторе –
g  : на полюсе
g
(15.23)
2
g  g  2 R  981,2 см / с 2 . Очевидно, разность значений g  на полюсе и экваторе
обусловлена сплюснутостью Земли. Экватор дальше отстоит от центра Земли, чем
полюсы, поэтому тела на экваторе притягиваются к центру слабее, чем на полюсе.
Рис. 15.7 а
Рис. 15.7 б
Если тело движется относительно Земли, то в игру вступает и кориолисова сила
инерции, которая приводит к следующим эффектам (рис.15.7а). При движении по
меридиану к полюсам она смещает тела вправо по ходу их движения, т.е. на восток - в
северном полушарии, и на запад – в южном. Этим объясняется изношенность правых
берегов рек (Объ, Енисей, Лена), впадающих в Северный ледовитый океан. Заметьте,
при пересечении экватора по меридиану, сила Кориолиса меняет свой знак. Например,
пассаты – ветры, дующие по меридиану от тропиков к экватору от обоих полушарий,
под действием кориолисовой силы отклоняются к западу. При движении по параллелям
на восток (на запад) кориолисова сила действует на тело в сторону экватора
(соответствующего полюса) и вертикально вверх (вниз). Причем эти составляющие
силы Кориолиса зависят от географической широты: чем ближе параллель к экватору,
тем больше вертикальная сила. В частности, при движении по экватору сила Кориолиса
направлена вертикально: вверх – при движении на восток, и вниз – при движении на
запад.