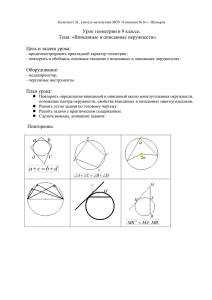
2.Многоугольник называется вписанным в окружность, если
реклама

Марафон. Тестовые задания. 1.Окружность называется вписанной в многоугольник, если: а) она касается всех вершин многоугольника; б) она касается сторон многоугольника; в) вершины многоугольника лежат на окружности; г) она касается всех сторон многоугольника. 2.Многоугольник называется вписанным в окружность, если: а) стороны многоугольника лежит на окружность; б) вершины многоугольника лежат на окружности; в) все вершины лежат на окружности; г) нет правильного ответа. 3.Свойство четырехугольника, в который можно вписать окружность: а) если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в этот четырехугольник можно вписать окружность; б) если около четырехугольника описана окружность, то суммы градусных мер его противоположных углов равны 180 градусов; в) если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны; г) если в четырехугольник можно вписать окружность, то суммы градусных мер его противоположных углов равны. 4.Условие, при котором около четырехугольника можно описать окружность: а) если в четырехугольнике суммы градусных мер противолежащих углов равны 180 градусов, то около такого четырехугольника можно описать окружность; б) если около четырехугольника описана окружность , то суммы градусных мер его противоположных углов равны; в) если в четырехугольнике сумм градусных мер противолежащих углов равны , то около такого четырехугольника можно описать окружность. г) нет правильного ответа. 5.Выберите неверные утверждения: а) в равностороннем треугольнике центр вписанной и центр описанной окружности совпадают; б) центр вписанной в треугольник окружности находится в точке пересечения биссектрис данного треугольника; в) в треугольнике центр описанной окружности находится в точке пересечения медиан треугольника; г) центр описанной окружности находится в точке пересечения серединных перпендикуляров; д) в прямоугольном треугольнике центр описанной окружности находится в точке, являющейся серединой гипотенузы; е) в равнобедренном треугольнике центры вписанной и описанной окружностей находятся на высоте, проведенной к основанию; ж) если в прямоугольник вписана окружность ,то ее центр находится в точке пересечения диагоналей. Задания на знание формул. 1. Какой формулой связаны радиус вписанной окружности в равносторонний треугольник с радиусом описанной окружности? ( r и R) 2. Запишите формулу для вычисления площади равностороннего треугольника , зная, что сторона треугольника равна а. ( S и a) 3. Как можно выразить радиус описанной около прямоугольного треугольника окружности через гипотенузу? (R и c) 4. Запишите формулу для вычисления площади треугольника через полупериметр и радиус вписанной окружности. (S p и r) 5. В трапецию вписана окружность. Какой формулой связаны радиус этой окружности с высотой этой трапеции. (r и h) Задачи на готовых чертежах. Просто задача 1. В ромб вписана окружность радиуса √3 см. Диагональ ромба равна его стороне. Найдите периметр ромба. Сложные задачи. 1. Около окружности описана равнобедренная трапеция, диагональ которой перпендикулярна боковой стороне. Радиус окружности равен 5см, меньшее основание равно 6 см. Найдите площадь трапеции. 2. Около равнобедренного треугольника с основанием 48 см описана окружность радиуса 25 см. В этот же треугольник вписана окружность . Найдите расстояние между центром вписанной и центром описанной окружностей.