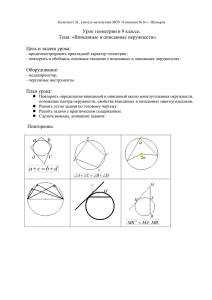
Окружность 1) СР-секущая СЕ-касательная

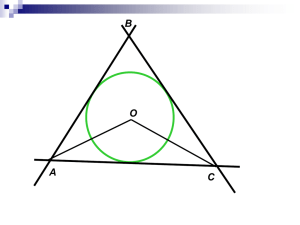
Окружность
1) СР-секущая СЕ-касательная
2) Диаметр перпендикулярный
хорде, делит ее пополам. Если
диаметр делит хорду пополам, то
он перпендикулярен ей.
3). КЕ*АЕ = ВЕ*СЕ = R2 –ОЕ2
1).Радиус, проведенный в точку касания, перпендикулярен касательной.
2). Если из некоторой точки плоскости проведено две касательных, то отрезки
касательных от этой точки до точек касания равны.
3) для любых секущих, выходящих из одной точки, к окружности выполняется
условие: ВЕ*АЕ=ЕС*ЕД=d2—R2
4). Для касательной и секущей, выходящих из одной точки, выполняется
условие: КР*КД=КМ2
1) вписанный—равен половине дуги
2) центральный – равен дуге
3) Величины всех вписанных углов, опирающихся на одну и ту же дугу
равны .
4) АМД= (дуга АД+ дуга СВ)/2 5) Угол АМД= (дуга АД― дуга ВС)/2
6)Угол, опирающийся на диаметр— прямой
Описанная: центр описанной окружности находится на пересечении
серединных перпендикуляров к сторонам
многоугольника.
R= (а*в*с)/4S. 2R = a/sinα = b/sinβ = c/sinγ
Если около четырехугольника можно описать окружность, то суммы его
противолежащих углов равны 180.
Если окружность описана около трапеции, то она равнобедренная.
Если окружность описана около прямоугольного треугольника, то ее
центр это середина гипотенузы, а радиус равен половине гипотенузы.
Если окружность описана около равнобедренного треугольника, то ее
центр лежит на высоте, проведенной к основанию.
Вписанная : центр находится на пересечении биссектрис углов
многоугольника.
Если в четырехугольник можно вписать окружность, то суммы его
противоположных сторон одинаковы.
Для любого многоугольника, в который вписана окружность. S = p* r
Если окружность вписана в прямоугольный треугольник, то r = (a+b-c)/2
Центр вписанной в равнобедренный треугольник окружности лежит на
высоте к основанию
Центры вписанной и описанной окружности в правильные
многоугольники совпадают.
3
4
6
а= R√3
а = R√2
а= R
R =2 r
a= 2r
r= (R√3)/2