УДК621.365.22 АНАЛИЗ ГАРМОНИЧЕСКОГО СОСТАВА ТОКОВ

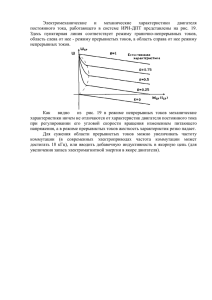
УДК621.365.22
АНАЛИЗ ГАРМОНИЧЕСКОГО СОСТАВА ТОКОВ ТРЕХФАЗНОЙ
ЭЛЕКРИЧЕСКОЙ ЦЕПИ С ДУГОЙ
Елизаров В.А., Елизаров К.А.
Россия, г. Москва, Национальный исследовательский университет «МЭИ»
Проводится анализ причин возникновения высших гармонических составляющих
токовв цепи с электрической дугой.Рассматривается влияние на величинувысших
гармонических составляющих токови спектральный состав параметров электрической
цепи. Исследованияоснованынаразработанноймоделитрехфазнойцеписдугой.
In the paper is carried out the analysis of the reasons of emergence of the high harmonic
components of current inthree-phase circuit with electric arc. Itis considered theinfluence of
parameters of electric circuit on currentsharmonic components value andit’s spectral structure.
The studies were based on developed model of three-phase circuit with the arc.
Электротехнологические установки с дугой получили широкое распространение
в современной технике, поскольку они используются для целого спектра задач – от
плавки черных и цветных металлов и сплавов на их основе, до восстановления руд и
получения сложных ферросплавов, огнеупоров и прочих химических соединений.
Основным источником нагрева в таких установках является электрическая дуга,
которая характеризуется существенной нелинейностью, вызывающей протекание в
питающей цепи несинусоидальных токов.
Подавляющее большинство электротехнологических установок с дугой, в силу
больших мощностей, питаются от трехфазных сетей переменного тока. При
совместном горении трех дуг происходит сильное искажение токов, возникает широкий
спектр гармонических составляющих, которые трансформируются в первичную
обмотку питающего трансформатора и передаются в энергосистему. Высшие
гармонические составляющие токов оказывают негативное влияние на силовое
оборудование, системы релейной защиты, автоматики и телекоммуникации.
Экономический ущерб, причиняемый воздействием высших гармоник, обусловлен
ухудшением энергетических показателей и сокращением срока службы
электрооборудования, общим снижением надежности электрических сетей. Для
уменьшения влияния на питающую сеть на стороне высокого напряжения печного
трансформатора устанавливают специальные фильтро-компенсирующие устройства,
которые предназначены для снижения
искажений тока и напряжения до
допустимых
в
энергосистемах
пределов. Основным недостатком
такого рода устройств являются
значительная стоимость и большие
габариты. Для успешной компенсации
высших
гармонических
составляющих токов необходимо
определить причины их появления и
их спектральный состав.
Рис. 1. Схема замещения трехфазной
Исследование гармонического
установки с дугой
состава
на
действующих
установках,как правило, затруднено, поэтому такое исследование целесообразно
провести на математической модели, позволяющей с достаточной точностью учесть все
особенности работы установки.
В основу разработанной модели леглаизвестнаясхема замещения силовой цепи
трехфазной дуговой печи (рис. 1), учитывающая активные и реактивные сопротивления
токоподводов и взаимные индуктивности фаз[1]. В исследуемой схеме первичная
сторона печного трансформатора приводилась к вторичной.На рис 1. обозначены:
– переменные ЭДС трансформатора для фаз A, Bи C;
–
собственные индуктивности фаз (индуктивности короткой сети и печного
трансформатора);
– суммарные активные сопротивления токоподвода и
трансформатора;
– активные сопротивления электродов;
–
нелинейные сопротивления дуг, зависящие от тока и длины дуги;
–
активные сопротивления расплава;
– взаимные индуктивности фаз;
– токи фаз.
Для схемы рис. 1 по методу контурных токов записывалась система уравнений
электрического равновесия для мгновенных значений во временной плоскости, которая
при помощи преобразований Лапласа представлялась в операторной форме, где
– полные нелинейные активные сопротивления фаз:
Решение нелинейной системы уравнений (1)осуществлялось методами
структурного моделирования в пакете прикладных программ MatlabSimulink.
Построенная структурная схема в терминах, принятых в Simulink, приведена на рис. 2.
13
16
23
24
5
4
7
17
Gain4
1
[Ua]
V_Ph_ARa
[Uda]
M1
20
Derivative5
du/dt
[Ia]
18
1
[Ra]
[Ia]
[Ia]
Ma.s
2
Phase A
Gain5
[Ub]
Cur_Ph_A
M2
Cur_Ph_B6
[Uda]
Ra
From6
Subsystem
V_Ph_B
Product
du/dt
[Udb]
Phase B
[Uc]
[Ic]
Gain6
M3
V_Ph_C
Derivative2
Cur_Ph_C
Gain3
M4
[Udc] Rc
Transfer Fcn4
Derivative4
Ib
From7
[Ic]
Ic
[Ib]
From
10
21
From1
8
[Ic]
11
From2
[Ib]
[Ua]
22
Product1 Cur_Ph_B2
[Rc]
From3
Cur_Ph_B4
[Udc]
From4
Rc
12
[Ub]
[Uc]
From8
Cur_Ph_B
Cur_Ph_B5
[Udb]
Rb
Subsystem1
Mb.s
Phase C
[Ib]
du/dt
1
Cur_Ph_B1
[Rb]
Rb
19
3
Transfer Fcn1
Derivative6
Ia
Subsystem2
Product2 Cur_Ph_B3
From5
[Ra]
du/dt
From9
14
15
25
6
9
[Rb]
From10
Рис. 2. Схема модели трехфазной дуговой печи в пакете структурного моделирования [Rc]
Matlab Simulink
From11
Приведенная на рис. 2 модель является имитационной и позволяет исследовать
влияниенесимметрии питающего напряжения, индуктивностей и взаимных
индуктивностей фаз, а также сопротивлений дуг на гармонический состав кривых
фазных токов также как и на реальной установке.ЭДС трехфазного печного
трансформатора на рис. 2 представлены блоками формирования синусоидального
s
периодического сигнала 1, 2 и 3, сдвинутыми на
относительно друг друга.
Нелинейные сопротивления фаз определялись в зависимости от протекающего в фазе
тока в блоках 4, 5 и 6. Напряжения дуги каждой фазы находились путем умножения
фазного тока на соответствующие сопротивления блоками 7, 8 и 9. Через блоки ввода
10, 11, 12 и блоки вывода 13, 14 и 15 напряжение на дуге передавались в модель.
Собственные и взаимные индуктивности фаз, а также их взаимодействие друг с другом
описывались совокупностью блоков 16. Проведение гармонического анализа
осуществлялось модулем быстрого преобразования Фурье. Для фиксации мгновенных
значений фазных токов и напряжений использовались виртуальные осциллографы,
данные в которые передавались при помощи блоков ввода 10 – 12 и 17 – 25.
Нелинейные сопротивления дуг представлялись в виде вольтамперных
характеристик, построенных по выражениям, которые приведены в [2].
Исследования проводились путем расчета переходных зависимостей тока и
вывода гистограмм постоянной составляющей, гармонических составляющих фазного
тока вплоть до тринадцатой по всем трем фазам печи для различных режимов работы, а
именно: при полной симметрии активных и индуктивных сопротивлений печного
контура, при несимметриии питающего напряжения, при несимметрии взаимных
индуктивностей, при несимметрии сопротивлений дуг, при несимметрии собственных
индуктивностей фаз.В качестве исходных данных для проведенияисследований
принимались параметры дуговой сталеплавильной печи емкостью 100 т ДСП-100Н3А.
Точность моделирования проверялась сравнительными расчетами с разными
значениями относительной погрешности и разными шагами дискретизации, а также
сопоставлением полученных данных с данными, приведенными в литературе[3].
Анализ полученных результатов позволяет связать несимметричность режимов
цепи с дугой с гармоническим составом кривой фазного тока. Было выявлено, что
появление четных гармонических составляющих в кривой тока в основном является
следствием погрешности вычисления. Величина третьей гармонической составляющей
связана в большей степени с несимметрии цепи в целом, а величина пятой гармоники –
отвечает процесса, происходящим в дуге. Нечетные гармоники более высоких порядков
практически не отражают режим работы цепи.
Результаты исследования могут быть использованы при подборе параметров
фильтро-компенсирующих устройств для цепей с дуговой нагрузкой.
Литература
1. Петелин Ю.Ю, Миронова А.Н., Запьянцев А.Н.Исследование электрических
параметров дуговой печи ДСП-25. // Исследование устройств электротермии:
Межвузовский сборник. Чебоксары: Изд. Чуваш.ун-та, 1985.С. 13-19.
2. GolkarM.A.,
TavakoliBinaM.,
MeschiS.
Anovelmethodofelectricalarcfurnacemodelingforflickerstudy.
//
Internationalconference on renewable energies and power quality 2007 (ICREPQ’07).
Sevilla, March 2007. – p. 222-230.
3. Расчет и измерение напряжения дуги ДСП. / В.А. Гордиенко, В.И. Дрогин, А.Н. Попов,
Н.А. Пирогов. // Математическое моделирование и расчет дуговых и плазменных
сталеплавильных печей. Сборник научных трудов ВНИИЭТО. М.: Энергоатомиздат, 1983.
С. 49-53.
Елизаров Владислав Александрович, аспирант кафедры ФЭМАЭК НИУ МЭИ,
111250, г. Москва, ул. Красноказарменная, д. 14, кафедра ФЭМАЭК. E-mail:
veliz@yandex.ru.
Елизаров Константин Александрович, к.т.н., ассистент кафедры ФЭМАЭК НИУ
МЭИ, 111250, г. Москва, ул. Красноказарменная, д. 14, кафедра ФЭМАЭК. E-mail
juko84@mail.ru.