исследование функции на монотонность элементарными
реклама

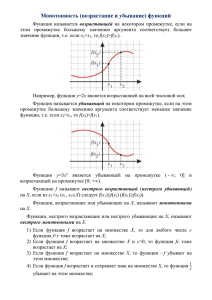
ИССЛЕДОВАНИЕ ФУНКЦИЙ НА МОНОТОННОСТЬ ПРИ РЕШЕНИИ УРАВНЕНИЙ И НЕРАВЕНСТВ Н.В. Худык ФГБОУ ВПО «Шадринский государственный педагогический институт», г. Шадринск Руководитель: к.п.н., доцент Чикунова О.И. Монотонность функции – одно из свойств, которым учащиеся должны уметь оперировать не только на наглядном и рабочем уровнях, согласно концепции А.Г. Мордковича, но и на формальном уровне (знать и уметь применять строгое определение возрастающей и убывающей функций) уже к окончанию основной школы. В практике обучения зачастую складывается так, что в 10-11 классах после знакомства с аппаратом дифференциального исчисления - признаками монотонности, они остаются единственным средством исследования функции на монотонность. Тем самым огромный потенциальный ресурс элементарного исследования функций на возрастание и убывание остается не реализованным. Мы считаем важным научить школьников применять для исследования функций на монотонность кроме определения и признаков ряд нижеперечисленных свойств. 1. Если f (x) возрастает (убывает) на множестве М и с - константа, то: а) функция f (x) + с возрастает (убывает) на М, б) функция с · f (x), с>0 возрастает (убывает) на М, в) функция с · f (x), с<0 убывает (возрастает) на М. 2. Если f (x) и g(x) возрастают (убывают) на множестве М, то: а) y= f (x)+ g(x) также возрастает (убывает) на М; б) y= f (x) g(x) также возрастает (убывает) на М , где f (x) и g(x) неотрицательны. 3. Если f (x) возрастает (убывает) на множестве М, то – f (x) убывает (возрастает) на М. 4. Если f (x) монотонна на множестве М и сохраняет постоянный знак, то функция 1 имеет противоположный характер монотонности на М. f x 5. Если f (x) и g(x) возрастают (убывают) на множестве М одновременно, то y f g x - возрастает на М. 6. Если f (x) и g(x) имеют разный характер монотонности на М, то y f g x – убывает. Приведем примеры исследования функций на монотонность с использованием перечисленных свойств. x1 2 2 1) Исследуем на монотонность и экстремумы: y 2 . Решение Функция является сложной y f g x . Пусть g x x 2 2 2; f 2 g . D y R , f 2 g на R. Найдем промежутки монотонности функции g и воспользуемся свойствами 5 и 6. g 0 7 6 5 4 3 2 1 1 2 3 4 5 6 7 1 7 6 5 4 3 2 1 x g f 1 2 3 4 5 6 7 x y f g x На промежутке ;1 y f g x . На промежутке 1; y f g x . x min 1 по определению. y min 1 1 . 4 Ответ: ;1 y f g x ; 1; y f g x ; y min 1 1 . 4 1 2) Исследуем на монотонность функцию: y x 1 . 6 x x 2 Решение y x 1 y1 1 2 x 12 6 14 x 10 , D y : 2 x x 6 0 y2 Преобразуем функцию. Введем обозначения и проанализируем монотонность функции на основе свойств на 3;-1 D y 3;-1 № cв-ва y1 5 y1 5 y2 3 y1 4 1 y2 y2 y2 3 2 3 № cв-ва 1 1 2 x 2 y y 1 1 y2 1 y2 Ответ: функция возрастает на 3;-1 . Приведем примеры, иллюстрирующие применение монотонности для решения уравнений, неравенств. 3) Решить уравнение x2 x 2 2 x 3 64 (*) Решение Очевидно, что x 0 не может являться решением уравнения (*), так как тогда x2 x 2 2 x 3 0 . Для x 0 функция y x2 x 2 2 x 3 непрерывна и строго возрастает 2 по свойству 2б). Значит, в области x 0 функция y x2 x 2 x3 принимает каждое свое значение ровно в одной точке. Ясно, что x 1 является решением уравнения (*), следовательно, это его единственное решение. Ответ: x 1 . 4) Решить неравенство 2 x 3 x 4 x 3 (**) Решение x Каждая из функций y 2 , y 3 x , y 4 x непрерывная и строго возрастающая на всей оси, значит по свойству 2а) исходная функция y 2 x 3 x 4 x является такой же. Легко видеть, что при x 0 функция y 2 x 3 x 4 x принимает значение 3, что не удовлетворяет условию задачи - 2 x 3 x 4 x 3 . В силу непрерывности и строгой монотонности этой функции при x 0 имеем 2 x 3 x 4 x 3 , что тоже не удовлетворяет условию. При x 0 имеем 2 x 3 x 4 x 3 . Следовательно, решениями неравенства (**) являются все x 0 . Ответ: x 0 . Для решения уравнений f g x f h x можно применять следующее свойство: если f x монотонна на X , то уравнение f g x f h x равносильно уравнению g x h x . 5) Решим уравнение 4 x 3 x 1 4 5 x 14 3 5 x 14 1 . Решение f g x f h x . Исследуем функцию Имеем уравнение вида монотонность. Пусть f x 4 x 3 x 1 , g x x , h x 5 x 14 . x 3 ïðè õ1 , Раскроем модуль, построим график f x 7 õ 3 ïðè õ1 Функция y f x возрастает на всей числовой прямой, следовательно, уравнение вида f g x f h x равносильно уравнению вида g x h x . Составим его: x 5 x 14 . Полученное уравнение равносильно системе x 0 , x 0 , ; 2 ; 2 x 5 x 14 x 5 x 14 0 x 7 . Ответ: 7. y f x на ó y x 3 4 1 0 1 x y 7 x 3 3 БИБЛИОГРАФИЯ 1. Бобровская, А.В., Чикунова, О.И. Практикум. Функции и графики: учеб.– метод. пособие для учащихся 9–11 классов. – Изд. 2-е./ А.В. Бобровская, О.И. Чикунова– Шадринск: Шадр. Дом Печати, 2012- 60 с. 2. Бобровская, А.В., Чикунова, О.И. Практикум. Уравнения. Неравенства. Системы: учеб.–метод. пособие для учащихся 8–11 классов. – Изд. 2-е./ А.В. Бобровская, О.И. Чикунова.– Шадринск: Шадр. Дом Печати, 2012- 76 с.