Задание 8
реклама
Задание 8
Аппроксимация. Линия эмпирической регрессии
~
Найдите аппроксимирующую формулу Y = f(X) для следующего двумерного множества точек:
Xi
2
4
6
8
10
Yi
5,5
6,3
7,2
8
8,6
1. Загрузите приложение MS Excel (Пуск Программы Microsoft Excel).
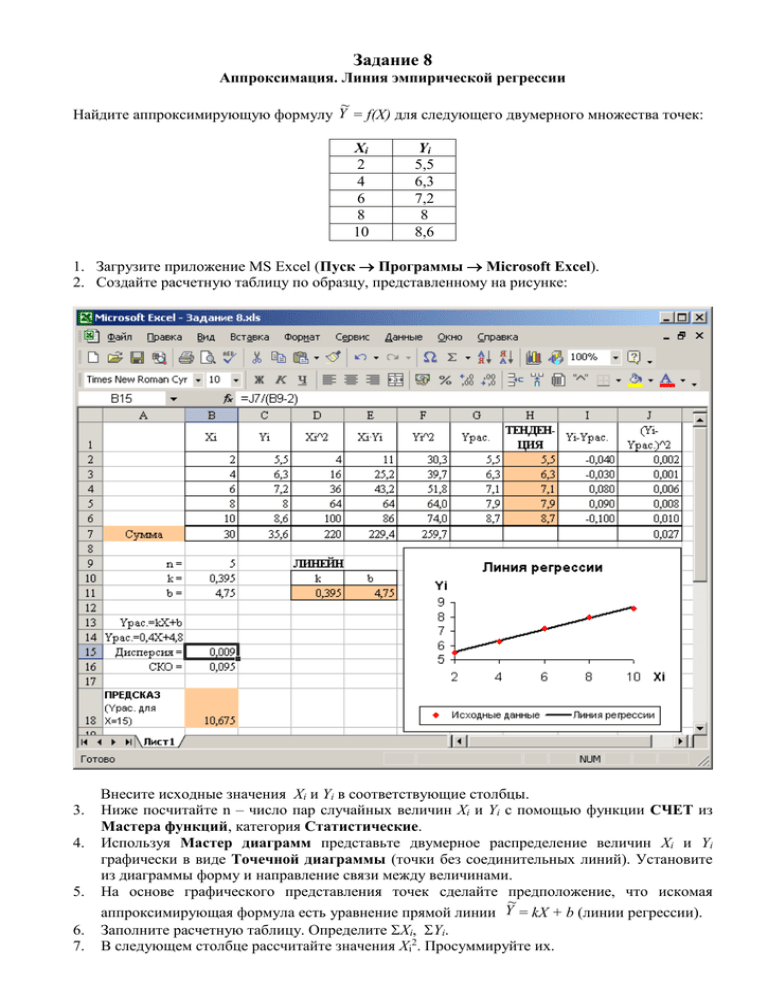
2. Создайте расчетную таблицу по образцу, представленному на рисунке:
3.
4.
5.
6.
7.
Внесите исходные значения Xi и Yi в соответствующие столбцы.
Ниже посчитайте n – число пар случайных величин Xi и Yi с помощью функции СЧЕТ из
Мастера функций, категория Статистические.
Используя Мастер диаграмм представьте двумерное распределение величин Xi и Yi
графически в виде Точечной диаграммы (точки без соединительных линий). Установите
из диаграммы форму и направление связи между величинами.
На основе графического представления точек сделайте предположение, что искомая
~
аппроксимирующая формула есть уравнение прямой линии Y = kX + b (линии регрессии).
Заполните расчетную таблицу. Определите Хi, Yi.
В следующем столбце рассчитайте значения Хi2. Просуммируйте их.
8.
9.
В следующем столбце рассчитайте значения Xi Yi. Просуммируйте их.
Определите коэффициенты линии регрессии по методу наименьших квадратов, используя
формулы
n X i Yi X i Yi
Yi k X i
b
,
k
2
2
n
n X i ( X i )
10. Рядом с рассчитанными по формулам значениями коэффициентов линии регрессии k и b
рассчитайте эти коэффициенты, используя функцию ЛИНЕЙН из Мастера функций,
категория Статистические.
Примечание 1: Функции, которые возвращают массивы, должны быть введены как формулы
массивов.
Создание формулы массива
При вводе формулы массива Microsoft Excel автоматически заключает ее в фигурные
скобки { }.
Если формула массива возвращает несколько значений, выделите диапазон ячеек, в
которые необходимо ввести формулу.
Наберите формулу.
Нажмите клавиши CTRL+SHIFT+ENTER.
Примечание 2: Функция ЛИНЕЙН возвращает массив из двух значений (коэффициенты k и b),
который описывает полученную с применением метода наименьших квадратов прямую линию,
которая наилучшим образом аппроксимирует имеющиеся данные известные_значения_x и
известные_значения_y. Поскольку возвращается массив значений, функция должна задаваться
в виде формулы массива (см. примечание выше). Для этого выделить в строке две стоящие
рядом ячейки, куда и будут помещены вычисленные значения коэффициентов.
11. Продолжите заполнение расчетной таблицы. В следующем столбце вычислите для каждого
~
значения Xi расчетное значение Yрас. ( Yi ), используя полученную аппроксимирующую
формулу.
12. Используя Мастер диаграмм, добавьте на уже построенную диаграмму исходных данных
Xi и Yi график линии регрессии, используя тип диаграммы Точечная, линия без маркеров.
~
13. В следующем столбце таблицы рассчитайте значения Yi , используя функцию
ТЕНДЕНЦИЯ из Мастера функций, категория Статистические.
~
14. Посчитайте отклонения расчетных значений Yi от исходных Yi.
15. Посчитайте квадраты отклонений. Просуммируйте их.
n
~
(Yi Yi ) 2
2 i 1
n2
16. Рассчитайте дисперсию
и среднее квадратичное отклонение σ.
Примечание 3: Функция ТЕНДЕНЦИЯ возвращает массив значений в соответствии с
линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов)
массивы известные_значения_y и известные_значения_x. Возвращает значения y, в
соответствии с этой прямой для заданного массива новые_значения_x (или если массив
новые_значения_x не задан, то для массива известные_значения_x).
~
17. Рассчитайте значения Yi , используя функцию ПРЕДСКАЗ из Мастера функций, категория
Статистические, для Х = 15.
Примечание 4: Функция ПРЕДСКАЗ вычисляет (или предсказывает) будущее значение y по
существующим данным известные_значения_x и известные_значения_y для любого
значения x.




