Лабораторная работа №3 нагреваемой воды в испарителе к кипящему фреону.
реклама
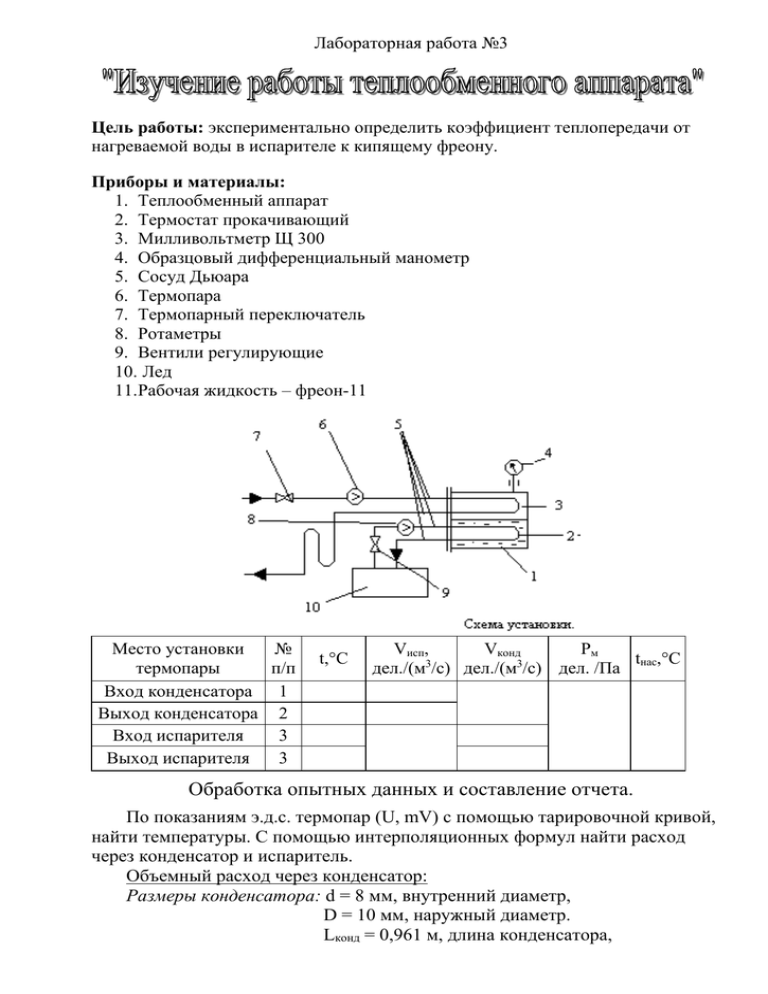
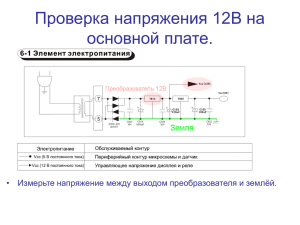
Лабораторная работа №3 Цель работы: экспериментально определить коэффициент теплопередачи от нагреваемой воды в испарителе к кипящему фреону. Приборы и материалы: 1. Теплообменный аппарат 2. Термостат прокачивающий 3. Милливольтметр Щ 300 4. Образцовый дифференциальный манометр 5. Сосуд Дьюара 6. Термопара 7. Термопарный переключатель 8. Ротаметры 9. Вентили регулирующие 10. Лед 11.Рабочая жидкость – фреон-11 Место установки № термопары п/п Вход конденсатора 1 Выход конденсатора 2 Вход испарителя 3 Выход испарителя 3 t,°C Vисп, Vконд Pм t ,°С 3 3 дел./(м /с) дел./(м /с) дел. /Па нас Обработка опытных данных и составление отчета. По показаниям э.д.с. термопар (U, mV) с помощью тарировочной кривой, найти температуры. С помощью интерполяционных формул найти расход через конденсатор и испаритель. Объемный расход через конденсатор: Размеры конденсатора: d = 8 мм, внутренний диаметр, D = 10 мм, наружный диаметр. Lконд = 0,961 м, длина конденсатора, а = 1,4·10-6 (м3/с)/дел.; в = 3,442·10-5 м3/с. Vконд(n) = a·n + в = Объемный расход воды через испаритель: Размеры испарителя: d 1 = 6мм = 6·10-3 м, внутренний диаметр, d2 = 8 мм, наружный диаметр, Lисп = 0,961 м, длина испарителя, a1 = 5,019·10-7 (м3/с)/дел.; BI = 2,49·10-6 м3/с. Vисп (n) = a1·n + в1= Образцовый дифференциальный манометр измеряет разность между давлением в камере и атмосферным давлением, поэтому необходимо сначала определить давление, измеренное манометром Рм, а затем добавить к нему атмосферное давление Ратм = 101325 Па. Давление насыщенных паров фреона 11 в корпусе теплообменного аппарата: Рм = Рнас = Рм + Ратм = Так как существует однозначная связь между температурой насыщенных паров и давлением жидкости, то температуру паров можно определить по давлению с помощью табличных данных зависимости Pнac = f (tнac). Общий тепловой поток, который передается от воды к фреону можно определить по формуле: Q = ·Vисп·Ср·(tвхода – tвыхода) = где р - плотность воды, ср - теплоемкость при постоянном давлении, tВХОД и tВЬ1ХОД -температура воды на входе и на выходе из испарителя. Коэффициент теплопередачи от воды к фреону -11: k Q F t ср F 2rL d 2 L 8 10 3 3.14 0.961 где F - площадь поверхности испарителя, tcp — среднелогарифмическая разность температур греющей и нагреваемой жидкости, в качестве нее используют среднюю логарифмическую разность температур: t ср t б t м t ln б t м где t6 = tвхода – tнac - больший и tм = tвыхода – tнac меньший температурные напоры между рабочими жидкостями. Если tб = tM = t б t м t ср Коэффициент теплоотдачи от воды к стенке испарителя он определить по формуле для турбулентного течения: Nu = 0.021 Re 0.8Рг0.43 где Nu = (d)/ - критерий Нуссельта; - коэффициент теплоотдачи, Вт/м К; d - внутренний диаметр трубки испарителя, м; - теплопроводность жидкости, Вт/м К; Re = (pud)/ - критерий Рейнольдса; р - плотность жидкости, кг/м3; uскорость течения жидкости, м/с; - динамическая вязкость жидкости, Па с; Рг = /а - критерий Прандтля, v - кинематическая вязкость жидкости, м /с; a- температуропроводность жидкости, м/с. Необходимые для расчета теплофизические свойства воды взять из табл. 2. u1 Vисп 4 d12 1 = 1 1 = 601.510 -6Пас Рг = 3,925. Re 1u1d1 1 Из критерия Нуссельта получим: 1 1 0.021 Re 0.8 Pr 0.43 d1 Оценить коэффициент теплоотдачи от стенки испарителя к кипящему фреону. Тепловой поток через единицу наружной поверхности трубы испарителя: q t ср Q d2 d d 1 F 2 ln 2 1d1 2 w d1 2 где d1, d2 - внутренний и наружный диаметры трубы; 1 - коэффициент теплоотдачи от воды к стенке трубы; 2 -коэффициент теплоотдачи от стенки трубы к фреону; w - коэффициент теплопроводности стенки испарителя (w =14 Вт/мК). Из последней формулы получим 2: 2 1 t ср F d 2 d d 2 ln 2 Q 1d1 2 w d1 Так же можно записать q = k2 Δtср, где k2 1 d 2 d 2 ln d 2 1 d 2 w d1 2 1 1 k2 – коэффициент теплопередачи отнесенный к наружной поверхности трубы и измеряется в Вт/м2К. В практических расчетах при d2/d1 2 коэффициент теплопередачи можно брать как для плоской стенки, погрешность расчета не превышает 4 %. Выводы: