Соотношение неопределённостей Гейзенберга

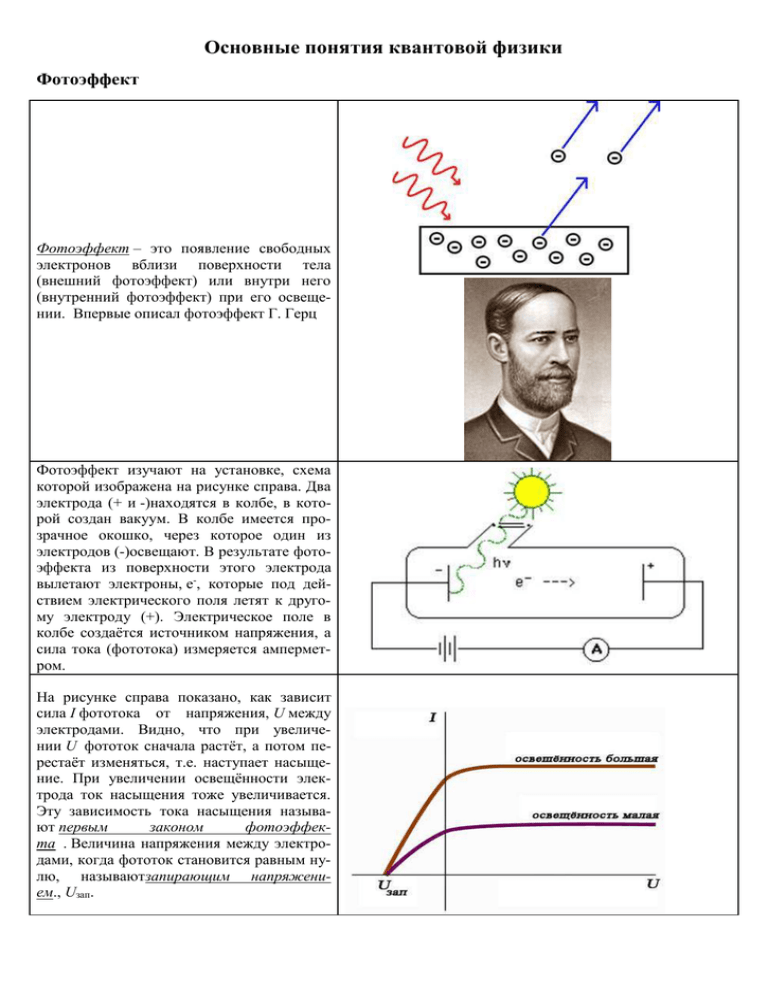
Основные понятия квантовой физики
Фотоэффект
Фотоэффект – это появление свободных
электронов вблизи поверхности тела
(внешний фотоэффект) или внутри него
(внутренний фотоэффект) при его освещении. Впервые описал фотоэффект Г. Герц
Фотоэффект изучают на установке, схема
которой изображена на рисунке справа. Два
электрода (+ и -)находятся в колбе, в которой создан вакуум. В колбе имеется прозрачное окошко, через которое один из
электродов (-)освещают. В результате фотоэффекта из поверхности этого электрода
вылетают электроны, е-, которые под действием электрического поля летят к другому электроду (+). Электрическое поле в
колбе создаётся источником напряжения, а
сила тока (фототока) измеряется амперметром.
На рисунке справа показано, как зависит
сила I фототока от напряжения, U между
электродами. Видно, что при увеличении U фототок сначала растёт, а потом перестаёт изменяться, т.е. наступает насыщение. При увеличении освещённости электрода ток насыщения тоже увеличивается.
Эту зависимость тока насыщения называют первым
законом
фотоэффекта . Величина напряжения между электродами, когда фототок становится равным нулю, называютзапирающим напряжением., Uзап.
При
запирающем
напряжении Uзап электрод, из которого вылетают
электроны, заряжен положительно и все
вылетевшие из него электроны возвращаются обратно (см. рис. справа). При этом
электрическое поле внутри колбы тормозит
фотоэлектроны и совершает работу, останавливая их. Поэтому справедливо следующее соотношение междуUзап и максимальное
кинетической
энергией Емаксфотоэлектронов:
, (1)
где е – заряд электрона. Таким образом, измеряя Uзап ,можно вычислить Емакс .
Второй закон фотоэффекта. Максимальная
кинетическая
энергия Емакс фотоэлектронов пропорциональна
частоте излучения и не зависит от интенсивности освещения электрода.
Третий закон фотоэффекта. Для каждого
материала (вещества) существует минимальная частота излучения, ниже которой
фотоэффект не наблюдается. Эта частота кр.гр.называется красной границей фотоэффекта,
Второй и третий законы фотоэффекта не могут быть объяснены в рамках классической физики, которую
мы изучали до сих пор. Для их объяснения А. Эйнштейн в 1905 использовал идею, высказанную ранее
немецким физиком М. Планком, согласно которой свет – поток частиц, фотонов. При этом энергия E каждого фотона, называемая квантом, равна:
E=h,
где - частота света, а h – коэффициент, названный постоянной Планка и равный 6,63.10-34 Дж.с.
Эйнштейн предположил, что фотон может выбить с поверхности только один электрон, а электрону,
чтобы вырваться из вещества, необходимо совершить работу выхода Авых. Тогда из закона сохранения
энергии следовало, что при фотоэффекте энергия фотона h должна быть равна сумме работы выхода Авых и кинетической энергии фотоэлектрона со скоростью v и массой m:
Уравнение (2), объясняющее все законы фотоэффекта, называют уравнением Эйнштейна для фотоэффекта. Таким образом, объяснить законы фотоэффекта можно только, если наделить электромагнитную волну свойствами частиц (т.е. корпускулярными свойствами) – фотонов, переносящих энергию в
виде квантов.
Эффект Комптона
Эффект Комптона – при рассеянии веществом
рентгеновского излучения наблюдается излучение с большей длиной волны. При этом длина
волны рассеянного излучения зависит от угла
рассеяния так, как это изображено на рисунке
справа. Видно, что фотон рентгеновского излучения с длиной волны i падает на электрон и отскакивает под углом  к направлению своего
первоначального движения. При этом электрон
под действием фотона тоже отскакивает, но в
другую сторону, как этого требует закон сохранения импульса и энергии. С помощью теории
относительности можно получить формулу, связывающую длину волны iпадающего и рассеянного f фотона, а также массу m0 электрона, постоянную Планка и скорость света.
Таким образом, частота рассеянного веществом
рентгеновского излучения не совпадает с частотой изучения, падающего на него. Это может
быть только, если электромагнитное излучение
представляет собой поток фотонов. При этом
часть энергии фотона уходит к электрону, а
остальную уносит рассеянный фотон. Поэтому
частота рассеянного фотона всегда меньше, чем
падающего. Эффект Комптона – ещё одно доказательство корпускулярной природы электромагнитного излучения.
На рисунках справа показаны зависимости энергии и длины волны ’ рассеянного фотона от угла, под которым он рассеялся. Видно, что чем
больше угол , тем меньшую энергию имеет рассеянный фотон. Соответственно, при увеличении  больше энергии приобретает электрон.
Атомы лёгких элементов с малым зарядовым
числом не поглощают рентгеновское излучение,
а только рассеивают его. Поэтому вещества, не
содержащие тяжёлых элементов (железо, кальций и т.п.), не отбрасывают тень в рентгеновских
лучах. Однако лёгкие элементы хорошо рассеивают рентгеновские лучи. Поэтому наркотики и
взрывчатку можно обнаружить, изучая рассеянное ими рентгеновское излучениедаже если они
находятся внутри металлических контейнеров.
Волновые свойства частиц
Было экспериментально показано, что пучок
электронов, пролетая через две параллельные
щели в экране, взаимодействуют друг с другом так, как когерентные лучи света, давая
интерференционную картину, аналогичную
той, которая была получена в опытах Юнга.
Это доказывает, что частицы ведут себя аналогично волнам. Эта гипотеза о корпускулярно-волновом дуализме была впервые высказана Луи де Бройлем в 1924 г. Таким образом, любые материальный объекты сочетают в себе волновые и корпускулярные
свойства. Согласно этому длина  волны любой частицы, обладающей импульсом p, равна
Таким образом, пучок электронов можно
рассматривать как волну, длину которой
можно сделать очень маленькой, т.е. меньше
длины волны видимого света, если придать
электронам достаточно большой импульс.Такие электронные волны можно использовать для изучения очень малых объектов, которые остаются невидимыми в обычных световых микроскопах. Поэтому изучение очень малых объектов проводят с помощью электронных микроскопов, один из которых показан на рисунке справа.
Соотношение неопределённостей Гейзенберга
Корпускулярно-волновой дуализм даёт возможность
заменить движущуюся частицу эквивалентной волной.
Сделав такую замену, мы лишаем частицу корпускулярных свойств, а значит, не можем определить её положение. Таким образом, корпускулярно-волновой дуализм не позволяет одновременно и точно измерить положение частицы и её импульс. Однако в этом случае
погрешности одновременного определения положения
частицы (x) вдоль оси хи проекции её импульса (p)
вдоль той же оси оказываются связанными между собой
с помощью соотношения
,
(1)
которое называют соотношением или принципом неопределённости Гейзенберга в честь немецкого физика
В.К. Гейзенберга, который в 1927 году впервые вывел
это соотношение. Согласно соотношению неопределённости произведение погрешностей в измерении положения и импульса частицы по порядку величины всегда
больше постоянной Планка. Из (1) следует, что невозможно точно указать одновременно координаты частицы и ее импульс. При этом, чем точнее определяют в
опыте одну из этих характеристик частицы, тем менее
точным будет значение другой. В результате, траектория движения такой частицы становится неопределённой.
Следует отметить, что соотношение неопределённости
Гейзенберга не может быть объяснено несовершенством
экспериментальной техники. Это соотношение - следствие корпускулярно-волнового дуализма, проявляющегося в микромире.
Корпускулярно-волновой дуализм накладывает определённые ограничения не только на погрешности в измерении координат и импульса частицы. Соотношение,
аналогичное (1), существует также для погрешностей в
измерении энергии (E) системы и времени (t), в течение которого это измерение сделано:
.
Соотношение неопределённостей можно вывести, если
описать дифракцию электрона с импульсом р на щели
шириной х .
Принцип неопределённости вытекает из эффекта Комптона, т.к. изучая электрон, мы обязательно должны передать ему часть энергии кванта фотона. В результате,
положение электрона и его импульс изменится.
Давление света
Согласно теории Максвелла электромагнитная
волна является поперечной волной. Когда такая
волна наталкивается на поверхность, например,
на металлическую, напряжённость электрического поля начинает двигать электроны вдоль
направления своего вектора (см. рисунок справа).
При этом отрицательно заряженные электроны
будут двигаться в сторону, противоположную
вектору Е. Легко показать, что на движущиеся в
магнитном поле волны электроны будет действовать сила Лоренца, направленная вглубь поверхности металла в направлении вектора скорости
распространения волны. Это и есть давление
электромагнитной волны или давление света.
Впервые давление света было измерено российским физиком П.Н. Лебедевым с помощью крутильных весов, схематически изображённых на
рисунке. В стеклянном сосуде, в котором создавали вакуум, на серебряной нити (Н) подвешивали тонкий стержень (С) с закрепленными на нём
белыми
и
чёрными
тонкими
дискамикрылышками (К) толщиной 0,1 – 0,01 мм и диаметром 5 мм, сделанными из металла или слюды.
Так как давление света на белые диски больше,
чем на чёрные, то крутильные весы поворачивались, и по их углу поворота можно было судить о
величине этого давления. Давление света в солнечный день составляет около 4.10-6 Па, что согласуется с величиной, которую можно вывести,
исходя из теории электромагнитного поля Максвелла.