1. Методические указания
реклама

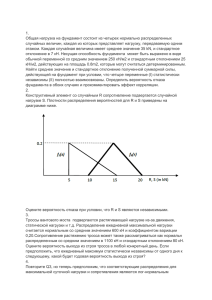
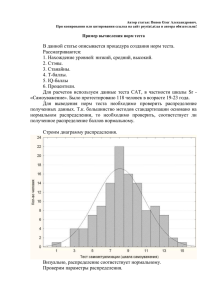
1 Методические указания по выполнению заданий самостоятельной работы. 1. Выполнение задания в программе EXCEL. Разместить все данные в одной колонке. Выполнить команды: «Сервис» - «Анализ данных» - «Описательная статистика» - «ОК». «Входной интервал» - выделить все ячейки набора данных (напр. $O$13:$O$53). «Выходной интервал» - указать ячейку, в которую будут выводиться данные (напр. $R$39) – любая свободная ячейка. «ОК». Полученные данные округлить до двух десятичных знаков. Построение гистограммы. «Сервис» - «Анализ данных» - «Гистограмма» - «Вывод графика» - «ОК». Гистограмма представляет собой графическое представление частот в наборе данных (гистограмма показывает, как часто встречается то или иное значение, отмеченное на горизонтальной оси). Гистограмма нормального распределения Нормальное распределение представляет собой «идеально» гладкую 68% σ гистограмму в форме колокола (колокол Гаусса), в которой большинство значений 2σ 95% сконцентрировано в средней части 3σ диапазона данных, а остальные значения с 99% затуханием симметрично расположены по обе стороны от вершины колокола. Распределение Гаусса http://www.youtube.com/watch?v=7NUGpzspLD4 http://www.youtube.com/watch?v=GANHXlMpVMc&feature=related Большинству социально-экономических явлений присущи свойства нормального распределения случайных величин. Проверка данных на соответствие нормальному распределению проводится в два этапа. Во-первых, визуально изучается «наличие колокола». Если он присутствует, то (вовторых) используя «Описательные статистики» рассмотреть, входит ли 68% значений в интервал +/- 1σ от среднего, 95% +/- 2σ и 99% +/- 3σ. Имеются ли значения, выходящие за интервал +/- 3σ? Если имеются значения, выходящие за пределы 99% диапазона, то они считаются «выбросами» и исключаются из дальнейшего рассмотрения, как нетипичные. 2. Для решения задачи рассчитывается средневзвешенное значение по формуле: X X i * i , где ω – удельный вес каждого наименования. В свою очередь, удельный вес рассчитывается: Xi X 3. Удельный вес и средняя цена рассчитываются аналогично, как в задании 2. _ PP, Отклонение от средней цены = рассчитывается: (X i размах = Pmax Pmin , стандартное отклонение X ) 2 * i , коэффициент вариации v *100% X Коэффициент вариации характеризует «однородность» имеющихся данных. Однородность Прогнозируемость Высокая Высокая 0 v 10% Средняя (нормальная) Средняя 10 v 30% Низкая Низкая v 30% 2 4. Для сравнения различных вариантов с вероятностями наступления событий используются среднее и стандартное отклонение, которые рассчитываются как средневзвешенные. Для этого используются формулы: Среднее µ = Е(Х) Е(Х)= Х * Р( Х ) ; Р(Х) – вероятность появления значения Х Стандартное отклонение ( Х ) 2 * Р( Х ) Среднее значение показывает ожидаемое значение (в данном случае прибыльность проекта) Х, ст. отклонение характеризует неопределенность наступления этого события (риск). 5. Расчет вероятности наступления события производится путем вычисления коэффициента Стьюдента (t) с последующим определением значения вероятности по таблице вероятностей для нормального распределения. Для суммы Для среднего sum n * Среднее Для доли X X sum n * X Стандарт. ошибка Sх S sum * n tСтьюдент t n S * (1 ) n X sum sum t S sum X Sx t S μ и π – значения, которые характеризуют генеральную совокупность. X и - значения по выборке, для которых вычисляется вероятность. Вычисление вероятностей производится по таблице 1: Расчет вероятности при помощи EXCEL. Мастер функций, НОРМРАСПР, подставляются значения (Х, µ, σ, истина), получаем результат. 6. Расчет экономически обоснованного объема выборки. Для решения задач по определению объема выборки необходимо воспользоваться одной из формул: Для среднего n - объем выборки Для доли признака n - объем выборки n t 2 * 2 2 σ – ст. отклонение t - коэффициент Стьюдента t 2 * * (1 ) n 2 Δ – предельная ошибка ρ - доля признака 90% 95% 99% t = 1,64 t = 1,96 t = 2,47 - среднеквадратическое или стандартное отклонение. Значение σ берется по результатам (а) предыдущих исследований, (б) пилотных исследований или (в) по усмотрению исследователя. В последнем случае, если стандартное отклонение не указано, то дисперсия 2 или * (1 ) принимается равной своему максимальному значению 0,25. 3 - точность исследования или предельная ошибка, задается при постановке задачи исследования. (долях, %, грн. и т.д.). и в формуле должны быть выражены в одинаковых единицах Таблица 1 Распределение вероятностей наступления события для нормального распределения (1. больше; 2. меньше; 3. вне диапазона; 4. внутри диапазона) 4 7. Построение доверительного интервала означает распространение (экстраполяцию) результатов по выборке на всю генеральную совокупность, т.е. формулирование статистического вывода. Для построения доверительного интервала используются формулы: Для X - t*SХ ≤ µ ≤ X + t*SХ SХ = среднего n Для доли признака ρ - t* Sр ≤ π ≤ ρ + t* Sр Sр = р(1 - р) n Так, разница значений среднего генеральной совокупности µ и среднего выборки Х равна предельной ошибке (t*SХ) или точности исследования ( ). Х - µ = t*SХ , или Х - µ = Δ = t*SХ, (SХ, Sр - стандартная ошибка) t 2 * 2 В свою очередь, SХ = , т.е. Δ = t* , отсюда n 2 n n 8. «Производить или закупать?», «Make or buy?» а). Сравнить затраты, связанные с изготовлением с затратами, связанными с приобретением. Использовать формулу точки безубыточности. б). Критерием приоритетности выступает рентабельность пролукции. (см. конспект). 9. Для решения задач по ценообразованию необходимо уметь рассчитать коэффициент эластичности, изменение объема продаж, размер прибыли, рентабельность продаж. (см. конспект). 10. Проверка гипотез. Построить доверительный интервал с уровнем достоверности 95%. Если тестируемое значение окажется «внутри» диапазона значений, значит предположение (гипотеза) не подтверждается. Если это значение находится «за пределами» доверительного интервала, значит, предположение подтверждается. 11. АВС-XYZ анализ. АВС – анализ заключается в распределении товарного ассортимента на группы (А, В, С) в соответствии с их удельным весом в общем товарообороте. Порядок выполнения: 1. Рассчитать удельный вес каждого наименования в общем товарообороте. 2. Расположить полученные значения по убыванию. 3. Нарастающим итогом сформировать группы А – 80%, В – 15%, С – 5% общего товарооборота. Рассмотреть особенности каждой группы, предложить мероприятия по управлению товарным ассортиментом. XYZ – анализ заключается в распределении товарного ассортимента по критерию стабильности спроса. Выполняется в том же поле, что и АВС – анализ. Порядок выполнения: 1. По имеющимся данным за предыдущий период рассчитывается среднее значение и стандартное отклонение спроса по каждому наименованию, рассчитывается коэффициент вариации спроса (задание 3). 2. Полученные значения располагаются в порядке возрастания. 3. Формируются группы: Характеристика спроса Прогнозируемость X устойчивый высокая 0 v 10% Y колеблющийся средняя 10 v 30% Z нестабильный низкая v 30% По результатам проведенного анализа составляется матрица АВС-XYZ анализа. А В С X АX BX CX Y AY BY CY Z AZ BZ CZ Лучшими позициями являются группы AX, AY, AZ.Слабые позиции CX,CY,CZ. 5 12. Предложить политику управления запасами означает рассчитать следующие показатели: текущий запас, страховой запас, средний запас, цикл заказа, точку заказа, оптимальный размер заказа, оборачиваемость запасов в соответствии с заданным уровнем обслуживания клиентов и сделать выводы.