Ф-10-1x

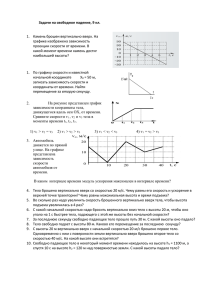
Горбанева Л.В.,
старший преподаватель
кафедры физики ДВГГУ
Основы кинематики
Кинематика является одной из основных частей механики. Основная
задача механики – определить положение тела в любой момент времени.
Кинематика
изучает
различные
механические
движения
тел
без
рассмотрения причин, вызывающих эти движения.
Любое движение происходит по закону, который должен определять
положение тела в пространстве в данный момент времени. Закон движения
должен давать зависимость координат x, y, z от времени. Для упрощения
расчетов часто тело принимают за материальную точку.
Положение материальной точки в пространстве в любой момент
времени (закон движения) можно определять либо с помощью зависимости
координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо
при помощи зависимости от времени
радиус-вектора
способ),
𝑟⃗ = 𝑟⃗(𝑡) (векторный
проведенного
из
начала
координат до данной точки (рис. 1). На
рисунке ⃗⃗⃗⃗
𝑟0 – радиус-вектор положения
точки в начальный момент времени,
𝑟⃗(𝑡) – радиус-вектор положения точки в момент времени t.
Тогда
перемещение
тела
–
вектор,
соединяющий
начальное
положение тела с его последующим положением – 𝑆⃗ = ∆𝑟⃗ = 𝑟⃗(𝑡) − ⃗⃗⃗⃗.
𝑟0
Значит, чтобы найти закон движения, надо вычислить проекции вектора
перемещения на оси координат.
В
случае
равномерного
движения
вдоль
оси
ОХ
проекция
перемещения тела на ось ОХ равна Sх=х – х0=Vxt и уравнение движения
примет вид: x=x0+Vxt., где x0 – координата тела (или точки) в начальный
момент времени, Vx – проекция вектора скорости тела на ось ОХ, t – время
движения тела.
Быстрота изменения положения материальной точки в пространстве с
течением времени характеризуется средней и мгновенной скоростями.
Средняя
скорость
–
векторная
величина,
равная
отношению
перемещения к промежутку времени, за которое это перемещение
⃗⃗ =
произошло: 𝑉
∆𝑆⃗
∆𝑡
.
В физике наибольший интерес представляет не средняя, а мгновенная
скорость, которая определяется как предел, к которому стремится средняя
скорость на бесконечно малом промежутке времени Δt:
⃗
𝑟⃗
∆𝑡
∆𝑡
⃗⃗ = ∆𝑆 =
𝑉
(∆𝑡 → 0).
В математике такой предел называют производной и обозначают
𝑑𝑟⃗
𝑑𝑡
или ⃗⃗⃗⃗
𝑟 ` (𝑡).
⃗⃗ тела в любой точке криволинейной
Мгновенная скорость 𝑉
траектории направлена по касательной к траектории в этой точке. При t→0
⃗⃗⃗⃗⃗
⃗⃗ .
𝑉ср → 𝑉
⃗⃗
При движении тела по криволинейной траектории его скорость 𝑉
изменяется
по
направлению.
Изменение
скорости
за
модулю
некоторый
и
вектора
малый
промежуток времени Δt можно задать
⃗⃗ (рис. 2).
с помощью вектора ∆𝑉
Вектор
изменения
скорости
⃗⃗ = ⃗⃗⃗⃗
∆𝑉
𝑉2 − ⃗⃗⃗⃗
𝑉1 за малое время Δt можно разложить на две составляющие:
⃗⃗⃗⃗𝜏 , направленную вдоль вектора 𝑉
⃗⃗ (касательная составляющая), и ∆𝑉
⃗⃗⃗⃗
∆𝑉
𝑛,
⃗⃗ (нормальная составляющая).
направленную перпендикулярно вектору 𝑉
⃗⃗ = ∆𝑉
⃗⃗⃗⃗𝜏 + ∆𝑉
⃗⃗⃗⃗
Изменение вектора скорости за время ∆t: ∆𝑉
𝑛
Мгновенным ускорением (или просто ускорением) 𝑎⃗ тела называют
⃗⃗ к малому промежутку
предел отношения малого изменения скорости ∆𝑉
времени Δt, в течение которого происходило изменение скорости:
𝑎⃗ =
⃗⃗
∆𝑉
∆𝑡
=
⃗⃗⃗⃗⃗𝜏
∆𝑉
∆𝑡
+
⃗⃗⃗⃗⃗
∆𝑉
𝑛
(∆t→0)
∆𝑡
Направление вектора ускорения 𝑎⃗ в случае криволинейного движения
не совпадает с направлением вектора
⃗⃗ .
скорости 𝑉
Составляющие вектора
ускорения 𝑎⃗ называют касательным
и нормальным
(тангенциальным) ⃗⃗⃗⃗⃗
𝑎𝜏
𝑎𝑛 ускорениями (рис. 3).
⃗⃗⃗⃗⃗
Касательное ускорение указывает, насколько быстро изменяется
скорость тела по модулю: ⃗⃗⃗⃗⃗
𝑎𝜏 =
⃗⃗
∆𝑉
∆𝑡
(∆t→0).
Вектор
𝑎𝜏 направлен по
⃗⃗⃗⃗⃗
касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела
изменяется по направлению.
Криволинейное
движение
можно представить как движение
по дугам окружностей (рис. 4).
Нормальное
ускорение
зависит от модуля скорости V и от
радиуса R окружности, по дуге которой тело движется в данный момент:
𝑎𝑛 =
𝑉2
𝑅
. Вектор ⃗⃗⃗⃗⃗
𝑎𝑛 всегда направлен к центру окружности.
Из рис. 3 видно, что модуль полного ускорения равен
𝑎 = √𝑎𝜏 2 + 𝑎𝑛 2 .
2
𝑎⃗⃗𝑡
Уравнения для описания равнопеременного движения: 𝑆⃗ = ⃗⃗⃗⃗
𝑉0 𝑡 + ,
2
⃗⃗ = ⃗⃗⃗⃗
𝑉
𝑉0 + 𝑎⃗t. Координата изменяется по следующей закономерности: 𝑥 =
𝑥0 + 𝑉0 𝑡 +
𝑎𝑡 2
2
.
Для свободного падения тел ускорение принимается равным 9,8м/с 2
или 10м/с2.
Графики равномерного и равнопеременного движения.
График зависимости перемещения от времени показан на рисунке 5.
Из графика видно, что скорость 𝑉 =
𝑆1
𝑡1
= 𝑡𝑔𝛼.
График зависимости скорости от
времени показан на рисунке 6. Из графика
видно,
что
перемещение
S1=V1
t1,
численно равно площади прямоугольника
ОАВС.
График зависимости скорости от времени показан на рисунке 7. Из
графика видно, что 𝑎 =
площади
0abc.
𝑉1 −𝑉0
График
𝑡1
= 𝑡𝑔𝛽, а перемещение S численно равно
зависимости
перемещения от времени при V0=0, имеет
вид, показанный на рисунке 8. Скорость
тела в данный момент времени t1 равна
тангенсу угла наклона между касательной
к графику и осью времени: V=tgα.
Рассмотрим примеры решения задач.
Пример 1. Поезд прошел первую половину пути со скоростью
V1=72км/ч, вторую половину пути – со скоростью 36 км/ч. Определите
среднюю скорость поезда.
Решение. Средняя скорость прохождения пути 𝑉 =
∆𝑆
∆𝑡
.
Время движения складывается из двух промежутков времени t1 –
времени, и t2, в течение которого поезд движется со скоростью V1 и равного
𝑆
2𝑉1
, и времени t2 – времени, в течение которого поезд движется со скоростью
V2 и равного
𝑆
2𝑉2
:
𝑡 = 𝑡1 + 𝑡2 =
𝑆
2𝑉1
Подставив численные значения 𝑉ср =
+
𝑆
2𝑉2
2∙10∙20
10+20
, откуда 𝑉ср =
𝑆
𝑆
𝑆
+
2𝑉1 2𝑉2
=
2𝑉1 𝑉2
𝑉1 +𝑉2
.
= 13,3м/с.
Пример 2. При равноускоренном движении из состояния покоя тело
проходит за пятую секунду 90см. Определить перемещение тела за седьмую
секунду.
Решение. Изобразим на рисунке 9
координаты тела.
Проведем ось в направлении движения
тела, а начало оси выберем в точке О, из которой тело начинает движение.
Тогда, согласно уравнению движения, 𝑥4 =
𝑎𝑡42
2
, 𝑥5 =
𝑎𝑡52
2
, где t4=4c, t5=5c.
Следовательно, перемещение тела за пятую секунду 𝑆5 = 𝑥5 − 𝑥4 =
Откуда 𝑎 =
2𝑆5
2
(𝑡5 −𝑡42 )
2
.
.
Аналогично, 𝑆7 = 𝑥7 − 𝑥6 =
уравнения 𝑎 =
𝑎(𝑡52 −𝑡42 )
2𝑆5
(𝑡52 −𝑡42 )
𝑎(𝑡72 −𝑡62 )
2
получим: 𝑆7 =
, где t7 =7c, t6=6c. С учетом
𝑆5 (𝑡72 −𝑡62 )
𝑡52 −𝑡42
.
Подставив численные значения, получаем S7=1,3м.
Пример 3. Тело брошено вверх с высоты ho = 2 м со скоростью 30
м/с. Определить
1)
время полета до падения на землю t .
2)
максимальную высоту подъема tmax;
3)
конечную скорость V ко н .
Решение.
В задаче рассматривается свободное падение тела, т.е.
движение под действием силы тяжести при отсутствии сопротивления, при
котором тело движется с постоянным ускорением g – ускорением
свободного падения, направленным вертикально вниз. Ось Y
направим вертикально
вверх. Начало
поместим на поверхности земли
отсчета
(рис.
координат
10).
Проекция
начальной скорости на O Y положительна: Voy=V0.
Проекция ускорения на OY отрицательна: ay= –g.
Тогда уравнение движения примет вид:
𝑦(𝑡) = ℎ0 + 𝑉0 𝑡 −
𝑔𝑡 2
2
, где y0=h0.
1) Когда тело упадет на землю, y(t) станет равным нулю. Из этого
условия можно определить время полета тела: 0= ℎ0 + 𝑉0 𝑡 −
Решая квадратное уравнение, получим: 𝑡1,2 =
Очевидно, t>0, поэтому выбираем 𝑡 =
𝑔𝑡 2
2
𝑉0 ±√𝑉02 +2𝑔ℎ0
𝑉0 +√𝑉02 +2𝑔ℎ0
𝑔
𝑔
.
.
.
Скорость при движении изменяется согласно формуле: Vy=V0y – gt.
В наивысшей точке аодъема скорость станет равной нулю:
0=V0 – gtпод.
Отсюда время подъема до наивысшей точки 𝑡под =
𝑉0𝑦
𝑔
.
2) Подставляя это выражение в уравнение движения
ℎ𝑚𝑎𝑥 = ℎ0 + 𝑉0 𝑡под −
2
𝑔𝑡под
2
, найдем максимальную высоту подъема
hmax:
ℎ𝑚𝑎𝑥
𝑉02 𝑔𝑉02
𝑉02
= ℎ0 +
− 2 = ℎ0 +
𝑔
2𝑔
2𝑔
Подставляя численные данные, получим: ℎ𝑚𝑎𝑥 = 2 +
900
2∙9,8
= 47,9м.
3) Для определения скорости тела в момент падения на землю
подставим найденное время полета в уравнение для скорости: Vкон=V0y – gt:
𝑉кон = 𝑉0 − 𝑔
𝑉0 +√𝑉02 +2𝑔ℎ0
𝑔
= −√𝑉02 + 2𝑔ℎ0 .
𝑉кон = −√900 + 2 ∙ 9,8 ∙ 2 = −30,6м/с.
Конечная скорость направлена вниз, поэтому ее проекция на ось OY
отрицательна, что и получено при решении задачи.
Пример 4. Одно тело брошено вертикально вверх с начальной
скоростью V0, другое свободно падает с высоты h. Найдите зависимость
расстояния между телами от времени, если известно, что тела начали
движение одновременно.
Решение. Направим ось OY вертикально верх, начало
оси выберем на поверхности земли (рис. 11). Так как тела
брошены одновременно, то время их движения одинаково и
законы движения имеют вид 𝑦1 = 𝑉01 𝑡 −
𝑔𝑡 2
2
, 𝑦2 = 𝑦0 −
𝑔𝑡 2
2
,
где 𝑦0 – начальная координата второго тела.
Расстояние между телами в любой момент, пока одно из
тел не упадет, выражается уравнением
𝑔𝑡 2
𝑔𝑡 2
∆𝑦 = 𝑦2 − 𝑦1 = 𝑦0 −
− 𝑉01 𝑡 +
= 𝑦0 − 𝑉01 𝑡
2
2
или
∆𝑦 = ℎ − 𝑉01 𝑡.
Задачи для самостоятельного решения.
10.1.1. Тело падает с высоты h0 и при ударе теряет 20% своей скорости.
Определить максимальную высоту, на которую поднимается тело после
удара.
10.1.2. Тело падает вертикально вниз с высоты 20м без начальной скорости.
Определить путь h, пройденный телом за последнюю секунду падения.
10.1.3. С башни высотой h0 одновременно бросают два шарика: один вверх
со скоростью V01, другой вниз со скоростью V02. Определить зависимость
расстояния между шариками от времени.
10.1.4. Два пункта А и В расположены на расстоянии l=240м друг от друга
на склоне горы. От пункта А начинает равноускорено спускаться к пункту В
велосипедист с начальной скоростью V01=8м/с. Одновременно из пункта В к
пункту А начинает равнозамедленно подниматься мотоциклист с начальной
скоростью V02=16м/с.
Они встречаются через t1=10с, к этому времени
велосипедист проехал S1=130м. С каким ускорением ехал каждый из них?
10.1.5. С поверхности земли с одинаковыми скоростями V0=20м/с вверх
последовательно через промежуток времени ∆t=1с брошены два мяча.
Определить, когда и на каком расстоянии от поверхности земли они
встретятся. Считать g=10м/с2.
10.1.6. Мяч брошен вертикально вверх. На высоте h он побывал дважды с
интервалом времени ∆t. Определить начальную скорость бросания мяча.
10.1.7. Мяч, брошенный вертикально вверх, упал на землю через 3с. С какой
скоростью был брошен мяч и на какую высоту он поднялся?
10.1.8. Тело бросают вертикально вверх со скоростью 4,9м/с. Одновременно
с предельной высоты, которой оно может достичь, бросают вертикально
вниз другое тело с той же начальной скоростью. Определить время, по
истечении которого тела встретятся.
10.1.9. Автомобиль проходит первую треть пути со скоростью V1, а
оставшуюся часть пути со скоростью V2 = 50 км/ч. Определить скорость
автомобиля (км/ч) на первом участке, если средняя скорость на всем
пути Vcp = 37,5 км/ч.
10.1.10. При равноускоренном движении тело проходит за первые равные
последовательные промежутки времени, по t = 4 с каждый, пути S1 = 24 м
и S2 = 64м. Определить ускорение и начальную скорость тела.
10.1.11. Тело движется прямолинейно с постоянным ускорением и в шестую
секунду проходит 12м. Определите ускорение и путь, пройденный в
шестнадцатую секунду, если начальная скорость была равна нулю.
10.1.12. Сколько времени и с какой высоты падало тело, если за последние
2с оно прошло 60м ?